华师大版八年级上册14.1.3反证法 课件(共26张PPT)
文档属性
| 名称 | 华师大版八年级上册14.1.3反证法 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 09:50:08 | ||
图片预览






文档简介
(共26张PPT)
路边苦李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李.
王戎是怎样知道李子是苦的呢 他运用了怎样的推理方法
这与事实矛盾。说明李子是甜的这个假设是错的还是对的?
假设李子不是苦的,即李子是甜的,
那么这长在人来人往的大路边的李子会不会被过路人摘去解渴呢?
那么,树上的李子还会这么多吗?
所以,李子是苦的
一、问题情境
小华睡觉前,地上是干的,早晨起来,看见地上全湿了。小华对婷婷说:“昨天晚上下雨了。”
你能对小华的判断说出理由吗?
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
小华的理由:
我们可以把这种说理方法应用到数学问题上。
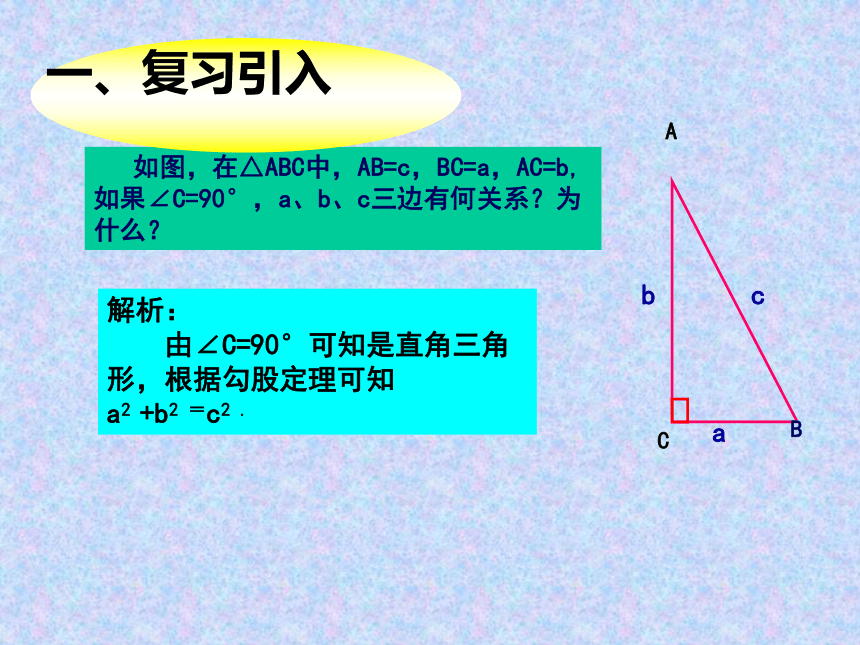
解析:
由∠C=90°可知是直角三角形,根据勾股定理可知
a2 +b2 =c2 .
如图,在△ABC中,AB=c,BC=a,AC=b,如果∠C=90°,a、b、c三边有何关系?为什么?
A
C
B
a
b
c
一、复习引入
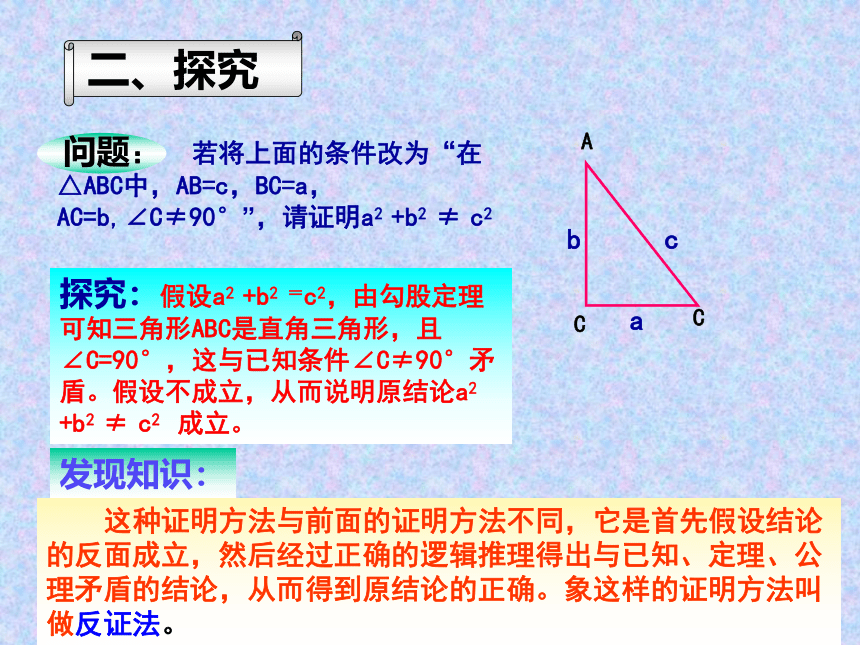
探究:假设a2 +b2 =c2,由勾股定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
A
C
C
若将上面的条件改为“在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请证明a2 +b2 ≠ c2
a
b
c
这种证明方法与前面的证明方法不同,它是首先假设结论的反面成立,然后经过正确的逻辑推理得出与已知、定理、公理矛盾的结论,从而得到原结论的正确。象这样的证明方法叫做反证法。
问题:
发现知识:
二、探究
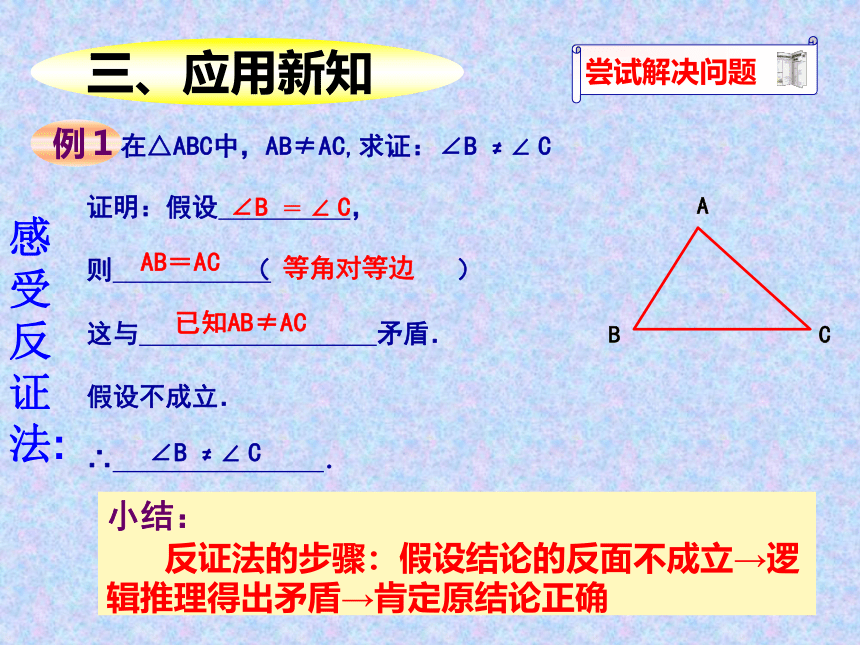
三、应用新知
在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
A
B
C
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
已知AB≠AC
∠B ≠ ∠ C
小结:
反证法的步骤:假设结论的反面不成立→逻辑推理得出矛盾→肯定原结论正确
例1
尝试解决问题
感受反证法:
证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
例2
求证:两条直线相交只有一个交点。
已知:如图两条相交直线a、b。
求证:a与b只有一个交点。
a
b
A
●
A,
●
A
证明:假设a与b不平行,则可设它们相交于点A。
那么过点A 就有两条直线a、b与直线c平行,这与“过直线外一点有且只有一条直线与已知直线平行矛盾,假设不成立。
∴a//b.
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
已知:如图有a、b、c三条直线,且a//c,b//c.
求证:a//b
a
b
c
例3
求证:在一个三角形中,至少有一个内角小于或等于60°。
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
点拨:至少的反面是没有!
例4
∠A+∠B+∠C>60°+60°+60°=180°
例6、用反证法证明:等腰三角形的底角必定是锐角.
分析:解题的关键是反证法的第一步否定结论,需要分类讨论.
已知:在△ABC中,AB=AC.
求证:∠B、∠C为锐角.
证明:假设等腰三角形的底角不是锐角,那么只有两种情况:
(1)两个底角都是直角;
(2)两个底角都是钝角;
反证法的一般步骤:
假设命题结论不成立
假设不成立
假设命题结论反面成立
与已知条件矛盾
假设
推理得出的结论
与定理,定义,公理矛盾
所证命题成立
什么时候运用反证法呢?
证明真命题 的方法
直接证法
间接证法
反证法
美国总统华盛顿从小非常聪明,小偷翻进鲍克家偷走了许多东西,根据迹象表明小偷就是本村人,华盛顿灵机一动,对全村人讲起了故事:“黄蜂是上帝的使者,能辨别人间的真假.”忽然华盛顿大声喊道:“小偷就是他,黄蜂正在他的帽子上兜圈子,要落下来了!”大家回头张望,看着那个想把帽子上的黄蜂赶走的人,其实哪有什么黄蜂?华盛顿大喝一声:“小偷就是他!”
你知道华盛顿是如何推理的吗?
华盛顿抓小偷
万事开头难,让我们走好第一步!
写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥b
a<0
b是0或负数
a不垂直于b
a∥b
1.在一个梯形中,如果同一条底边上的两个内角不相等,那么这个梯形是等腰梯形吗?请证明你的猜想.
谁来试一试!
2.已知:如图△ABC中,D、E两 点分别在AB和AC上
求证:CD、BE不能互相平分
(平行四边形对边平行)
做一做
学习是件很愉快的事
证明:假设CD、BE互相平分
连结DE,故四边形BCED是平行四边形
∴BD∥CE
这与BD、CE交于点A矛盾
假设错误, ∴CD、BE不能互相平分
四、巩固新知
1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
已知:在梯形ABCD中,AB//CD,
∠C≠∠D
求证:梯形ABCD不是等腰梯形.
证明:假设梯形ABCD是等腰梯形。
∴∠C=∠D(等腰梯形同一底上的两内角相等)
这与已知条件∠C≠∠D矛盾, 假设不成立。
∴梯形ABCD不是等腰梯形.
4、求证:如果一个梯形同一底上的两个内角不相等,那么这个梯形不是等腰梯形。
A
B
C
D
五、拓展应用
1、已知:如图,在△ABC中,AB=AC,∠APB≠∠APC。
求证:PB≠PC
A
B
C
P
证明:假设PB=PC。
在△ABP与△ACP中
AB=AC(已知)
AP=AP(公共边)
PB=PC(已知)
∴△ABP≌△ACP(S.S.S)
∴∠APB=∠APC(全等三角形对应边相等)
这与已知条件∠APB≠∠APC矛盾,假设不成立.
∴PB≠PC
美国总统华盛顿从小非常聪明,小偷翻进鲍克家偷走了许多东西,根据迹象表明小偷就是本村人,华盛顿灵机一动,对全村人讲起了故事:“黄蜂是上帝的使者,能辨别人间的真假.”忽然华盛顿大声喊道:“小偷就是他,黄蜂正在他的帽子上兜圈子,要落下来了!”大家回头张望,看着那个想把帽子上的黄蜂赶走的人,其实哪有什么黄蜂?华盛顿大喝一声:“小偷就是他!”
你知道华盛顿是如何推理的吗?
华盛顿抓小偷
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
六、全课总结
1、知识小结:
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论
2、难点提示:
利用反证法证明命题时,一定要准确而全面的找出命题结论的反面。至少的反面是没有,最多的反面是不止。
大家议一议!
通过本节内容的学习,你们觉得哪些题型宜用反证法 ?
我来告诉你(经验之谈)
(1)以否定性判断作为结论的命题;
(2)以“至多”、“至少”或“不多于”等形式陈述的命题;
(3)关于“唯一性”结论的命题;
(4)一些不等量命题的证明;
(5)有些基本定理或某一知识体系的初始阶段等等.(如平行线的传递性的证明)
注意:用反证法证题时,应注意的事项 :
(1)周密考察原命题结论的否定事项,防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说明命题的真伪性;
(3)在推理过程中,要充分使用已知条件,否则推不出矛盾,或者不能断定推出的结果是错误的。
课时作业设计
用反证法证明下列命题:
1.求证:三角形内角中至多有一个内角是钝角。
2.已知:如图,AB∥CD,AB ∥EF。
求证:CD ∥EF。
3.求证:圆内两条不是直径的弦不能互相平分。
4.证明“在同一平面内,垂直于同一条直线的两条直线互相平行.”
A
B
C
D
E
F
第2题图
路边苦李
王戎7岁时,与小伙伴们外出游玩,看到路边的李树上结满了果子.小伙伴们纷纷去摘取果子,只有王戎站在原地不动.
王戎回答说:“树在道边而多子,此必苦李.”
小伙伴摘取一个尝了一下果然是苦李.
王戎是怎样知道李子是苦的呢 他运用了怎样的推理方法
这与事实矛盾。说明李子是甜的这个假设是错的还是对的?
假设李子不是苦的,即李子是甜的,
那么这长在人来人往的大路边的李子会不会被过路人摘去解渴呢?
那么,树上的李子还会这么多吗?
所以,李子是苦的
一、问题情境
小华睡觉前,地上是干的,早晨起来,看见地上全湿了。小华对婷婷说:“昨天晚上下雨了。”
你能对小华的判断说出理由吗?
假设昨天晚上没有下雨,那么地上应是干的,这与早晨地上全湿了相矛盾,所以说昨晚下雨是正确的。
小华的理由:
我们可以把这种说理方法应用到数学问题上。
解析:
由∠C=90°可知是直角三角形,根据勾股定理可知
a2 +b2 =c2 .
如图,在△ABC中,AB=c,BC=a,AC=b,如果∠C=90°,a、b、c三边有何关系?为什么?
A
C
B
a
b
c
一、复习引入
探究:假设a2 +b2 =c2,由勾股定理可知三角形ABC是直角三角形,且∠C=90°,这与已知条件∠C≠90°矛盾。假设不成立,从而说明原结论a2 +b2 ≠ c2 成立。
A
C
C
若将上面的条件改为“在△ABC中,AB=c,BC=a, AC=b,∠C≠90°”,请证明a2 +b2 ≠ c2
a
b
c
这种证明方法与前面的证明方法不同,它是首先假设结论的反面成立,然后经过正确的逻辑推理得出与已知、定理、公理矛盾的结论,从而得到原结论的正确。象这样的证明方法叫做反证法。
问题:
发现知识:
二、探究
三、应用新知
在△ABC中,AB≠AC,求证:∠B ≠ ∠ C
A
B
C
证明:假设 ,
则 ( )
这与 矛盾.
假设不成立.
∴ .
∠B = ∠ C
AB=AC
等角对等边
已知AB≠AC
∠B ≠ ∠ C
小结:
反证法的步骤:假设结论的反面不成立→逻辑推理得出矛盾→肯定原结论正确
例1
尝试解决问题
感受反证法:
证明:假设a与b不止一个交点,不妨假设有两个交点A和A’。
因为两点确定一条直线,即经过点A和A’的直线有且只有一条,这与与已知两条直线矛盾,假设不成立。
所以两条直线相交只有一个交点。
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
例2
求证:两条直线相交只有一个交点。
已知:如图两条相交直线a、b。
求证:a与b只有一个交点。
a
b
A
●
A,
●
A
证明:假设a与b不平行,则可设它们相交于点A。
那么过点A 就有两条直线a、b与直线c平行,这与“过直线外一点有且只有一条直线与已知直线平行矛盾,假设不成立。
∴a//b.
小结:根据假设推出结论除了可以与已知条件矛盾以外,还可以与我们学过的定理、公理矛盾
已知:如图有a、b、c三条直线,且a//c,b//c.
求证:a//b
a
b
c
例3
求证:在一个三角形中,至少有一个内角小于或等于60°。
已知:△ABC
求证:△ABC中至少有一个内角小于或等于60°.
证明:假设 ,
则 。
∴ ,
即 。
这与 矛盾.假设不成立.
∴ .
△ABC中没有一个内角小于或等于60°
∠A>60°,∠B>60°,∠C>60°
∠A+∠B+∠C>180°
三角形的内角和为180度
△ABC中至少有一个内角小于或等于60°.
点拨:至少的反面是没有!
例4
∠A+∠B+∠C>60°+60°+60°=180°
例6、用反证法证明:等腰三角形的底角必定是锐角.
分析:解题的关键是反证法的第一步否定结论,需要分类讨论.
已知:在△ABC中,AB=AC.
求证:∠B、∠C为锐角.
证明:假设等腰三角形的底角不是锐角,那么只有两种情况:
(1)两个底角都是直角;
(2)两个底角都是钝角;
反证法的一般步骤:
假设命题结论不成立
假设不成立
假设命题结论反面成立
与已知条件矛盾
假设
推理得出的结论
与定理,定义,公理矛盾
所证命题成立
什么时候运用反证法呢?
证明真命题 的方法
直接证法
间接证法
反证法
美国总统华盛顿从小非常聪明,小偷翻进鲍克家偷走了许多东西,根据迹象表明小偷就是本村人,华盛顿灵机一动,对全村人讲起了故事:“黄蜂是上帝的使者,能辨别人间的真假.”忽然华盛顿大声喊道:“小偷就是他,黄蜂正在他的帽子上兜圈子,要落下来了!”大家回头张望,看着那个想把帽子上的黄蜂赶走的人,其实哪有什么黄蜂?华盛顿大喝一声:“小偷就是他!”
你知道华盛顿是如何推理的吗?
华盛顿抓小偷
万事开头难,让我们走好第一步!
写出下列各结论的反面:
(1)a//b;
(2)a≥0;
(3)b是正数;
(4)a⊥b
a<0
b是0或负数
a不垂直于b
a∥b
1.在一个梯形中,如果同一条底边上的两个内角不相等,那么这个梯形是等腰梯形吗?请证明你的猜想.
谁来试一试!
2.已知:如图△ABC中,D、E两 点分别在AB和AC上
求证:CD、BE不能互相平分
(平行四边形对边平行)
做一做
学习是件很愉快的事
证明:假设CD、BE互相平分
连结DE,故四边形BCED是平行四边形
∴BD∥CE
这与BD、CE交于点A矛盾
假设错误, ∴CD、BE不能互相平分
四、巩固新知
1、试说出下列命题的反面:
(1)a是实数。 (2)a大于2。
(3)a小于2。 (4)至少有2个
(5)最多有一个 (6)两条直线平行。
2、用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 。
3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步
。
a不是实数
a小于或等于2
a大于或等于2
没有两个
一个也没有
两直线相交
假设a=b
假设这个三角形是等腰三角形
已知:在梯形ABCD中,AB//CD,
∠C≠∠D
求证:梯形ABCD不是等腰梯形.
证明:假设梯形ABCD是等腰梯形。
∴∠C=∠D(等腰梯形同一底上的两内角相等)
这与已知条件∠C≠∠D矛盾, 假设不成立。
∴梯形ABCD不是等腰梯形.
4、求证:如果一个梯形同一底上的两个内角不相等,那么这个梯形不是等腰梯形。
A
B
C
D
五、拓展应用
1、已知:如图,在△ABC中,AB=AC,∠APB≠∠APC。
求证:PB≠PC
A
B
C
P
证明:假设PB=PC。
在△ABP与△ACP中
AB=AC(已知)
AP=AP(公共边)
PB=PC(已知)
∴△ABP≌△ACP(S.S.S)
∴∠APB=∠APC(全等三角形对应边相等)
这与已知条件∠APB≠∠APC矛盾,假设不成立.
∴PB≠PC
美国总统华盛顿从小非常聪明,小偷翻进鲍克家偷走了许多东西,根据迹象表明小偷就是本村人,华盛顿灵机一动,对全村人讲起了故事:“黄蜂是上帝的使者,能辨别人间的真假.”忽然华盛顿大声喊道:“小偷就是他,黄蜂正在他的帽子上兜圈子,要落下来了!”大家回头张望,看着那个想把帽子上的黄蜂赶走的人,其实哪有什么黄蜂?华盛顿大喝一声:“小偷就是他!”
你知道华盛顿是如何推理的吗?
华盛顿抓小偷
警察局里有5名嫌疑犯,他们分别做了如下口供:
A说:这里有1个人说谎.
B说:这里有2个人说谎.
C说:这里有3个人说谎.
D说:这里有4个人说谎.
E说:这里有5个人说谎.
聪明的同学们,假如你是警察,你觉得谁说了真话?
你会释放谁?
请与大家分享你的判断!
六、全课总结
1、知识小结:
反证法证明的思路:假设命题不成立→正确的推理,得出矛盾→肯定待定命题的结论
2、难点提示:
利用反证法证明命题时,一定要准确而全面的找出命题结论的反面。至少的反面是没有,最多的反面是不止。
大家议一议!
通过本节内容的学习,你们觉得哪些题型宜用反证法 ?
我来告诉你(经验之谈)
(1)以否定性判断作为结论的命题;
(2)以“至多”、“至少”或“不多于”等形式陈述的命题;
(3)关于“唯一性”结论的命题;
(4)一些不等量命题的证明;
(5)有些基本定理或某一知识体系的初始阶段等等.(如平行线的传递性的证明)
注意:用反证法证题时,应注意的事项 :
(1)周密考察原命题结论的否定事项,防止否定不当或有所遗漏;
(2)推理过程必须完整,否则不能说明命题的真伪性;
(3)在推理过程中,要充分使用已知条件,否则推不出矛盾,或者不能断定推出的结果是错误的。
课时作业设计
用反证法证明下列命题:
1.求证:三角形内角中至多有一个内角是钝角。
2.已知:如图,AB∥CD,AB ∥EF。
求证:CD ∥EF。
3.求证:圆内两条不是直径的弦不能互相平分。
4.证明“在同一平面内,垂直于同一条直线的两条直线互相平行.”
A
B
C
D
E
F
第2题图
