华师大版八年级上册14.2勾股定理的应用 课件(共15张PPT)
文档属性
| 名称 | 华师大版八年级上册14.2勾股定理的应用 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 09:51:27 | ||
图片预览






文档简介
(共15张PPT)
A
B
C
14.2勾股定理的应用
勾 股 史 话
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理” 。
1.勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
2.怎样判断一个三角形是直角三角形?
如果三角形的三边长分别是a、b、c,满足a2+b2=c2,那么这个三角形是直角三角形.
回顾与思考
勾股定理是几何中非常重要的定理,它揭示直角三角形三条边之间的数量关系,已知任意两边,可以求第三边。它可以解决许多直角三角形中的计算问题,在生产、生活实际中有广范的应用,下面我们学习它的应用。
〈注意〉运用勾股定理必须满足前提条件:在直角三角形中,同时还要明确直角三角形的直角边与斜边。
数形结合思想与勾股定理
勾股定理是反映自然界基本规律的一条重要结论,它有着悠久的历史,在数学发展中起着重要的作用。它揭示了一个直角三角形三条边之间的数量关系,把数与形统一起来,在现实世界中有着广泛的应用.在运用勾股定理解题时,若能正确地把握数形结合的思想方法,则可思路开阔,方法简便快捷。
探究一:一架飞机在天空中水平飞行,某一时刻正好飞到一个男孩头顶正上方3000米处,过了20秒,飞机距离这个男孩头顶5000米,试求这架飞机的飞行速度
20秒
3000米
5000米
A
B
C
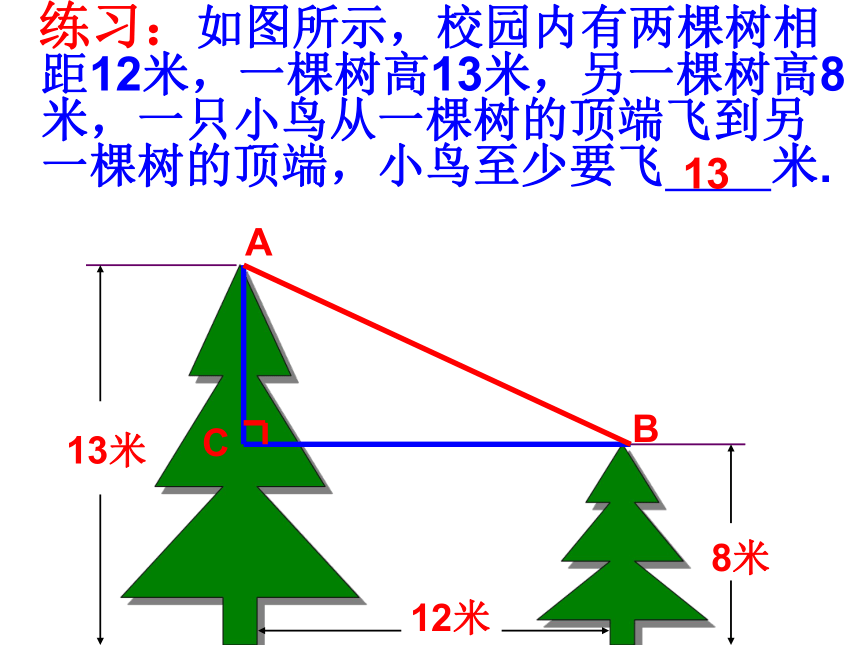
练习:如图所示,校园内有两棵树相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
13米
12米
8米
A
B
C
13
大显身手:
在一棵高4m的树尖上有一只小鸟,它发现离该树12m且高为20m的一棵大树的顶端有一群小鸟,于是它立即飞往去与同伴会合,已知小鸟的飞行速度为4m/s,求小鸟至少需要几秒才能与同伴会合?
一架2.5米长的梯子AB,斜靠在一立直的墙AC上,这时梯子底部B到墙底C的距离为0.7米,如果梯子顶端沿墙垂直下降0.4米.那么梯子底部将外移多少米?
解决问题的关键:在动、静的转化中找出不变的量。
方程思想与勾股定理
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
探究二:名题鉴赏:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
大显身手:
1、 如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
2、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求1、CF ;2.、EC。
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
小结:
通过上述例题讲解的学习,我们发现在应用勾股定理解题时,首先建立数学模型(即建立直角三角形),再将实际问题转化为数学问题,进而解决问题,这充分体现了数形结合与方程的数学思想,同时也体现了数学来源于生活,服务与生活。
课 堂 小 结
1、在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边。
2、在解决实际问题时,首先要画出适当的示将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题.
应用勾股定理解决实际问题的一般思路:
A
B
C
14.2勾股定理的应用
勾 股 史 话
在西方,因为是毕达哥拉斯最先发现这个定理的,所以西方人通常称勾股定理为“毕达哥拉斯定理” .传说毕达哥拉斯证明这个定理之后,杀了一百头牛来庆祝,所以它又叫“百牛定理” .在欧洲中世纪它又被戏称为“驴桥定理” ,因为那时数学水平较低,很多人学习勾股定理时被卡住,难以理解和接受。所以勾股定理被戏称为“驴桥”,意谓笨蛋的难关 。
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就曾提出, “勾三、股四、弦五”,所以勾股定理又叫“商高定理” 。
1.勾股定理的内容是什么?
直角三角形两直角边的平方和等于斜边的平方.
2.怎样判断一个三角形是直角三角形?
如果三角形的三边长分别是a、b、c,满足a2+b2=c2,那么这个三角形是直角三角形.
回顾与思考
勾股定理是几何中非常重要的定理,它揭示直角三角形三条边之间的数量关系,已知任意两边,可以求第三边。它可以解决许多直角三角形中的计算问题,在生产、生活实际中有广范的应用,下面我们学习它的应用。
〈注意〉运用勾股定理必须满足前提条件:在直角三角形中,同时还要明确直角三角形的直角边与斜边。
数形结合思想与勾股定理
勾股定理是反映自然界基本规律的一条重要结论,它有着悠久的历史,在数学发展中起着重要的作用。它揭示了一个直角三角形三条边之间的数量关系,把数与形统一起来,在现实世界中有着广泛的应用.在运用勾股定理解题时,若能正确地把握数形结合的思想方法,则可思路开阔,方法简便快捷。
探究一:一架飞机在天空中水平飞行,某一时刻正好飞到一个男孩头顶正上方3000米处,过了20秒,飞机距离这个男孩头顶5000米,试求这架飞机的飞行速度
20秒
3000米
5000米
A
B
C
练习:如图所示,校园内有两棵树相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
13米
12米
8米
A
B
C
13
大显身手:
在一棵高4m的树尖上有一只小鸟,它发现离该树12m且高为20m的一棵大树的顶端有一群小鸟,于是它立即飞往去与同伴会合,已知小鸟的飞行速度为4m/s,求小鸟至少需要几秒才能与同伴会合?
一架2.5米长的梯子AB,斜靠在一立直的墙AC上,这时梯子底部B到墙底C的距离为0.7米,如果梯子顶端沿墙垂直下降0.4米.那么梯子底部将外移多少米?
解决问题的关键:在动、静的转化中找出不变的量。
方程思想与勾股定理
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
探究二:名题鉴赏:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
大显身手:
1、 如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
2、折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求1、CF ;2.、EC。
A
B
C
D
E
F
8
10
10
6
X
8-X
4
8-X
小结:
通过上述例题讲解的学习,我们发现在应用勾股定理解题时,首先建立数学模型(即建立直角三角形),再将实际问题转化为数学问题,进而解决问题,这充分体现了数形结合与方程的数学思想,同时也体现了数学来源于生活,服务与生活。
课 堂 小 结
1、在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边。
2、在解决实际问题时,首先要画出适当的示将实际问题抽象为数学问题,并构建直角三角形模型,再运用勾股定理解决实际问题.
应用勾股定理解决实际问题的一般思路:
