2022年高考数学真题分类汇编——三角函数等部分(含解析)
文档属性
| 名称 | 2022年高考数学真题分类汇编——三角函数等部分(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 20:06:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2022年高考数学真题分类汇编——三角函数等部分
一.选择题(共10小题)
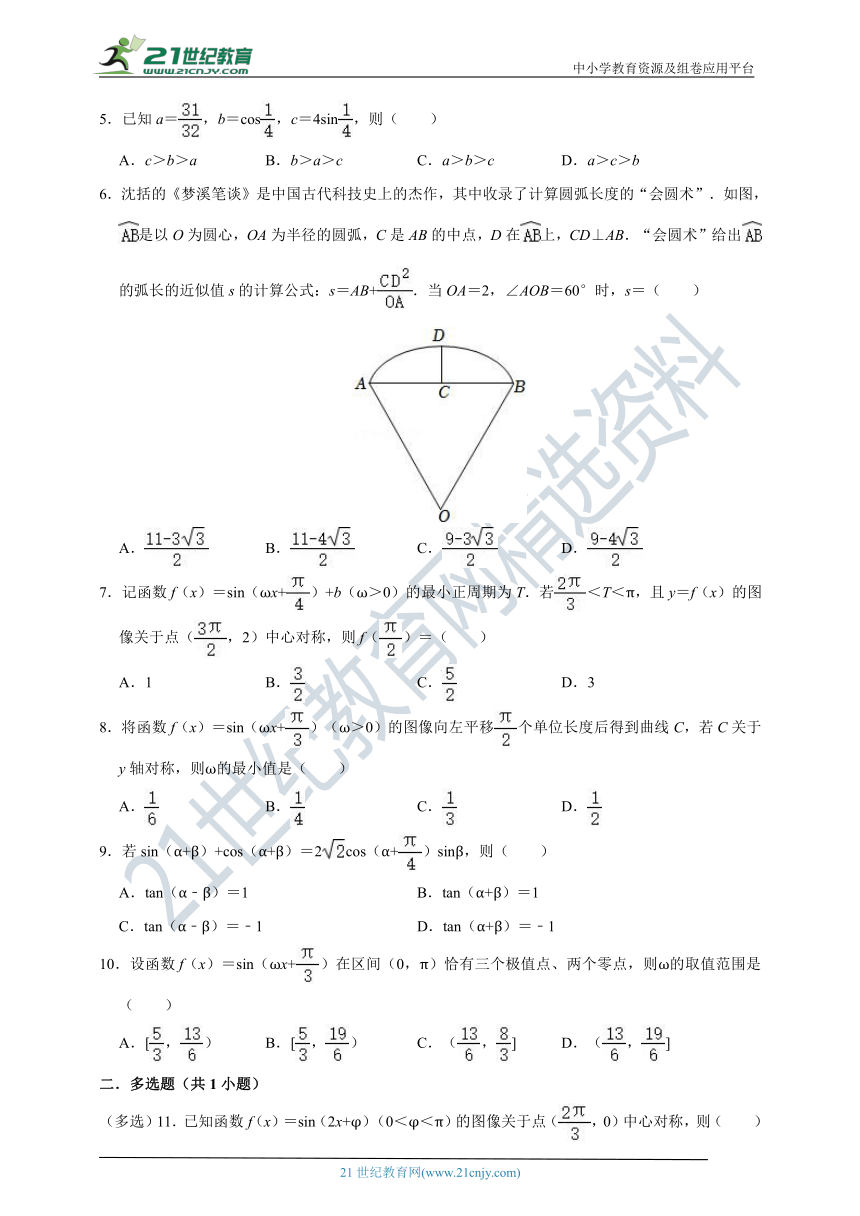
1.执行如图的程序框图,输出的n=( )
A.3 B.4 C.5 D.6
2.嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{bn}:b1=1+,b2=1+,b3=1+,…,依此类推,其中αk∈N*(k=1,2,…).则( )
A.b1<b5 B.b3<b8 C.b6<b2 D.b4<b7
3.为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
4.已知函数f(x)=cos2x﹣sin2x,则( )
A.f(x)在(﹣,﹣)上单调递减 B.f(x)在(﹣,)上单调递增
C.f(x)在(0,)上单调递减 D.f(x)在(,)上单调递增
5.已知a=,b=cos,c=4sin,则( )
A.c>b>a B.b>a>c C.a>b>c D.a>c>b
6.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,OA为半径的圆弧,C是AB的中点,D在上,CD⊥AB.“会圆术”给出的弧长的近似值s的计算公式:s=AB+.当OA=2,∠AOB=60°时,s=( )
A. B. C. D.
7.记函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T.若<T<π,且y=f(x)的图像关于点(,2)中心对称,则f()=( )
A.1 B. C. D.3
8.将函数f(x)=sin(ωx+)(ω>0)的图像向左平移个单位长度后得到曲线C,若C关于y轴对称,则ω的最小值是( )
A. B. C. D.
9.若sin(α+β)+cos(α+β)=2cos(α+)sinβ,则( )
A.tan(α﹣β)=1 B.tan(α+β)=1
C.tan(α﹣β)=﹣1 D.tan(α+β)=﹣1
10.设函数f(x)=sin(ωx+)在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是( )
A.[,) B.[,) C.(,] D.(,]
二.多选题(共1小题)
(多选)11.已知函数f(x)=sin(2x+φ)(0<φ<π)的图像关于点(,0)中心对称,则( )
A.f(x)在区间(0,)单调递减 B.f(x)在区间(﹣,)有两个极值点
C.直线x=是曲线y=f(x)的对称轴 D.直线y=﹣x是曲线y=f(x)的切线
三.填空题(共6小题)
12.若3sinα﹣sinβ=,α+β=,则sinα= ,cos2β= .
13.若函数f(x)=Asinx﹣cosx的一个零点为,则A= ;f()= .
14.已知△ABC中,点D在边BC上,∠ADB=120°,AD=2,CD=2BD.当取得最小值时,BD= .
15.记函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期为T.若f(T)=,x=为f(x)的零点,则ω的最小值为 .
16.若tanα=3,则tan(α+)= .
17.已知在△ABC中,∠A=,AB=2,AC=3,则△ABC的外接圆半径为 .
四.解答题(共6小题)
18.在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
19.在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
20.记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A﹣B)=sinBsin(C﹣A).
(1)若A=2B,求C;
(2)证明:2a2=b2+c2.
21.记△ABC的内角A,B,C的对边分别为a,b,c,分别以a,b,c为边长的三个正三角形的面积依次为S1,S2,S3.已知S1﹣S2+S3=,sinB=.
(1)求△ABC的面积;
(2)若sinAsinC=,求b.
22.记△ABC的内角A,B,C的对边分别为a,b,c,已知=.
(1)若C=,求B;
(2)求的最小值.
23.记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A﹣B)=sinBsin(C﹣A).
(1)证明:2a2=b2+c2;
(2)若a=5,cosA=,求△ABC的周长.
2022年高考数学真题分类汇编——三角函数等部分
参考答案与试题解析
一.选择题(共10小题)
1.【解答】模拟执行程序的运行过程,如下:
输入a=1,b=1,n=1,
计算b=1+2=3,a=3﹣1=2,n=2,
判断|﹣2|==0.25≥0.01,
计算b=3+4=7,a=7﹣2=5,n=3,
判断|﹣2|==0.04≥0.01;
计算b=7+10=17,a=17﹣5=12,n=4,
判断|﹣2|=<0.01;
输出n=4.
故选:B.
2.【解答】∵αk∈N*(k=1,2,…),∴可以取αk=1,
则b1=1+=2,
b2=1+=,
b3=1+=,
b4=1+=,
b5=1+=,
b6=1+=,
b7==,
b8=1+=,
∴b1>b5,故A错误;b3>b8,故B错误;b6>b2,故C错误;b4<b7,故D正确.
故选:D.
3.【解答】把y=2sin(3x+)图象上所有的点向右平移各单位可得y=2sin[3(x﹣)+]=2sin3x的图象.
故选:D.
4.【解答】f(x)=cos2x﹣sin2x=cos2x,周期T=π,
∴f(x)的单调递减区间为[kπ,](k∈Z),单调递增区间为[,π+kπ](k∈Z),
对于A,f(x)在(﹣,﹣)上单调递增,故A错误,
对于B,f(x)在(﹣,0)上单调递增,在(0,)上单调递减,故B错误,
对于C,f(x)在(0,)上单调递减,故C正确,
对于D,f(x)在(,)上单调递减,在(,)上单调递增,故D错误,
故选:C.
5.【解答】设f(x)=cosx+,(0<x<1),则f′(x)=x﹣sinx,
设g(x)=x﹣sinx(0<x<1),g′(x)=1﹣cosx>0,
故g(x)在(0,1)单调递增,即g(x)>g(0)=0,
即f′(x)>0,故f(x)(0,1)单调递增,
所以f()>f(0)=0,可得cos,故b>a,
利用三角函数线可得x)时,tanx>x,
∴tan>,即,∴4sin,故c>b.
综上:c>b>a,
故选:A.
6.【解答】∵OA=OB=2,∠AOB=60°,∴AB=2,
∵C是AB的中点,D在上,CD⊥AB,
∴延长DC可得O在DC上,CD=OD﹣OC=2﹣,
∴s=AB+=2+=2+=.
故选:B.
7.【解答】函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T,
则T=,由<T<π,得<<π,∴2<ω<3,
∵y=f(x)的图像关于点(,2)中心对称,∴b=2,
且sin(+)=0,则+=kπ,k∈Z.
∴,k∈Z,取k=4,可得.
∴f(x)=sin(x+)+2,则f()=sin(×+)+2=﹣1+2=1.
故选:A.
8.【解答】将函数f(x)=sin(ωx+)(ω>0)的图像向左平移个单位长度后得到曲线C,
则C对应函数为y=sin(ωx++),
∵C的图象关于y轴对称,∴+=kπ+,k∈Z,
即ω=2k+,k∈Z,
则令k=0,可得ω的最小值是,
故选:C.
9.【解答】因为sin(α+β)+cos(α+β)=2cos(α+)sinβ,
所以sin()=2cos(α+)sinβ,
即sin()=2cos(α+)sinβ,
所以sin()cosβ+sinβcos()=2cos(α+)sinβ,
所以sin()cosβ﹣sinβcos()=0,
所以sin()=0,
所以=kπ,k∈Z,
所以α﹣β=k,
所以tan(α﹣β)=﹣1.
故选:C.
10.【解答】当ω<0时,不能满足在区间(0,π)极值点比零点多,所以ω>0;
函数f(x)=sin(ωx+)在区间(0,π)恰有三个极值点、两个零点,
ωx+∈(,ωπ+),
∴<ωπ+≤3π,
求得<ω≤,
故选:C.
二.多选题(共1小题)
11.【解答】因为f(x)=sin(2x+φ)(0<φ<π)的图象关于点(,0)对称,
所以+φ=kπ,k∈Z,
所以φ=kπ﹣,
因为0<φ<π,
所以φ=,
故f(x)=sin(2x+),
令2x+,解得﹣<x<,
故f(x)在(0,)单调递减,A正确;
x∈(﹣,),2x+∈(,),
根据函数的单调性,故函数f(x)在区间(﹣,)只有一个极值点,故B错误;
令2x+=kπ+,k∈Z,得x=﹣,k∈Z,C显然错误;
结合正弦函数的图象可知,
直线y=显然与y=sin(2x+)相切,故直线y=显然是曲线的切线,故D正确.
故选:AD.
三.填空题(共6小题)
12.【解答】∵3sinα﹣sinβ=,α+β=,
∴3sinα﹣cosα=,
∴cosα=3sinα﹣,
∵sin2α+cos2α=1,
∴sin2α+(3sin)2=1,
解得sinα=,cosβ=sinα=,
cos2β=2cos2β﹣1=2×﹣1=.
故答案为:;.
13.【解答】∵函数f(x)=Asinx﹣cosx的一个零点为,∴A﹣×=0,
∴A=1,函数f(x)=sinx﹣cosx=2sin(x﹣),
∴f()=2sin(﹣)=2sin(﹣)=﹣2sin=﹣,
故答案为:1;﹣.
14.【解答】设BD=x,CD=2x,
在三角形ACD中,b2=4x2+4﹣2 2x 2 cos60°,可得:b2=4x2﹣4x+4,
在三角形ABD中,c2=x2+4﹣2 x 2 cos120°,可得:c2=x2+2x+4,
要使得最小,即最小,
==,
其中,此时,
当且仅当时,即时取等号,
故答案为:.
15.【解答】函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期为T=,
若f(T)=cos(ω×+φ)=cosφ=,0<φ<π,则φ=,
所以f(x)=cos(ωx+).
因为x=为f(x)的零点,所以cos(+)=0,
故 +=k,k∈Z,所以ω=9k+3,k∈Z,
因为ω>0,则ω的最小值为3.
故答案为:3.
16.【解答】若tanα=3,
则tan(α+)===﹣2.
故答案为:﹣2.
17.【解答】在△ABC中,∠A=,AB=2,AC=3,
利用余弦定理BC2=AC2+AB2﹣2AB AC cosA,整理得BC=,
所以,解得R=.
故答案为:.
四.解答题(共6小题)
18.【解答】(Ⅰ)因为cosC=>0,所以C∈(0,),且sinC==,
由正弦定理可得:=,
即有sinA==sinC=×=;
(Ⅱ)因为4a=c a=c<c,
所以A<C,故A∈(0,),
又因为sinA=,所以cosA=,
所以sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC=;
由正弦定理可得:===5,
所以a=5sinA=5,
所以S△ABC=absinC=×5×11×=22.
19.【解答】(Ⅰ)∵sin2C=sinC,
∴2sinCcosC=sinC,
又sinC≠0,∴2cosC=,
∴cosC=,∵0<C<π,
∴C=;
(Ⅱ)∵△ABC的面积为6,
∴absinC=6,
又b=6,C=,
∴×a×6×=6,
∴a=4,
又cosC=,
∴=,
∴c=2,
∴a+b+c=6+6,
∴△ABC的周长为6+6.
20.【解答】(1)由sinCsin(A﹣B)=sinBsin(C﹣A),
又A=2B,∴sinCsinB=sinBsin(C﹣A),
∵sinB≠0,∴sinC=sin(C﹣A),即C=C﹣A(舍去)或C+C﹣A=π,
联立,解得C=;
证明:(2)由sinCsin(A﹣B)=sinBsin(C﹣A),
得sinCsinAcosB﹣sinCcosAsinB=sinBsinCcosA﹣sinBcosCsinA,
由正弦定理可得accosB﹣bccosA=bccosA﹣abcosC,
由余弦定理可得:ac ,
整理可得:2a2=b2+c2.
21.【解答】(1)S1=a2sin60°=a2,
S2=b2sin60°=b2,
S3=c2sin60°=c2,
∵S1﹣S2+S3=a2﹣b2+c2=,
解得:a2﹣b2+c2=2,
∵sinB=,a2﹣b2+c2=2>0,即cosB>0,
∴cosB=,
∴cosB==,
解得:ac=,
S△ABC=acsinB=.
∴△ABC的面积为.
(2)由正弦定理得:==,
∴a=,c=,
由(1)得ac=,
∴ac= =
已知,sinB=,sinAsinC=,
解得:b=.
22.【解答】(1)∵=,1+cos2B=2cos2B≠0,cosB≠0.
∴==,
化为:cosAcosB=sinAsinB+sinB,
∴cos(B+A)=sinB,
∴﹣cosC=sinB,C=,
∴sinB=,
∵0<B<,∴B=.
(2)由(1)可得:﹣cosC=sinB>0,∴cosC<0,C∈(,π),
∴C为钝角,B,A都为锐角,B=C﹣.
sinA=sin(B+C)=sin(2C﹣)=﹣cos2C,
=====+4sin2C﹣5≥2﹣5=4﹣5,当且仅当sinC=时取等号.
∴的最小值为4﹣5.
23.【解答】(1)证明:△ABC中,sinCsin(A﹣B)=sinBsin(C﹣A),
所以sinC(sinAcosB﹣cosAsinB)=sinB(sinCcosA﹣cosCsinA),
所以sinAsinBcosC+sinAcosBsinC=2cosAsinBsinC,
即sinA(sinBcosC+cosBsinC)=2cosAsinBsinC,
所以sinAsin(B+C)=2cosAsinBsinC,
由正弦定理得a2=2bccosA,
由余弦定理得a2=b2+c2﹣2bccosA,
所以2a2=b2+c2;
(2)当a=5,cosA=时,b2+c2=2×52=50,2bc===31,
所以(b+c)2=b2+c2+2bc=50+31=81,解得b+c=9,
所以△ABC的周长为a+b+c=5+9=14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2022年高考数学真题分类汇编——三角函数等部分
一.选择题(共10小题)
1.执行如图的程序框图,输出的n=( )
A.3 B.4 C.5 D.6
2.嫦娥二号卫星在完成探月任务后,继续进行深空探测,成为我国第一颗环绕太阳飞行的人造行星.为研究嫦娥二号绕日周期与地球绕日周期的比值,用到数列{bn}:b1=1+,b2=1+,b3=1+,…,依此类推,其中αk∈N*(k=1,2,…).则( )
A.b1<b5 B.b3<b8 C.b6<b2 D.b4<b7
3.为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度 B.向右平移个单位长度
C.向左平移个单位长度 D.向右平移个单位长度
4.已知函数f(x)=cos2x﹣sin2x,则( )
A.f(x)在(﹣,﹣)上单调递减 B.f(x)在(﹣,)上单调递增
C.f(x)在(0,)上单调递减 D.f(x)在(,)上单调递增
5.已知a=,b=cos,c=4sin,则( )
A.c>b>a B.b>a>c C.a>b>c D.a>c>b
6.沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,是以O为圆心,OA为半径的圆弧,C是AB的中点,D在上,CD⊥AB.“会圆术”给出的弧长的近似值s的计算公式:s=AB+.当OA=2,∠AOB=60°时,s=( )
A. B. C. D.
7.记函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T.若<T<π,且y=f(x)的图像关于点(,2)中心对称,则f()=( )
A.1 B. C. D.3
8.将函数f(x)=sin(ωx+)(ω>0)的图像向左平移个单位长度后得到曲线C,若C关于y轴对称,则ω的最小值是( )
A. B. C. D.
9.若sin(α+β)+cos(α+β)=2cos(α+)sinβ,则( )
A.tan(α﹣β)=1 B.tan(α+β)=1
C.tan(α﹣β)=﹣1 D.tan(α+β)=﹣1
10.设函数f(x)=sin(ωx+)在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是( )
A.[,) B.[,) C.(,] D.(,]
二.多选题(共1小题)
(多选)11.已知函数f(x)=sin(2x+φ)(0<φ<π)的图像关于点(,0)中心对称,则( )
A.f(x)在区间(0,)单调递减 B.f(x)在区间(﹣,)有两个极值点
C.直线x=是曲线y=f(x)的对称轴 D.直线y=﹣x是曲线y=f(x)的切线
三.填空题(共6小题)
12.若3sinα﹣sinβ=,α+β=,则sinα= ,cos2β= .
13.若函数f(x)=Asinx﹣cosx的一个零点为,则A= ;f()= .
14.已知△ABC中,点D在边BC上,∠ADB=120°,AD=2,CD=2BD.当取得最小值时,BD= .
15.记函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期为T.若f(T)=,x=为f(x)的零点,则ω的最小值为 .
16.若tanα=3,则tan(α+)= .
17.已知在△ABC中,∠A=,AB=2,AC=3,则△ABC的外接圆半径为 .
四.解答题(共6小题)
18.在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
19.在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
20.记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A﹣B)=sinBsin(C﹣A).
(1)若A=2B,求C;
(2)证明:2a2=b2+c2.
21.记△ABC的内角A,B,C的对边分别为a,b,c,分别以a,b,c为边长的三个正三角形的面积依次为S1,S2,S3.已知S1﹣S2+S3=,sinB=.
(1)求△ABC的面积;
(2)若sinAsinC=,求b.
22.记△ABC的内角A,B,C的对边分别为a,b,c,已知=.
(1)若C=,求B;
(2)求的最小值.
23.记△ABC的内角A,B,C的对边分别为a,b,c,已知sinCsin(A﹣B)=sinBsin(C﹣A).
(1)证明:2a2=b2+c2;
(2)若a=5,cosA=,求△ABC的周长.
2022年高考数学真题分类汇编——三角函数等部分
参考答案与试题解析
一.选择题(共10小题)
1.【解答】模拟执行程序的运行过程,如下:
输入a=1,b=1,n=1,
计算b=1+2=3,a=3﹣1=2,n=2,
判断|﹣2|==0.25≥0.01,
计算b=3+4=7,a=7﹣2=5,n=3,
判断|﹣2|==0.04≥0.01;
计算b=7+10=17,a=17﹣5=12,n=4,
判断|﹣2|=<0.01;
输出n=4.
故选:B.
2.【解答】∵αk∈N*(k=1,2,…),∴可以取αk=1,
则b1=1+=2,
b2=1+=,
b3=1+=,
b4=1+=,
b5=1+=,
b6=1+=,
b7==,
b8=1+=,
∴b1>b5,故A错误;b3>b8,故B错误;b6>b2,故C错误;b4<b7,故D正确.
故选:D.
3.【解答】把y=2sin(3x+)图象上所有的点向右平移各单位可得y=2sin[3(x﹣)+]=2sin3x的图象.
故选:D.
4.【解答】f(x)=cos2x﹣sin2x=cos2x,周期T=π,
∴f(x)的单调递减区间为[kπ,](k∈Z),单调递增区间为[,π+kπ](k∈Z),
对于A,f(x)在(﹣,﹣)上单调递增,故A错误,
对于B,f(x)在(﹣,0)上单调递增,在(0,)上单调递减,故B错误,
对于C,f(x)在(0,)上单调递减,故C正确,
对于D,f(x)在(,)上单调递减,在(,)上单调递增,故D错误,
故选:C.
5.【解答】设f(x)=cosx+,(0<x<1),则f′(x)=x﹣sinx,
设g(x)=x﹣sinx(0<x<1),g′(x)=1﹣cosx>0,
故g(x)在(0,1)单调递增,即g(x)>g(0)=0,
即f′(x)>0,故f(x)(0,1)单调递增,
所以f()>f(0)=0,可得cos,故b>a,
利用三角函数线可得x)时,tanx>x,
∴tan>,即,∴4sin,故c>b.
综上:c>b>a,
故选:A.
6.【解答】∵OA=OB=2,∠AOB=60°,∴AB=2,
∵C是AB的中点,D在上,CD⊥AB,
∴延长DC可得O在DC上,CD=OD﹣OC=2﹣,
∴s=AB+=2+=2+=.
故选:B.
7.【解答】函数f(x)=sin(ωx+)+b(ω>0)的最小正周期为T,
则T=,由<T<π,得<<π,∴2<ω<3,
∵y=f(x)的图像关于点(,2)中心对称,∴b=2,
且sin(+)=0,则+=kπ,k∈Z.
∴,k∈Z,取k=4,可得.
∴f(x)=sin(x+)+2,则f()=sin(×+)+2=﹣1+2=1.
故选:A.
8.【解答】将函数f(x)=sin(ωx+)(ω>0)的图像向左平移个单位长度后得到曲线C,
则C对应函数为y=sin(ωx++),
∵C的图象关于y轴对称,∴+=kπ+,k∈Z,
即ω=2k+,k∈Z,
则令k=0,可得ω的最小值是,
故选:C.
9.【解答】因为sin(α+β)+cos(α+β)=2cos(α+)sinβ,
所以sin()=2cos(α+)sinβ,
即sin()=2cos(α+)sinβ,
所以sin()cosβ+sinβcos()=2cos(α+)sinβ,
所以sin()cosβ﹣sinβcos()=0,
所以sin()=0,
所以=kπ,k∈Z,
所以α﹣β=k,
所以tan(α﹣β)=﹣1.
故选:C.
10.【解答】当ω<0时,不能满足在区间(0,π)极值点比零点多,所以ω>0;
函数f(x)=sin(ωx+)在区间(0,π)恰有三个极值点、两个零点,
ωx+∈(,ωπ+),
∴<ωπ+≤3π,
求得<ω≤,
故选:C.
二.多选题(共1小题)
11.【解答】因为f(x)=sin(2x+φ)(0<φ<π)的图象关于点(,0)对称,
所以+φ=kπ,k∈Z,
所以φ=kπ﹣,
因为0<φ<π,
所以φ=,
故f(x)=sin(2x+),
令2x+,解得﹣<x<,
故f(x)在(0,)单调递减,A正确;
x∈(﹣,),2x+∈(,),
根据函数的单调性,故函数f(x)在区间(﹣,)只有一个极值点,故B错误;
令2x+=kπ+,k∈Z,得x=﹣,k∈Z,C显然错误;
结合正弦函数的图象可知,
直线y=显然与y=sin(2x+)相切,故直线y=显然是曲线的切线,故D正确.
故选:AD.
三.填空题(共6小题)
12.【解答】∵3sinα﹣sinβ=,α+β=,
∴3sinα﹣cosα=,
∴cosα=3sinα﹣,
∵sin2α+cos2α=1,
∴sin2α+(3sin)2=1,
解得sinα=,cosβ=sinα=,
cos2β=2cos2β﹣1=2×﹣1=.
故答案为:;.
13.【解答】∵函数f(x)=Asinx﹣cosx的一个零点为,∴A﹣×=0,
∴A=1,函数f(x)=sinx﹣cosx=2sin(x﹣),
∴f()=2sin(﹣)=2sin(﹣)=﹣2sin=﹣,
故答案为:1;﹣.
14.【解答】设BD=x,CD=2x,
在三角形ACD中,b2=4x2+4﹣2 2x 2 cos60°,可得:b2=4x2﹣4x+4,
在三角形ABD中,c2=x2+4﹣2 x 2 cos120°,可得:c2=x2+2x+4,
要使得最小,即最小,
==,
其中,此时,
当且仅当时,即时取等号,
故答案为:.
15.【解答】函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)的最小正周期为T=,
若f(T)=cos(ω×+φ)=cosφ=,0<φ<π,则φ=,
所以f(x)=cos(ωx+).
因为x=为f(x)的零点,所以cos(+)=0,
故 +=k,k∈Z,所以ω=9k+3,k∈Z,
因为ω>0,则ω的最小值为3.
故答案为:3.
16.【解答】若tanα=3,
则tan(α+)===﹣2.
故答案为:﹣2.
17.【解答】在△ABC中,∠A=,AB=2,AC=3,
利用余弦定理BC2=AC2+AB2﹣2AB AC cosA,整理得BC=,
所以,解得R=.
故答案为:.
四.解答题(共6小题)
18.【解答】(Ⅰ)因为cosC=>0,所以C∈(0,),且sinC==,
由正弦定理可得:=,
即有sinA==sinC=×=;
(Ⅱ)因为4a=c a=c<c,
所以A<C,故A∈(0,),
又因为sinA=,所以cosA=,
所以sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC=;
由正弦定理可得:===5,
所以a=5sinA=5,
所以S△ABC=absinC=×5×11×=22.
19.【解答】(Ⅰ)∵sin2C=sinC,
∴2sinCcosC=sinC,
又sinC≠0,∴2cosC=,
∴cosC=,∵0<C<π,
∴C=;
(Ⅱ)∵△ABC的面积为6,
∴absinC=6,
又b=6,C=,
∴×a×6×=6,
∴a=4,
又cosC=,
∴=,
∴c=2,
∴a+b+c=6+6,
∴△ABC的周长为6+6.
20.【解答】(1)由sinCsin(A﹣B)=sinBsin(C﹣A),
又A=2B,∴sinCsinB=sinBsin(C﹣A),
∵sinB≠0,∴sinC=sin(C﹣A),即C=C﹣A(舍去)或C+C﹣A=π,
联立,解得C=;
证明:(2)由sinCsin(A﹣B)=sinBsin(C﹣A),
得sinCsinAcosB﹣sinCcosAsinB=sinBsinCcosA﹣sinBcosCsinA,
由正弦定理可得accosB﹣bccosA=bccosA﹣abcosC,
由余弦定理可得:ac ,
整理可得:2a2=b2+c2.
21.【解答】(1)S1=a2sin60°=a2,
S2=b2sin60°=b2,
S3=c2sin60°=c2,
∵S1﹣S2+S3=a2﹣b2+c2=,
解得:a2﹣b2+c2=2,
∵sinB=,a2﹣b2+c2=2>0,即cosB>0,
∴cosB=,
∴cosB==,
解得:ac=,
S△ABC=acsinB=.
∴△ABC的面积为.
(2)由正弦定理得:==,
∴a=,c=,
由(1)得ac=,
∴ac= =
已知,sinB=,sinAsinC=,
解得:b=.
22.【解答】(1)∵=,1+cos2B=2cos2B≠0,cosB≠0.
∴==,
化为:cosAcosB=sinAsinB+sinB,
∴cos(B+A)=sinB,
∴﹣cosC=sinB,C=,
∴sinB=,
∵0<B<,∴B=.
(2)由(1)可得:﹣cosC=sinB>0,∴cosC<0,C∈(,π),
∴C为钝角,B,A都为锐角,B=C﹣.
sinA=sin(B+C)=sin(2C﹣)=﹣cos2C,
=====+4sin2C﹣5≥2﹣5=4﹣5,当且仅当sinC=时取等号.
∴的最小值为4﹣5.
23.【解答】(1)证明:△ABC中,sinCsin(A﹣B)=sinBsin(C﹣A),
所以sinC(sinAcosB﹣cosAsinB)=sinB(sinCcosA﹣cosCsinA),
所以sinAsinBcosC+sinAcosBsinC=2cosAsinBsinC,
即sinA(sinBcosC+cosBsinC)=2cosAsinBsinC,
所以sinAsin(B+C)=2cosAsinBsinC,
由正弦定理得a2=2bccosA,
由余弦定理得a2=b2+c2﹣2bccosA,
所以2a2=b2+c2;
(2)当a=5,cosA=时,b2+c2=2×52=50,2bc===31,
所以(b+c)2=b2+c2+2bc=50+31=81,解得b+c=9,
所以△ABC的周长为a+b+c=5+9=14.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
