2021-2022学年高二上学期人教A版数学选修2-1:1.3简单的逻辑联结词 课件(共29张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期人教A版数学选修2-1:1.3简单的逻辑联结词 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 817.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 11:54:31 | ||
图片预览







文档简介
(共29张PPT)
1.3 简单的逻辑连接词
且(and)
第一章 常用逻辑用语
或(or)
非(not)
p
q
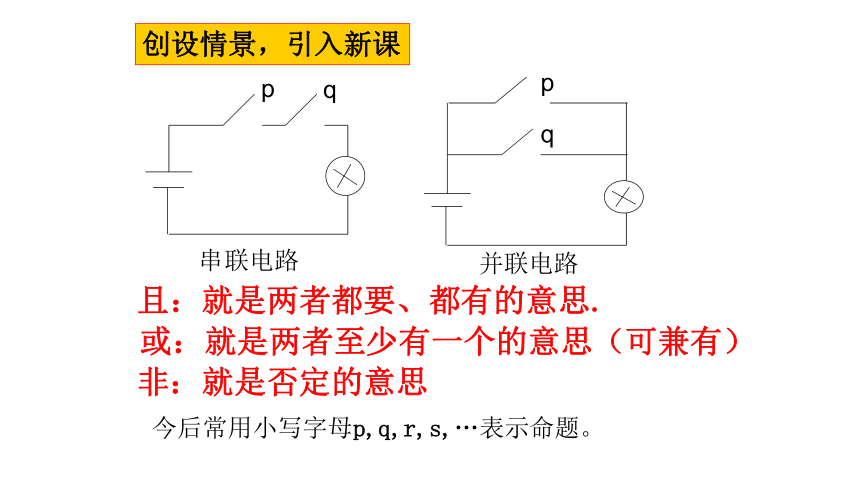
串联电路
创设情景,引入新课
且:就是两者都要、都有的意思.
p
q
并联电路
或:就是两者至少有一个的意思(可兼有)
非:就是否定的意思
今后常用小写字母p,q,r,s,…表示命题。
探究新知,巩固练习
★★ 1.3.1 且 (and)
下列命题中,命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除;
1.问题1:
思考:
命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题.
一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q”
填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .
一句话概括:
全真为真,有假即假.
真命题
假命题
命题p∧q的真假判断方法:
p q p ∧ q
真 真
真 假
假 真
假 假
假
假
假
真
探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢?
对“且”的理解,可联想到集合中“交集”的概念.A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思
活动探究
有些命题如含有“……和……”、“……与……”、“既……,又…..”等词的命题能用“且”改写成“p∧q”的形式,
★★1.3.2 或 (or)
下列命题中,命题 间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.
1.问题1:
思考:
命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.
一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
一句话概括:
有真即真, 全假为假.
一
真
假
命题p∨q的真假判断方法:
p q p∨q
真 真
真 假
假 真
假 假
假
真
真
真
探究:逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢?
对“或”的理解,可联想到集合中“并集”的概念.A∪B={x︱x∈A或x∈B}中的“或”,它是指
“x∈A”、“x∈B”中至少一个是成立的,即x∈A且
x B;也可以x A且x∈B;也可以x∈A且x∈B.
活动探究
如果p∧q为真命题,那么p∨q一定是真命题吗 反之,如果p∨q为真命题,那么p∧q一定是真命题吗
总结思考
p∧q为真命题 p∨q是真命题
p∨q是真命题 p∧q为真命题
下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根
★★1.3.3 非 (not)
一般地,对一个命题p全盘否定,就得到一个新命题,记作 p,读作“非p”或“p的否定”.
命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.
思考:
1.问题1
填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?
一句话概括:
真假相反
p与┐p真假性相反
真命题
假命题
p p
真
假
假
真
对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.
探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?
活动探究
探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?
命题的否定与否命题是完全不同的概念
(1)原命题“若P则q” 的形式,它的非命题“若p,则 q”;而它的否命题为 “若┓p,则┓q”.
(2)命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.
命题的否定与否命题的区别
例:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:
正方形的四条边不相等.
若一个四边形不是正方形,则它的四条边不相等.
原词语 否定词 原词语 否定词
等于 任意的
是 至少有一个
都是 至多有一个
大于 至少有n个
小于 至多有n个
一些常见的结论的否定形式
不是
不都是
不大于
大于或等于
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
不等于
某个
“或”的否定是“且”
p q 非p p且q p或q
真 真 假 真 真
真 假 假 假 真
假 真 真 假 真
假 假 真 假 假
真值表:
非p 真假相反
p且q 一假必假
p或q 一真必真
“或”:不等式 x2 x 6>0的解集{ x | x< 2或x>3 }
“且”:不等式 x2 x 6<0的解集 { x | 2< x<3 }
即 { x | x> 2且x<3 }
“非”:三角形的内角和不大于180°
“或” A∪B={x|x∈A或x∈B}
“且” A∩B={x|x∈A且x∈B}
“非” UA={x|x∈U且x A}
“或”、“且”、“非”与集合的意义相同吗
拓展延伸
例1、设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p∨q为真,p∧q为假,求m的取值范围.
解:若方程x2+mx+1=0有两个不等的负根
即 p: m>2
若方程4x2+4(m-2)x+1=0无实根
则 =16(m-2)2-16<0,
即1∴ m>2
∴q:1< m<3
∵p或q为真,则p,q至少一个为真,又p且q为假,则p,q至少一个为假
∴p,q一真一假,p真q假或者p假q真
例2、已知命题 二次函数 在 上是增函数;命题 指数函数
在定义域内是增函数;
命题“ ”为假,且“ ”为假,
求实数 的取值范围.
解:若 为真,则
若 为真,则
由题意可知 真 假,
∵ 是 的必要不充分条件,
∴ 是 的必要不充分条件,
∴ 是 的充分不必要条件.
解:命题 等价于:
例4、设命题p:函数f(x)=lg(ax2-x+ )的定义域为R;命题q:关于x的不等式3x-9x(1)如果p是真命题,求实数a的取值范围;
若命题p为真命题,
当a=0时,-x>0,不合题意;
解答
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
由x>0,得3x>1,∴y=3x-9x的值域为(-∞,0).
若命题q为真命题,则a≥0.
由命题“p或q”为真命题,且“p且q”为假命题,得命题p,q一真一假.
当p真q假时,a不存在;当p假q真时,0≤a≤2.
∴满足条件的a的取值范围是{a|0≤a≤2}.
解答
例5、已知命题p:函数f(x)=(x+m)(x+4)为偶函数;命题q:方程x2+(2m-1)x+4-2m=0的一个根大于2,一个根小于2,若p∧q为假,p∨q为真,求实数m的取值范围.
若命题p为真,则由f(x)=x2+(m+4)x+4m,得m+4=0,解得m=-4.
设g(x)=x2+(2m-1)x+4-2m,其图象开口向上,
若命题q为真,则g(2)<0,即22+(2m-1)×2+4-2m<0,解得m<-3.
由p∧q为假,p∨q为真,得p假q真或p真q假.
若p假q真,则m<-3且m≠-4;
若p真q假,则m无解.
所以m的取值范围为(-∞,-4)∪(-4,-3).
解答
例6、.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用p、q及逻辑联结词“或”、“且”、“非”表示下列命题:
(1)两次射击至少有一次中靶;
(2)两次射击一次都没有中靶.
p∨q
(┐p) ()
例7、已知命题p:若,则恒成立;q:的充要条件是则下列命题为真命题的是( )
D
例8、若命题p:,则┐p是( )
A. B.
C. D.
例10、已知命题p:点M(1,2)在不等式表示的区域内;
q:直线与直线相交.若为真命题,则实数m的取值范围.
例9、已知命题[p (┐q)] [(┐p) (┐q)]为真命题,则( )
A. 都为真 B. 都为假 C. D. 真
一个或多个逻辑联结词设计新的真命题!
其中真命题的是( )
C
甲,乙,丙三位同学中的一位在昨天晚上放学后把教室打扫干净了,今天早上,老师问她们三个人是谁做的好事。
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
已知只有一位同学说的是真话,你们能帮助老师找出是谁做的吗?
趣味情景
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
甲说
的是真话
乙说
的是假话
丙说
的是假话
是我做的
是我做的
是乙做的
矛盾!
丙说
的是真话
甲说
的是假话
乙说
的是假话
不是乙做的
是我做的
不是我做的
矛盾!
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
乙说
的是真话
甲说
的是假话
丙说
的是假话
不是乙做的
是我做的
不是我做的
不矛盾!
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
1.3 简单的逻辑连接词
且(and)
第一章 常用逻辑用语
或(or)
非(not)
p
q
串联电路
创设情景,引入新课
且:就是两者都要、都有的意思.
p
q
并联电路
或:就是两者至少有一个的意思(可兼有)
非:就是否定的意思
今后常用小写字母p,q,r,s,…表示命题。
探究新知,巩固练习
★★ 1.3.1 且 (and)
下列命题中,命题间有什么关系?
(1)12能被3整除;
(2)12能被4整除;
(3)12能被3整除且能被4整除;
1.问题1:
思考:
命题(3)是由命题(1)(2)使用联结词“且”联结得到的新命题.
一般地,用联结词“且”把命题p和命题q联结起来,就得到一个新命题,记作p∧q,读作“p且q”
填空:一般地,我们规定:当p,q都是真命题时,p∧q是 ;当p,q 两个命题中有一个命题是假命题时,p∧q是 .
一句话概括:
全真为真,有假即假.
真命题
假命题
命题p∧q的真假判断方法:
p q p ∧ q
真 真
真 假
假 真
假 假
假
假
假
真
探究:逻辑联结词“且”的含义与集合中学过的哪个概念的意义相同呢?
对“且”的理解,可联想到集合中“交集”的概念.A∩B={x︱x∈A且x∈B}中的“且”,是指“x∈A”、“x∈B”这两个条件都要满足的意思
活动探究
有些命题如含有“……和……”、“……与……”、“既……,又…..”等词的命题能用“且”改写成“p∧q”的形式,
★★1.3.2 或 (or)
下列命题中,命题 间有什么关系?
(1)27是7的倍数;
(2)27是9的倍数;
(3)27是7的倍数或是9的倍数.
1.问题1:
思考:
命题(3)是由命题(1)(2)使用联结词“或”联结得到的新命题.
一般地,用联结词“或”把命题p和命题q联结起来,就得到一个新命题,记作p∨q,读作“p或q”.
一般地,我们规定:当p,q两个命题中
有 个命题是真命题时,p∨q是 命题;
当p,q两个命题都是假命题时,p∨q
是 命题.
一句话概括:
有真即真, 全假为假.
一
真
假
命题p∨q的真假判断方法:
p q p∨q
真 真
真 假
假 真
假 假
假
真
真
真
探究:逻辑联结词“或”的含义与集合中学过的哪个概念的意义相同呢?
对“或”的理解,可联想到集合中“并集”的概念.A∪B={x︱x∈A或x∈B}中的“或”,它是指
“x∈A”、“x∈B”中至少一个是成立的,即x∈A且
x B;也可以x A且x∈B;也可以x∈A且x∈B.
活动探究
如果p∧q为真命题,那么p∨q一定是真命题吗 反之,如果p∨q为真命题,那么p∧q一定是真命题吗
总结思考
p∧q为真命题 p∨q是真命题
p∨q是真命题 p∧q为真命题
下列两组命题间有什么关系?
(1)35能被5整除;
(2)35不能被5整除.
(3)方程 x2+x+1=0有实数根;
(4)方程 x2+x+1=0无实数根
★★1.3.3 非 (not)
一般地,对一个命题p全盘否定,就得到一个新命题,记作 p,读作“非p”或“p的否定”.
命题(2)是命题(1)的否定,命题(4)是命题(3)的否定.
思考:
1.问题1
填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考:命题P与┐p的真假关系如何?
一句话概括:
真假相反
p与┐p真假性相反
真命题
假命题
p p
真
假
假
真
对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.
探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?
活动探究
探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?
命题的否定与否命题是完全不同的概念
(1)原命题“若P则q” 的形式,它的非命题“若p,则 q”;而它的否命题为 “若┓p,则┓q”.
(2)命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.
命题的否定与否命题的区别
例:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:
正方形的四条边不相等.
若一个四边形不是正方形,则它的四条边不相等.
原词语 否定词 原词语 否定词
等于 任意的
是 至少有一个
都是 至多有一个
大于 至少有n个
小于 至多有n个
一些常见的结论的否定形式
不是
不都是
不大于
大于或等于
一个也没有
至少有两个
至多有(n-1)个
至少有(n+1)个
不等于
某个
“或”的否定是“且”
p q 非p p且q p或q
真 真 假 真 真
真 假 假 假 真
假 真 真 假 真
假 假 真 假 假
真值表:
非p 真假相反
p且q 一假必假
p或q 一真必真
“或”:不等式 x2 x 6>0的解集{ x | x< 2或x>3 }
“且”:不等式 x2 x 6<0的解集 { x | 2< x<3 }
即 { x | x> 2且x<3 }
“非”:三角形的内角和不大于180°
“或” A∪B={x|x∈A或x∈B}
“且” A∩B={x|x∈A且x∈B}
“非” UA={x|x∈U且x A}
“或”、“且”、“非”与集合的意义相同吗
拓展延伸
例1、设p:方程x2+mx+1=0有两个不等的负根,q:方程4x2+4(m-2)x+1=0无实根.若p∨q为真,p∧q为假,求m的取值范围.
解:若方程x2+mx+1=0有两个不等的负根
即 p: m>2
若方程4x2+4(m-2)x+1=0无实根
则 =16(m-2)2-16<0,
即1
∴q:1< m<3
∵p或q为真,则p,q至少一个为真,又p且q为假,则p,q至少一个为假
∴p,q一真一假,p真q假或者p假q真
例2、已知命题 二次函数 在 上是增函数;命题 指数函数
在定义域内是增函数;
命题“ ”为假,且“ ”为假,
求实数 的取值范围.
解:若 为真,则
若 为真,则
由题意可知 真 假,
∵ 是 的必要不充分条件,
∴ 是 的必要不充分条件,
∴ 是 的充分不必要条件.
解:命题 等价于:
例4、设命题p:函数f(x)=lg(ax2-x+ )的定义域为R;命题q:关于x的不等式3x-9x
若命题p为真命题,
当a=0时,-x>0,不合题意;
解答
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
由x>0,得3x>1,∴y=3x-9x的值域为(-∞,0).
若命题q为真命题,则a≥0.
由命题“p或q”为真命题,且“p且q”为假命题,得命题p,q一真一假.
当p真q假时,a不存在;当p假q真时,0≤a≤2.
∴满足条件的a的取值范围是{a|0≤a≤2}.
解答
例5、已知命题p:函数f(x)=(x+m)(x+4)为偶函数;命题q:方程x2+(2m-1)x+4-2m=0的一个根大于2,一个根小于2,若p∧q为假,p∨q为真,求实数m的取值范围.
若命题p为真,则由f(x)=x2+(m+4)x+4m,得m+4=0,解得m=-4.
设g(x)=x2+(2m-1)x+4-2m,其图象开口向上,
若命题q为真,则g(2)<0,即22+(2m-1)×2+4-2m<0,解得m<-3.
由p∧q为假,p∨q为真,得p假q真或p真q假.
若p假q真,则m<-3且m≠-4;
若p真q假,则m无解.
所以m的取值范围为(-∞,-4)∪(-4,-3).
解答
例6、.在一次模拟射击游戏中,小李连续射击了两次,设命题p:“第一次射击中靶”,命题q:“第二次射击中靶”,试用p、q及逻辑联结词“或”、“且”、“非”表示下列命题:
(1)两次射击至少有一次中靶;
(2)两次射击一次都没有中靶.
p∨q
(┐p) ()
例7、已知命题p:若,则恒成立;q:的充要条件是则下列命题为真命题的是( )
D
例8、若命题p:,则┐p是( )
A. B.
C. D.
例10、已知命题p:点M(1,2)在不等式表示的区域内;
q:直线与直线相交.若为真命题,则实数m的取值范围.
例9、已知命题[p (┐q)] [(┐p) (┐q)]为真命题,则( )
A. 都为真 B. 都为假 C. D. 真
一个或多个逻辑联结词设计新的真命题!
其中真命题的是( )
C
甲,乙,丙三位同学中的一位在昨天晚上放学后把教室打扫干净了,今天早上,老师问她们三个人是谁做的好事。
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
已知只有一位同学说的是真话,你们能帮助老师找出是谁做的吗?
趣味情景
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
甲说
的是真话
乙说
的是假话
丙说
的是假话
是我做的
是我做的
是乙做的
矛盾!
丙说
的是真话
甲说
的是假话
乙说
的是假话
不是乙做的
是我做的
不是我做的
矛盾!
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
乙说
的是真话
甲说
的是假话
丙说
的是假话
不是乙做的
是我做的
不是我做的
不矛盾!
甲说:“是乙做的”;
乙说:“不是我做的”;
丙说:“不是我做的”。
