03逻辑门真值表转换成表达式 课件-2022届高三苏教版通用技术一轮专题复习(共11张PPT)
文档属性
| 名称 | 03逻辑门真值表转换成表达式 课件-2022届高三苏教版通用技术一轮专题复习(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 53.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 通用技术 | ||
| 更新时间 | 2022-06-21 23:37:03 | ||
图片预览




文档简介
(共11张PPT)
真值表转换成逻辑门表达式的
方法讲解
方法一:公式法
适用情景:
二输入4种情况或三输入的8种情况都是明确的。
这样的情景下,直接用公式法,可以非常精准做出来,又快又对。
万能公式Ⅰ
F= ABC+ABC+……+ABC
真值表中有n行是F=1,则该式中就有n个(ABC) 以“或门”形式结合,每一个ABC代表每一行真值的信号,若输入信号出现0,则对应输入信号上加个“非门”,否则不需要加。
写完该表达式进行化简即可得到最简表达。
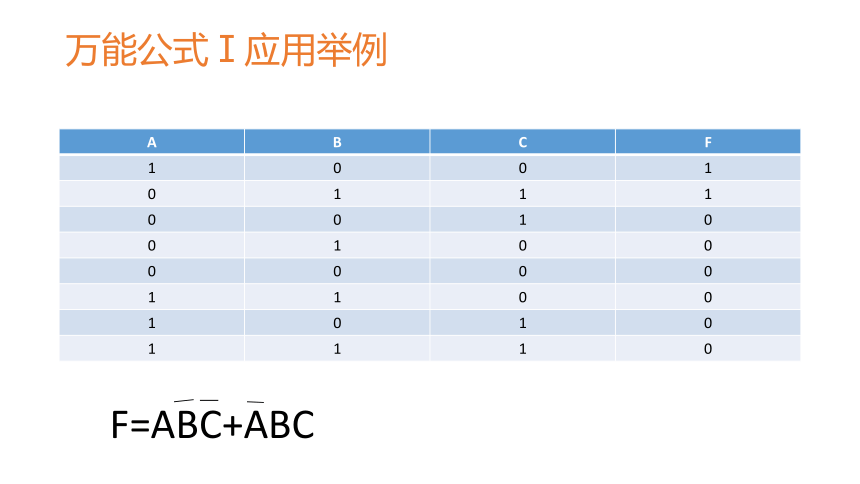
万能公式Ⅰ应用举例
A B C F
1 0 0 1
0 1 1 1
0 0 1 0
0 1 0 0
0 0 0 0
1 1 0 0
1 0 1 0
1 1 1 0
F=ABC+ABC
万能公式Ⅱ
F=(A+B+C)×(A+B+C)×……+(A+B+C)
真值表中有n行是F=0,则该式中就有n个(A+B+C) 以“与门”形式结合,每一个ABC代表每一行真值的信号,若输入信号出现1,则对应输入信号上加个“非门”,否则不需要加。
写完该表达式进行化简即可得到最简表达。
万能公式Ⅱ应用举例
A B C F
1 0 0 0
0 1 1 0
0 0 1 1
0 1 0 1
0 0 0 1
1 1 0 1
1 0 1 1
1 1 1 1
F=(A+B+C)×(A+B+C)
公式法的衍生应用
A B C F 非F
1 0 0 0 1
0 1 1 0 1
0 0 1 1 0
0 1 0 1 0
0 0 0 1 0
1 1 0 1 0
1 0 1 1 0
1 1 1 1 0
F=ABC+ABC
F=F=ABC+ABC
方法二:三信号中找二信号法
适用情景:
本方法适用于三输入信号的8个情况没有完全枚举出来,题干又要求使用最简的表达式,而输出信号正好可以和其中两个输入信号构成逻辑,此时考虑用此法。
方法二的应用举例
A B C F
0 1 1 1
0 1 0 0
1 1 1 0
1 0 0 0
0 1 0 0
1 1 0 0
以上经观察发现,第一行和第二行比较,ABF构不成逻辑,第一行和第三行比较,BCF构不成逻辑,而ACF能构成逻辑。再观察只有A=0 C=1 F才输出1,其余都为0.所以F=AC
方法三:公式雏形法
在方法二的使用过程中,发现三输入信号中任意两种信号都无法和输出信号构成逻辑,而题干又要求最简表达,或者要求指定个数的逻辑门使用,那么则考虑用公式雏形法,先通过观察,写出雏形公式,比如
若A=0 F=0 就写F=A×( )
若A=1 F=1 就写F=A+( )
若A=0 F=1 就写F=A+( )
若A=1 F=0 就写F=A×( )
方法三的应用举例
A B C F
0 0 0 0
0 0 1 1
0 1 1 0
1 1 1 1
如上图所示,经观察,任意两个输入信号都无法和输出信号构成逻辑,所以选用方法三,这里再次观察可得到,当A=1 F=1,所以可以写出F=A+( ),再根据第二行可用万能公式写出F=A+B×C
当然也有人发现,当C=0 F=0,所以可以写出F=C×( ),再根据第三行可用万能公式写出
F=C×(A+B)
以上两个表达式都正确,再根据题目所提供的逻辑门选择较简洁的表达式
真值表转换成逻辑门表达式的
方法讲解
方法一:公式法
适用情景:
二输入4种情况或三输入的8种情况都是明确的。
这样的情景下,直接用公式法,可以非常精准做出来,又快又对。
万能公式Ⅰ
F= ABC+ABC+……+ABC
真值表中有n行是F=1,则该式中就有n个(ABC) 以“或门”形式结合,每一个ABC代表每一行真值的信号,若输入信号出现0,则对应输入信号上加个“非门”,否则不需要加。
写完该表达式进行化简即可得到最简表达。
万能公式Ⅰ应用举例
A B C F
1 0 0 1
0 1 1 1
0 0 1 0
0 1 0 0
0 0 0 0
1 1 0 0
1 0 1 0
1 1 1 0
F=ABC+ABC
万能公式Ⅱ
F=(A+B+C)×(A+B+C)×……+(A+B+C)
真值表中有n行是F=0,则该式中就有n个(A+B+C) 以“与门”形式结合,每一个ABC代表每一行真值的信号,若输入信号出现1,则对应输入信号上加个“非门”,否则不需要加。
写完该表达式进行化简即可得到最简表达。
万能公式Ⅱ应用举例
A B C F
1 0 0 0
0 1 1 0
0 0 1 1
0 1 0 1
0 0 0 1
1 1 0 1
1 0 1 1
1 1 1 1
F=(A+B+C)×(A+B+C)
公式法的衍生应用
A B C F 非F
1 0 0 0 1
0 1 1 0 1
0 0 1 1 0
0 1 0 1 0
0 0 0 1 0
1 1 0 1 0
1 0 1 1 0
1 1 1 1 0
F=ABC+ABC
F=F=ABC+ABC
方法二:三信号中找二信号法
适用情景:
本方法适用于三输入信号的8个情况没有完全枚举出来,题干又要求使用最简的表达式,而输出信号正好可以和其中两个输入信号构成逻辑,此时考虑用此法。
方法二的应用举例
A B C F
0 1 1 1
0 1 0 0
1 1 1 0
1 0 0 0
0 1 0 0
1 1 0 0
以上经观察发现,第一行和第二行比较,ABF构不成逻辑,第一行和第三行比较,BCF构不成逻辑,而ACF能构成逻辑。再观察只有A=0 C=1 F才输出1,其余都为0.所以F=AC
方法三:公式雏形法
在方法二的使用过程中,发现三输入信号中任意两种信号都无法和输出信号构成逻辑,而题干又要求最简表达,或者要求指定个数的逻辑门使用,那么则考虑用公式雏形法,先通过观察,写出雏形公式,比如
若A=0 F=0 就写F=A×( )
若A=1 F=1 就写F=A+( )
若A=0 F=1 就写F=A+( )
若A=1 F=0 就写F=A×( )
方法三的应用举例
A B C F
0 0 0 0
0 0 1 1
0 1 1 0
1 1 1 1
如上图所示,经观察,任意两个输入信号都无法和输出信号构成逻辑,所以选用方法三,这里再次观察可得到,当A=1 F=1,所以可以写出F=A+( ),再根据第二行可用万能公式写出F=A+B×C
当然也有人发现,当C=0 F=0,所以可以写出F=C×( ),再根据第三行可用万能公式写出
F=C×(A+B)
以上两个表达式都正确,再根据题目所提供的逻辑门选择较简洁的表达式
同课章节目录
