勾股定理与平方根整章导学案
图片预览


文档简介
盐城市鞍湖实验学校八年级数学导学案 《勾股定理与平方根》
2.1勾股定理(1)
班级 姓名
【学习目标】
1. 能说出勾股定理,并能应用勾股定理解决简单的问题。
2. 探索勾股定理的过程,发展合情推理的能力,体会数型结合的思想。
【学习重、难点】勾股定理的内容。应用勾股定理解决简单的问题。
一、课前导学
1. 直角三角形边、角有哪些性质?
2. 求下列图中表示边的未知数x、y、z的值. (课本45页练习第2题)
3. 湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )
A.5千米 B.12千米 C.10千米 D.13千米
二、合作探究
活动一:观察分析这枚邮票的图案,你有哪些发现?
活动二:探究实验
1、小方格的面积看作1,以BC为一边的正方形的面积是16,以AC为一边的正方形的面积是9,你能计算出以AB为一边的正方形的面积吗?"
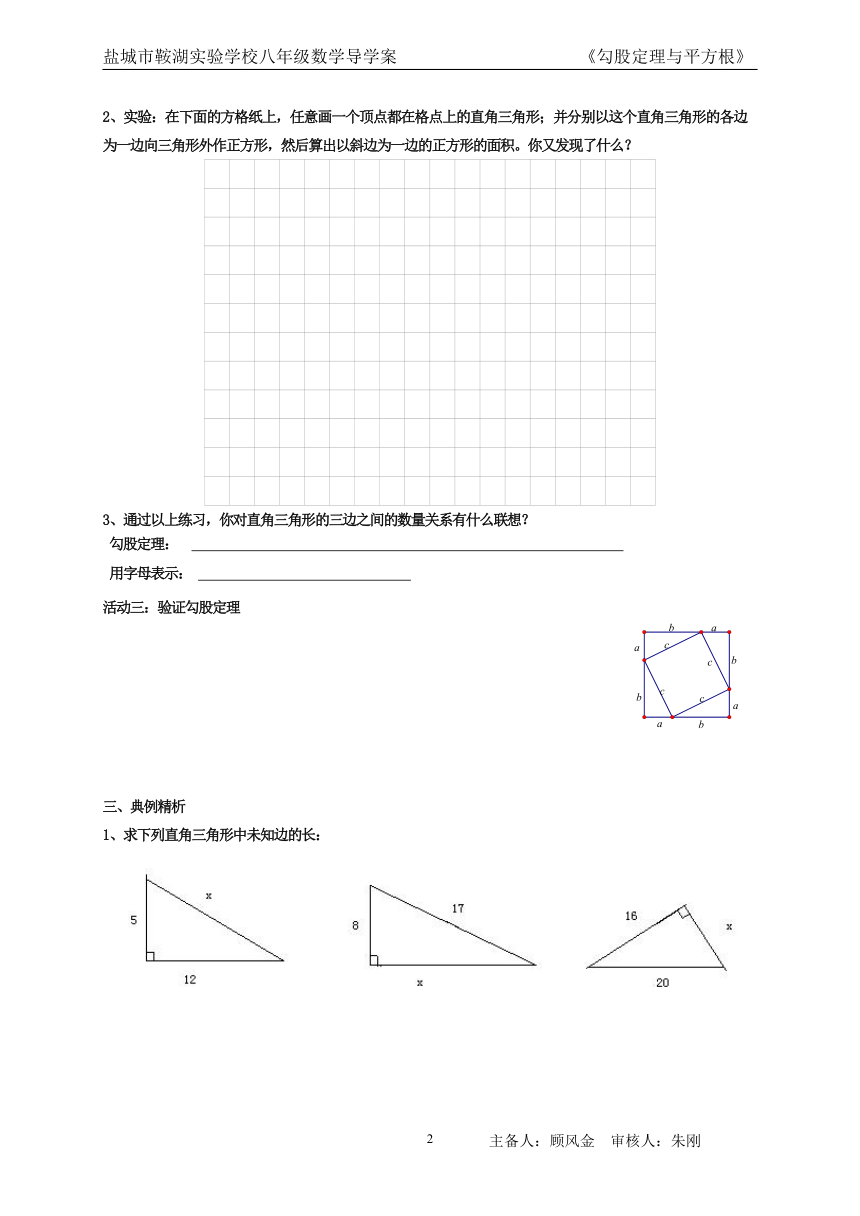
2、实验:在下面的方格纸上,任意画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,然后算出以斜边为一边的正方形的面积。你又发现了什么?
3、通过以上练习,你对直角三角形的三边之间的数量关系有什么联想?
勾股定理:
用字母表示:
活动三:验证勾股定理
三、典例精析
1、求下列直角三角形中未知边的长:
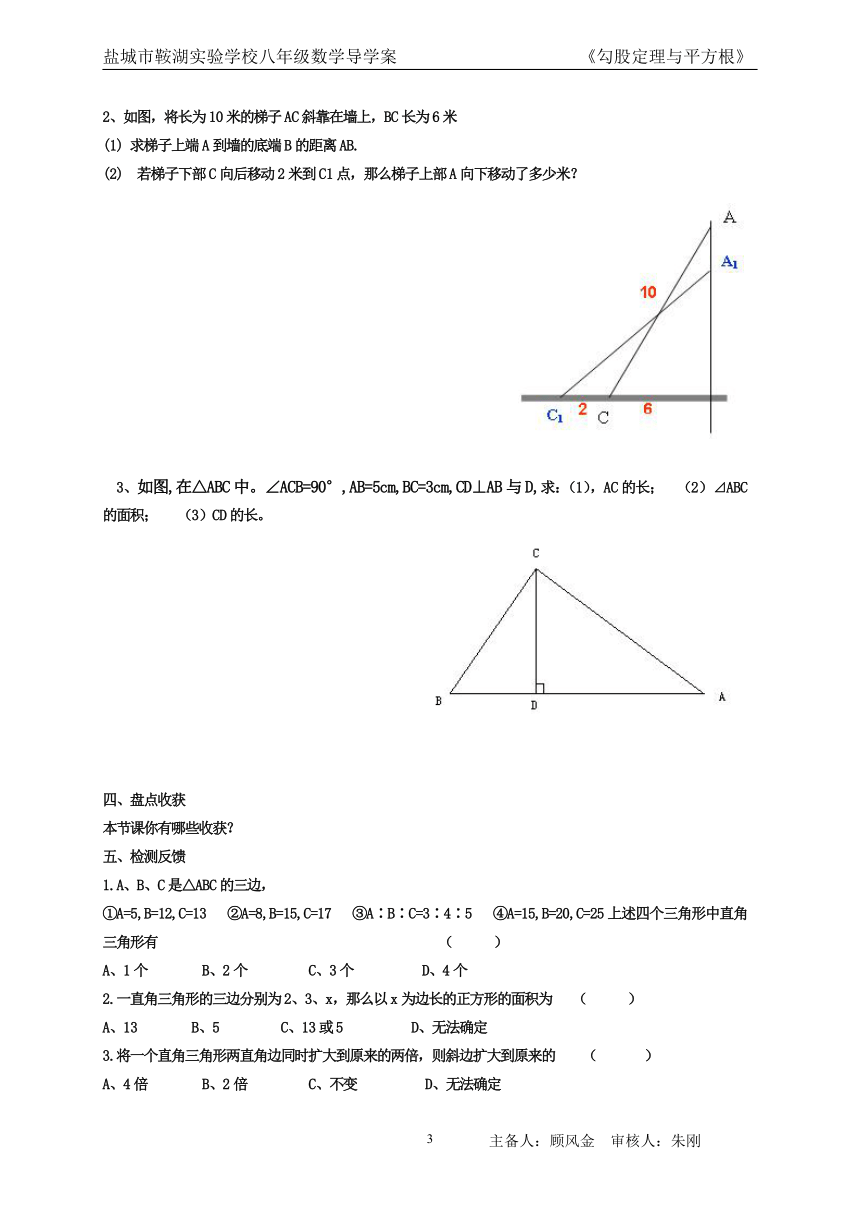
2、如图,将长为10米的梯子AC斜靠在墙上,BC长为6米
(1) 求梯子上端A到墙的底端B的距离AB.
(2) 若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
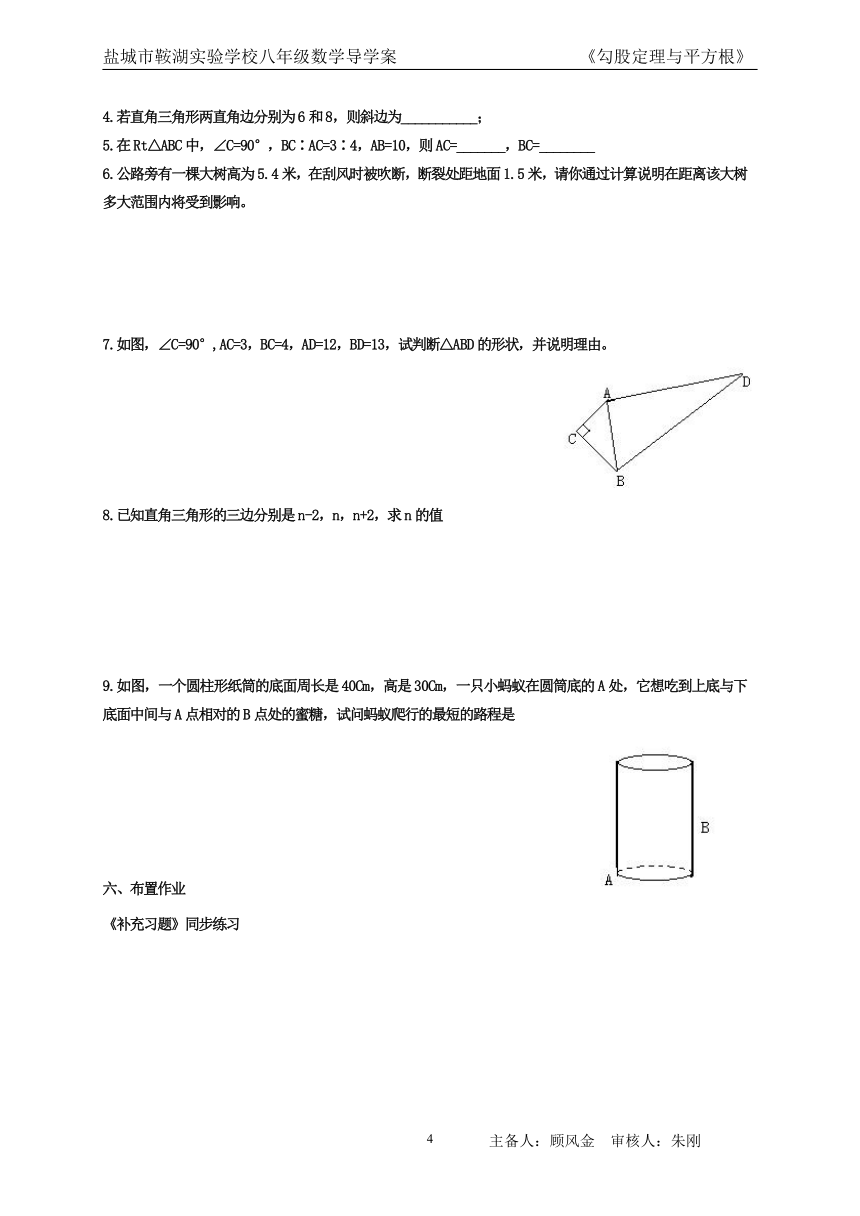
3、如图,在△ABC中。∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB与D,求:(1),AC的长; (2)⊿ABC的面积; (3)CD的长。
四、盘点收获
本节课你有哪些收获?
五、检测反馈
1.A、B、C是△ABC的三边,
①A=5,B=12,C=13 ②A=8,B=15,C=17 ③A∶B∶C=3∶4∶5 ④A=15,B=20,C=25上述四个三角形中直角三角形有 ( )
A、1个 B、2个 C、3个 D、4个
2.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A、13 B、5 C、13或5 D、无法确定
3.将一个直角三角形两直角边同时扩大到原来的两倍,则斜边扩大到原来的 ( )
A、4倍 B、2倍 C、不变 D、无法确定
4.若直角三角形两直角边分别为6和8,则斜边为 ___________;
5.在Rt△ABC中,∠C=90°,BC∶AC=3∶4,AB=10,则AC=_______,BC=________
6.公路旁有一棵大树高为5.4米,在刮风时被吹断,断裂处距地面1.5米,请你通过计算说明在距离该大树多大范围内将受到影响。
7.如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由。
8.已知直角三角形的三边分别是n-2,n,n+2,求n的值
9.如图,一个圆柱形纸筒的底面周长是40Cm,高是30Cm,一只小蚂蚁在圆筒底的A处,它想吃到上底与下底面中间与A点相对的B点处的蜜糖,试问蚂蚁爬行的最短的路程是
六、布置作业
《补充习题》同步练习
2.1勾股定理(2)
班级 姓名
【学习目标】
1.通过拼图,用面积的方法说明勾股定理的正确性.
2.通过实例应用勾股定理,培养学生的知识应用技能.
【学习重、难点】
1. 用面积的方法说明勾股定理的正确.
2. 勾股定理的应用.
一、课前导学
1、阅读课本第46页到第47页,完成下列问题:
(1)我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦。图(1)称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。图(2)是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就. 你能用不同方法表示大正方形的面积吗
2、剪四个完全相同的直角三角形,然后将它们拼成如图所示的图形。大正方形的面积可以表示为_______,又可以表示为____________.对比两种表示方法,看看能不能得到勾股定理的结论。用上面得到的完全相同的四个直角三角形,还可以拼成如下图所示的图形,与上面的方法类似,也能说明勾股定理是正确的(请逐一说明)。
归纳其共有的证明思路:利用图形的割补,借助前后的面积相等形成关于三边的数量关系。
二、合作探究:
(一)思索、交流:
拼图填空:剪裁出若干个大小、形状完全相同的直角三角形,三边长分别记为a、b、c,如图①.(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和__________ (填“大于”、“小于”或“等于”)图③中小正方形的面积,用关系式表示为________ .(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有__________个正方形,它们的面积之间的关系是________ ,用关系式表示为_____ .(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是_____ _____ ,用关系式表示________ _______ .
(二)应用、探究:
1、如图 ,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
2.如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km,现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20000元/千米,请你在CD选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用F。
三、展示交流
1、如图,64、400分别为所在正方形的面积,则图中字
母A所代表的正方形面积是 _________ 。
2、直角三角形两条直角边的长分别为5、12,则斜边上的高为 。
3、已知甲往东走了4km,乙往南走了3km,这时甲、乙两人相距 。
4、一个长方形的长为12cm,对角线长为13cm,则该长方形的周长为 。
5、以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= 。
6、假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走了3千米,再折向北走了6千米处往东一拐,仅走了1千米就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
四、盘点收获
本节课我们进一步认识了勾股定理,并用两种方法证明了这个定理,在应用此定理解决问题时,应注意只有直角三角形的三边才有这样的关系,如果不是直角三角形应该构造直角三角形来解决。
五、检测反馈
1、填空
在RtΔABC中,∠C=900.
①若a=6,c=10 ,则b=____.
②若a:b=3:4,c=10,则a=____,b=____.
③若a=6,b=8,则斜边c上的高h=______.
2、选择:
①若直角三角形的三边为6、8、x,则x的长为 ( )
A.6 B.8 C.10 D.以上答案均不对
②如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离为 ( )
A.1 B.3 C.4 D.5
③如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为 ( )
A.3 B.4 C.5 D.6
3、①如图3,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,则正方形A、B、C、D的面积之和是______。
②如图4,小方格的面积为1,找出图中以格点为端点且长度为5的线段。
3解答题
1、如图 ,以ΔABC的三边为直径的3个半圆的面积有什么关系 请你说明理由。
2、如图,正方形ABCD的边长为6,F是DC边上的一点,且DF∶FC=1∶2,E为BC的中点,连结AE、AF、EF。
(1)求△AEF的周长;(2)求△AEF的面积
3、 P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
六、布置作业
《补充习题》同步练习
2.2神秘的数组
班级 姓名
【学习目标】
1.会阐述直角三角形的判定条件(勾股定理的逆定理)
2.会应用直角三角形的判定条件判定一个三角形是直角三角形
3.经历探索一个三角形是直角三角形的条件的过程,发展合情推理能力,体会“形”与“数”的内在联系。
【学习重、难 点】1利用“三角形的三边a、b、c满足a2+b2=c2,那么这个三角形是直角三角形“这一条件进行直角三角形的判定
2了解勾股数的由来,并能用直角三角形的判定条件解决一些简单的实际问题
一、课前导学
阅读课本第48页到49页,完成下列问题:
1.请画一个三边分别为3cm,4cm,5cm的三角形,你有什么发现?
2.古巴比伦泥板上的数组揭示了什么奥秘?
3.请你画出两个三角形三边的长分别为6cm,8cm,10cm和5cm,12cm,13cm.你发现它们有什么共同的特点吗?
猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?
二.合作探究
活动一:情境创设
1.古巴比伦泥板:美国哥伦比亚大学图书馆收藏着一块编号为“普林顿“322” (plinmpton322)的古巴比伦泥板,上面密密麻麻的写着什么呢? 泥板上的一些神秘符号实际上是一些数组,你知道这些数组揭示什么奥秘吗?
2.我们学过的直角三角形的判定方法有哪些?
活动二:合作交流
1、请你以3cm、4cm、5cm为三条边画三角形,再用量角器量出这个三角形各角的度数,与你的小组同学交流一下,你发现了什么?再以6cm、8cm、10cm呢?这些三角形的三边之间有什么关系?请把你的发现用自己的语言表达出来。
猜想:三角形的三边之间满足怎样数量关系时,此三角形是直角三角形?
如果三角形的三边长a、b、c满足 ,那么这个三角形是 .
用符号表示∵ ∴
这个结论与勾股定理有什么关系?
我们还把满足a2+b2=c2的三个正整数a,b,c称为勾股数,例如,3,4,5;6,8,10; 5,12,13这3组都是勾股数
2.你能猜想这些神秘的数组揭示什么奥秘了吗?请你验证你的猜想。
三、典例精析
例1 下列各组数是勾股数吗 为什么
(1) 12,15,18; (2)7,24,25 ;
(3) 15,36,39; (4)12,35,36.
例2: 3,4,5 是一组勾股数,如果将这三个数分别扩大2倍,所得的3个数还是勾股数吗 扩大3倍,4倍,n倍呢 为什么
例3:一个零件的形状如图,按规定这个零件中∠A 与∠DBC都应为直角,工人师傅量得零件各边尺寸:AD = 4,AB = 3, DC = 13 , BC=12,你能根据所给的数据说明这个零件是否符合要求吗?
四、盘点收获
1、这节课你学到了什么?
2、在学习过程中你还存在哪些问题?
五、检测反馈
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是 ( )
A. a+b=c B. a:b:c=3:4:5 C. a=b=2c D. ∠A=∠B=∠C
2.若三角形三边长分别是6,8,10,则它最长边上的高为 ( )
A. 6 B. 4.8 C. 2.4 D. 8
3.把三边分别BC=3,AC=4,AB=5的三角形沿最长边AB翻折成△ABC ,则CC 的长为 ( )
A. B. C. D.
4.在△ABC中,AB=13,AC=15,高AD=12,则BC的长为 ( )
A. 14 B. 4 C.14或4 D.以上都不对
5、下列各数组中,不能作为直角三角形的三边长的是( )
A、3,4,5 B、10,6,8 C、4,5,6 D、12,13,5
6、若△ABC的两边长为8和15,则能使△ABC为直角三角形的第三边的平方是( )
A、161 B、289 C、17 D、161或289
7、4个三角形的边长分别为:①a=5,b=12,c=13;②a=2,b=3,c=4; ③a=2.5,b=6,c=6.5; ④a=21,b=20,c=29.
其中,直角三角形的个数是( )
A、4 B、3 C、2 D、1
8. 在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_______ .
9. 已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是______ 三角形.
10 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角
边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= .
11.若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
12.如图,在四边形ABCD中,已知:AB=1,BC=2,CD=2,AD=3,且AB⊥BC.试说明AC⊥CD的理由.
13. 已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求图形的面积.
14. 欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请说明理由.
15、如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30cm,DC=12cm,AB=3cm,BC=4cm,求△ABC的面积。
16.要做一个如图所示的零件,按规定∠B与∠D都应为直角,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗?
17.如图,已知AD是BC边上的中线,如果BC=10㎝,AC=4㎝,AD=3㎝,求△ABC的面积。
六、布置作业
《补充习题》同步练习
2.3 平方根(1)
班级 姓名
【学习目标】了解数的平方根的概念.会用根号表示一个数的平方根。
了解开平方与乘方是互逆的运算,会求非负数的平方根。
【学习重、难点】一个数的平方根的概念理解及表示方法
一、课前导学
1.一个数的平方等于它本身,这个数是 。一个数的平方根等于它本身,这个数是 。
2.若3a+1没有平方根,那么a一定 。
3.若4a+1的平方根是±5,则a= 。
4.一个数x的平方根等于m+1和m-3,则m= 。x= 。
5.若|a-9|+(b-4) =0,则 ab的平方根是 。
6. 求下列各式中的x:
(1) x =16 (2) x =9 (3) x =15 (4) 4x =81
二、合作探究
活动一:设图中小方格的边长为1,你能分别说出图中两个长方形的对角线AB、A′B ′的长吗?
活动二:交流 如果一个数的平方等于9,这个数是几? 一个数的平方等于2呢?
活动三:引出概念、掌握表示方法
例如:2 =4,(-2) =4,±2叫做4的平方根。
10 =100,(-10) =100,±10叫做100的平方根
13 =169,(--13) =169,±13叫做169的平方根。
一般地,如果一个数的平方等于a,那么这个数叫做a的 ,也称为 。
也就是说,如果 ,那么 叫做 的平方根。
表示方法:一个正数的平方根有 个,它们互为 。一个正数a的正的平方根,记作“ ” 一个正数a的负的平方根记作“- ”,这两个平方根合起来记作“± ”,读作“正负根号a”。
例如,2的平方根记作“± ”,读作“正负根号2”。81的平方根记作“± ”,读作“正负根号81”
活动四:尝试交流、引出结论
1.9的平方根是什么?25的平方根是什么?
2.0的平方根是什么?0的平方根有几个?
3.-4、-8、-36有平方根吗?为什么?
结论:
求一个数a的平方根的运算,叫做开平方.
三、典例精析
例: 求下列各数的平方根:
(1)25; (2)0.81; (3)15; (4)(-2)
四、展示交流
求下列各数的平方根:
81 289 0 2.56
五、盘点收获
本节课你有哪些收获?
六、检测反馈
1.下列说法正确的是( ).
A.的平方根是 B.2是4的平方根
C.任何数的平方是非负数,因而任何数的平方根也是非负数
D.任何一个非负数的平方根都不大于这个数
2.的平方根是( ).
A. B.12 C D.
3.下列各数没有平方根的是( ).
A.18 B. C. D.11.1
4.如果有意义,则x可以取的最小整数为( ).
A.0 B.1 C.2 D.3
5.的值是( ).
A. B.3 C. D.9
6.下列说法不正确的是( ).
A.表示两个数:或 B.的指数是2
C.在数轴上表示正数的两个平方根的两个点,总是关于原点对称
D.正数的两个平方根的积为负数
7.若,则x+y的值是( ).
A.-2 B.-3 C.-4 D.无法确定
8.一个数如果有两个平方根,那么这两个平方根的和是( ).
A.大于0 B..等于0 C.小于0 D.大于或等于0
9.若a≥0,则4a2的平方根是( ).
A.2a B.±2a C. D.∣2a∣
10.25的平方根记作 ,结果是 .
11.361的平方根是 ,
12.(-4)2的平方根是 。
13.-9是数a的一个平方根,那么数a的另一个平方根是 ,数a是 。
14.若,则y= .
15.求下列各式的值:
⑴= ⑵ = ⑶= .
⑷= ⑸= ⑹= .
16.求下列各式中的x.
⑴若x2=49,则x= . ⑵若4(x-1)2=25,则x= .
⑶若9(x2+1)=10,则x= . ⑷若=3,则x= .
17.已知与互为相反数,求(x-y)2的平方根。
18.已知2a-1的平方根是±3,3a+b-1的平方根为±4,求a+2b的平方根。
19.如果一个直角三角形的两边长分别是5㎝和12㎝,那么这个三角形的面积是多少?
20.某纸箱加工厂,有一批边长为40㎝的正方形硬纸板,现准备将此纸板折成没盖的纸盒。首先在四个角上截去四个相同的小正方形,然后做成底面积为625㎝2的纸盒子,想一想,你怎样求出截去的小正方形的边长?
七、布置作业
《补充习题》同步练习
2.3 平方根(2)
班级 姓名
【学习目标】了解数的算术平方根的概念.会用根号表示一个数的算术平方根。
能运用算术平方根解决实际问题。
【学习重、难点】根据一个数的算术平方根的意义解决有关问题。
一、课前导学
1.正数a有 个平方根,其中正数a的正的平方根,也叫做a的 。
例如:4的平方根是 ,其中 叫做4的算术平方根,记作 ,
2的平方根是 ,其中 叫做2的算术平方根,
0只有一个平方根,0的平方根也叫做0的算术平方根,即 =0
2.面积为15m2正方形的边长是多少?
二、交流合作
活动一:组内交流
1. 16的算术平方根的平方根是什么? 5的算术平方根是什么?
2、 0的算术平方根是什么?0的算术平方根有几个?
3、 -2、-5、-6有算术平方根吗?为什么?
活动二:讨论
1.等于多少?呢?
2. 等于多少?等于多少?等于多少
三、典例精析
例1:求下列各数的算术平方根:
(1)625; (2)0.81; (3)6; (4)(-2)
例2:“欲穷千里目,更上一层楼”。说的是登的高看得远。若观测点的高度为h,观测者视线能达到的最远距离为d≈ ,其中R是地球半径(通常取6400km),小丽站在海边一块岩石上,眼睛离地面的高度为20M,她观测到远处一艘船刚露出海平面,此时该小船离小丽有多远?
四、展示交流
1.一个数的算术平方根等于它本身,这个数是 。
2.若x =16,则5-x的算术平方根是 。
3.若4a+1的平方根是±5,则a 的算术平方根是 。
4.16的平方根等于 ,算术平方根等于 。
5.在△ABC中,∠C=90°.(1)如果AC=5,BC=12,求AB;(2)如果AC=2,BC=1,求AB;(3)如果AB=25,BC=24,求AC;(4)如果AC=5,AB=12,求BC;
五、盘点收获
平方根与算术平方根的区别与联系
六、检测反馈
1.下列语句正确的是( )
A.一个数的平方根一定是两个数 B.一个非负数的非负平方根一定是它的算术平方根
C.一个正数的平方根一定是它的算术平方根 D.一个非零的正的平方根是它的算术平方根
2.若有意义,则a能取的最小整数为( ).
A.0 B.1 C.-1 D.-4
3.若,则x+y的值是( ).
A.-2 B.-3 C.-4 D.无法确定
4.一个数的算术平方根只要存在,那么这个算术平方根( ).
A.只有一个,并且是正数 B.不可能等于零 C.一定小于这个数 D.必定是非负数
5.若a是有理数,下列说法正确的是( ).
A. a2的算术平方根是a B. a2的平方根是a
C. a2的算术平方根是∣a∣ D. a2的平方根是∣a∣
6.一个数如果有两个平方根,那么这两个平方根发和是( ).
A.大于0 B..等于0 C.小于0 D.大于或等于0
7.若a≥0,则4a2的算术平方根是( ).
A.2a B.±2a C. D.∣2a∣
8.的算术平方根是( ).
A.4 B.±4 C.2 D.±2
9.(-4)2的算术平方根是 36的倒数的算术平方根的相反数是________.
10.的最小值是________,此时a的取值是________.
11.的算术平方根是2,x=________.
12.已知正数a和b,有下列命题:(1)若,则≤(2)若,则≤
(3)若,则≤ 根据以上三个命题所提供的规律猜想:若,则≤________.
13.一个正数的两个平方根的和是________.
14.一个正数的两个平方根的商是________.
15.如果,那么x=________;如果,那么________.
16.当时,________.
17.一个数的平方根等于它本身,那么这个数是________.
18.计算:
19.求下列各式中x的值.
20.下列各式中,哪些有意义?
(1) (2) (3) (4) (5)
21.已知的平方根是,的平方根是,求的平方根.
22.如图所示,已知正方形ABCD的面积是49平方厘米,正方形EFGH的面积是25平方厘米,且AH=DG=CF=BE,BF=CG=DH=AE,求AD的长;EF的长;△AEH的面积.
七、布置作业
《补充习题》同步练习
2.4 立方根
班级 姓名
【学习目标】
1. 在一定的情境只,理解立方根的概念,使学生不断获得解决问题的经验,提高思维水平,学习中要注意感悟"类比"在知识产生和发展过程中的作用。
2. 了解立方根的概念,会用根号表示一个数的立方根,了解开立方与立方互为逆运算,能用立方运算求一些数的立方根
3. 能用立方根解决一些简单的实际问题。
【学习重、难点】正确地理解立方根的概念及符号表示并能熟练应用
一、课前导学
(1)1的立方根是________,-1的立方根是________,0的立方根是________.
(2)求下列各数的立方根:
(1)-; (2)-(-0.216); (3)10-3.
二、合作探究
活动一:解决以下问题
1. 现有一只体积为216cm3的正方体纸盒,它的每一条棱长是多少?
2.阅读课本第55页到56页。完成下列问题:
①观察思考:如图,棱长为1时,正方体的体积是13=1,设体积为2的正方体的棱长为x.依题意列方程得: .
②体积为1的正方体,棱长为多少?体积增加1,棱长为多少?
③做一个正方体纸盒,使它的容积为64cm,正方体纸盒的棱长是多少?如果要使正方体纸盒容积为25cm,它的棱长是多少?
活动二:归纳概念
定义:1、一般地,如果一个数的立方等于a,这个数就叫做a的 ,也称为 .也就是说,如果x3=a,那么x叫做a的 ,数的立方根记作 ,读作
例如:4的立方是 所以4是64的立方根,记作 ,又如,x是2的立方根,记作
2、求一个数的立方根的运算叫做
3、立方根的性质:正数有 立方根,负数有 立方根,0的立方根是
三、典例精析
1.求下列各数的立方根
⑴, ⑵ , ⑶0, ⑷
2.求下列各式的值⑴,⑵,⑶,⑷
3.求下列各式中的x
x+729=0 (x-3)=64
四、盘点收获
⑴掌握立方根的定义和性质;⑵会求一个数的立方根;⑶理解并掌握公式
五、检测反馈
1、立方根等于本身的数是 ( )
A、±1 B、1,0 C、±1,0 D、以上都不对
2、若一个数的算术平方根等于这个数的立方根,则这个数是( )
A、±1 B、±1,0 C、0 D、0,1
3、下列说法中,错误的是( )
A、64的立方根是4 B、立方根 C、的立方根是2 D、125的立方根是±5
4、下列说法正确的是( )
A、1的立方根与平方根都是1 B、C、的平方根是 D、
5.-6的立方根用符号表示,正确的是( )
A B - C - D
6.下列说法正确的是( )
A、任意数a的平方根有2个,它们互为相反数 B、任意数a的立方根有1个
C、-3是27的负的立方根 D、(-1)的立方根是-1
7.下列判断正确的是( )
A、64的立方根是4 B、(-1)的立方根是1C、的立方根是2 D、如果=a,则a=0
8.(-1)的立方根是 —0.0027的立方根是
9.已知x=64,则=
10.= , =
11. a为何值时,则 , a, , 中,必是非负数的有
12.求下列各数的立方根
⑴,⑵512,⑶—729,⑷
13.求下列各式中的
⑴, ⑵, ⑶
14 .已知一个正方体的棱长是5cm,再做一个正方体,使它的体积等于原正方体的体积的8倍,求要做的正方体的棱长。
六、布置作业
《补充习题》同步练习
2.5 实数(1)
班级 姓名
【学习目标】 1.知道无理数是客观存在的,了解无理数和实数的概念,能对实数按要求进行分类,同时会判断一个数是有理数还是无理数。
2.知道实数和数轴上的点一一对应。
3.经历用有理数估算的探索过程,从中感受“逼近”的数学思想,发展数感,激发学生的探索创新精神。
【学习重、难点】会判断一个数是有理数还是无理数。
一、课前导学
1.实数两种常见的分类形式:
2.把下列各数填入相应的集合之中:
0.456、-、(-)0、3.14、-0.801 08、0、0.101 001 000 1…(每两个1之间依次增加一个0)、、-1.
有理数集合 无理数集合
3.任意写出3个无理数:________________.
二、合作探究
活动一:创设情境
情境一:提出问题—我们通过研究边长为1的正方形的对角线的长为,说说你对的认识。
情境二:现有一个直角三角形,直角边均为1,斜边为多少?你认识这个数吗?
情境三:大家都知道2是一个有理数,它的算术平方根为多少?还是一个有理数吗?
情境四:为了生活的需要人们引入了负数,数就由原来的正数和0扩充为有理数。细心的同学会发现还有一些不是有理数的数,和有理数一起构成了实数,它们到底是什么数呢?
活动二:探索活动
问题1:是有理数吗?
问题2:是一个整数吗?
问题3:是1与2之间的一个分数吗?(也就是1与2之间的分数的平方会等于吗?)
问题4:有多大?
三、例题精析
例:把下列各数填入相应的集合内:
、、0、、、、3.14159、-0.020020002 0.12121121112…
(1)有理数集合{ }
(2)无理数集合{ }
(3)正实数集合{ }
(4)负实数集合{ }
四、展示交流
1.判断正误,若不对,请说明理由,并加以改正。
(1)无理数都是无限小数。 (2)带根号的数不一定是无理数。
(3)无限小数都是无理数。 (4)数轴上的点表示有理数。
(5)不带根号的数一定是有理数。
2. .数、、中,无理数有( ).
(A)0个 (B)1个 (C)2个 (D)3个
3.(1)把下列各数填入相应的集合内:-7,0.32,, ,,- .
有理数集合:{ …};无理数集合:{ …};
无理数集合:{ …}.
五、盘点收获
本节课你有哪些收获?
六、检测反馈
⒈ 在5,0.1,-π,,,,,八个实数中,无理数的个数是 ( )
A.5 B.4 C.3 D.2
⒉ 下列说法中正确的是 ( )
A.有理数和数轴上的点一一对应 B.不带根号的数是有理数
C.无理数就是开方开不尽的数 D.实数与数轴上的点一一对应
⒊ 无理数有 ( )
A.最小的数 B.最大的数 C.绝对值最小的数 D.以上都不对
⒋ 在实数,,3.14,π,,中属于有理数集合的数有 ;属于负实数集合的数有 ;属于无理数集合的数有 .
⒌ 的相反数是 ;倒数是 .
⒍ 点M在数轴上与原点相距个单位,则点M表示的实数为 ,数轴上到的点距离为的点所表示的数是 .
⒎ 已知x,y都是实数,且y=,试求xy的值.
⒏ 若a,b为有理数,且有a,b满足a2+2b+b=17-,求a+b的值.
⒐ 设m是的整数部分,n是的小数部分,试求m-n的值.
⒑ 实数a,b互为相反数,c,d互为倒数,x的绝对值为.
求代数式x2+(a+b+cd)x++的值.
⒒ 如图,在长方形ABCD中,∠DAE=∠CBE=45°,AD=1,求△ABE的面积和周长.
七、布置作业
《补充习题》同步练习
2.5 实数(2)
班级 姓名
【学习目标】
1、了解实数的意义,能对实数按要求进行分类。
2、了解实数范围内,相反数、倒数、绝对值的意义。
3、了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。
【学习重点、难点】了解实数意义,能对实数进行分类,明确数轴上的点与实数一一对应并能用数轴上的点来表示无理数。
一、课前导学
1、判断下列说法是否正确:(1)无限小数都是无理数;(2)无理数都是无限小数; (3)带根号的数都是无理数。
2、求下列各数的相反数、倒数和绝对值:
(1)3.8 (2) (3) (4) (5)
3、在数轴上作出对应的点。
4.实数可分为 与 。
二、合作交流
活动一:在实数概念基础上对实数进行不同分类。
无理数与有理数一样,也有正负之分,如是正的,是负的。
思考:
(1)你能把,,,,,,,,,,0,0.3737737773……(相邻两个3之间7的个数逐次增加1)等各数填入下面相应的集合中?
正有理数:
负有理数:
有理数:
无理数:
(2)0属于正数吗?0属于负数吗?
(3)实数除了可以分为有理数与无理数外,实数还可怎样分?
活动二:了解实数范围内相反数、倒数、绝对值的意义:
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例如,和是互为相反数,和互为倒数。
,,,。
活动三:想一想
1、a是一个实数,它的相反数为 ,绝对值为 ;
2、如果,那么它的倒数为 。
活动四:议一议。
探索用数轴上的点来表示无理数
1.复习勾股定理。如图在Rt△ABC中AB= a,BC = b,AC = c,其中a、b、c满足什么条件。
当a=1,b=1时,c的值是多少?
2.让学生探讨以下问题:
(A)如图OA=OB,数轴上A点对应的数是多少?
(B)如果将所有有理数都标到数轴上,那么数轴上被填满了吗?
三、盘点收获
本节课你有哪些收获?
四、检测反馈
⒈已知0<x<1,那么在x,,,x2中最大的是( )
A.x B. C. D.x2
⒉若实数a,b满足a+b>0,a b<0,则下列不等式中正确的是 ( )
A.|a|>|b| B.当a>0,b<0时,|a|>|b|
C.|a|<|b| D.当a<0,b>0时,|a|>|b|
⒊如图,数轴上表示1,的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为 ( )
A.-1 B.1- C.2- D.-2
⒋ 如果一个实数的绝对值是,那么这个实数是 .
⒌ 若a,b都是无理数,且a+b=2,则a,b的值可以是 (填上一组满足条件的值即可).
⒍ 若|x-|+(y+)2=0,则(x·y)2005= .
⒎ 比较下列各组数的大小:
⑴与 ⑵与 ⑶与
⒏ 计算:
⑴;(保留两位小数)
⑵.(保留两位小数)
⒐ 求下列各式中x的值:
⑴ ; ⑵ .
⒑ 如图,a,b,c是数轴上三个点A、B、C所对应的实数.
试化简:.
11已知实数x满足|x-3|+|x+3|=-2x,试求x的取值范围.
五、布置作业
《补充习题》同步练习
2.6近似数与有效数字
班级 姓名
【学习目标】
1.了解近似数与有效数字的概念,体会近似数的意义及在生活中的作用
2.能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数
【学习重、难点】按要求用四舍五入法取一个数的近似数
一、课前导学
自学教材P62-63页的内容
二、合作交流
活动一:情境创设
李宇春以3528308条短信获得冠军 周笔畅以3270840条短信获得亚军
张靓颖则以1353906条短信获得季军
今年22岁的夏洛特·凯利4年前生出詹尼弗和简孪生姐妹,今年7月30日又生出鲁思和艾米丽两位可爱的孪生小姐妹。艾米丽出生时体重约为8.12磅,鲁思出生时的体重则为约7.20磅。
活动二:认识近似数
实际生产生活中的许多数据都是近似数,例如测量长度,时间,速度所得的结果都是近似数,且由于测量工具不同,其测量的精确程度也不同。在实际计算中对于像π这样的数,也常常需取它们的近似值.请说说生活中应用近似数的例子。
取一个数的近似值有多种方法,四舍五入是最常用的一种方法。用四舍五入法取一个数的近似数时,四舍五入到哪一位,就说这个近似数精确到哪一位.
例如,圆周率=3.1415926…
取π≈3,就是精确到个位(或精确到1)取π≈3.1,就是精确到十分位(或精确到0.1)
取π≈3.14,就是精确到百分位位(或精确到0.01)
取π≈3.142,就是精确到千分位位(或精确到0.001)
活动三:认识有效数字
对一个近似数,从左面第一个不是0的数字起,到末位数字止,所有的数字都称为这个近似数的有效数字。
例如:上面圆周率π的近似值中,3.14有3个有效数字3,1,4;3.142有4个有效数字3,1,4,2.
三、典例精析
例1 小亮用天平称得罐头的质量为2.026kg,,按要求取近似数,并指出每个近似数的有效数字:
(1)精确到0.01kg; (2)精确到0.1kg; (3)精确到1kg.
例2 用四舍五入法,按要求对下列各数取近似值,并用科学记数法表示.
(1) 地球上七大洲的面积约为149480000(保留2个有效数字)
(2) 某人一天饮水1890ml(精确到1000ml)
(3) 小明身高1.595m(保留3个有效数字)
(4) 人的眼睛可以看见的红光的波长为0.000077cm(精确到0.00001)
四、展示交流
1. 教材P63第 1、2题
2 .创新探究
张娟和李敏在讨论问题。
张娟:如果你把7498近似到千位数,你就会得到7000.
李敏:不,我有另外一种解答方法,可以得到不同的答案。首先将7498近似到百位得7500,接着把7500近似到千位,就得到8000。
张娟:……
你怎样评价张娟和李敏的说法呢?
3. 研究性学习练习
有一个四位数x,先将它四舍五入到十位,得到近似数m,再把四位数m四舍五入到百位,得到近似数n,再把四位数n四舍五入到千位,恰好是2000,你能求出四位数x的最大值与最小值吗?
五、盘点收获
本节课你有哪些收获?
六、检测反馈
⒈ 圆周率π=3.1415926…精确到千分位的近似数是 ( )
A.3.14 B.3.141 C.3.142 D.3.1416
⒉ 近似数3.14×104的有效数字有 ( )
A.1个 B.2个 C.3个 D.4个
⒊ 2004年某市完成国内生产总值(GDP)达3466.53亿元,用四舍五入法取近似值,保留3个有效数字,并用科学记数法表示,其结果是 ( )
A.3.47×103亿元 B.3.47×104亿元
C.3.467×103亿元 D.3.467×104亿元
⒋ 对于近似数10.08与0.1008,下列说法正确的是 ( )
A.它们的有效数字与精确位数都不相同 B.它们的有效数字与精确位数相同
C.它们的精确位数不同,有效数字相同 D.它们的有效数字不同,精确位数相同
⒌ 近似数1.69万精确到 位,有 个有效数字,有效数字是 .
⒍ 小明的体重约为51.51千克,如果精确到10千克,其结果为 千克;如果精确到1千克,其结果为 千克;如果精确到0.1千克,其结果为 千克.
⒎ 2003年10月15日9时10分,我国神舟五号载人飞船准确进入预定轨道.16日5时59分,返回舱与推进舱分离,返回地面.其间飞船绕地球共飞行了14圈,飞行的路程约为60万km,则神舟五号载人飞船绕地球平均每圈飞行 km(用科学记数法表示,结果保留3个有效数字).
⒏ 计算:⑴3+-(保留两个有效数字) ⑵(精确到0.01)
⒐ 以下问题中的近似数各精确到哪一位?各有几个有效数字?
⑴我国人口约为13亿人;
⑵π的近似值是3.14;
⑶某厂2004年的产值约为2000万元,约是1998年的6.8倍.
⒑ 用四舍五入法,,按要求对下列各数取近似值,并用科学记数法表示:
⑴太空探测器“先驱者10号”从发射到2003年2月人们收到它最后一次发回的信号时,它已飞离地球12200000000km(保留2个有效数字);
⑵2005年6月5日是世界第34个世界环境日,目前全球海洋总面积约为36105.9万km2(保留3个有效数字);
⑶光年是天文学中的距离单位,1光年大约是9500000000000km;
⑷某市全年的路灯照明用电约需4200万kw·h(精确到百万位).
六、布置作业
《补充习题》同步练习
2.7勾股定理的应用(1)
班级 姓名
【学习目标】
1、能运用勾股定理及直角三角形的判定条件解决实际问题.
2、在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.
【学习重、难点】勾股定理的实际运用;转化思想的过程渗透。
活动一:情境创设 、复习回忆
提出问题:如果知道桥面以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
直角三角形两直角边的平方和等于斜边的平方
a2+b2=c2 AC2+BC2=AB2
活动二:例题教学
例1 南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从C处到B处,如果直接走湖底隧道CB,比绕道CA (约1.36km)和AB (约2.95km)减少多少行程 (精确到0.1km)
活动三:探索活动
一架长为10m的梯子AB斜靠在墙上.
⑴ 若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远
⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m
⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗
活动四:展示交流
1.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
2. 如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m
3. 一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
活动五:盘点收获
我们知道勾股定理揭示了直角三角形的三边之间的数量关系,已知直角三角形中的任意两边就可以依据勾股定理求出第三边.从应用勾股定理解决实际问题中,我们进一步认识到把直角三角形中三边关系“a2+b2=c2”看成一个方程,只要依据问题的条件把它转化为我们会解的方程,就把解实际问题转化为解方程.
活动六:检测反馈
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;④7、8、9,其中能构成直角三角形的有( ).
A.4组 B.3组 C.2组 D.1组
2.等腰三角形底边上高是8,周长为32,则这个等腰三角形的面积为( ).
A.56 B.48 C.40 D.30
3.要从电杆离地面5m处向地面拉一条长为13m的电缆,则地面电缆固定点与电线杆底部的距离应为( ).
A.10m B.11m C.12m D.13m
4.一海轮以24n mile/h的速度从港口A出发向东南方向航行,另一海轮以18n mile/h的速度同时从港口A出发向西南方向航行,离开港口2h后,两海轮之间的距离为( ).
A. 84n mile B. 60n mile C. 48n mile D.36 n mile
5.如图,已知S1、 S2和 S3分别是 RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、 S2和 S3满足关系式为( ).
A. S1< S2 +S3 B. S1= S2+ S3 C. S1> S2+ S3 D. S1= S2 S3
6.现有两根木棒,长度分别为44㎝和55㎝.若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是( ).
A.22㎝ B.33㎝ C.44㎝ D.55㎝
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 ( ).
A.17m B.18m C.25m D.26m
8.等腰三角形ABC的面积为12㎝2,底上的高AD=3㎝,则它的周长为 。
9.轮船在大海中航行,它从A点出发,向正北方向航行20㎞,遇到冰山后,又折向东航行15㎞,则此时轮船与A点的距离为 ㎞。
10.如图,为测湖两岸A、B间的距离,小兰在C点设桩,使△ABC为直角三角形,并测得BC=12m,AC=15m,则A、B两点间的距离是 m。
11.如果梯子的底端离建筑物7m,则25m的消防梯可到达建筑物的高度是 m。
12. 甲、乙两人同时从同一地点出发,甲往东走了4km,乙往南走了6km,这时甲、乙两人相距__________km.
13.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(取3)是( ).
(A)20cm (B)10cm (C)14cm (D)无法确定
14.如图,铁路上A、B两点相距25㎞,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15㎞,CB=10㎞,现在要在铁路AB上修建一个土特产收购站E,使得C、D两村到E站的距离相等,则E站应修建在离A站多少千米处?
15.如图,在四边形ABCD中,AC⊥DC, △ADC的面积为30,DC=12,AB=3,BC=4,求△ABC的面积
【布置作业】
《补充习题》同步练习
2.7勾股定理的应用(2)
班级 姓名
【学习目标】能运用勾股定理及直角三角形的判定条件解决实际问题、构造直角三角形及正确解出此类方程
【学习难点】在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.要善于运用直角三角形三边关系,关键是根据实际情形准确构造出直角三角形。
【学习过程】
活动一:情境创设
这些图形有什么共同特征
活动二:探索活动
问题一 在右图的直角三角形中,利用勾股定理可知 x=,根据已有的知识,你还知道哪些与这个三角形有关的数据信息吗
问题二 你知道与下图的三角形有关的哪些数据信息呢
问题三 如果要知道一个等边三角形的有关信息,你认为至少需要哪些信息 与同学交.
3.例题教学
图1中的x等于多少 图2中的x、y、z等于多少 沿着图2继续画直角三角形,还能得到那些无理数
1)利用图2你们能在数轴上画出表示的点吗 请动手试一试!
2)怎样在数轴上画出表示 的点呢
3)在数轴上表示的点怎样画出
例1 如图,等边三角形ABC的边长是6,求△ABC的面积。
1、如图5,在△ABC中,AB=AC=17,BC=16,求△ABC的面积
2、如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
例2 交流材料
材料1:如图7,在△ABC中,AB=25,BC=7,AC=24,问△ABC是什么三角形?
材料2:如图8,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,求AC.
材料3: 如图9,在△ABC中, AB=15,AD=12,BD=9,AC=13,求△ABC的周长和面积。
议一议:勾股定理与它的逆定理在应用上有什么区别?
试一试:如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状?
活动三:盘点收获
从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系;把研究等腰三角形转化为研究直角三角形,这是研究问题的一种策略.
活动四:检测反馈
1.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=________.
2.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是__________.
3. 在Rt△ABC中,∠ACB=90°,AC=4,BC=3.求Rt△ABC斜边上的高.
4. 已知一个三角形的三边长分别是12cm、16cm、20cm,你能计算出这个三角形的面积吗?
5. 邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km?
6.如图,已知,EB⊥AD于C,EB=FC,AB=CD,说明AF=ED。
7.如图,已知点B、E、C在一条直线上,∠B=∠C=90°,AE=ED,AB=EC,说明△AED是等腰直角三角形。
8.如图,已知∠B=∠C,∠A=90°,AC=BD,说明AB=CD。
9.如图,已知:等腰直角△ABC中,P为斜边BC上的任一点.
求证:PB2+PC2=2PA2 .
10.如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
1 点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;
2 以⑴中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数.
【布置作业】
《补充习题》同步练习
2.8小结与思考
班级 姓名
【学习目标】1回顾勾股定理及其逆定理,利用勾股定理解决生活中的实际问题
2平方根及立方根,能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数,会进行实数的有关计算
【学习难点】勾股定理及其应用,平方根及立方根
【教学过程】
一、知识要点
1.勾股定理:在一个直角三角形中,两直角边的平方和等于斜边的平方。
2.勾股定理的应用:在一个直角三角形中,知道其中的任意两边都可以求第三边。
①c2=a2+b2;②a2=c2-b2;③b2=c2-a2。
3.直角三角形的识别(勾股定理的逆定理):如果三角形的三边长a、b、c满足a2+b2 =c2,那么这个三角形是直角三角形。(这是判定一个三角形是直角三角形的又一种方法)
4.平方根的定义:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根。也称二次方根,也就是说,如果x2=a,那么x就叫做a的平方根。
5.平方根的性质:①一个正数有两个平方根,它们互为相反数;②0的平方根是0,记作;③负数没有平方根。
6.开平方的定义:求一个数a的平方根的运算,叫做开平方。
7.算术平方根的定义:正数a有2个平方根,其中正数a的正的平方根,也叫做a的算术平方根。公式:()2=a (a≥0),=a (a≥0) , =-a(a≤0)。
8.立方根的定义:一般地,如果一个数的立方等于a,这个数就叫做a的立方根,也称为三次方根;也就是说,如果x3=a,那么x叫做a的立方根,数a的立方根记作读作“三次根号a”。
9.开立方的定义:求一个数的立方根的运算,叫做开立方。开立方和立方互为逆算。
10.立方根的性质:正数有一个正的立方根,负数有一个负的立方根,0的立方根0。
二、课堂小练习
1.的平方根________,的立方根_______。
2.若一正数的平方根是2a-1与-a+2,则。
3.如图,64、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是 __
4.直角三角形两条直角边的长分别为5、12,则斜边上的高为 .
5.已知甲往正东走了4km,乙往正南走了3km,这时甲、乙两人相距 .
6.一个长方形的长为12cm,对角线长为13cm,则该长方形的周长为 .
7.以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= .
8.在Rt△ABC中,∠C=90°若a=5,b=12,则c=________。
9.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是 ( )A.a+b=c B. a:b:c=3:4:5 C.a=b=2c D.∠A=∠B=∠C
10.若三角形三边长分别是6,8,10,则它最长边上的高为( )
A.6 B.4.8 C.2.4 D. 8
11.分别以下列四组数为一个三角形的边长:①6、8、10;②5、12、13;③8、5、17
④4、5、6.其中能构成直角三角形的有( )
A.4组 B. 3组 C. 2组 D.1组
12在ΔABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法中正确的个数有( )
①如果∠B-∠C=∠A,则ΔABC是直角三角形②如果c2=b2-a2,则ΔABC是直角三角形,且∠C=900③如果(c+a)(c-a)=b2,则ΔABC是直角三角形④如果∠A:∠B:∠C =5:2:3,则
ΔABC是直角三角形
A. 1 B. 2 C. 3 D. 4
三、例题讲解
例1:(1)x2-25=0 ; (2)4(x+1)2=81 ; (3)8x3+1=0。
例2:如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D,
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
例3:如图,在四边形ABCD中,∠BAD=900,∠DBC=900,AD=3,AB=4,BC=12,
求CD。
例4:如图,已知AD是BC边上的中线,如果BC=10㎝,AC=4㎝,AD=3㎝,求△ABC的面积。
四、检测反馈
1.把下列各数填入相应的集合内:-7,0.32,,0,,,- .
有理数集合:{ …}; 无理数集合:{ …};
2.请写出3个负的无理数:_________;请任意写出一组勾股数:________.
3在棱长为5的正方体木箱中,想放入一根细长的直钢管,则这根钢管的最大长度可以是________.
4.给出下列运算:①,② =±4,③ =-2,④,⑤= .其中,错误的有( ).
(A)2个 (B)3个 (C)4个 (D)5个
5.算术平方根等于它本身的数有________,立方根等于本身的数有________.
6.若,则________,若,则________.
7.已知两边为3,4,则第三边长________.
8.如果+(y+6)2=0,则________.
9.如果和是一个数的平方根,则
10.下面条件中,能判定四边形ABCD是平行四边形的有( )
(1)∠A=∠B,∠C=∠D;(2)AB∥CD ,AB=CD;(3)AB∥CD ,AD=BC ;(4)AB=CD,AD=CB;(5)AB∥CD ,∠A=∠C。
A. 1 B. 2 C. 3 D. 4
11.已知如图所示,四边形ABCD 求四边形ABCD的面积.
12.在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积。利用你的表示方法,你能得到勾股定理吗?
13.已知:与互为相反数,求(2x-y)2 的平方根。
14.如图,某菜农要修建一个育苗棚,棚宽a=12m,高b=5m,长d=20m,请你帮他算一下覆盖在顶上的塑料薄膜需多少?
15.如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积。
16.如图,A,B是直线l外同侧的两点,且点A和点B到l的距离分别是3㎝和5㎝,AB=12㎝,若点P在l上移动,
求PA+PB的最小值。
【布置作业】
《补充习题》同步练习
① ② ③ ④ ⑤
第1题
400
64
A
400
图4
图3
…
…
A
C
B
1
C
A
0
B
0
B
A
C
A
B
C
D
F
E
A
D
B
C
E
A
D
O
B
C
64
A
·B
·A
l
x
x
1
1
1
x
PAGE
32
主备人:顾风金 审核人:朱刚
2.1勾股定理(1)
班级 姓名
【学习目标】
1. 能说出勾股定理,并能应用勾股定理解决简单的问题。
2. 探索勾股定理的过程,发展合情推理的能力,体会数型结合的思想。
【学习重、难点】勾股定理的内容。应用勾股定理解决简单的问题。
一、课前导学
1. 直角三角形边、角有哪些性质?
2. 求下列图中表示边的未知数x、y、z的值. (课本45页练习第2题)
3. 湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=13千米,CB=12千米,则AB为 ( )
A.5千米 B.12千米 C.10千米 D.13千米
二、合作探究
活动一:观察分析这枚邮票的图案,你有哪些发现?
活动二:探究实验
1、小方格的面积看作1,以BC为一边的正方形的面积是16,以AC为一边的正方形的面积是9,你能计算出以AB为一边的正方形的面积吗?"
2、实验:在下面的方格纸上,任意画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,然后算出以斜边为一边的正方形的面积。你又发现了什么?
3、通过以上练习,你对直角三角形的三边之间的数量关系有什么联想?
勾股定理:
用字母表示:
活动三:验证勾股定理
三、典例精析
1、求下列直角三角形中未知边的长:
2、如图,将长为10米的梯子AC斜靠在墙上,BC长为6米
(1) 求梯子上端A到墙的底端B的距离AB.
(2) 若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?
3、如图,在△ABC中。∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB与D,求:(1),AC的长; (2)⊿ABC的面积; (3)CD的长。
四、盘点收获
本节课你有哪些收获?
五、检测反馈
1.A、B、C是△ABC的三边,
①A=5,B=12,C=13 ②A=8,B=15,C=17 ③A∶B∶C=3∶4∶5 ④A=15,B=20,C=25上述四个三角形中直角三角形有 ( )
A、1个 B、2个 C、3个 D、4个
2.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A、13 B、5 C、13或5 D、无法确定
3.将一个直角三角形两直角边同时扩大到原来的两倍,则斜边扩大到原来的 ( )
A、4倍 B、2倍 C、不变 D、无法确定
4.若直角三角形两直角边分别为6和8,则斜边为 ___________;
5.在Rt△ABC中,∠C=90°,BC∶AC=3∶4,AB=10,则AC=_______,BC=________
6.公路旁有一棵大树高为5.4米,在刮风时被吹断,断裂处距地面1.5米,请你通过计算说明在距离该大树多大范围内将受到影响。
7.如图,∠C=90°,AC=3,BC=4,AD=12,BD=13,试判断△ABD的形状,并说明理由。
8.已知直角三角形的三边分别是n-2,n,n+2,求n的值
9.如图,一个圆柱形纸筒的底面周长是40Cm,高是30Cm,一只小蚂蚁在圆筒底的A处,它想吃到上底与下底面中间与A点相对的B点处的蜜糖,试问蚂蚁爬行的最短的路程是
六、布置作业
《补充习题》同步练习
2.1勾股定理(2)
班级 姓名
【学习目标】
1.通过拼图,用面积的方法说明勾股定理的正确性.
2.通过实例应用勾股定理,培养学生的知识应用技能.
【学习重、难点】
1. 用面积的方法说明勾股定理的正确.
2. 勾股定理的应用.
一、课前导学
1、阅读课本第46页到第47页,完成下列问题:
(1)我国古代把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦。图(1)称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。图(2)是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就. 你能用不同方法表示大正方形的面积吗
2、剪四个完全相同的直角三角形,然后将它们拼成如图所示的图形。大正方形的面积可以表示为_______,又可以表示为____________.对比两种表示方法,看看能不能得到勾股定理的结论。用上面得到的完全相同的四个直角三角形,还可以拼成如下图所示的图形,与上面的方法类似,也能说明勾股定理是正确的(请逐一说明)。
归纳其共有的证明思路:利用图形的割补,借助前后的面积相等形成关于三边的数量关系。
二、合作探究:
(一)思索、交流:
拼图填空:剪裁出若干个大小、形状完全相同的直角三角形,三边长分别记为a、b、c,如图①.(1)拼图一:分别用4张直角三角形纸片,拼成如图②③的形状,观察图②③可发现,图②中两个小正方形的面积之和__________ (填“大于”、“小于”或“等于”)图③中小正方形的面积,用关系式表示为________ .(2)拼图二:用4张直角三角形纸片拼成如图④的形状,观察图形可以发现,图中共有__________个正方形,它们的面积之间的关系是________ ,用关系式表示为_____ .(3)拼图三:用8个直角三角形纸片拼成如图⑤的形状,图中3个正方形的面积之间的关系是_____ _____ ,用关系式表示________ _______ .
(二)应用、探究:
1、如图 ,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
2.如图,A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1km,BD=3km,CD=3km,现在河边CD上建一水厂向A、B两村输送自来水,铺设水管的费用为20000元/千米,请你在CD选择水厂位置O,使铺设水管的费用最省,并求出铺设水管的总费用F。
三、展示交流
1、如图,64、400分别为所在正方形的面积,则图中字
母A所代表的正方形面积是 _________ 。
2、直角三角形两条直角边的长分别为5、12,则斜边上的高为 。
3、已知甲往东走了4km,乙往南走了3km,这时甲、乙两人相距 。
4、一个长方形的长为12cm,对角线长为13cm,则该长方形的周长为 。
5、以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= 。
6、假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走了3千米,再折向北走了6千米处往东一拐,仅走了1千米就找到宝藏,问登陆点A到宝藏埋藏点B的距离是多少千米?
四、盘点收获
本节课我们进一步认识了勾股定理,并用两种方法证明了这个定理,在应用此定理解决问题时,应注意只有直角三角形的三边才有这样的关系,如果不是直角三角形应该构造直角三角形来解决。
五、检测反馈
1、填空
在RtΔABC中,∠C=900.
①若a=6,c=10 ,则b=____.
②若a:b=3:4,c=10,则a=____,b=____.
③若a=6,b=8,则斜边c上的高h=______.
2、选择:
①若直角三角形的三边为6、8、x,则x的长为 ( )
A.6 B.8 C.10 D.以上答案均不对
②如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,则这个距离为 ( )
A.1 B.3 C.4 D.5
③如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为 ( )
A.3 B.4 C.5 D.6
3、①如图3,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是7cm,则正方形A、B、C、D的面积之和是______。
②如图4,小方格的面积为1,找出图中以格点为端点且长度为5的线段。
3解答题
1、如图 ,以ΔABC的三边为直径的3个半圆的面积有什么关系 请你说明理由。
2、如图,正方形ABCD的边长为6,F是DC边上的一点,且DF∶FC=1∶2,E为BC的中点,连结AE、AF、EF。
(1)求△AEF的周长;(2)求△AEF的面积
3、 P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
六、布置作业
《补充习题》同步练习
2.2神秘的数组
班级 姓名
【学习目标】
1.会阐述直角三角形的判定条件(勾股定理的逆定理)
2.会应用直角三角形的判定条件判定一个三角形是直角三角形
3.经历探索一个三角形是直角三角形的条件的过程,发展合情推理能力,体会“形”与“数”的内在联系。
【学习重、难 点】1利用“三角形的三边a、b、c满足a2+b2=c2,那么这个三角形是直角三角形“这一条件进行直角三角形的判定
2了解勾股数的由来,并能用直角三角形的判定条件解决一些简单的实际问题
一、课前导学
阅读课本第48页到49页,完成下列问题:
1.请画一个三边分别为3cm,4cm,5cm的三角形,你有什么发现?
2.古巴比伦泥板上的数组揭示了什么奥秘?
3.请你画出两个三角形三边的长分别为6cm,8cm,10cm和5cm,12cm,13cm.你发现它们有什么共同的特点吗?
猜想:三角形的三边满足什么条件时,这个三角形是直角三角形?
二.合作探究
活动一:情境创设
1.古巴比伦泥板:美国哥伦比亚大学图书馆收藏着一块编号为“普林顿“322” (plinmpton322)的古巴比伦泥板,上面密密麻麻的写着什么呢? 泥板上的一些神秘符号实际上是一些数组,你知道这些数组揭示什么奥秘吗?
2.我们学过的直角三角形的判定方法有哪些?
活动二:合作交流
1、请你以3cm、4cm、5cm为三条边画三角形,再用量角器量出这个三角形各角的度数,与你的小组同学交流一下,你发现了什么?再以6cm、8cm、10cm呢?这些三角形的三边之间有什么关系?请把你的发现用自己的语言表达出来。
猜想:三角形的三边之间满足怎样数量关系时,此三角形是直角三角形?
如果三角形的三边长a、b、c满足 ,那么这个三角形是 .
用符号表示∵ ∴
这个结论与勾股定理有什么关系?
我们还把满足a2+b2=c2的三个正整数a,b,c称为勾股数,例如,3,4,5;6,8,10; 5,12,13这3组都是勾股数
2.你能猜想这些神秘的数组揭示什么奥秘了吗?请你验证你的猜想。
三、典例精析
例1 下列各组数是勾股数吗 为什么
(1) 12,15,18; (2)7,24,25 ;
(3) 15,36,39; (4)12,35,36.
例2: 3,4,5 是一组勾股数,如果将这三个数分别扩大2倍,所得的3个数还是勾股数吗 扩大3倍,4倍,n倍呢 为什么
例3:一个零件的形状如图,按规定这个零件中∠A 与∠DBC都应为直角,工人师傅量得零件各边尺寸:AD = 4,AB = 3, DC = 13 , BC=12,你能根据所给的数据说明这个零件是否符合要求吗?
四、盘点收获
1、这节课你学到了什么?
2、在学习过程中你还存在哪些问题?
五、检测反馈
1.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是 ( )
A. a+b=c B. a:b:c=3:4:5 C. a=b=2c D. ∠A=∠B=∠C
2.若三角形三边长分别是6,8,10,则它最长边上的高为 ( )
A. 6 B. 4.8 C. 2.4 D. 8
3.把三边分别BC=3,AC=4,AB=5的三角形沿最长边AB翻折成△ABC ,则CC 的长为 ( )
A. B. C. D.
4.在△ABC中,AB=13,AC=15,高AD=12,则BC的长为 ( )
A. 14 B. 4 C.14或4 D.以上都不对
5、下列各数组中,不能作为直角三角形的三边长的是( )
A、3,4,5 B、10,6,8 C、4,5,6 D、12,13,5
6、若△ABC的两边长为8和15,则能使△ABC为直角三角形的第三边的平方是( )
A、161 B、289 C、17 D、161或289
7、4个三角形的边长分别为:①a=5,b=12,c=13;②a=2,b=3,c=4; ③a=2.5,b=6,c=6.5; ④a=21,b=20,c=29.
其中,直角三角形的个数是( )
A、4 B、3 C、2 D、1
8. 在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=_______ .
9. 已知|x-12|+|x+y-25|与z2-10z+25互为相反数,则以x、y、z为三边的三角形是______ 三角形.
10 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,先将直角
边AC沿AD折叠,使它落在斜边AB上,且与AE重合,则CD= .
11.若△ABC的三边a、b、c满足条件a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
12.如图,在四边形ABCD中,已知:AB=1,BC=2,CD=2,AD=3,且AB⊥BC.试说明AC⊥CD的理由.
13. 已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,BC=12.求图形的面积.
14. 欲将一根长129cm的木棒放在长、高、宽分别是40cm、30cm、120cm的木箱中,能放得进去吗?请说明理由.
15、如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30cm,DC=12cm,AB=3cm,BC=4cm,求△ABC的面积。
16.要做一个如图所示的零件,按规定∠B与∠D都应为直角,工人师傅量得所做零件的尺寸如图,这个零件符合要求吗?
17.如图,已知AD是BC边上的中线,如果BC=10㎝,AC=4㎝,AD=3㎝,求△ABC的面积。
六、布置作业
《补充习题》同步练习
2.3 平方根(1)
班级 姓名
【学习目标】了解数的平方根的概念.会用根号表示一个数的平方根。
了解开平方与乘方是互逆的运算,会求非负数的平方根。
【学习重、难点】一个数的平方根的概念理解及表示方法
一、课前导学
1.一个数的平方等于它本身,这个数是 。一个数的平方根等于它本身,这个数是 。
2.若3a+1没有平方根,那么a一定 。
3.若4a+1的平方根是±5,则a= 。
4.一个数x的平方根等于m+1和m-3,则m= 。x= 。
5.若|a-9|+(b-4) =0,则 ab的平方根是 。
6. 求下列各式中的x:
(1) x =16 (2) x =9 (3) x =15 (4) 4x =81
二、合作探究
活动一:设图中小方格的边长为1,你能分别说出图中两个长方形的对角线AB、A′B ′的长吗?
活动二:交流 如果一个数的平方等于9,这个数是几? 一个数的平方等于2呢?
活动三:引出概念、掌握表示方法
例如:2 =4,(-2) =4,±2叫做4的平方根。
10 =100,(-10) =100,±10叫做100的平方根
13 =169,(--13) =169,±13叫做169的平方根。
一般地,如果一个数的平方等于a,那么这个数叫做a的 ,也称为 。
也就是说,如果 ,那么 叫做 的平方根。
表示方法:一个正数的平方根有 个,它们互为 。一个正数a的正的平方根,记作“ ” 一个正数a的负的平方根记作“- ”,这两个平方根合起来记作“± ”,读作“正负根号a”。
例如,2的平方根记作“± ”,读作“正负根号2”。81的平方根记作“± ”,读作“正负根号81”
活动四:尝试交流、引出结论
1.9的平方根是什么?25的平方根是什么?
2.0的平方根是什么?0的平方根有几个?
3.-4、-8、-36有平方根吗?为什么?
结论:
求一个数a的平方根的运算,叫做开平方.
三、典例精析
例: 求下列各数的平方根:
(1)25; (2)0.81; (3)15; (4)(-2)
四、展示交流
求下列各数的平方根:
81 289 0 2.56
五、盘点收获
本节课你有哪些收获?
六、检测反馈
1.下列说法正确的是( ).
A.的平方根是 B.2是4的平方根
C.任何数的平方是非负数,因而任何数的平方根也是非负数
D.任何一个非负数的平方根都不大于这个数
2.的平方根是( ).
A. B.12 C D.
3.下列各数没有平方根的是( ).
A.18 B. C. D.11.1
4.如果有意义,则x可以取的最小整数为( ).
A.0 B.1 C.2 D.3
5.的值是( ).
A. B.3 C. D.9
6.下列说法不正确的是( ).
A.表示两个数:或 B.的指数是2
C.在数轴上表示正数的两个平方根的两个点,总是关于原点对称
D.正数的两个平方根的积为负数
7.若,则x+y的值是( ).
A.-2 B.-3 C.-4 D.无法确定
8.一个数如果有两个平方根,那么这两个平方根的和是( ).
A.大于0 B..等于0 C.小于0 D.大于或等于0
9.若a≥0,则4a2的平方根是( ).
A.2a B.±2a C. D.∣2a∣
10.25的平方根记作 ,结果是 .
11.361的平方根是 ,
12.(-4)2的平方根是 。
13.-9是数a的一个平方根,那么数a的另一个平方根是 ,数a是 。
14.若,则y= .
15.求下列各式的值:
⑴= ⑵ = ⑶= .
⑷= ⑸= ⑹= .
16.求下列各式中的x.
⑴若x2=49,则x= . ⑵若4(x-1)2=25,则x= .
⑶若9(x2+1)=10,则x= . ⑷若=3,则x= .
17.已知与互为相反数,求(x-y)2的平方根。
18.已知2a-1的平方根是±3,3a+b-1的平方根为±4,求a+2b的平方根。
19.如果一个直角三角形的两边长分别是5㎝和12㎝,那么这个三角形的面积是多少?
20.某纸箱加工厂,有一批边长为40㎝的正方形硬纸板,现准备将此纸板折成没盖的纸盒。首先在四个角上截去四个相同的小正方形,然后做成底面积为625㎝2的纸盒子,想一想,你怎样求出截去的小正方形的边长?
七、布置作业
《补充习题》同步练习
2.3 平方根(2)
班级 姓名
【学习目标】了解数的算术平方根的概念.会用根号表示一个数的算术平方根。
能运用算术平方根解决实际问题。
【学习重、难点】根据一个数的算术平方根的意义解决有关问题。
一、课前导学
1.正数a有 个平方根,其中正数a的正的平方根,也叫做a的 。
例如:4的平方根是 ,其中 叫做4的算术平方根,记作 ,
2的平方根是 ,其中 叫做2的算术平方根,
0只有一个平方根,0的平方根也叫做0的算术平方根,即 =0
2.面积为15m2正方形的边长是多少?
二、交流合作
活动一:组内交流
1. 16的算术平方根的平方根是什么? 5的算术平方根是什么?
2、 0的算术平方根是什么?0的算术平方根有几个?
3、 -2、-5、-6有算术平方根吗?为什么?
活动二:讨论
1.等于多少?呢?
2. 等于多少?等于多少?等于多少
三、典例精析
例1:求下列各数的算术平方根:
(1)625; (2)0.81; (3)6; (4)(-2)
例2:“欲穷千里目,更上一层楼”。说的是登的高看得远。若观测点的高度为h,观测者视线能达到的最远距离为d≈ ,其中R是地球半径(通常取6400km),小丽站在海边一块岩石上,眼睛离地面的高度为20M,她观测到远处一艘船刚露出海平面,此时该小船离小丽有多远?
四、展示交流
1.一个数的算术平方根等于它本身,这个数是 。
2.若x =16,则5-x的算术平方根是 。
3.若4a+1的平方根是±5,则a 的算术平方根是 。
4.16的平方根等于 ,算术平方根等于 。
5.在△ABC中,∠C=90°.(1)如果AC=5,BC=12,求AB;(2)如果AC=2,BC=1,求AB;(3)如果AB=25,BC=24,求AC;(4)如果AC=5,AB=12,求BC;
五、盘点收获
平方根与算术平方根的区别与联系
六、检测反馈
1.下列语句正确的是( )
A.一个数的平方根一定是两个数 B.一个非负数的非负平方根一定是它的算术平方根
C.一个正数的平方根一定是它的算术平方根 D.一个非零的正的平方根是它的算术平方根
2.若有意义,则a能取的最小整数为( ).
A.0 B.1 C.-1 D.-4
3.若,则x+y的值是( ).
A.-2 B.-3 C.-4 D.无法确定
4.一个数的算术平方根只要存在,那么这个算术平方根( ).
A.只有一个,并且是正数 B.不可能等于零 C.一定小于这个数 D.必定是非负数
5.若a是有理数,下列说法正确的是( ).
A. a2的算术平方根是a B. a2的平方根是a
C. a2的算术平方根是∣a∣ D. a2的平方根是∣a∣
6.一个数如果有两个平方根,那么这两个平方根发和是( ).
A.大于0 B..等于0 C.小于0 D.大于或等于0
7.若a≥0,则4a2的算术平方根是( ).
A.2a B.±2a C. D.∣2a∣
8.的算术平方根是( ).
A.4 B.±4 C.2 D.±2
9.(-4)2的算术平方根是 36的倒数的算术平方根的相反数是________.
10.的最小值是________,此时a的取值是________.
11.的算术平方根是2,x=________.
12.已知正数a和b,有下列命题:(1)若,则≤(2)若,则≤
(3)若,则≤ 根据以上三个命题所提供的规律猜想:若,则≤________.
13.一个正数的两个平方根的和是________.
14.一个正数的两个平方根的商是________.
15.如果,那么x=________;如果,那么________.
16.当时,________.
17.一个数的平方根等于它本身,那么这个数是________.
18.计算:
19.求下列各式中x的值.
20.下列各式中,哪些有意义?
(1) (2) (3) (4) (5)
21.已知的平方根是,的平方根是,求的平方根.
22.如图所示,已知正方形ABCD的面积是49平方厘米,正方形EFGH的面积是25平方厘米,且AH=DG=CF=BE,BF=CG=DH=AE,求AD的长;EF的长;△AEH的面积.
七、布置作业
《补充习题》同步练习
2.4 立方根
班级 姓名
【学习目标】
1. 在一定的情境只,理解立方根的概念,使学生不断获得解决问题的经验,提高思维水平,学习中要注意感悟"类比"在知识产生和发展过程中的作用。
2. 了解立方根的概念,会用根号表示一个数的立方根,了解开立方与立方互为逆运算,能用立方运算求一些数的立方根
3. 能用立方根解决一些简单的实际问题。
【学习重、难点】正确地理解立方根的概念及符号表示并能熟练应用
一、课前导学
(1)1的立方根是________,-1的立方根是________,0的立方根是________.
(2)求下列各数的立方根:
(1)-; (2)-(-0.216); (3)10-3.
二、合作探究
活动一:解决以下问题
1. 现有一只体积为216cm3的正方体纸盒,它的每一条棱长是多少?
2.阅读课本第55页到56页。完成下列问题:
①观察思考:如图,棱长为1时,正方体的体积是13=1,设体积为2的正方体的棱长为x.依题意列方程得: .
②体积为1的正方体,棱长为多少?体积增加1,棱长为多少?
③做一个正方体纸盒,使它的容积为64cm,正方体纸盒的棱长是多少?如果要使正方体纸盒容积为25cm,它的棱长是多少?
活动二:归纳概念
定义:1、一般地,如果一个数的立方等于a,这个数就叫做a的 ,也称为 .也就是说,如果x3=a,那么x叫做a的 ,数的立方根记作 ,读作
例如:4的立方是 所以4是64的立方根,记作 ,又如,x是2的立方根,记作
2、求一个数的立方根的运算叫做
3、立方根的性质:正数有 立方根,负数有 立方根,0的立方根是
三、典例精析
1.求下列各数的立方根
⑴, ⑵ , ⑶0, ⑷
2.求下列各式的值⑴,⑵,⑶,⑷
3.求下列各式中的x
x+729=0 (x-3)=64
四、盘点收获
⑴掌握立方根的定义和性质;⑵会求一个数的立方根;⑶理解并掌握公式
五、检测反馈
1、立方根等于本身的数是 ( )
A、±1 B、1,0 C、±1,0 D、以上都不对
2、若一个数的算术平方根等于这个数的立方根,则这个数是( )
A、±1 B、±1,0 C、0 D、0,1
3、下列说法中,错误的是( )
A、64的立方根是4 B、立方根 C、的立方根是2 D、125的立方根是±5
4、下列说法正确的是( )
A、1的立方根与平方根都是1 B、C、的平方根是 D、
5.-6的立方根用符号表示,正确的是( )
A B - C - D
6.下列说法正确的是( )
A、任意数a的平方根有2个,它们互为相反数 B、任意数a的立方根有1个
C、-3是27的负的立方根 D、(-1)的立方根是-1
7.下列判断正确的是( )
A、64的立方根是4 B、(-1)的立方根是1C、的立方根是2 D、如果=a,则a=0
8.(-1)的立方根是 —0.0027的立方根是
9.已知x=64,则=
10.= , =
11. a为何值时,则 , a, , 中,必是非负数的有
12.求下列各数的立方根
⑴,⑵512,⑶—729,⑷
13.求下列各式中的
⑴, ⑵, ⑶
14 .已知一个正方体的棱长是5cm,再做一个正方体,使它的体积等于原正方体的体积的8倍,求要做的正方体的棱长。
六、布置作业
《补充习题》同步练习
2.5 实数(1)
班级 姓名
【学习目标】 1.知道无理数是客观存在的,了解无理数和实数的概念,能对实数按要求进行分类,同时会判断一个数是有理数还是无理数。
2.知道实数和数轴上的点一一对应。
3.经历用有理数估算的探索过程,从中感受“逼近”的数学思想,发展数感,激发学生的探索创新精神。
【学习重、难点】会判断一个数是有理数还是无理数。
一、课前导学
1.实数两种常见的分类形式:
2.把下列各数填入相应的集合之中:
0.456、-、(-)0、3.14、-0.801 08、0、0.101 001 000 1…(每两个1之间依次增加一个0)、、-1.
有理数集合 无理数集合
3.任意写出3个无理数:________________.
二、合作探究
活动一:创设情境
情境一:提出问题—我们通过研究边长为1的正方形的对角线的长为,说说你对的认识。
情境二:现有一个直角三角形,直角边均为1,斜边为多少?你认识这个数吗?
情境三:大家都知道2是一个有理数,它的算术平方根为多少?还是一个有理数吗?
情境四:为了生活的需要人们引入了负数,数就由原来的正数和0扩充为有理数。细心的同学会发现还有一些不是有理数的数,和有理数一起构成了实数,它们到底是什么数呢?
活动二:探索活动
问题1:是有理数吗?
问题2:是一个整数吗?
问题3:是1与2之间的一个分数吗?(也就是1与2之间的分数的平方会等于吗?)
问题4:有多大?
三、例题精析
例:把下列各数填入相应的集合内:
、、0、、、、3.14159、-0.020020002 0.12121121112…
(1)有理数集合{ }
(2)无理数集合{ }
(3)正实数集合{ }
(4)负实数集合{ }
四、展示交流
1.判断正误,若不对,请说明理由,并加以改正。
(1)无理数都是无限小数。 (2)带根号的数不一定是无理数。
(3)无限小数都是无理数。 (4)数轴上的点表示有理数。
(5)不带根号的数一定是有理数。
2. .数、、中,无理数有( ).
(A)0个 (B)1个 (C)2个 (D)3个
3.(1)把下列各数填入相应的集合内:-7,0.32,, ,,- .
有理数集合:{ …};无理数集合:{ …};
无理数集合:{ …}.
五、盘点收获
本节课你有哪些收获?
六、检测反馈
⒈ 在5,0.1,-π,,,,,八个实数中,无理数的个数是 ( )
A.5 B.4 C.3 D.2
⒉ 下列说法中正确的是 ( )
A.有理数和数轴上的点一一对应 B.不带根号的数是有理数
C.无理数就是开方开不尽的数 D.实数与数轴上的点一一对应
⒊ 无理数有 ( )
A.最小的数 B.最大的数 C.绝对值最小的数 D.以上都不对
⒋ 在实数,,3.14,π,,中属于有理数集合的数有 ;属于负实数集合的数有 ;属于无理数集合的数有 .
⒌ 的相反数是 ;倒数是 .
⒍ 点M在数轴上与原点相距个单位,则点M表示的实数为 ,数轴上到的点距离为的点所表示的数是 .
⒎ 已知x,y都是实数,且y=,试求xy的值.
⒏ 若a,b为有理数,且有a,b满足a2+2b+b=17-,求a+b的值.
⒐ 设m是的整数部分,n是的小数部分,试求m-n的值.
⒑ 实数a,b互为相反数,c,d互为倒数,x的绝对值为.
求代数式x2+(a+b+cd)x++的值.
⒒ 如图,在长方形ABCD中,∠DAE=∠CBE=45°,AD=1,求△ABE的面积和周长.
七、布置作业
《补充习题》同步练习
2.5 实数(2)
班级 姓名
【学习目标】
1、了解实数的意义,能对实数按要求进行分类。
2、了解实数范围内,相反数、倒数、绝对值的意义。
3、了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数。
【学习重点、难点】了解实数意义,能对实数进行分类,明确数轴上的点与实数一一对应并能用数轴上的点来表示无理数。
一、课前导学
1、判断下列说法是否正确:(1)无限小数都是无理数;(2)无理数都是无限小数; (3)带根号的数都是无理数。
2、求下列各数的相反数、倒数和绝对值:
(1)3.8 (2) (3) (4) (5)
3、在数轴上作出对应的点。
4.实数可分为 与 。
二、合作交流
活动一:在实数概念基础上对实数进行不同分类。
无理数与有理数一样,也有正负之分,如是正的,是负的。
思考:
(1)你能把,,,,,,,,,,0,0.3737737773……(相邻两个3之间7的个数逐次增加1)等各数填入下面相应的集合中?
正有理数:
负有理数:
有理数:
无理数:
(2)0属于正数吗?0属于负数吗?
(3)实数除了可以分为有理数与无理数外,实数还可怎样分?
活动二:了解实数范围内相反数、倒数、绝对值的意义:
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
例如,和是互为相反数,和互为倒数。
,,,。
活动三:想一想
1、a是一个实数,它的相反数为 ,绝对值为 ;
2、如果,那么它的倒数为 。
活动四:议一议。
探索用数轴上的点来表示无理数
1.复习勾股定理。如图在Rt△ABC中AB= a,BC = b,AC = c,其中a、b、c满足什么条件。
当a=1,b=1时,c的值是多少?
2.让学生探讨以下问题:
(A)如图OA=OB,数轴上A点对应的数是多少?
(B)如果将所有有理数都标到数轴上,那么数轴上被填满了吗?
三、盘点收获
本节课你有哪些收获?
四、检测反馈
⒈已知0<x<1,那么在x,,,x2中最大的是( )
A.x B. C. D.x2
⒉若实数a,b满足a+b>0,a b<0,则下列不等式中正确的是 ( )
A.|a|>|b| B.当a>0,b<0时,|a|>|b|
C.|a|<|b| D.当a<0,b>0时,|a|>|b|
⒊如图,数轴上表示1,的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为 ( )
A.-1 B.1- C.2- D.-2
⒋ 如果一个实数的绝对值是,那么这个实数是 .
⒌ 若a,b都是无理数,且a+b=2,则a,b的值可以是 (填上一组满足条件的值即可).
⒍ 若|x-|+(y+)2=0,则(x·y)2005= .
⒎ 比较下列各组数的大小:
⑴与 ⑵与 ⑶与
⒏ 计算:
⑴;(保留两位小数)
⑵.(保留两位小数)
⒐ 求下列各式中x的值:
⑴ ; ⑵ .
⒑ 如图,a,b,c是数轴上三个点A、B、C所对应的实数.
试化简:.
11已知实数x满足|x-3|+|x+3|=-2x,试求x的取值范围.
五、布置作业
《补充习题》同步练习
2.6近似数与有效数字
班级 姓名
【学习目标】
1.了解近似数与有效数字的概念,体会近似数的意义及在生活中的作用
2.能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数
【学习重、难点】按要求用四舍五入法取一个数的近似数
一、课前导学
自学教材P62-63页的内容
二、合作交流
活动一:情境创设
李宇春以3528308条短信获得冠军 周笔畅以3270840条短信获得亚军
张靓颖则以1353906条短信获得季军
今年22岁的夏洛特·凯利4年前生出詹尼弗和简孪生姐妹,今年7月30日又生出鲁思和艾米丽两位可爱的孪生小姐妹。艾米丽出生时体重约为8.12磅,鲁思出生时的体重则为约7.20磅。
活动二:认识近似数
实际生产生活中的许多数据都是近似数,例如测量长度,时间,速度所得的结果都是近似数,且由于测量工具不同,其测量的精确程度也不同。在实际计算中对于像π这样的数,也常常需取它们的近似值.请说说生活中应用近似数的例子。
取一个数的近似值有多种方法,四舍五入是最常用的一种方法。用四舍五入法取一个数的近似数时,四舍五入到哪一位,就说这个近似数精确到哪一位.
例如,圆周率=3.1415926…
取π≈3,就是精确到个位(或精确到1)取π≈3.1,就是精确到十分位(或精确到0.1)
取π≈3.14,就是精确到百分位位(或精确到0.01)
取π≈3.142,就是精确到千分位位(或精确到0.001)
活动三:认识有效数字
对一个近似数,从左面第一个不是0的数字起,到末位数字止,所有的数字都称为这个近似数的有效数字。
例如:上面圆周率π的近似值中,3.14有3个有效数字3,1,4;3.142有4个有效数字3,1,4,2.
三、典例精析
例1 小亮用天平称得罐头的质量为2.026kg,,按要求取近似数,并指出每个近似数的有效数字:
(1)精确到0.01kg; (2)精确到0.1kg; (3)精确到1kg.
例2 用四舍五入法,按要求对下列各数取近似值,并用科学记数法表示.
(1) 地球上七大洲的面积约为149480000(保留2个有效数字)
(2) 某人一天饮水1890ml(精确到1000ml)
(3) 小明身高1.595m(保留3个有效数字)
(4) 人的眼睛可以看见的红光的波长为0.000077cm(精确到0.00001)
四、展示交流
1. 教材P63第 1、2题
2 .创新探究
张娟和李敏在讨论问题。
张娟:如果你把7498近似到千位数,你就会得到7000.
李敏:不,我有另外一种解答方法,可以得到不同的答案。首先将7498近似到百位得7500,接着把7500近似到千位,就得到8000。
张娟:……
你怎样评价张娟和李敏的说法呢?
3. 研究性学习练习
有一个四位数x,先将它四舍五入到十位,得到近似数m,再把四位数m四舍五入到百位,得到近似数n,再把四位数n四舍五入到千位,恰好是2000,你能求出四位数x的最大值与最小值吗?
五、盘点收获
本节课你有哪些收获?
六、检测反馈
⒈ 圆周率π=3.1415926…精确到千分位的近似数是 ( )
A.3.14 B.3.141 C.3.142 D.3.1416
⒉ 近似数3.14×104的有效数字有 ( )
A.1个 B.2个 C.3个 D.4个
⒊ 2004年某市完成国内生产总值(GDP)达3466.53亿元,用四舍五入法取近似值,保留3个有效数字,并用科学记数法表示,其结果是 ( )
A.3.47×103亿元 B.3.47×104亿元
C.3.467×103亿元 D.3.467×104亿元
⒋ 对于近似数10.08与0.1008,下列说法正确的是 ( )
A.它们的有效数字与精确位数都不相同 B.它们的有效数字与精确位数相同
C.它们的精确位数不同,有效数字相同 D.它们的有效数字不同,精确位数相同
⒌ 近似数1.69万精确到 位,有 个有效数字,有效数字是 .
⒍ 小明的体重约为51.51千克,如果精确到10千克,其结果为 千克;如果精确到1千克,其结果为 千克;如果精确到0.1千克,其结果为 千克.
⒎ 2003年10月15日9时10分,我国神舟五号载人飞船准确进入预定轨道.16日5时59分,返回舱与推进舱分离,返回地面.其间飞船绕地球共飞行了14圈,飞行的路程约为60万km,则神舟五号载人飞船绕地球平均每圈飞行 km(用科学记数法表示,结果保留3个有效数字).
⒏ 计算:⑴3+-(保留两个有效数字) ⑵(精确到0.01)
⒐ 以下问题中的近似数各精确到哪一位?各有几个有效数字?
⑴我国人口约为13亿人;
⑵π的近似值是3.14;
⑶某厂2004年的产值约为2000万元,约是1998年的6.8倍.
⒑ 用四舍五入法,,按要求对下列各数取近似值,并用科学记数法表示:
⑴太空探测器“先驱者10号”从发射到2003年2月人们收到它最后一次发回的信号时,它已飞离地球12200000000km(保留2个有效数字);
⑵2005年6月5日是世界第34个世界环境日,目前全球海洋总面积约为36105.9万km2(保留3个有效数字);
⑶光年是天文学中的距离单位,1光年大约是9500000000000km;
⑷某市全年的路灯照明用电约需4200万kw·h(精确到百万位).
六、布置作业
《补充习题》同步练习
2.7勾股定理的应用(1)
班级 姓名
【学习目标】
1、能运用勾股定理及直角三角形的判定条件解决实际问题.
2、在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.
【学习重、难点】勾股定理的实际运用;转化思想的过程渗透。
活动一:情境创设 、复习回忆
提出问题:如果知道桥面以上的索塔AB的高,怎样计算拉索AC、AD、AE、AF、AG的长?
直角三角形两直角边的平方和等于斜边的平方
a2+b2=c2 AC2+BC2=AB2
活动二:例题教学
例1 南京玄武湖东西隧道与中央路北段及龙蟠路大致成直角三角形,从C处到B处,如果直接走湖底隧道CB,比绕道CA (约1.36km)和AB (约2.95km)减少多少行程 (精确到0.1km)
活动三:探索活动
一架长为10m的梯子AB斜靠在墙上.
⑴ 若梯子的顶端距地面的垂直距离为8m,则梯子的顶端A与它的底端B哪个距墙角C远
⑵在⑴中如果梯子的顶端下滑1m,那么它的底端是否也滑动1m
⑶有人说,在滑动过程中,梯子的底端滑动的距离总比顶端下滑的距离大,你赞同吗
活动四:展示交流
1.如图,太阳能热水器的支架AB长为90cm,与AB垂直的BC长120cm.太阳能真空管AC有多长
2. 如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 ( )
A.7m B.8m C.9m D.10m
3. 一种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
活动五:盘点收获
我们知道勾股定理揭示了直角三角形的三边之间的数量关系,已知直角三角形中的任意两边就可以依据勾股定理求出第三边.从应用勾股定理解决实际问题中,我们进一步认识到把直角三角形中三边关系“a2+b2=c2”看成一个方程,只要依据问题的条件把它转化为我们会解的方程,就把解实际问题转化为解方程.
活动六:检测反馈
1.分别以下列四组为一个三角形的三边的长:①6、8、10;②5、12、13;③8、15、17;④7、8、9,其中能构成直角三角形的有( ).
A.4组 B.3组 C.2组 D.1组
2.等腰三角形底边上高是8,周长为32,则这个等腰三角形的面积为( ).
A.56 B.48 C.40 D.30
3.要从电杆离地面5m处向地面拉一条长为13m的电缆,则地面电缆固定点与电线杆底部的距离应为( ).
A.10m B.11m C.12m D.13m
4.一海轮以24n mile/h的速度从港口A出发向东南方向航行,另一海轮以18n mile/h的速度同时从港口A出发向西南方向航行,离开港口2h后,两海轮之间的距离为( ).
A. 84n mile B. 60n mile C. 48n mile D.36 n mile
5.如图,已知S1、 S2和 S3分别是 RtΔABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S1、 S2和 S3满足关系式为( ).
A. S1< S2 +S3 B. S1= S2+ S3 C. S1> S2+ S3 D. S1= S2 S3
6.现有两根木棒,长度分别为44㎝和55㎝.若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是( ).
A.22㎝ B.33㎝ C.44㎝ D.55㎝
7.如图,在高为5m,坡面长为13m的楼梯表面铺地毯,地毯的长度至少需要 ( ).
A.17m B.18m C.25m D.26m
8.等腰三角形ABC的面积为12㎝2,底上的高AD=3㎝,则它的周长为 。
9.轮船在大海中航行,它从A点出发,向正北方向航行20㎞,遇到冰山后,又折向东航行15㎞,则此时轮船与A点的距离为 ㎞。
10.如图,为测湖两岸A、B间的距离,小兰在C点设桩,使△ABC为直角三角形,并测得BC=12m,AC=15m,则A、B两点间的距离是 m。
11.如果梯子的底端离建筑物7m,则25m的消防梯可到达建筑物的高度是 m。
12. 甲、乙两人同时从同一地点出发,甲往东走了4km,乙往南走了6km,这时甲、乙两人相距__________km.
13.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(取3)是( ).
(A)20cm (B)10cm (C)14cm (D)无法确定
14.如图,铁路上A、B两点相距25㎞,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15㎞,CB=10㎞,现在要在铁路AB上修建一个土特产收购站E,使得C、D两村到E站的距离相等,则E站应修建在离A站多少千米处?
15.如图,在四边形ABCD中,AC⊥DC, △ADC的面积为30,DC=12,AB=3,BC=4,求△ABC的面积
【布置作业】
《补充习题》同步练习
2.7勾股定理的应用(2)
班级 姓名
【学习目标】能运用勾股定理及直角三角形的判定条件解决实际问题、构造直角三角形及正确解出此类方程
【学习难点】在运用勾股定理解决实际问题的过程中,感受数学的“转化”思想(把解斜三角形问题转化为解直角三角形的问题),进一步发展有条理思考和有条理表达的能力,体会数学的应用价值.要善于运用直角三角形三边关系,关键是根据实际情形准确构造出直角三角形。
【学习过程】
活动一:情境创设
这些图形有什么共同特征
活动二:探索活动
问题一 在右图的直角三角形中,利用勾股定理可知 x=,根据已有的知识,你还知道哪些与这个三角形有关的数据信息吗
问题二 你知道与下图的三角形有关的哪些数据信息呢
问题三 如果要知道一个等边三角形的有关信息,你认为至少需要哪些信息 与同学交.
3.例题教学
图1中的x等于多少 图2中的x、y、z等于多少 沿着图2继续画直角三角形,还能得到那些无理数
1)利用图2你们能在数轴上画出表示的点吗 请动手试一试!
2)怎样在数轴上画出表示 的点呢
3)在数轴上表示的点怎样画出
例1 如图,等边三角形ABC的边长是6,求△ABC的面积。
1、如图5,在△ABC中,AB=AC=17,BC=16,求△ABC的面积
2、如图6,在△ABC中,AD⊥BC,AB=15,AD=12,AC=13,求△ABC的周长和面积。
例2 交流材料
材料1:如图7,在△ABC中,AB=25,BC=7,AC=24,问△ABC是什么三角形?
材料2:如图8,在△ABC中,AB=26,BC=20,BC边上的中线AD=24,求AC.
材料3: 如图9,在△ABC中, AB=15,AD=12,BD=9,AC=13,求△ABC的周长和面积。
议一议:勾股定理与它的逆定理在应用上有什么区别?
试一试:如图,以△ABC的三边为直径向外作半圆,且S1+S3=S2,试判断△ABC的形状?
活动三:盘点收获
从勾股定理的应用中我们进一步体会到直角三角形与等腰三角形有着密切的联系;把研究等腰三角形转化为研究直角三角形,这是研究问题的一种策略.
活动四:检测反馈
1.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2=________.
2.如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是__________.
3. 在Rt△ABC中,∠ACB=90°,AC=4,BC=3.求Rt△ABC斜边上的高.
4. 已知一个三角形的三边长分别是12cm、16cm、20cm,你能计算出这个三角形的面积吗?
5. 邮递员从车站O正东1km的邮局A出发,先向正北走了3km到B,又向正西走了4km到C,最后再向正南走了6km到D,那么最终该邮递员与邮局的距离为多少km?
6.如图,已知,EB⊥AD于C,EB=FC,AB=CD,说明AF=ED。
7.如图,已知点B、E、C在一条直线上,∠B=∠C=90°,AE=ED,AB=EC,说明△AED是等腰直角三角形。
8.如图,已知∠B=∠C,∠A=90°,AC=BD,说明AB=CD。
9.如图,已知:等腰直角△ABC中,P为斜边BC上的任一点.
求证:PB2+PC2=2PA2 .
10.如图,在的正方形网格中,每个小正方形的边长都为1.请在所给网格中按下列要求画出图形.
1 点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为 ;
2 以⑴中的AB为边的一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数.
【布置作业】
《补充习题》同步练习
2.8小结与思考
班级 姓名
【学习目标】1回顾勾股定理及其逆定理,利用勾股定理解决生活中的实际问题
2平方根及立方根,能说出一个近似数的精确度或有几个有效数字,能按照要求用四舍五入的方法取一个数的近似数,会进行实数的有关计算
【学习难点】勾股定理及其应用,平方根及立方根
【教学过程】
一、知识要点
1.勾股定理:在一个直角三角形中,两直角边的平方和等于斜边的平方。
2.勾股定理的应用:在一个直角三角形中,知道其中的任意两边都可以求第三边。
①c2=a2+b2;②a2=c2-b2;③b2=c2-a2。
3.直角三角形的识别(勾股定理的逆定理):如果三角形的三边长a、b、c满足a2+b2 =c2,那么这个三角形是直角三角形。(这是判定一个三角形是直角三角形的又一种方法)
4.平方根的定义:一般地,如果一个数的平方等于a,那么这个数叫做a的平方根。也称二次方根,也就是说,如果x2=a,那么x就叫做a的平方根。
5.平方根的性质:①一个正数有两个平方根,它们互为相反数;②0的平方根是0,记作;③负数没有平方根。
6.开平方的定义:求一个数a的平方根的运算,叫做开平方。
7.算术平方根的定义:正数a有2个平方根,其中正数a的正的平方根,也叫做a的算术平方根。公式:()2=a (a≥0),=a (a≥0) , =-a(a≤0)。
8.立方根的定义:一般地,如果一个数的立方等于a,这个数就叫做a的立方根,也称为三次方根;也就是说,如果x3=a,那么x叫做a的立方根,数a的立方根记作读作“三次根号a”。
9.开立方的定义:求一个数的立方根的运算,叫做开立方。开立方和立方互为逆算。
10.立方根的性质:正数有一个正的立方根,负数有一个负的立方根,0的立方根0。
二、课堂小练习
1.的平方根________,的立方根_______。
2.若一正数的平方根是2a-1与-a+2,则。
3.如图,64、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是 __
4.直角三角形两条直角边的长分别为5、12,则斜边上的高为 .
5.已知甲往正东走了4km,乙往正南走了3km,这时甲、乙两人相距 .
6.一个长方形的长为12cm,对角线长为13cm,则该长方形的周长为 .
7.以直角三角形的三边为边向形外作正方形P、Q、K,若SP=4,SQ=9,则Sk= .
8.在Rt△ABC中,∠C=90°若a=5,b=12,则c=________。
9.在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,下列条件中,能判断△ABC为直角三角形的是 ( )A.a+b=c B. a:b:c=3:4:5 C.a=b=2c D.∠A=∠B=∠C
10.若三角形三边长分别是6,8,10,则它最长边上的高为( )
A.6 B.4.8 C.2.4 D. 8
11.分别以下列四组数为一个三角形的边长:①6、8、10;②5、12、13;③8、5、17
④4、5、6.其中能构成直角三角形的有( )
A.4组 B. 3组 C. 2组 D.1组
12在ΔABC中,∠A、∠B、∠C的对边分别是a、b、c,下列说法中正确的个数有( )
①如果∠B-∠C=∠A,则ΔABC是直角三角形②如果c2=b2-a2,则ΔABC是直角三角形,且∠C=900③如果(c+a)(c-a)=b2,则ΔABC是直角三角形④如果∠A:∠B:∠C =5:2:3,则
ΔABC是直角三角形
A. 1 B. 2 C. 3 D. 4
三、例题讲解
例1:(1)x2-25=0 ; (2)4(x+1)2=81 ; (3)8x3+1=0。
例2:如图,在⊿ABC中,∠ACB=900,AB=5cm,BC=3cm,CD⊥AB与D,
求:(1)AC的长; (2)⊿ABC的面积; (3)CD的长。
例3:如图,在四边形ABCD中,∠BAD=900,∠DBC=900,AD=3,AB=4,BC=12,
求CD。
例4:如图,已知AD是BC边上的中线,如果BC=10㎝,AC=4㎝,AD=3㎝,求△ABC的面积。
四、检测反馈
1.把下列各数填入相应的集合内:-7,0.32,,0,,,- .
有理数集合:{ …}; 无理数集合:{ …};
2.请写出3个负的无理数:_________;请任意写出一组勾股数:________.
3在棱长为5的正方体木箱中,想放入一根细长的直钢管,则这根钢管的最大长度可以是________.
4.给出下列运算:①,② =±4,③ =-2,④,⑤= .其中,错误的有( ).
(A)2个 (B)3个 (C)4个 (D)5个
5.算术平方根等于它本身的数有________,立方根等于本身的数有________.
6.若,则________,若,则________.
7.已知两边为3,4,则第三边长________.
8.如果+(y+6)2=0,则________.
9.如果和是一个数的平方根,则
10.下面条件中,能判定四边形ABCD是平行四边形的有( )
(1)∠A=∠B,∠C=∠D;(2)AB∥CD ,AB=CD;(3)AB∥CD ,AD=BC ;(4)AB=CD,AD=CB;(5)AB∥CD ,∠A=∠C。
A. 1 B. 2 C. 3 D. 4
11.已知如图所示,四边形ABCD 求四边形ABCD的面积.
12.在一张纸上画两个全等的直角三角形,并把它们拼成如图形状,请用两种方法表示这个梯形的面积。利用你的表示方法,你能得到勾股定理吗?
13.已知:与互为相反数,求(2x-y)2 的平方根。
14.如图,某菜农要修建一个育苗棚,棚宽a=12m,高b=5m,长d=20m,请你帮他算一下覆盖在顶上的塑料薄膜需多少?
15.如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积。
16.如图,A,B是直线l外同侧的两点,且点A和点B到l的距离分别是3㎝和5㎝,AB=12㎝,若点P在l上移动,
求PA+PB的最小值。
【布置作业】
《补充习题》同步练习
① ② ③ ④ ⑤
第1题
400
64
A
400
图4
图3
…
…
A
C
B
1
C
A
0
B
0
B
A
C
A
B
C
D
F
E
A
D
B
C
E
A
D
O
B
C
64
A
·B
·A
l
x
x
1
1
1
x
PAGE
32
主备人:顾风金 审核人:朱刚
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
