等差数列的前n项和
图片预览





文档简介
课件15张PPT。等差数列的前n项和公式
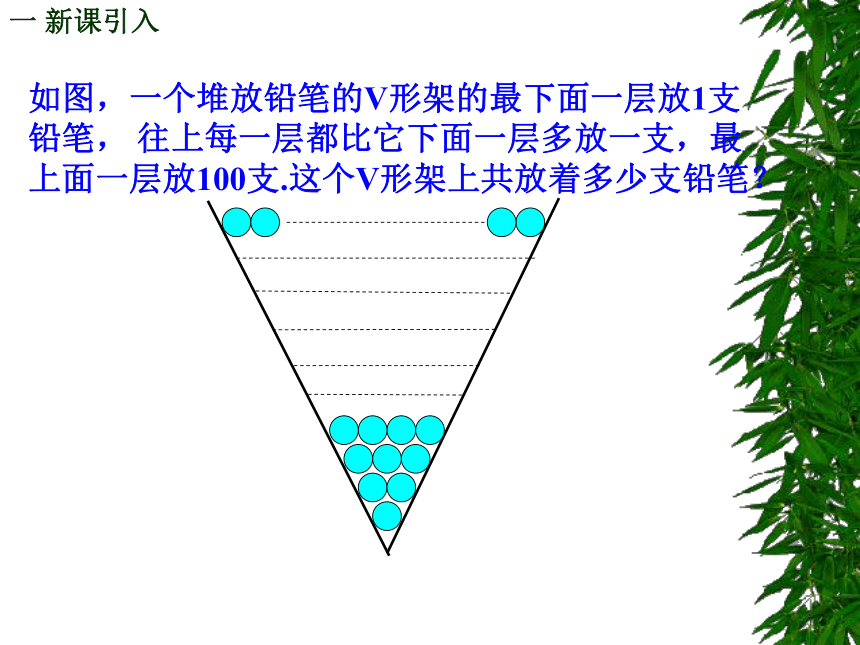
如图,一个堆放铅笔的V形架的最下面一层放1支
铅笔, 往上每一层都比它下面一层多放一支,最
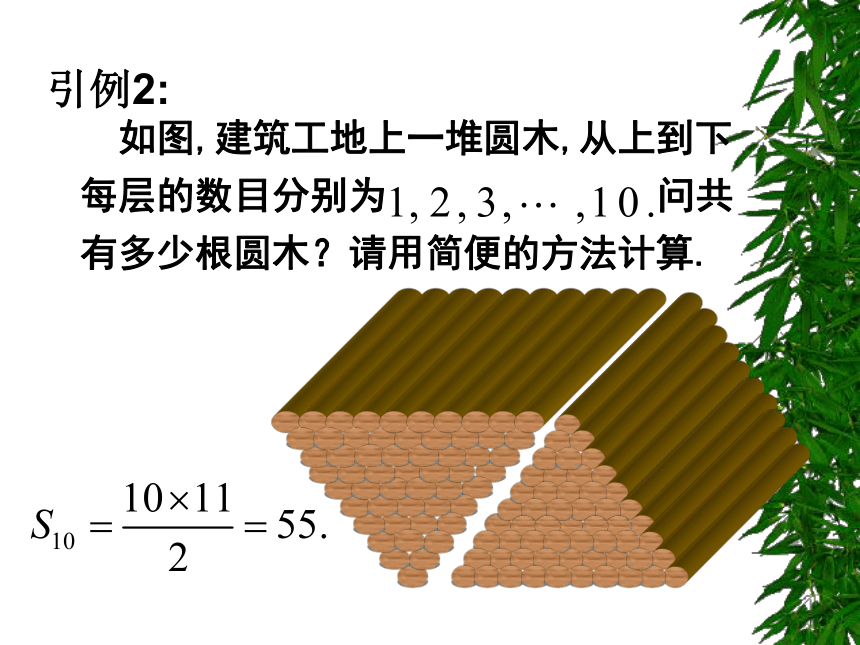
上面一层放100支.这个V形架上共放着多少支铅笔?一 新课引入问题就是 “ ” 高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,…,每组数的和均相等,都等于101,50个101就等于5050了.高斯算法将加法问题转化为乘法运算,迅速准确得到了结果. 如图,建筑工地上一堆圆木,从上到下
每层的数目分别为 问共
有多少根圆木?请用简便的方法计算.引例2:二.讲解新课 1.公式推导问题:设等差数列 的首项为 ,公差为 ,又等差数列 的前 项和 满足:公式推导:而2.公式记忆 用梯形面积公式记忆等差数列前n项和公式,这里对图形进行了割、补两种处理,对应着等差数列前 n项和的两个公式.已知数列 为等差数列.
(1)设 求例1解析:(2)设 求解析:3.公式的应用P45练习1例2解析:由 已知一个等差数列的前 项和
前 项 由此可以确定其前
项的 的公式吗?S练习:
(2) (结果用 表示)2.等差数列 中前多少项的和是9900?例3解析: 已知数列 的前 项和为
(1)求数列 的通项公式;
(2)求证:数列 是等差数列.练习:
P45练习21.推导等差数列前 项和公式的思路;
2.公式的应用中的数学思想. 三.小结
如图,一个堆放铅笔的V形架的最下面一层放1支
铅笔, 往上每一层都比它下面一层多放一支,最
上面一层放100支.这个V形架上共放着多少支铅笔?一 新课引入问题就是 “ ” 高斯算法的高明之处在于他发现这100个数可以分为50组,第一个数与最后一个数一组,第二个数与倒数第二个数一组,第三个数与倒数第三个数一组,…,每组数的和均相等,都等于101,50个101就等于5050了.高斯算法将加法问题转化为乘法运算,迅速准确得到了结果. 如图,建筑工地上一堆圆木,从上到下
每层的数目分别为 问共
有多少根圆木?请用简便的方法计算.引例2:二.讲解新课 1.公式推导问题:设等差数列 的首项为 ,公差为 ,又等差数列 的前 项和 满足:公式推导:而2.公式记忆 用梯形面积公式记忆等差数列前n项和公式,这里对图形进行了割、补两种处理,对应着等差数列前 n项和的两个公式.已知数列 为等差数列.
(1)设 求例1解析:(2)设 求解析:3.公式的应用P45练习1例2解析:由 已知一个等差数列的前 项和
前 项 由此可以确定其前
项的 的公式吗?S练习:
(2) (结果用 表示)2.等差数列 中前多少项的和是9900?例3解析: 已知数列 的前 项和为
(1)求数列 的通项公式;
(2)求证:数列 是等差数列.练习:
P45练习21.推导等差数列前 项和公式的思路;
2.公式的应用中的数学思想. 三.小结
