上海市嘉定区2021-2022学年七年级(下)期末数学试卷(word版含解析)
文档属性
| 名称 | 上海市嘉定区2021-2022学年七年级(下)期末数学试卷(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 140.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 17:32:18 | ||
图片预览



文档简介
上海市嘉定区2021-2022学年七年级(下)期末数学试卷
一 、单选题(本大题共6小题,共24分)
1.(4分)下列四个实数中,是无理数的是
A. B. C. D.
2.(4分)实数,,在数轴上对应点的位置如图所示,若,则下列结论中正确的是
A. B. C. D.
3.(4分)在平面直角坐标系中,将点向左平移个单位,再向上平移个单位,则平移后的点的坐标是
A. B. C. D.
4.(4分)如图,和是同位角的图形有
A. ③④ B. ①③⑤ C. ①②⑤ D. ①②③
5.(4分)如图,,,要使,下列补充的条件正确的个数有
①;
②;
③;
④
A. 个 B. 个 C. 个 D. 个
6.(4分)如图,,添加下列条件仍不能判定的是
A. B. C. D.
二 、填空题(本大题共14小题,共52分)
7.(4分)如果,则______.
8.(4分)______,______.
9.(4分)比较大小:______填“”,“”或“”
10.(4分)把写成幂的形式是 ______ .
11.(4分)已知:实数,在数轴上的位置如图所示,化简:为 ______ .
12.(4分)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距千米,用科学记数法表示这个数并保留三个有效数字是 ______千米.
13.(4分)在平面直角坐标系中,若与点关于轴对称,则______.
14.(4分)在平面直角坐标系中,将点先向上平移个单位长度,再向左平移个单位长度后得到的点的坐标是 ______.
15.(4分)(2019-2020二中广雅训练卷)若∠A的两边分别与∠B的两边平行,且∠A比∠B的3倍少60°,则∠A的度数为_______________.
16.(4分)如图,在中,,,,分别是角平分线和高,则的度数是 ______.
17.(3分)如图所示,已知平分,平分,过点的直线,若,,,则的周长为______.
18.(3分)在等腰中,,顶角的度数是,则它的一个底角的度数为 ______.
19.(3分)如图,,、交于点,三角形的面积等于,三角形的面积等于,那么三角形的面积等于 ______.
20.(3分)右图中,点的坐标为,点的坐标为,如果要使与全等点不与点重合,那么点的坐标是 ______.
三 、解答题(本大题共8小题,共24分)
21.(3分)计算:
22.(3分)计算
;
;
23.(3分)
24.(3分)如图,射线与直线相交于,在射线的右侧分别过点,作射线,,且平分,
求证:;
是射线上的一点,平分,连接,的平分线交直线于点
①如备用图,若,求证:;
②如备用图,若,,,求的值.用含的式子表示
25.(3分)如图,在边长为的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点为原点,点、的坐标分别是,
将绕点逆时针旋转后得到,请在图中画出,并求出这时点的坐标为 ______;
旋转后的面积为 ______;
计算在旋转过程中,线段扫过的图形的弧长.
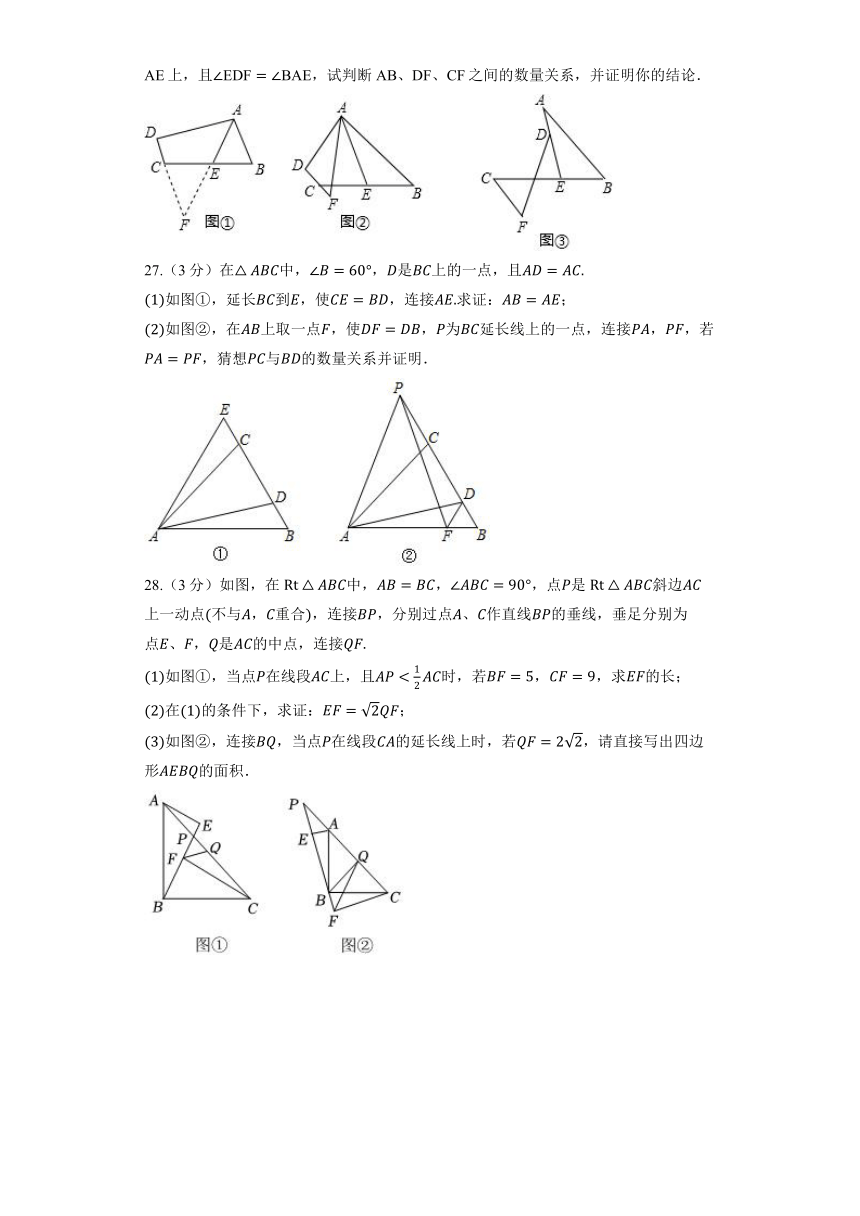
26.(3分)阅读理解:如图,在四边形中,,是的中点,若是的平分线,试判断,,之间的等量关系.
解决此问题可以用如下方法:延长交的延长线于点,易证≌,得到,从而把,,转化在一个三角形中即可判断.
、、之间的等量关系为______;
问题探究:如图,在四边形中,,与的延长线交于点,是的中点,若是的平分线,试探究,,之间的等量关系,并证明你的结论.
问题解决:如图,,与交于点,::,点在线段上,且,试判断、、之间的数量关系,并证明你的结论.
27.(3分)在中,,是上的一点,且
如图①,延长到,使,连接求证:;
如图②,在上取一点,使,为延长线上的一点,连接,,若,猜想与的数量关系并证明.
28.(3分)如图,在中,,,点是斜边上一动点不与,重合,连接,分别过点、作直线的垂线,垂足分别为点、,是的中点,连接
如图①,当点在线段上,且时,若,,求的长;
在的条件下,求证:;
如图②,连接,当点在线段的延长线上时,若,请直接写出四边形的面积.
答案和解析
1.【答案】B;
【解析】解:、是有限小数,属于有理数,故此选项不符合题意;
、是无理数,故此选项符合题意;
、,是整数,属于有理数,故此选项不符合题意;
、是分数,属于有理数,故此选项不符合题意.
故选:
分别根据无理数、有理数的定义即可判定选择项.
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如,,…每两个之间依次多个等形式.
2.【答案】C;
【解析】解:,
原点在,的中间,
如图:
由图可得:,
,,,,
故选项正确.
故选:
根据,确定原点的位置,根据实数与数轴即可解答.
此题主要考查了实数与数轴,解决本题的关键是确定原点的位置.
3.【答案】C;
【解析】解:将点向左平移个单位,再向上平移个单位,
则平移后的点的坐标是,
即,
故选:
根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得答案.
此题主要考查了点的坐标,解答该题的关键是掌握点的坐标与图形的平移的关系.
4.【答案】C;
【解析】解:根据同位角定义可得①②⑤是同位角,
故选:
根据同位角的定义:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线截线的同旁,则这样一对角叫做同位角进行分析即可.
此题主要考查了同位角,解答该题的关键是掌握同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
5.【答案】C;
【解析】解:,
,
即,
,
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,根据“”可判断
故选:
先证明,然后根据全等三角形的判定方法对添加的四个条件进行判断.
此题主要考查了全等三角形的判定:熟练掌握全等三角形的种判定方法是解决问题的关键.选用哪一种方法,取决于题目中的已知条件.
6.【答案】B;
【解析】解:,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
B.,,,不符合全等三角形的判定定理,不能推出,故本选项符合题意;
C.,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
D.,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
故选:
根据全等三角形的判定定理逐个判断即可.
此题主要考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有,,,,两直角三角形全等还有等.
7.【答案】±5;
【解析】解:,
,
故答案为:
根据平方根的定义求出即可.
此题主要考查了对平方根定义的应用,注意:的平方根是
8.【答案】-2 ;
【解析】解:,
故答案为:,
根据有理数的平方和立方根的定义即可求出答案.
此题主要考查有理数的平方和立方根,解答该题的关键是正确理解负数的平方是正数,本题属于基础题型.
9.【答案】<;
【解析】解:,,
,
,
故答案为:
先求出这两个数的平方,然后再进行比较即可.
此题主要考查了实数大小比较,算术平方根,熟练掌握平方运算比较大小是解答该题的关键.
10.【答案】;
【解析】解:,
故答案为:
根据分数指数幂公式,逆推即可得到答案.
此题主要考查了分数指数幂,正确理解分数指数幂的含义以及会逆向推理是解答该题的关键.
11.【答案】;
【解析】【分析】
本题考查了数轴,绝对值,二次根式的性质的应用,难度一般.
根据数轴得出,求出,,,根据二次根式的性质和绝对值把变成,求出即可.
【解答】解:从数轴可知:,
,,,
.
故答案为.
12.【答案】4.05×105;
【解析】解:千米千米千米.
故答案为:
科学记数法的表示形式为的形式.其中,为整数.用科学记数法表示的数的有效数字只与前面的有关,与的多少次方无关.
此题主要考查科学记数法的表示方法,科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
13.【答案】1;
【解析】解:点与点关于轴对称,
,,
解得:,,
故答案为:
关于轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.直接利用关于轴对称点的性质得出,的值,进而得出答案.
此题主要考查了关于轴对称点的特征,点关于轴的对称点的坐标是
14.【答案】(-6,1);
【解析】解:点先向上平移个单位,再向左平移个单位,得到点的坐标是,即,
故答案为:
根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点的坐标是,进而可得答案.
此题主要考查了坐标与图形的变化,关键是掌握点的坐标的变化规律.
15.【答案】230°或120°;
【解析】解:∠A与∠B相等或互补,当∠A=∠B时,∠A=30°;
当∠A与∠B互补,∠A=120°.
16.【答案】10°;
【解析】解:,,
,
是的角平分线,
,
又是的高,
,
,
故答案为:
利用三角形内角和定理求出,再根据角平分线和高线,可求出和,进而可求出的度数.
此题主要考查了三角形的内角和定理、角平分线的性质等知识点,掌握三角形的内角和定理是解题关键.
17.【答案】26;
【解析】解:平分,平分,
,,
,
,,
,,
,,
的周长,
故答案为:
根据平行线的性质和角平分线的定义得出,进而得出,同理得出,进而解答即可.
此题主要考查等腰三角形的判定和性质,关键是根据平行线的性质和角平分线的定义得出
18.【答案】75°;
【解析】解:,顶角的度数是,
,
故答案为:
根据三角形的内角和顶角的度数求得底角的度数即可.
考查了等腰三角形的性质,解答该题的关键是了解等腰三角形的两个底角相等,难度不大.
19.【答案】9;
【解析】解:,
,
,
,
故答案为:
由得,可得,从而可得出结果.
此题主要考查了三角形的面积,利用同底等高求解是解答该题的关键.
20.【答案】(4,-1)或(-1,3)或(-1,-1);
【解析】解:符合题意的有个,如图,
点、、坐标为,,,
的坐标是,的坐标是,的坐标是,
故答案为:或或
根据题意画出图形,根据、、的坐标和全等三角形的性质即可得出答案.
此题主要考查了全等三角形的性质和坐标与图形性质的应用,注意要考虑全面,不要漏解.
21.【答案】解:原式=-2+1+
=-2.;
【解析】
根据立方根、平方根以及零次幂、负整数指数幂的意义计算.
此题主要考查了实数的混合运算运算,正确理解平方根与立方根的意义是解答该题的关键.
22.【答案】解:(1)原式=
=
=;
(2)原式=4-+
=;
(3)原式=(9-2)-(3+)
=4-.;
【解析】
根据二次根式的乘法法则和除法法则运算;
先把二次根式化为最简二次根式,然后合并即可;
利用平方差公式和完全平方公式计算.
此题主要考查了二次根式的混合运算,熟练掌握二次根式的乘除法法则和乘法公式是解决问题的关键.
23.【答案】解:-++
=12-(-3)+8+2
=25.;
【解析】
首先计算分数指数幂、负整数指数幂和开方,然后从左向右依次计算,求出算式的值是多少即可.
此题主要考查了实数的运算,要熟练掌握,解答该题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
24.【答案】(1)证明:∵CE平分∠DCG,
∴∠DCG=2∠ECG,
∵∠A=2∠ACF,∠ACF=∠ECG,
∴∠A=∠DCG,
∴AB∥CD.
(2)①证明:∵AB∥CD,HI∥AG,
∴∠A+∠ACD=180°,∠A+∠AHI=180°,
∴∠ACD=∠AHI,
∵CI平分∠ACD,HK平分∠AHI,
∴∠DCI=∠ACD,∠AHK=∠AHI,
∴∠DCI=∠AHK.
②解:∵AB∥CD,
∴∠DCG=∠A=α,∠ACD=180°-∠A=180°-α,
∵∠BHI=β,
∴∠AHI=180°-∠BHI=180°-β.
∵CE平分∠DCG,CI平分∠ACD,HK平分∠AHI,
∴∠DCE=∠DCG=α,∠DCI=∠ACD=(180°-α)=90°-α,
∠AHK=∠AHI=(180°-β)=90°-β.
过点K作KM∥AB,过点I作IN∥AB,
∴KM∥AB∥CD,IN∥AB∥CD,
∴∠CKM=∠DCE,∠HKM=∠AHK,∠DCI=∠CIN,∠NIH=∠BHI,
∴∠HKC=α+90°-β,∠HIC=90°-α+β.
∵∠HKC=∠HIC,
∴α+90°-β=90°-α+β,
∴α=.;
【解析】
结合已知条件,利用平行线的判定定理即可求证.
①①由,,可得,,进而可得,再结合角平分线的定义即可证明.
②过点作,过点作,结合平行线的性质和角平分线的定义,分别用含和的代数式表示和,建立方程,可得
此题主要考查平行线的判定与性质、角平分线的定义,熟练掌握平行线的判定与性质是解答本题的关键.
25.【答案】(-3,1) 3.5;
【解析】解:如图,即为所求.并求出这时点的坐标为
故答案为:;
旋转后的面积
故答案为:;
,
线段扫过的图形的弧长
根据旋转变换的性质分别作出,的对应点,即可;
把三角形的面积看成矩形的面积减去周围的三个三角形面积即可;
利用勾股定理求出,再利用弧长公式求解.
此题主要考查作图旋转变换,弧长公式,三角形的面积等知识,解答该题的关键是掌握旋转变换的性质,记住弧长公式
26.【答案】解:;
,
证明:如图,延长交的延长线于点,
是的中点,
,
,
,
在和中,
,
≌,
,
是的平分线,
,
,
,
,
,
;
,
证明:如图,延长交的延长线于点,
,
∽,
,即,
,
,
,
,
,
.
;
【解析】解:如图,延长交的延长线于点,
,
,
是的中点,
,
在和中,
,
≌,
,
是的平分线,
,
,
,
,
故答案为:;
见答案;
见答案.
延长交的延长线于点,证明≌,根据全等三角形的性质得到,根据等腰三角形的判定得到,证明结论;
延长交的延长线于点,利用同相同的方法证明;
延长交的延长线于点,根据相似三角形的判定定理得到∽,根据相似三角形的性质得到,计算即可.
该题考查的是全等三角形的判定和性质、相似三角形的判定和性质,正确作出辅助性、灵活运用相关的性质定理和判定定理是解答该题的关键.
27.【答案】证明:在中,,
,
,
在和中,
,
,
;
解:与的数量关系为:,理由如下:
在线段上取一点,使,连接,如图②所示:
由得:,
,
,
,,
是等边三角形,
,
,,
,
,
,
,
,
在和中,
,
,
,
;
【解析】
证,即可得出结论;
在线段上取一点,使,连接,由得,则,再证是等边三角形,得,然后证,得,即可得出结论.
此题主要考查了全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的性质等知识,熟练掌握等腰三角形的性质,证明三角形全等是解答该题的关键.
28.【答案】(1)解:∵AE⊥BE,BF⊥BE,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠CBE=90°=∠ABE+∠BAE,
∴∠BAE=∠CBE,
又∵AB=BC,∠AEB=∠BFC=90°,
∴△ABE≌△BCF(AAS),
∴CF=BE=9,AE=BF,
∴EF=BE-BF=9-5=4;
(2)证明:如图①,连接EQ,并延长交CF于K,
∵点Q是AC的中点,
∴AQ=CQ,
∵AE⊥BE,BF⊥BE,
∴AE∥CF,
∴∠EAQ=∠KCQ,
又∵∠AQE=∠CQK,AQ=CQ,
∴△AQE≌△CQK(ASA),
∴EQ=QK,CK=AE,
∴AE=BF=CK,
∴EF=FK,
又∵∠EFK=90°,EQ=QK,
∴FQ=EQ,FQ⊥EK,
∴EF=QF;
(3)解:如图②,过点Q作QH⊥BE于H,QN⊥CF于N,
同理可证△ABE≌△BCF(AAS),
∴S△ABE=S△BCF,
∵AB=BC,∠ABC=90°,点Q在AC的中点,
∴BQ=AQ=CQ,∠AQB=∠CQB=90°,∠ACB=∠CBQ=45°,
∴△ABQ≌△CBQ(SAS),
∴S△ABQ=S△CBQ,
∴S四边形AEBQ=S四边形BQCF,
∵QH⊥BE,QN⊥CF,∠CFB=90°,
∴四边形FNQH是矩形,
∵∠CFB=∠BQC=90°,
∴点B,点Q,点C,点F四点共圆,
∴∠QFC=∠QBC=45°,∠QCB=∠QFB=45°,
∴∠QFB=∠QFC=45°,
又∵QH⊥BE,QN⊥CF,
∴QH=QN,
∴四边形FNQH是正方形,
∴QF=QN=2,
∴QN=2,
∵∠CFB=∠BQC=90°,
∴∠QCF+∠QBF=180°,
又∵∠QBE+∠QBF=180°,
∴∠QCF=∠QBH,
又∵QH=QN,∠QHB=∠QNC=90°,
∴△QBH≌△QCN(AAS),
∴S△QBH=S△QCN,
∴S四边形AEBQ=S四边形BQCF=S正方形FNQH=4.;
【解析】
由“”可证,可得,即可求解;
由“”可证,,由等腰直角三角形的性质可得结论;
由全等三角形的性质和等腰直角三角形的性质,可证,即可求解.
本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,正方形的判定和性质等知识,添加恰当辅助线构造全等三角形是解答该题的关键.
一 、单选题(本大题共6小题,共24分)
1.(4分)下列四个实数中,是无理数的是
A. B. C. D.
2.(4分)实数,,在数轴上对应点的位置如图所示,若,则下列结论中正确的是
A. B. C. D.
3.(4分)在平面直角坐标系中,将点向左平移个单位,再向上平移个单位,则平移后的点的坐标是
A. B. C. D.
4.(4分)如图,和是同位角的图形有
A. ③④ B. ①③⑤ C. ①②⑤ D. ①②③
5.(4分)如图,,,要使,下列补充的条件正确的个数有
①;
②;
③;
④
A. 个 B. 个 C. 个 D. 个
6.(4分)如图,,添加下列条件仍不能判定的是
A. B. C. D.
二 、填空题(本大题共14小题,共52分)
7.(4分)如果,则______.
8.(4分)______,______.
9.(4分)比较大小:______填“”,“”或“”
10.(4分)把写成幂的形式是 ______ .
11.(4分)已知:实数,在数轴上的位置如图所示,化简:为 ______ .
12.(4分)月球沿着一定的轨道围绕地球运动,某一时刻它与地球相距千米,用科学记数法表示这个数并保留三个有效数字是 ______千米.
13.(4分)在平面直角坐标系中,若与点关于轴对称,则______.
14.(4分)在平面直角坐标系中,将点先向上平移个单位长度,再向左平移个单位长度后得到的点的坐标是 ______.
15.(4分)(2019-2020二中广雅训练卷)若∠A的两边分别与∠B的两边平行,且∠A比∠B的3倍少60°,则∠A的度数为_______________.
16.(4分)如图,在中,,,,分别是角平分线和高,则的度数是 ______.
17.(3分)如图所示,已知平分,平分,过点的直线,若,,,则的周长为______.
18.(3分)在等腰中,,顶角的度数是,则它的一个底角的度数为 ______.
19.(3分)如图,,、交于点,三角形的面积等于,三角形的面积等于,那么三角形的面积等于 ______.
20.(3分)右图中,点的坐标为,点的坐标为,如果要使与全等点不与点重合,那么点的坐标是 ______.
三 、解答题(本大题共8小题,共24分)
21.(3分)计算:
22.(3分)计算
;
;
23.(3分)
24.(3分)如图,射线与直线相交于,在射线的右侧分别过点,作射线,,且平分,
求证:;
是射线上的一点,平分,连接,的平分线交直线于点
①如备用图,若,求证:;
②如备用图,若,,,求的值.用含的式子表示
25.(3分)如图,在边长为的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点为原点,点、的坐标分别是,
将绕点逆时针旋转后得到,请在图中画出,并求出这时点的坐标为 ______;
旋转后的面积为 ______;
计算在旋转过程中,线段扫过的图形的弧长.
26.(3分)阅读理解:如图,在四边形中,,是的中点,若是的平分线,试判断,,之间的等量关系.
解决此问题可以用如下方法:延长交的延长线于点,易证≌,得到,从而把,,转化在一个三角形中即可判断.
、、之间的等量关系为______;
问题探究:如图,在四边形中,,与的延长线交于点,是的中点,若是的平分线,试探究,,之间的等量关系,并证明你的结论.
问题解决:如图,,与交于点,::,点在线段上,且,试判断、、之间的数量关系,并证明你的结论.
27.(3分)在中,,是上的一点,且
如图①,延长到,使,连接求证:;
如图②,在上取一点,使,为延长线上的一点,连接,,若,猜想与的数量关系并证明.
28.(3分)如图,在中,,,点是斜边上一动点不与,重合,连接,分别过点、作直线的垂线,垂足分别为点、,是的中点,连接
如图①,当点在线段上,且时,若,,求的长;
在的条件下,求证:;
如图②,连接,当点在线段的延长线上时,若,请直接写出四边形的面积.
答案和解析
1.【答案】B;
【解析】解:、是有限小数,属于有理数,故此选项不符合题意;
、是无理数,故此选项符合题意;
、,是整数,属于有理数,故此选项不符合题意;
、是分数,属于有理数,故此选项不符合题意.
故选:
分别根据无理数、有理数的定义即可判定选择项.
此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如,,…每两个之间依次多个等形式.
2.【答案】C;
【解析】解:,
原点在,的中间,
如图:
由图可得:,
,,,,
故选项正确.
故选:
根据,确定原点的位置,根据实数与数轴即可解答.
此题主要考查了实数与数轴,解决本题的关键是确定原点的位置.
3.【答案】C;
【解析】解:将点向左平移个单位,再向上平移个单位,
则平移后的点的坐标是,
即,
故选:
根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得答案.
此题主要考查了点的坐标,解答该题的关键是掌握点的坐标与图形的平移的关系.
4.【答案】C;
【解析】解:根据同位角定义可得①②⑤是同位角,
故选:
根据同位角的定义:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线截线的同旁,则这样一对角叫做同位角进行分析即可.
此题主要考查了同位角,解答该题的关键是掌握同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
5.【答案】C;
【解析】解:,
,
即,
,
当添加时,根据“”可判断;
当添加时,根据“”可判断;
当添加时,根据“”可判断
故选:
先证明,然后根据全等三角形的判定方法对添加的四个条件进行判断.
此题主要考查了全等三角形的判定:熟练掌握全等三角形的种判定方法是解决问题的关键.选用哪一种方法,取决于题目中的已知条件.
6.【答案】B;
【解析】解:,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
B.,,,不符合全等三角形的判定定理,不能推出,故本选项符合题意;
C.,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
D.,,,符合全等三角形的判定定理,能推出,故本选项不符合题意;
故选:
根据全等三角形的判定定理逐个判断即可.
此题主要考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有,,,,两直角三角形全等还有等.
7.【答案】±5;
【解析】解:,
,
故答案为:
根据平方根的定义求出即可.
此题主要考查了对平方根定义的应用,注意:的平方根是
8.【答案】-2 ;
【解析】解:,
故答案为:,
根据有理数的平方和立方根的定义即可求出答案.
此题主要考查有理数的平方和立方根,解答该题的关键是正确理解负数的平方是正数,本题属于基础题型.
9.【答案】<;
【解析】解:,,
,
,
故答案为:
先求出这两个数的平方,然后再进行比较即可.
此题主要考查了实数大小比较,算术平方根,熟练掌握平方运算比较大小是解答该题的关键.
10.【答案】;
【解析】解:,
故答案为:
根据分数指数幂公式,逆推即可得到答案.
此题主要考查了分数指数幂,正确理解分数指数幂的含义以及会逆向推理是解答该题的关键.
11.【答案】;
【解析】【分析】
本题考查了数轴,绝对值,二次根式的性质的应用,难度一般.
根据数轴得出,求出,,,根据二次根式的性质和绝对值把变成,求出即可.
【解答】解:从数轴可知:,
,,,
.
故答案为.
12.【答案】4.05×105;
【解析】解:千米千米千米.
故答案为:
科学记数法的表示形式为的形式.其中,为整数.用科学记数法表示的数的有效数字只与前面的有关,与的多少次方无关.
此题主要考查科学记数法的表示方法,科学记数法的表示形式为的形式,其中,为整数,表示时关键要正确确定的值以及的值.
13.【答案】1;
【解析】解:点与点关于轴对称,
,,
解得:,,
故答案为:
关于轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变.直接利用关于轴对称点的性质得出,的值,进而得出答案.
此题主要考查了关于轴对称点的特征,点关于轴的对称点的坐标是
14.【答案】(-6,1);
【解析】解:点先向上平移个单位,再向左平移个单位,得到点的坐标是,即,
故答案为:
根据横坐标,右移加,左移减;纵坐标,上移加,下移减可得点的坐标是,进而可得答案.
此题主要考查了坐标与图形的变化,关键是掌握点的坐标的变化规律.
15.【答案】230°或120°;
【解析】解:∠A与∠B相等或互补,当∠A=∠B时,∠A=30°;
当∠A与∠B互补,∠A=120°.
16.【答案】10°;
【解析】解:,,
,
是的角平分线,
,
又是的高,
,
,
故答案为:
利用三角形内角和定理求出,再根据角平分线和高线,可求出和,进而可求出的度数.
此题主要考查了三角形的内角和定理、角平分线的性质等知识点,掌握三角形的内角和定理是解题关键.
17.【答案】26;
【解析】解:平分,平分,
,,
,
,,
,,
,,
的周长,
故答案为:
根据平行线的性质和角平分线的定义得出,进而得出,同理得出,进而解答即可.
此题主要考查等腰三角形的判定和性质,关键是根据平行线的性质和角平分线的定义得出
18.【答案】75°;
【解析】解:,顶角的度数是,
,
故答案为:
根据三角形的内角和顶角的度数求得底角的度数即可.
考查了等腰三角形的性质,解答该题的关键是了解等腰三角形的两个底角相等,难度不大.
19.【答案】9;
【解析】解:,
,
,
,
故答案为:
由得,可得,从而可得出结果.
此题主要考查了三角形的面积,利用同底等高求解是解答该题的关键.
20.【答案】(4,-1)或(-1,3)或(-1,-1);
【解析】解:符合题意的有个,如图,
点、、坐标为,,,
的坐标是,的坐标是,的坐标是,
故答案为:或或
根据题意画出图形,根据、、的坐标和全等三角形的性质即可得出答案.
此题主要考查了全等三角形的性质和坐标与图形性质的应用,注意要考虑全面,不要漏解.
21.【答案】解:原式=-2+1+
=-2.;
【解析】
根据立方根、平方根以及零次幂、负整数指数幂的意义计算.
此题主要考查了实数的混合运算运算,正确理解平方根与立方根的意义是解答该题的关键.
22.【答案】解:(1)原式=
=
=;
(2)原式=4-+
=;
(3)原式=(9-2)-(3+)
=4-.;
【解析】
根据二次根式的乘法法则和除法法则运算;
先把二次根式化为最简二次根式,然后合并即可;
利用平方差公式和完全平方公式计算.
此题主要考查了二次根式的混合运算,熟练掌握二次根式的乘除法法则和乘法公式是解决问题的关键.
23.【答案】解:-++
=12-(-3)+8+2
=25.;
【解析】
首先计算分数指数幂、负整数指数幂和开方,然后从左向右依次计算,求出算式的值是多少即可.
此题主要考查了实数的运算,要熟练掌握,解答该题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.
24.【答案】(1)证明:∵CE平分∠DCG,
∴∠DCG=2∠ECG,
∵∠A=2∠ACF,∠ACF=∠ECG,
∴∠A=∠DCG,
∴AB∥CD.
(2)①证明:∵AB∥CD,HI∥AG,
∴∠A+∠ACD=180°,∠A+∠AHI=180°,
∴∠ACD=∠AHI,
∵CI平分∠ACD,HK平分∠AHI,
∴∠DCI=∠ACD,∠AHK=∠AHI,
∴∠DCI=∠AHK.
②解:∵AB∥CD,
∴∠DCG=∠A=α,∠ACD=180°-∠A=180°-α,
∵∠BHI=β,
∴∠AHI=180°-∠BHI=180°-β.
∵CE平分∠DCG,CI平分∠ACD,HK平分∠AHI,
∴∠DCE=∠DCG=α,∠DCI=∠ACD=(180°-α)=90°-α,
∠AHK=∠AHI=(180°-β)=90°-β.
过点K作KM∥AB,过点I作IN∥AB,
∴KM∥AB∥CD,IN∥AB∥CD,
∴∠CKM=∠DCE,∠HKM=∠AHK,∠DCI=∠CIN,∠NIH=∠BHI,
∴∠HKC=α+90°-β,∠HIC=90°-α+β.
∵∠HKC=∠HIC,
∴α+90°-β=90°-α+β,
∴α=.;
【解析】
结合已知条件,利用平行线的判定定理即可求证.
①①由,,可得,,进而可得,再结合角平分线的定义即可证明.
②过点作,过点作,结合平行线的性质和角平分线的定义,分别用含和的代数式表示和,建立方程,可得
此题主要考查平行线的判定与性质、角平分线的定义,熟练掌握平行线的判定与性质是解答本题的关键.
25.【答案】(-3,1) 3.5;
【解析】解:如图,即为所求.并求出这时点的坐标为
故答案为:;
旋转后的面积
故答案为:;
,
线段扫过的图形的弧长
根据旋转变换的性质分别作出,的对应点,即可;
把三角形的面积看成矩形的面积减去周围的三个三角形面积即可;
利用勾股定理求出,再利用弧长公式求解.
此题主要考查作图旋转变换,弧长公式,三角形的面积等知识,解答该题的关键是掌握旋转变换的性质,记住弧长公式
26.【答案】解:;
,
证明:如图,延长交的延长线于点,
是的中点,
,
,
,
在和中,
,
≌,
,
是的平分线,
,
,
,
,
,
;
,
证明:如图,延长交的延长线于点,
,
∽,
,即,
,
,
,
,
,
.
;
【解析】解:如图,延长交的延长线于点,
,
,
是的中点,
,
在和中,
,
≌,
,
是的平分线,
,
,
,
,
故答案为:;
见答案;
见答案.
延长交的延长线于点,证明≌,根据全等三角形的性质得到,根据等腰三角形的判定得到,证明结论;
延长交的延长线于点,利用同相同的方法证明;
延长交的延长线于点,根据相似三角形的判定定理得到∽,根据相似三角形的性质得到,计算即可.
该题考查的是全等三角形的判定和性质、相似三角形的判定和性质,正确作出辅助性、灵活运用相关的性质定理和判定定理是解答该题的关键.
27.【答案】证明:在中,,
,
,
在和中,
,
,
;
解:与的数量关系为:,理由如下:
在线段上取一点,使,连接,如图②所示:
由得:,
,
,
,,
是等边三角形,
,
,,
,
,
,
,
,
在和中,
,
,
,
;
【解析】
证,即可得出结论;
在线段上取一点,使,连接,由得,则,再证是等边三角形,得,然后证,得,即可得出结论.
此题主要考查了全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的性质等知识,熟练掌握等腰三角形的性质,证明三角形全等是解答该题的关键.
28.【答案】(1)解:∵AE⊥BE,BF⊥BE,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠CBE=90°=∠ABE+∠BAE,
∴∠BAE=∠CBE,
又∵AB=BC,∠AEB=∠BFC=90°,
∴△ABE≌△BCF(AAS),
∴CF=BE=9,AE=BF,
∴EF=BE-BF=9-5=4;
(2)证明:如图①,连接EQ,并延长交CF于K,
∵点Q是AC的中点,
∴AQ=CQ,
∵AE⊥BE,BF⊥BE,
∴AE∥CF,
∴∠EAQ=∠KCQ,
又∵∠AQE=∠CQK,AQ=CQ,
∴△AQE≌△CQK(ASA),
∴EQ=QK,CK=AE,
∴AE=BF=CK,
∴EF=FK,
又∵∠EFK=90°,EQ=QK,
∴FQ=EQ,FQ⊥EK,
∴EF=QF;
(3)解:如图②,过点Q作QH⊥BE于H,QN⊥CF于N,
同理可证△ABE≌△BCF(AAS),
∴S△ABE=S△BCF,
∵AB=BC,∠ABC=90°,点Q在AC的中点,
∴BQ=AQ=CQ,∠AQB=∠CQB=90°,∠ACB=∠CBQ=45°,
∴△ABQ≌△CBQ(SAS),
∴S△ABQ=S△CBQ,
∴S四边形AEBQ=S四边形BQCF,
∵QH⊥BE,QN⊥CF,∠CFB=90°,
∴四边形FNQH是矩形,
∵∠CFB=∠BQC=90°,
∴点B,点Q,点C,点F四点共圆,
∴∠QFC=∠QBC=45°,∠QCB=∠QFB=45°,
∴∠QFB=∠QFC=45°,
又∵QH⊥BE,QN⊥CF,
∴QH=QN,
∴四边形FNQH是正方形,
∴QF=QN=2,
∴QN=2,
∵∠CFB=∠BQC=90°,
∴∠QCF+∠QBF=180°,
又∵∠QBE+∠QBF=180°,
∴∠QCF=∠QBH,
又∵QH=QN,∠QHB=∠QNC=90°,
∴△QBH≌△QCN(AAS),
∴S△QBH=S△QCN,
∴S四边形AEBQ=S四边形BQCF=S正方形FNQH=4.;
【解析】
由“”可证,可得,即可求解;
由“”可证,,由等腰直角三角形的性质可得结论;
由全等三角形的性质和等腰直角三角形的性质,可证,即可求解.
本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,正方形的判定和性质等知识,添加恰当辅助线构造全等三角形是解答该题的关键.
同课章节目录
