北京版七年级数学下册《9.5 平均数第一课时》教学设计
文档属性
| 名称 | 北京版七年级数学下册《9.5 平均数第一课时》教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 49.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 20:13:55 | ||
图片预览



文档简介
《平均数第一课时》教学设计
一、教材分析:
教科书设计了以招聘英文翻译为背景的实际问题,根据不同的招聘要求,各项成绩的“重要程度”不同,从而平均成绩不同,由此引入加权平均数的概念。权的重要性在于它能够反映数据的相对“重要程度”。为了更好地说明这一点,教科书设计了“思考”栏目和例1,从不同方面体现权的作用,使学生更好地理解加权平均数,体会权的意义和作用。另外,本节课是本章的第一节课,所以还应注意对章前页的学习。
二、学情分析:
学生在小学已学过平均数,初步了解了平均数的实际意义,这个课时将在此基础上,在研究数据集中趋势的大背景下,学习加权平均数,体会权的意义、作用,并进一步体会平均数是刻画一组数据集中趋势的重要的统计量,是一组数据的“重心”。
三、教学目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
四、教学重点、难点:
教学重点:对权及加权平均数统计意义的理解。
教学难点:对权的意义的理解,用加权平均数分析一组数据的集中趋势。
五、教学问题诊断分析
加权平均数不同于简单的算术平均数,简单的算术平均数只与数据的大小有关,而加权平均数则还与该组数据的权相关,学生对权的意义和作用的理解会有困难,往往造成数据与权混淆不清,只会利用公式,而不知加权平均数的统计意义。
六、教学过程设计
活动一:创设情境,引入新知
结合我国的大背景——脱贫攻坚相关政策,让学生说一说他们所享受的相关政策,感受国家带给我们的民族自信,同时指出很多社会人士为了回报社会,自发的成立基金会支助贫困孩子读书,让学生知道感恩社会,感恩别人,学会感恩。同时,提出“支助对象如何选择”的问题,这就与以前所学的知识结合起来,达到了章引言的设计目的。
师生活动:利用以往所学的知识设计“如何确定资助对象”的活动流程。
师生讨论后的共同方案:
活动目的:确定资助对象。
1、对困难学生的实际情况进行走访调查。
2、收集、整理、描述相关数据。主要对学习成绩、德育表现、家庭困难程度进行打分,每项满分100分。
3、进行数据分析。
4、确定最终资助对象。
在进行数据分析时,运用小学时我们学均数,知道它可以反映一组数据的平均水平,导入新课。本节我们将在实际问题情境中,进一步探讨平均数的统计意义,了解它们在数据分析中的作用。
设计意图:完成章引言的设计目的。让学生回顾统计调查的一般步骤,了解本节的大致内容,体会数据分析是统计的重要环节,而平均数等统计量在数据分析中起着重要作用。
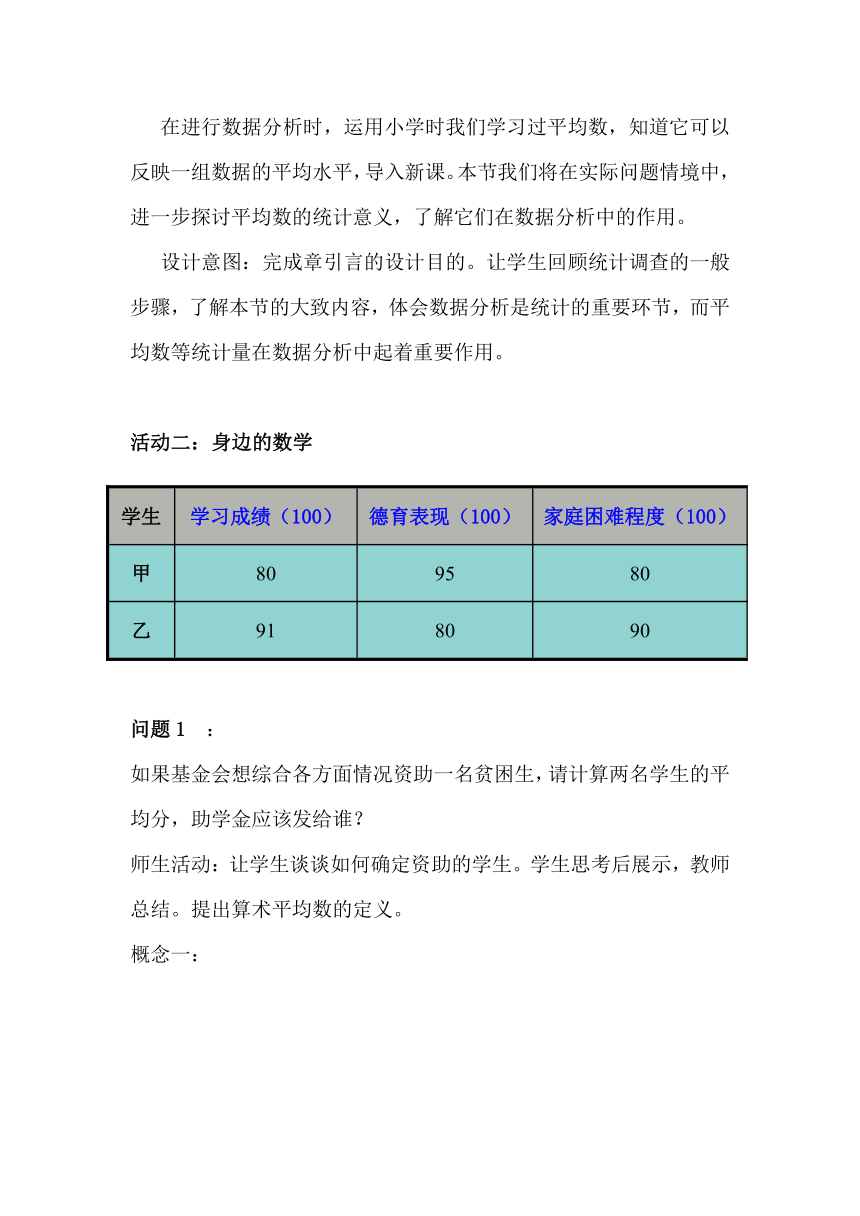
活动二:身边的数学
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题1 :
如果基金会想综合各方面情况资助一名贫困生,请计算两名学生的平均分,助学金应该发给谁?
师生活动:让学生谈谈如何确定资助的学生。学生思考后展示,教师总结。提出算术平均数的定义。
概念一:
活动二:问题深化,形成概念
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题2 如果基金会比较看重资助对象的德育表现,用算术平均数来衡量他们,合理吗?
师生活动:学生可以独立思考也可以相互讨论,
设计意图:用问题引起学生对将要学习的知识与以往知识形成碰撞,激发学生的思维和好奇心。
教师引导:
追问1:用小学学过的平均数解决问题2合理吗?为什么?
追问2:如何在计算平均数时体现各方面的差别?(学习成绩、德育表现、家庭困难程度按照3:5:2的比确定。)
师生活动:教师适时地追问,学生自主设计计算平均数的方法,教师收集整理学生的计算方法,并统一计算形式,讲解权的意义及加权平均数。
学生解答后展示。教师补全解答过程,规范解题格式。
设计意图:追问1让学生理解问题2与问题1的有区别,问题2中的每个数据的“重要程度”不同,追问2让学生自主探究如何在计算平均数时体现的每个数据的“重要程度”不同,从而体会权的意义。
形成概念:在问题2中,各个数据的重要程度不同(权不同),这种计算平均数的方法能否推广到一般?
追问:若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,这n个数据的平均数该如何计算?
师生活动:教师引导学生得到加权平均数公式
概念二:一般地,若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,则这n个数的加权平均数是。
设计意图:从特殊到一般,得到加权平均数的公式。
权的意义:(1)数据的重要程度(2)权衡轻重或份量大小
活动三:指导应用,强化新知
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题3 如果基金会既很看重德育表现又很看重学习成绩,请你选择一个合适的比,确定出资助对象。
师生活动:学生思考权的确定,各抒己见。只要思路是正确的,就给予肯定,最后选出一个比作为代表进行计算。学生完成,然后在黑板上板演,师生共同评价,主要格式。
设计目的:通过让学生自己确定权,让学生体会权的重要程度,体会权的作用。
活动四:理解新知
思考
1、前面三个小题的结果是否一样?为什么?比较问题(1)、(2)、(3),你能体会到权的作用吗?
2、算术平均数和加权平均数有什么区别和联系?
师生活动:学生思考、讨论,解决问题,最后师生共同总结。
(1)算术平均数是加权平均数的一种特殊情况。
(它特殊在各项的权相等)
(2)实际问题中,
各项权不等时,计算平均数时就采用加权平均数;
各项权相等时,可采用算术平均数。
设计意图:同一个问题背景,改变数据的权,则得到不同的结果,从而进一步体会权的意义与作用。理解简单的算术平均数与加权平均数之间的联系。
活动五:应用新知
例 一次演讲比赛中,评委按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).试比较谁的成绩更好.
活动六:练习扩展
某校八年级一次数学考试中,1班的平均分是90分,2班的平均分是95分,你能求出这两个班的数学平均分吗?
师生活动:学生完成问题,师生总结:
权的三种表达形式:比例、百分比、频数
活动七:课堂小结
结合以下问题,教师与学生一起回顾本节课所学主要内容。
(1)如何计算加权平均数?加权平均数在数据分析中的作用是什么?
(2)权的作用是什么?
设计意图:问题1引导学生回顾加权平均数的算法及意义,问题2引导学生回顾权的作用及意义。
七、布置作业
作业:
必做题:教科书第113页练习第2题;
选做题:教科书第121页习题20.1第1题.
请你设计一种求本班同学平均年龄的方案。
八、板书设计:
1、算术平均数:
2、“权”的意义:各个数据的“重要程度”.
3、加权平均数:
一般地,若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,则这n个数的加权平均数是。
4、加权平均数中的“权”的三种表现形式: (1)频数 (2)百分比 (3)比例
九、教学反思:
这节课,大部分学生表现积极,兴趣高。尤其在引入和后面解决几个问题时和总结权的几种形式时,学生们是争先恐后回答,并且会有自己的思考,有的同学还能把不同意见发表出来,师生在课堂上的交流活跃,在这种前提下,简便算法的推出就水到渠成了。
教学设计也努力体现新课改的新理念,把课堂交给了学生。充分注意培养学生数学的思维能力,教会学生从生活中学习数学,课内外结合等等。但有的学生基础并不好,上课时不能主动参与学习活动,被动地学习,收效一定不高。在加权平均数的定义讲解上,定义讲解怕基础不好的学生并不能完全接受。新课改提出教学要面向全体,在让每个学生在数学上都能得到不同程度的发展,可如果课堂学习我们只顾少数基础好的同学,那就与新课改理念相背了。所以,全面提高课堂教学质量方面,我们还有许多的问题需要探索。
一、教材分析:
教科书设计了以招聘英文翻译为背景的实际问题,根据不同的招聘要求,各项成绩的“重要程度”不同,从而平均成绩不同,由此引入加权平均数的概念。权的重要性在于它能够反映数据的相对“重要程度”。为了更好地说明这一点,教科书设计了“思考”栏目和例1,从不同方面体现权的作用,使学生更好地理解加权平均数,体会权的意义和作用。另外,本节课是本章的第一节课,所以还应注意对章前页的学习。
二、学情分析:
学生在小学已学过平均数,初步了解了平均数的实际意义,这个课时将在此基础上,在研究数据集中趋势的大背景下,学习加权平均数,体会权的意义、作用,并进一步体会平均数是刻画一组数据集中趋势的重要的统计量,是一组数据的“重心”。
三、教学目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
四、教学重点、难点:
教学重点:对权及加权平均数统计意义的理解。
教学难点:对权的意义的理解,用加权平均数分析一组数据的集中趋势。
五、教学问题诊断分析
加权平均数不同于简单的算术平均数,简单的算术平均数只与数据的大小有关,而加权平均数则还与该组数据的权相关,学生对权的意义和作用的理解会有困难,往往造成数据与权混淆不清,只会利用公式,而不知加权平均数的统计意义。
六、教学过程设计
活动一:创设情境,引入新知
结合我国的大背景——脱贫攻坚相关政策,让学生说一说他们所享受的相关政策,感受国家带给我们的民族自信,同时指出很多社会人士为了回报社会,自发的成立基金会支助贫困孩子读书,让学生知道感恩社会,感恩别人,学会感恩。同时,提出“支助对象如何选择”的问题,这就与以前所学的知识结合起来,达到了章引言的设计目的。
师生活动:利用以往所学的知识设计“如何确定资助对象”的活动流程。
师生讨论后的共同方案:
活动目的:确定资助对象。
1、对困难学生的实际情况进行走访调查。
2、收集、整理、描述相关数据。主要对学习成绩、德育表现、家庭困难程度进行打分,每项满分100分。
3、进行数据分析。
4、确定最终资助对象。
在进行数据分析时,运用小学时我们学均数,知道它可以反映一组数据的平均水平,导入新课。本节我们将在实际问题情境中,进一步探讨平均数的统计意义,了解它们在数据分析中的作用。
设计意图:完成章引言的设计目的。让学生回顾统计调查的一般步骤,了解本节的大致内容,体会数据分析是统计的重要环节,而平均数等统计量在数据分析中起着重要作用。
活动二:身边的数学
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题1 :
如果基金会想综合各方面情况资助一名贫困生,请计算两名学生的平均分,助学金应该发给谁?
师生活动:让学生谈谈如何确定资助的学生。学生思考后展示,教师总结。提出算术平均数的定义。
概念一:
活动二:问题深化,形成概念
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题2 如果基金会比较看重资助对象的德育表现,用算术平均数来衡量他们,合理吗?
师生活动:学生可以独立思考也可以相互讨论,
设计意图:用问题引起学生对将要学习的知识与以往知识形成碰撞,激发学生的思维和好奇心。
教师引导:
追问1:用小学学过的平均数解决问题2合理吗?为什么?
追问2:如何在计算平均数时体现各方面的差别?(学习成绩、德育表现、家庭困难程度按照3:5:2的比确定。)
师生活动:教师适时地追问,学生自主设计计算平均数的方法,教师收集整理学生的计算方法,并统一计算形式,讲解权的意义及加权平均数。
学生解答后展示。教师补全解答过程,规范解题格式。
设计意图:追问1让学生理解问题2与问题1的有区别,问题2中的每个数据的“重要程度”不同,追问2让学生自主探究如何在计算平均数时体现的每个数据的“重要程度”不同,从而体会权的意义。
形成概念:在问题2中,各个数据的重要程度不同(权不同),这种计算平均数的方法能否推广到一般?
追问:若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,这n个数据的平均数该如何计算?
师生活动:教师引导学生得到加权平均数公式
概念二:一般地,若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,则这n个数的加权平均数是。
设计意图:从特殊到一般,得到加权平均数的公式。
权的意义:(1)数据的重要程度(2)权衡轻重或份量大小
活动三:指导应用,强化新知
学生 学习成绩(100) 德育表现(100) 家庭困难程度(100)
甲 80 95 80
乙 91 80 90
问题3 如果基金会既很看重德育表现又很看重学习成绩,请你选择一个合适的比,确定出资助对象。
师生活动:学生思考权的确定,各抒己见。只要思路是正确的,就给予肯定,最后选出一个比作为代表进行计算。学生完成,然后在黑板上板演,师生共同评价,主要格式。
设计目的:通过让学生自己确定权,让学生体会权的重要程度,体会权的作用。
活动四:理解新知
思考
1、前面三个小题的结果是否一样?为什么?比较问题(1)、(2)、(3),你能体会到权的作用吗?
2、算术平均数和加权平均数有什么区别和联系?
师生活动:学生思考、讨论,解决问题,最后师生共同总结。
(1)算术平均数是加权平均数的一种特殊情况。
(它特殊在各项的权相等)
(2)实际问题中,
各项权不等时,计算平均数时就采用加权平均数;
各项权相等时,可采用算术平均数。
设计意图:同一个问题背景,改变数据的权,则得到不同的结果,从而进一步体会权的意义与作用。理解简单的算术平均数与加权平均数之间的联系。
活动五:应用新知
例 一次演讲比赛中,评委按演讲内容占50%、演讲能力占40%、演讲效果占10%的比例,计算选手的综合成绩(百分制).试比较谁的成绩更好.
活动六:练习扩展
某校八年级一次数学考试中,1班的平均分是90分,2班的平均分是95分,你能求出这两个班的数学平均分吗?
师生活动:学生完成问题,师生总结:
权的三种表达形式:比例、百分比、频数
活动七:课堂小结
结合以下问题,教师与学生一起回顾本节课所学主要内容。
(1)如何计算加权平均数?加权平均数在数据分析中的作用是什么?
(2)权的作用是什么?
设计意图:问题1引导学生回顾加权平均数的算法及意义,问题2引导学生回顾权的作用及意义。
七、布置作业
作业:
必做题:教科书第113页练习第2题;
选做题:教科书第121页习题20.1第1题.
请你设计一种求本班同学平均年龄的方案。
八、板书设计:
1、算术平均数:
2、“权”的意义:各个数据的“重要程度”.
3、加权平均数:
一般地,若n个数据x1,x2,…,xn的权分别为w1,w2,…,wn,则这n个数的加权平均数是。
4、加权平均数中的“权”的三种表现形式: (1)频数 (2)百分比 (3)比例
九、教学反思:
这节课,大部分学生表现积极,兴趣高。尤其在引入和后面解决几个问题时和总结权的几种形式时,学生们是争先恐后回答,并且会有自己的思考,有的同学还能把不同意见发表出来,师生在课堂上的交流活跃,在这种前提下,简便算法的推出就水到渠成了。
教学设计也努力体现新课改的新理念,把课堂交给了学生。充分注意培养学生数学的思维能力,教会学生从生活中学习数学,课内外结合等等。但有的学生基础并不好,上课时不能主动参与学习活动,被动地学习,收效一定不高。在加权平均数的定义讲解上,定义讲解怕基础不好的学生并不能完全接受。新课改提出教学要面向全体,在让每个学生在数学上都能得到不同程度的发展,可如果课堂学习我们只顾少数基础好的同学,那就与新课改理念相背了。所以,全面提高课堂教学质量方面,我们还有许多的问题需要探索。
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
