北京版八年级数学下册第十四章《一次函数》复习课教学设计
文档属性
| 名称 | 北京版八年级数学下册第十四章《一次函数》复习课教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 20:34:08 | ||
图片预览

文档简介
《一次函数》复习课教学设计
教学目标
1.梳理本章知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
教学重难点
对综合性题目,会合理使用数学思想方法探究解决
教学过程
知识构架
变化的世界建立数学模型
函数
一次函数的一般式 图像和性质
一次函数与一元一次方程
一元一次不等式
二元一次方程组
一次函数的应用
知识点
一.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
二.函数的三种表示法与特点
图象法
列表法
解析法
s=60t;S= πR2
1.思考:下面2个图形中,哪个图象是y关于x 的函数.
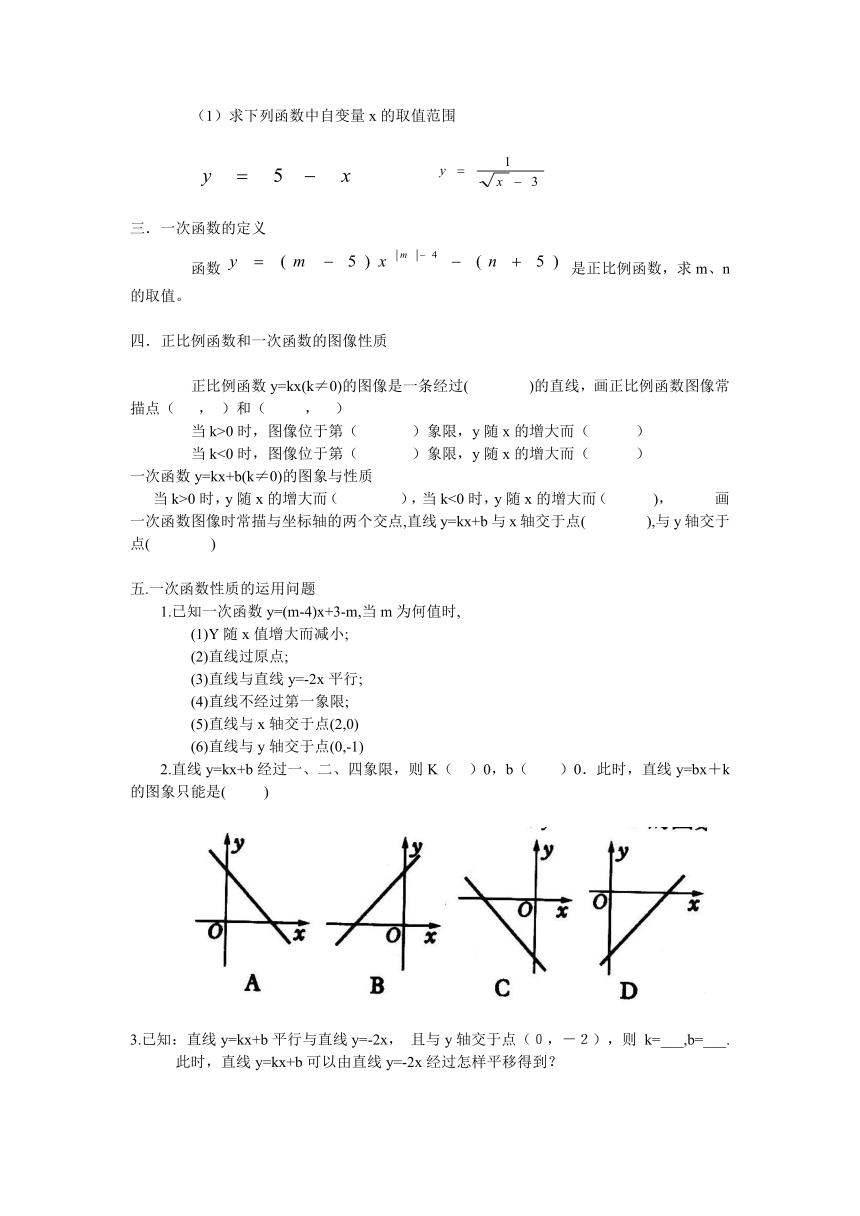
(1)求下列函数中自变量x的取值范围
三.一次函数的定义
函数是正比例函数,求m、n的取值。
四.正比例函数和一次函数的图像性质
正比例函数y=kx(k≠0)的图像是一条经过( )的直线,画正比例函数图像常描点( , )和( , )
当k>0时,图像位于第( )象限,y随x的增大而( )
当k<0时,图像位于第( )象限,y随x的增大而( )
一次函数y=kx+b(k≠0)的图象与性质
当k>0时,y随x的增大而( ),当k<0时,y随x的增大而( ), 画一次函数图像时常描与坐标轴的两个交点,直线y=kx+b与x轴交于点( ),与y轴交于点( )
五.一次函数性质的运用问题
1.已知一次函数y=(m-4)x+3-m,当m为何值时,
(1)Y随x值增大而减小;
(2)直线过原点;
(3)直线与直线y=-2x平行;
(4)直线不经过第一象限;
(5)直线与x轴交于点(2,0)
(6)直线与y轴交于点(0,-1)
2.直线y=kx+b经过一、二、四象限,则K( )0,b( )0.此时,直线y=bx+k的图象只能是( )
3.已知:直线y=kx+b平行与直线y=-2x, 且与y轴交于点(0,-2),则 k=___,b=___.
此时,直线y=kx+b可以由直线y=-2x经过怎样平移得到?
4. 一次函数的图象经过点(-2,-5),且与正比例函数的图象交于点Q(2,a)
(1) 求a的值;
(2) (2)求一次函数的解析式;
(3)当x为何值时,一次函数的函数值大于正比例函数的函数值?
六.一次函数与方程,不等式的关系
1.直线y=x+3与x轴的交点坐标为( ),所以相应的方程x+3=0的解是( ) .
2.设m,n为常数且m≠0,直线y=mx+n(如图所示), 则方程mx+n=0的解是 ________方程mx+n=-0.5的解是_______
-2
3.根据一次函数y=4x+4的图象:回答下列问题:
(1)x为何值时,y=0
(2)x为何值时,y>0
(3) x为何值时,y<0
(4)若0≤y≤4,求x的取值范围
七.应用与拓展
4. 为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(分钟)与通话费y元的关系如图所示:问题:1.通话多少分钟两种卡花费一样? 2.通话多少分钟便民卡优惠?3.通话多少分钟如意卡优惠?
如意卡优惠?
8. 深化拓展
已知:一次函数y=kx+b(k≠0)的图像与坐标轴围成的三角形的面积为9,又知方程kx+b=0的解为x=6,则所求一次函数的解析式为什么?
-2
-
o
x
y
4
-1
y=4x+4
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
教学目标
1.梳理本章知识脉络,加强知识点的巩固和理解.
2.进一步学会函数的研究方法,提高解题的灵活性.
3.对综合性题目,会合理使用数学思想方法探究解决.
教学重难点
对综合性题目,会合理使用数学思想方法探究解决
教学过程
知识构架
变化的世界建立数学模型
函数
一次函数的一般式 图像和性质
一次函数与一元一次方程
一元一次不等式
二元一次方程组
一次函数的应用
知识点
一.函数的概念:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯 一确定的值与其对应,那么我们就说x是自变量 ,y是x的函数。
二.函数的三种表示法与特点
图象法
列表法
解析法
s=60t;S= πR2
1.思考:下面2个图形中,哪个图象是y关于x 的函数.
(1)求下列函数中自变量x的取值范围
三.一次函数的定义
函数是正比例函数,求m、n的取值。
四.正比例函数和一次函数的图像性质
正比例函数y=kx(k≠0)的图像是一条经过( )的直线,画正比例函数图像常描点( , )和( , )
当k>0时,图像位于第( )象限,y随x的增大而( )
当k<0时,图像位于第( )象限,y随x的增大而( )
一次函数y=kx+b(k≠0)的图象与性质
当k>0时,y随x的增大而( ),当k<0时,y随x的增大而( ), 画一次函数图像时常描与坐标轴的两个交点,直线y=kx+b与x轴交于点( ),与y轴交于点( )
五.一次函数性质的运用问题
1.已知一次函数y=(m-4)x+3-m,当m为何值时,
(1)Y随x值增大而减小;
(2)直线过原点;
(3)直线与直线y=-2x平行;
(4)直线不经过第一象限;
(5)直线与x轴交于点(2,0)
(6)直线与y轴交于点(0,-1)
2.直线y=kx+b经过一、二、四象限,则K( )0,b( )0.此时,直线y=bx+k的图象只能是( )
3.已知:直线y=kx+b平行与直线y=-2x, 且与y轴交于点(0,-2),则 k=___,b=___.
此时,直线y=kx+b可以由直线y=-2x经过怎样平移得到?
4. 一次函数的图象经过点(-2,-5),且与正比例函数的图象交于点Q(2,a)
(1) 求a的值;
(2) (2)求一次函数的解析式;
(3)当x为何值时,一次函数的函数值大于正比例函数的函数值?
六.一次函数与方程,不等式的关系
1.直线y=x+3与x轴的交点坐标为( ),所以相应的方程x+3=0的解是( ) .
2.设m,n为常数且m≠0,直线y=mx+n(如图所示), 则方程mx+n=0的解是 ________方程mx+n=-0.5的解是_______
-2
3.根据一次函数y=4x+4的图象:回答下列问题:
(1)x为何值时,y=0
(2)x为何值时,y>0
(3) x为何值时,y<0
(4)若0≤y≤4,求x的取值范围
七.应用与拓展
4. 为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(分钟)与通话费y元的关系如图所示:问题:1.通话多少分钟两种卡花费一样? 2.通话多少分钟便民卡优惠?3.通话多少分钟如意卡优惠?
如意卡优惠?
8. 深化拓展
已知:一次函数y=kx+b(k≠0)的图像与坐标轴围成的三角形的面积为9,又知方程kx+b=0的解为x=6,则所求一次函数的解析式为什么?
-2
-
o
x
y
4
-1
y=4x+4
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
同课章节目录
