北京版八年级数学下册《15.5 三角形中位线定理》教学设计
文档属性
| 名称 | 北京版八年级数学下册《15.5 三角形中位线定理》教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 193.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-21 20:35:43 | ||
图片预览

文档简介
15.5.三角形中位线定理(1)
教学目标:
1.理解三角形中位线定义,探索并证明三角形中位线定理,会应用定理进行简单的计算和证明;
2.通过画图、测量、猜想、验证与证明等活动,积累数学活动经验,发展推理论证的能力;通过运用四边形的相关知识证明了三角形的中位线定理,体会知识间的相互联系与转化;
3.通过同伴间的合作与交流,体会成功的快乐,感受数学结论的严谨性,体验数学活动充满探索与创造.
教学重点:三角形中位线定理的证明和简单应用.
教学难点:三角形中位线定理证明思路的探究.
教学方法:教师启发讲授与学生自主探究相结合.
【引入课题】
利用实际问题引入课题.
【设计意图】创设情境,激发学生的学习兴趣.
【探究新知】
1.三角形的中位线定义.
连接三角形两边中点的线段,叫做三角形的中位线.
如图,在中,分别是的中点,则线段是的_______,线段是的_______,线段是的_______.
三角形有几条中位线 三角形的中位线与中线有什么区别
①三角形的中位线与中线都是三角形中的重要线段,一个三角形有三条中位线,三条中线.
②三角形的中位线的两端点都是三角形边的中点,而三角形的中线只有一个端点是边的中点,另一个端点是三角形的一个顶点.
③三角形有三条中线,它们相交于一点,三角形有三条中位线,它们组成一个三角形.
【设计意图】通过与三角形中线概念的对比,进一步明确中位线的概念.
2.探究三角形中位线的性质.
画一画,量一量,猜一猜:
⑴任意画一个,分别取的中点,连接,思考:三角形的中位线与第三边有什么关系
⑵观察,测量,得到猜想:三角形的中位线平行于第三边且等于第三边的一半.().
⑶用几何画板验证猜想.
【设计意图】学生先自主探索,初步得出结论,然后师生再一起交流所得的结论.
性质的证明:
⑴分析命题,探究证明思路:
引导学生写出已知和求证,在学生独立思考的基础上,引导学生思考猜想中的两个结论:平行关系和线段的倍分关系,可以联想我们之前学过的平行四边形的知识来解决,鼓励学生尝试证明.
⑵在学生独立思考的基础上,交流证明方法,理清思路.
⑶小组代表汇报,交流证明方法.
⑷引导学生进行反思,不同添加辅助线的方法,引出不同的证法,但都是将问题转化到平行四边形中解决.提倡选择一种比较简洁的方法进行证明.
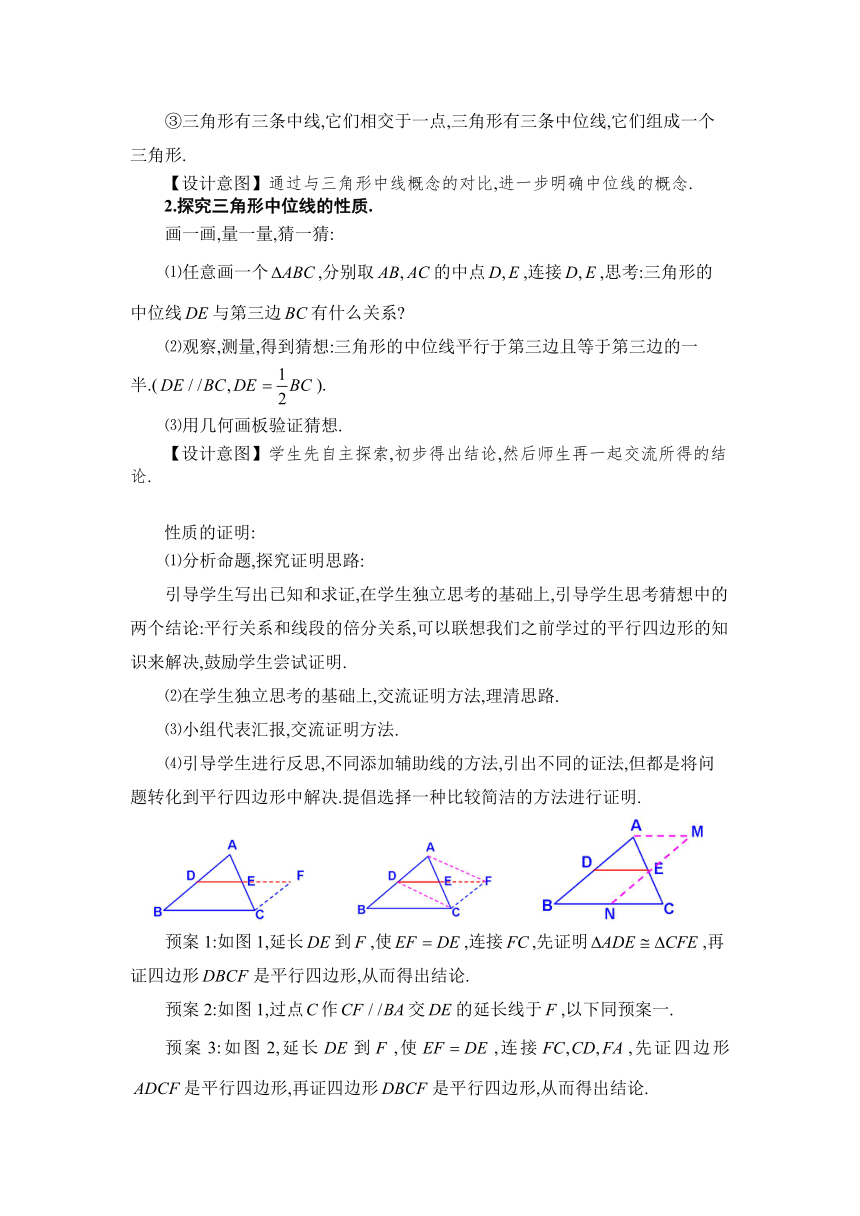
预案1:如图1,延长到,使,连接,先证明,再证四边形是平行四边形,从而得出结论.
预案2:如图1,过点作交的延长线于,以下同预案一.
预案3:如图2,延长到,使,连接,先证四边形是平行四边形,再证四边形是平行四边形,从而得出结论.
预案4:如图3,过点作的平行线交于,过点作的平行线交的延长线于,先证四边形是平行四边形,且,再证四边形是平行四边形,从而得出结论.
【设计意图】三角形中位线定理的证明这本节课的难点,这里我通过证明之前的思路提示、学生先独立思考,然后再组内交流不同的思路来突破这一难点.通过定理的证明,培养学生的识图能力与推理能力.另外,证明思路的拓展和提高,我准备了其它的证明,并适时进行点拨和小结.
⑸得出三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半.
符号语言:∵中,分别是的中点,
∴.
⑹三角形中位线定理的作用是什么 (可以用来证明线段间的位置关系和数量关系.)
【设计意图】通过运用平行四边形的相关知识,证明了三角形中的一个重要定理.在这一过程中,学生体会知识间的相互联系与转化.
【应用新知】
【例1】在中,分别是边的中点.
①若,则 度;
②若,则 ;
③若,则 .
【设计意图】运用新知,解决简单的问题.
【例2】如图,在中,.
求证:互相平分.
思路分析:欲证互相平分,
只需证明四边形是平行四边形即可,
因此需要作辅助线:连接,
于是在图中出现了三角形的中位线,利用三角形的中位线定理,可以证明四边形是平行四边形.
【思考】如图,顺次连接三角形三边的中点,把大三角形分成四个小三角形,这四个小三角形有什么关系
围绕上图,设置问题:
在中,分别是的中点.
1.图中有 组平行线,有 个平行四边形.
2.与的周长之比为 ,面积之比为 .
【设计意图】问题回解,提高解决问题的能力与意识.
【总结提升】
1.基础知识:
⑴三角线的中位线定义以及它与三角形中线的区别;
⑵三角线中位线的性质及其应用.
2.基本技能:
三角形中位线定理是三角形的一个重要性质定理,它的特点是:在同一个题设下,有两个结论,一个结论是表明位置关系的,另一个结论是表明数量关系的,在应用这个定理时,不一定同时需要两个结论,有时需要平行关系,有时需要倍分关系,可以根据具体情况,按需选用.
⑴在三角形中给出一边中点时,可以考虑利用另一边的中点,作出中位线;
⑵线段的倍分可以转化为相等问题来解决;
⑶三角形的中位线定理的发现过程所用到的数学方法(包括画图、测量、猜想、验证、归纳、证明等).
3.基本思想方法:
⑴“转化”思想(利用三角形的知识研究了四边形的知识,反过来也可以利用四边形的相关知识研究三角形的重要性质,体现了事物间的相互转化与相互联系);
⑵从“特殊到一般”的研究问题的思路.
教学目标:
1.理解三角形中位线定义,探索并证明三角形中位线定理,会应用定理进行简单的计算和证明;
2.通过画图、测量、猜想、验证与证明等活动,积累数学活动经验,发展推理论证的能力;通过运用四边形的相关知识证明了三角形的中位线定理,体会知识间的相互联系与转化;
3.通过同伴间的合作与交流,体会成功的快乐,感受数学结论的严谨性,体验数学活动充满探索与创造.
教学重点:三角形中位线定理的证明和简单应用.
教学难点:三角形中位线定理证明思路的探究.
教学方法:教师启发讲授与学生自主探究相结合.
【引入课题】
利用实际问题引入课题.
【设计意图】创设情境,激发学生的学习兴趣.
【探究新知】
1.三角形的中位线定义.
连接三角形两边中点的线段,叫做三角形的中位线.
如图,在中,分别是的中点,则线段是的_______,线段是的_______,线段是的_______.
三角形有几条中位线 三角形的中位线与中线有什么区别
①三角形的中位线与中线都是三角形中的重要线段,一个三角形有三条中位线,三条中线.
②三角形的中位线的两端点都是三角形边的中点,而三角形的中线只有一个端点是边的中点,另一个端点是三角形的一个顶点.
③三角形有三条中线,它们相交于一点,三角形有三条中位线,它们组成一个三角形.
【设计意图】通过与三角形中线概念的对比,进一步明确中位线的概念.
2.探究三角形中位线的性质.
画一画,量一量,猜一猜:
⑴任意画一个,分别取的中点,连接,思考:三角形的中位线与第三边有什么关系
⑵观察,测量,得到猜想:三角形的中位线平行于第三边且等于第三边的一半.().
⑶用几何画板验证猜想.
【设计意图】学生先自主探索,初步得出结论,然后师生再一起交流所得的结论.
性质的证明:
⑴分析命题,探究证明思路:
引导学生写出已知和求证,在学生独立思考的基础上,引导学生思考猜想中的两个结论:平行关系和线段的倍分关系,可以联想我们之前学过的平行四边形的知识来解决,鼓励学生尝试证明.
⑵在学生独立思考的基础上,交流证明方法,理清思路.
⑶小组代表汇报,交流证明方法.
⑷引导学生进行反思,不同添加辅助线的方法,引出不同的证法,但都是将问题转化到平行四边形中解决.提倡选择一种比较简洁的方法进行证明.
预案1:如图1,延长到,使,连接,先证明,再证四边形是平行四边形,从而得出结论.
预案2:如图1,过点作交的延长线于,以下同预案一.
预案3:如图2,延长到,使,连接,先证四边形是平行四边形,再证四边形是平行四边形,从而得出结论.
预案4:如图3,过点作的平行线交于,过点作的平行线交的延长线于,先证四边形是平行四边形,且,再证四边形是平行四边形,从而得出结论.
【设计意图】三角形中位线定理的证明这本节课的难点,这里我通过证明之前的思路提示、学生先独立思考,然后再组内交流不同的思路来突破这一难点.通过定理的证明,培养学生的识图能力与推理能力.另外,证明思路的拓展和提高,我准备了其它的证明,并适时进行点拨和小结.
⑸得出三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半.
符号语言:∵中,分别是的中点,
∴.
⑹三角形中位线定理的作用是什么 (可以用来证明线段间的位置关系和数量关系.)
【设计意图】通过运用平行四边形的相关知识,证明了三角形中的一个重要定理.在这一过程中,学生体会知识间的相互联系与转化.
【应用新知】
【例1】在中,分别是边的中点.
①若,则 度;
②若,则 ;
③若,则 .
【设计意图】运用新知,解决简单的问题.
【例2】如图,在中,.
求证:互相平分.
思路分析:欲证互相平分,
只需证明四边形是平行四边形即可,
因此需要作辅助线:连接,
于是在图中出现了三角形的中位线,利用三角形的中位线定理,可以证明四边形是平行四边形.
【思考】如图,顺次连接三角形三边的中点,把大三角形分成四个小三角形,这四个小三角形有什么关系
围绕上图,设置问题:
在中,分别是的中点.
1.图中有 组平行线,有 个平行四边形.
2.与的周长之比为 ,面积之比为 .
【设计意图】问题回解,提高解决问题的能力与意识.
【总结提升】
1.基础知识:
⑴三角线的中位线定义以及它与三角形中线的区别;
⑵三角线中位线的性质及其应用.
2.基本技能:
三角形中位线定理是三角形的一个重要性质定理,它的特点是:在同一个题设下,有两个结论,一个结论是表明位置关系的,另一个结论是表明数量关系的,在应用这个定理时,不一定同时需要两个结论,有时需要平行关系,有时需要倍分关系,可以根据具体情况,按需选用.
⑴在三角形中给出一边中点时,可以考虑利用另一边的中点,作出中位线;
⑵线段的倍分可以转化为相等问题来解决;
⑶三角形的中位线定理的发现过程所用到的数学方法(包括画图、测量、猜想、验证、归纳、证明等).
3.基本思想方法:
⑴“转化”思想(利用三角形的知识研究了四边形的知识,反过来也可以利用四边形的相关知识研究三角形的重要性质,体现了事物间的相互转化与相互联系);
⑵从“特殊到一般”的研究问题的思路.
同课章节目录
