10.1中心对称 课件
图片预览






文档简介
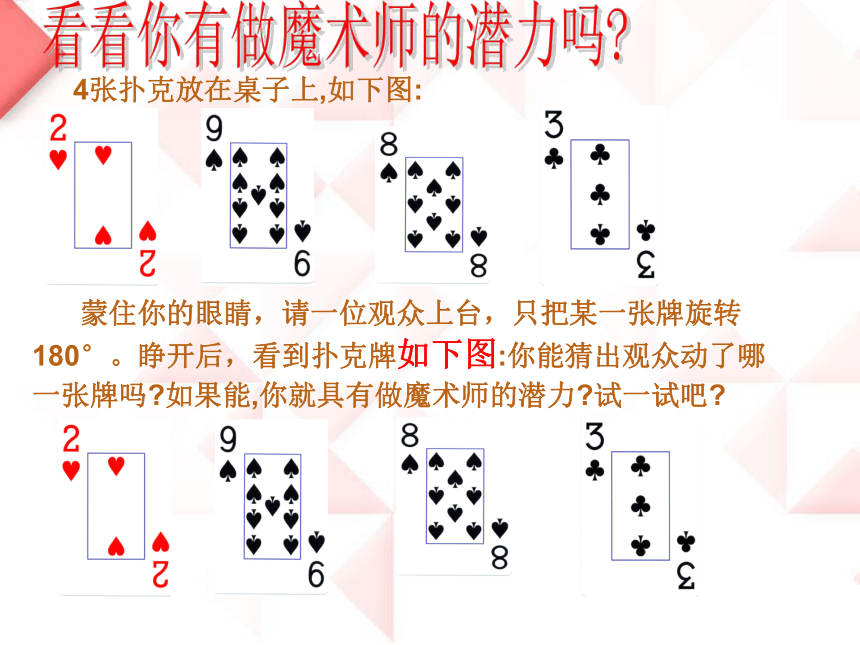
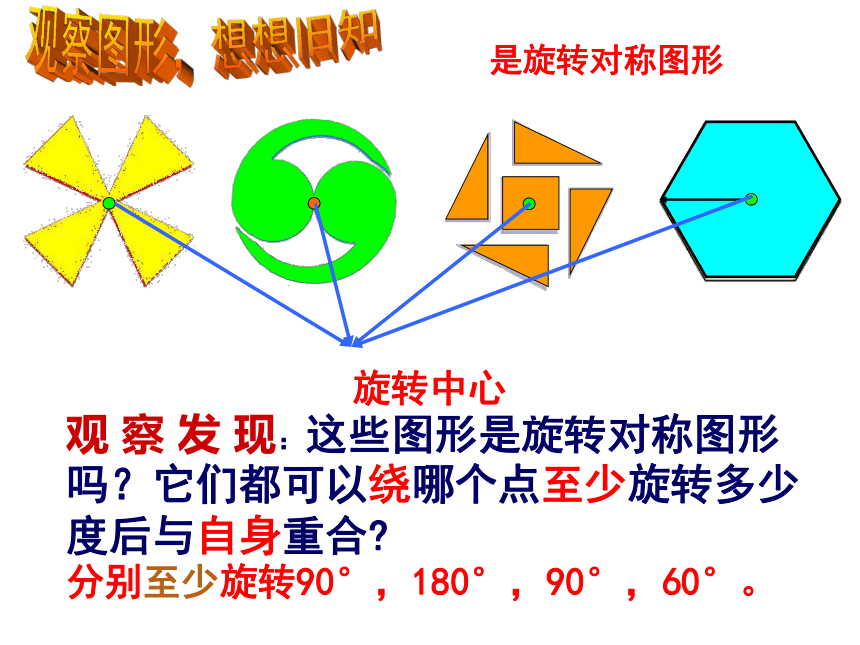
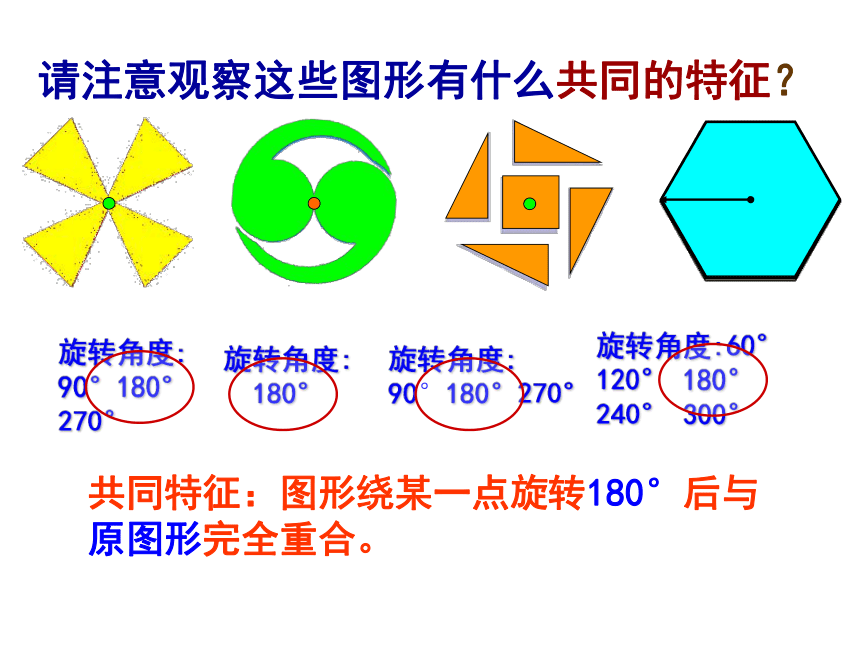
课件24张PPT。10.4.1中心对称七年级下册4张扑克放在桌子上,如下图: 蒙住你的眼睛,请一位观众上台,只把某一张牌旋转180°。睁开后,看到扑克牌如下图:你能猜出观众动了哪一张牌吗?如果能,你就具有做魔术师的潜力?试一试吧?看看你有做魔术师的潜力吗?观 察 发 现:这些图形是旋转对称图形吗?它们都可以绕哪个点至少旋转多少度后与自身重合? 观察图形,想想旧知是旋转对称图形分别至少旋转90°,180°,90°,60°。请注意观察这些图形有什么共同的特征?旋转角度:
90°180°
270°旋转角度:
180°旋转角度:
90°180°270°旋转角度:60°
120° 180°
240° 300°共同特征:图形绕某一点旋转180°后与原图形完全重合。 在平面内,一个图形绕某个点旋转180o,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形。中心对称图形的定义180o重合某个点中心对称图形是旋转对称图形吗?“旋转对称图形”与“中心对称图形”的关系: 旋转对称图形不一定是中心对称图形,中心对称图形一定是旋转对称图形。
若旋转对称图形是中心对称图形时,则旋转中心也叫做对称中心。你想知道我是怎样猜到的吗?游戏大解密生活中的数学留心生活,数学知识能为你增添许多乐趣!游戏大解密HI英文中的中心对称图形:NXOS中心对称图形的中文字:口日目回田Z中A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z 下面的英文字母中哪些是中心对称图形?学科中的数学A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z 下面哪些图形是中心对称图形?(4)正三角形(5)正五边形(6)正八边形方法点拨:只要将图形绕对称中心旋转180°,看能否与原图形重合。边数为偶数的正多边形都是中心对称图形。都是一个图形具有的特征有一个对称
中心——点有一条对称轴——直线图形绕中心旋转180度与自身重合图形沿轴翻折180度与自身重合请说出轴对称图形与中心对称图形的异同C中心对称图形上的每一对对应点所连成的线段都经过对称中心,并且被对称中心平分.探索中心对称图形的性质ABCDEFO 把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.观察: A、O、D三点的位置关系怎样?线段AO、DO的大小关系呢?两图成中心对称由旋转180°知道A、O、D三点在一直线上,B、O、E且OA=OD,同理 在一直线上,且 ,C、O、F在一直线上, 且OC=OF.OB=OE个图形中, 连结即:在成中心对称的两对称点的线段都经过对称中心, 并且被对称中心平分. 反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两
个图形看作一个整体,则成为中心对称图形。例 如图,已知△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称。解:A′C′B′∴△A′B′C′就是所要画的三角形。应 用 一如图,在矩形ABCD中,AD>AB,O 为对称中心,过O画 一直线分别交BC,AD于M、N。
探索:梯形ABMN的面积是否等于梯形CDNM的面积?应 用 二结论:在中心对称图形中,过对称中心的任意直线都会平分该图形的面积。练习:如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。动手活动:动手活动: 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。动手活动: 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。人们喜欢音乐,因为它有优美和谐的旋律;人们喜欢图画,因为它能描绘人和自然的美; 那么, 我们应该更喜欢数学,因为它像音乐一样的和谐,像画一样的优美。它在更深的层次上, 揭示自然界和人类社会内在的旋律。数学学习可以让我们发现美、认识美、创造美。发现美、认识美、创造美。 作业 课本:
第132页 第1,2,3,4题
90°180°
270°旋转角度:
180°旋转角度:
90°180°270°旋转角度:60°
120° 180°
240° 300°共同特征:图形绕某一点旋转180°后与原图形完全重合。 在平面内,一个图形绕某个点旋转180o,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形。中心对称图形的定义180o重合某个点中心对称图形是旋转对称图形吗?“旋转对称图形”与“中心对称图形”的关系: 旋转对称图形不一定是中心对称图形,中心对称图形一定是旋转对称图形。
若旋转对称图形是中心对称图形时,则旋转中心也叫做对称中心。你想知道我是怎样猜到的吗?游戏大解密生活中的数学留心生活,数学知识能为你增添许多乐趣!游戏大解密HI英文中的中心对称图形:NXOS中心对称图形的中文字:口日目回田Z中A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z 下面的英文字母中哪些是中心对称图形?学科中的数学A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z 下面哪些图形是中心对称图形?(4)正三角形(5)正五边形(6)正八边形方法点拨:只要将图形绕对称中心旋转180°,看能否与原图形重合。边数为偶数的正多边形都是中心对称图形。都是一个图形具有的特征有一个对称
中心——点有一条对称轴——直线图形绕中心旋转180度与自身重合图形沿轴翻折180度与自身重合请说出轴对称图形与中心对称图形的异同C中心对称图形上的每一对对应点所连成的线段都经过对称中心,并且被对称中心平分.探索中心对称图形的性质ABCDEFO 把一个图形绕着某一点旋转180度, 能和 另一个图形重合,那么,我们就说这两个图形成中心对称, 这个点就叫对称中心,这两个图形中的对应点, 叫做关于中心的对称点.观察: A、O、D三点的位置关系怎样?线段AO、DO的大小关系呢?两图成中心对称由旋转180°知道A、O、D三点在一直线上,B、O、E且OA=OD,同理 在一直线上,且 ,C、O、F在一直线上, 且OC=OF.OB=OE个图形中, 连结即:在成中心对称的两对称点的线段都经过对称中心, 并且被对称中心平分. 反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称。把一个图形绕着某一个点旋转180?,如果他能够与另一个图形重合,那么就说这两个图形成中心对称,两个图形关于点对称也称中心对称如果一个图形绕着一个点旋转180?后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形若把中心对称图形的两部分分别看作两个图形,则它们成中心对称,若把中心对称的两
个图形看作一个整体,则成为中心对称图形。例 如图,已知△ABC和点O,画△A′B′C′,使△A′B′C′和△ABC关于点O成中心对称。解:A′C′B′∴△A′B′C′就是所要画的三角形。应 用 一如图,在矩形ABCD中,AD>AB,O 为对称中心,过O画 一直线分别交BC,AD于M、N。
探索:梯形ABMN的面积是否等于梯形CDNM的面积?应 用 二结论:在中心对称图形中,过对称中心的任意直线都会平分该图形的面积。练习:如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。动手活动:动手活动: 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。动手活动: 如图,有一块“L”型土地,现要将土地平均分配给两户,请你画一条直线把图形分成面积相等的两个部分。用三种不同方式画出草图,并说明理由。人们喜欢音乐,因为它有优美和谐的旋律;人们喜欢图画,因为它能描绘人和自然的美; 那么, 我们应该更喜欢数学,因为它像音乐一样的和谐,像画一样的优美。它在更深的层次上, 揭示自然界和人类社会内在的旋律。数学学习可以让我们发现美、认识美、创造美。发现美、认识美、创造美。 作业 课本:
第132页 第1,2,3,4题
