八年级数学下册一次函数知识复习 教案
图片预览


文档简介
教学内容 一次函数的图像和性质用待定系数法求一次函数
教学目标 1、掌握一次函数的图像和性质2、掌握用待定系数法求一次函数解析式的方法
教学重点 一次函数的图像和性质
教学难点 灵活运用一次函数的图像和性质解决问题
教学过程
前课回顾
正比例函数,一次函数的概念
错题重现
1、已知y+5与3x+5成正比例,且当x=1时,y=3.
(1)求出y与x的函数关系式;
(2)作出该函数的图象;
(3)设点P(a,-2)在这条直线上,求P点的坐标;
(4)如果自变量x的取值范围是0≤x≤5,求y的取值范围.2、 已知一次函数y=(3-k)x-2k2+18.(1)k为何值时,它的图象经过原点?(2)k为何值时,它的图象经过点(0,-2) (3)k为何值时,它的图象平行于直线y=-x?(4)k为何值时,y随x的增大而减小?
知识详解
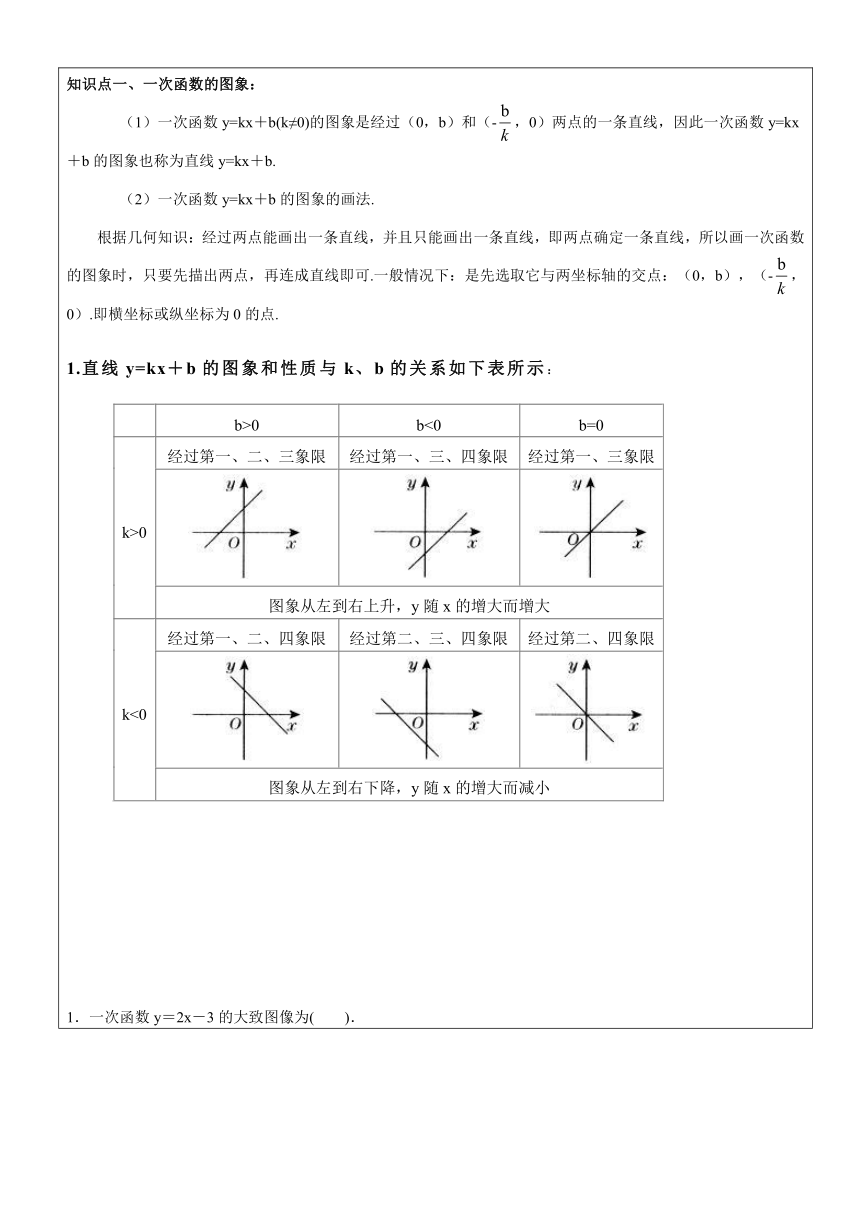
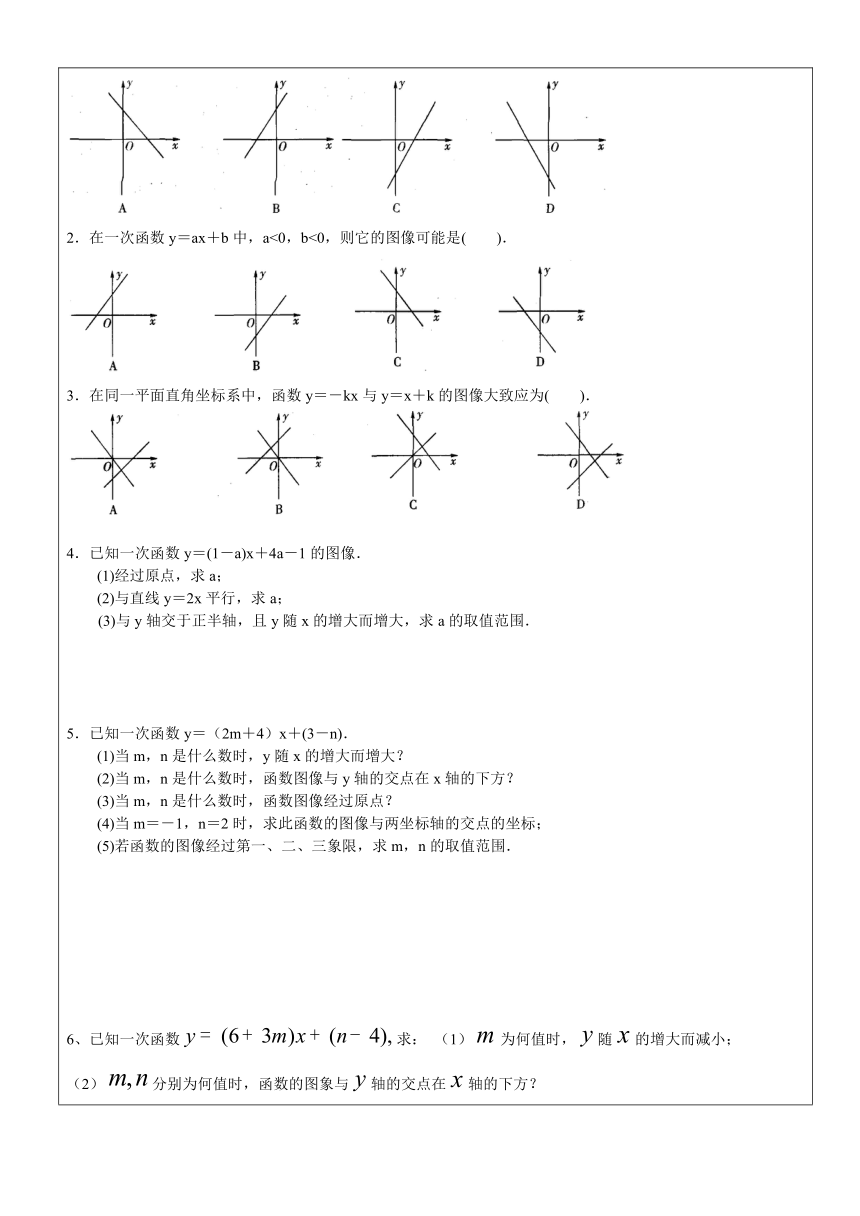
知识点一、一次函数的图象: (1)一次函数y=kx+b(k≠0)的图象是经过(0,b)和(-,0)两点的一条直线,因此一次函数y=kx+b的图象也称为直线y=kx+b. (2)一次函数y=kx+b的图象的画法. 根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b),(-,0).即横坐标或纵坐标为0的点.1.直线y=kx+b的图象和性质与k、b的关系如下表所示: b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y随x的增大而减小1.一次函数y=2x-3的大致图像为( ).2.在一次函数y=ax+b中,a<0,b<0,则它的图像可能是( ). 3.在同一平面直角坐标系中,函数y=-kx与y=x+k的图像大致应为( ). 4.已知一次函数y=(1-a)x+4a-1的图像. (1)经过原点,求a; (2)与直线y=2x平行,求a;(3)与y轴交于正半轴,且y随x的增大而增大,求a的取值范围.5.已知一次函数y=(2m+4)x+(3-n). (1)当m,n是什么数时,y随x的增大而增大? (2)当m,n是什么数时,函数图像与y轴的交点在x轴的下方? (3)当m,n是什么数时,函数图像经过原点? (4)当m=-1,n=2时,求此函数的图像与两坐标轴的交点的坐标;(5)若函数的图像经过第一、二、三象限,求m,n的取值范围.6、已知一次函数求: (1)为何值时,随的增大而减小; (2)分别为何值时,函数的图象与轴的交点在轴的下方?(3)分别为何值时,函数的图象经过原点?(4)当时,设此一次函数与轴交于A,与轴交于B,试求面积。知识点二、待定系数法求函数解析式:这样先设出函数解析式,再确定解析式中未知的系数,从而具体写出这个式子的方法 常用步骤方法: ①确定两点坐标 ②设一次函数为Y=kx+b ③把两点坐标代入得关于K,b方程组,求出K,b ④把K,b代入可得解析式1.已知直线y=kx+b经过点A(0,6),B(3,0). (1)求出这条直线的函数关系式; (2)若这条直线经过点P(m,2),求m的值;(3)求这条直线与两坐标轴所围成的三角形的面积.2. 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的解析式;(2)求△AOB的面积.知识点三、一次函数平移规律 (1).y=k(x-n)+b就是向右平移n个单位
(2).y=k(x+n)+b就是向左平移n个单位
口诀:右减左加
(3).y=kx+b+n就是向上平移n个单位
(4).y=kx+b-n就是向下平移n个单位
口诀:上加下减1.如图,一次函数y=kx+b的图像与正比例函数y=2x的图像平行且经过点A(1,-2),则kb=_______.2.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(a,b),且2a+b=6,则直线AB的解析式是( ). A.y=2x-3 B.y=-2x-6 C.y=-2x+3 D.y=-2x+6知识点四、一次函数与二元一次方程及一元一次不等式1.如图,已知函数y=x+b和y=ax+3的图像交点为P,则不等式x+b>ax+3的解集为_______. 2.根据国家发改委实施“阶梯电价”的有关文件要求,对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费122.5元,该市一户居民在5月以后,某月用电x千瓦时,当月交电费y元. (1)上表中,a=_______;b=_______; (2)请直接写出y与x之间的函数关系式;(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?
真题再现
1.如图,在平面直角坐标系xOy中,已知正比例函数与一次函数的图象交于点A.(1)求点A的坐标;(2)设x轴上有一点P(,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图象于点B、C,连接OC.若BC=OA,求△OBC的面积.2.已知直线经过点(-1,6)和(1,2),它和x轴、y轴分别交于B和A;直线经过点(2,-4)和(0,-3),它和x轴、y轴的交点分别是D和C。(1)求直线和的解析式;(2)求四边形ABCD的面积;(3)设直线与交于点P,求△PBC的面积。 3.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:(1)乙车的速度是 千米/时,t= 小时;(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;(3)直接写出乙车出发多长时间两车相距120千米.
变式训练
变式一、如图,已知函数的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P (其中>2),过点P作x轴的垂线,分别交函数和的图象于点C、D.(1)求点A的坐标;(2)若OB=CD,求的值.变式二、国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.(1)商店至多可以购买冰箱多少台?类别彩电冰箱洗衣机进价(元/台)200016001000售价(元/台)230018001100(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
课堂检测
1.正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A. B. C. D.2.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是……………………………………………………………( )A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+33.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到……………………………………………………( )A.M处; B.N处; C.P处; D.Q处;4.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D是OA的中的,点E在AB上,当△CDE的周长最小时,点E的坐标为A. B. C. D.
4
教学目标 1、掌握一次函数的图像和性质2、掌握用待定系数法求一次函数解析式的方法
教学重点 一次函数的图像和性质
教学难点 灵活运用一次函数的图像和性质解决问题
教学过程
前课回顾
正比例函数,一次函数的概念
错题重现
1、已知y+5与3x+5成正比例,且当x=1时,y=3.
(1)求出y与x的函数关系式;
(2)作出该函数的图象;
(3)设点P(a,-2)在这条直线上,求P点的坐标;
(4)如果自变量x的取值范围是0≤x≤5,求y的取值范围.2、 已知一次函数y=(3-k)x-2k2+18.(1)k为何值时,它的图象经过原点?(2)k为何值时,它的图象经过点(0,-2) (3)k为何值时,它的图象平行于直线y=-x?(4)k为何值时,y随x的增大而减小?
知识详解
知识点一、一次函数的图象: (1)一次函数y=kx+b(k≠0)的图象是经过(0,b)和(-,0)两点的一条直线,因此一次函数y=kx+b的图象也称为直线y=kx+b. (2)一次函数y=kx+b的图象的画法. 根据几何知识:经过两点能画出一条直线,并且只能画出一条直线,即两点确定一条直线,所以画一次函数的图象时,只要先描出两点,再连成直线即可.一般情况下:是先选取它与两坐标轴的交点:(0,b),(-,0).即横坐标或纵坐标为0的点.1.直线y=kx+b的图象和性质与k、b的关系如下表所示: b>0b<0b=0k>0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升,y随x的增大而增大k<0经过第一、二、四象限经过第二、三、四象限经过第二、四象限图象从左到右下降,y随x的增大而减小1.一次函数y=2x-3的大致图像为( ).2.在一次函数y=ax+b中,a<0,b<0,则它的图像可能是( ). 3.在同一平面直角坐标系中,函数y=-kx与y=x+k的图像大致应为( ). 4.已知一次函数y=(1-a)x+4a-1的图像. (1)经过原点,求a; (2)与直线y=2x平行,求a;(3)与y轴交于正半轴,且y随x的增大而增大,求a的取值范围.5.已知一次函数y=(2m+4)x+(3-n). (1)当m,n是什么数时,y随x的增大而增大? (2)当m,n是什么数时,函数图像与y轴的交点在x轴的下方? (3)当m,n是什么数时,函数图像经过原点? (4)当m=-1,n=2时,求此函数的图像与两坐标轴的交点的坐标;(5)若函数的图像经过第一、二、三象限,求m,n的取值范围.6、已知一次函数求: (1)为何值时,随的增大而减小; (2)分别为何值时,函数的图象与轴的交点在轴的下方?(3)分别为何值时,函数的图象经过原点?(4)当时,设此一次函数与轴交于A,与轴交于B,试求面积。知识点二、待定系数法求函数解析式:这样先设出函数解析式,再确定解析式中未知的系数,从而具体写出这个式子的方法 常用步骤方法: ①确定两点坐标 ②设一次函数为Y=kx+b ③把两点坐标代入得关于K,b方程组,求出K,b ④把K,b代入可得解析式1.已知直线y=kx+b经过点A(0,6),B(3,0). (1)求出这条直线的函数关系式; (2)若这条直线经过点P(m,2),求m的值;(3)求这条直线与两坐标轴所围成的三角形的面积.2. 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的解析式;(2)求△AOB的面积.知识点三、一次函数平移规律 (1).y=k(x-n)+b就是向右平移n个单位
(2).y=k(x+n)+b就是向左平移n个单位
口诀:右减左加
(3).y=kx+b+n就是向上平移n个单位
(4).y=kx+b-n就是向下平移n个单位
口诀:上加下减1.如图,一次函数y=kx+b的图像与正比例函数y=2x的图像平行且经过点A(1,-2),则kb=_______.2.如图,把直线y=-2x向上平移后得到直线AB,直线AB经过点(a,b),且2a+b=6,则直线AB的解析式是( ). A.y=2x-3 B.y=-2x-6 C.y=-2x+3 D.y=-2x+6知识点四、一次函数与二元一次方程及一元一次不等式1.如图,已知函数y=x+b和y=ax+3的图像交点为P,则不等式x+b>ax+3的解集为_______. 2.根据国家发改委实施“阶梯电价”的有关文件要求,对居民生活用电试行“阶梯电价”收费,具体收费标准见下表:5月份,该市居民甲用电100千瓦时,交电费60元;居民乙用电200千瓦时,交电费122.5元,该市一户居民在5月以后,某月用电x千瓦时,当月交电费y元. (1)上表中,a=_______;b=_______; (2)请直接写出y与x之间的函数关系式;(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?
真题再现
1.如图,在平面直角坐标系xOy中,已知正比例函数与一次函数的图象交于点A.(1)求点A的坐标;(2)设x轴上有一点P(,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交和的图象于点B、C,连接OC.若BC=OA,求△OBC的面积.2.已知直线经过点(-1,6)和(1,2),它和x轴、y轴分别交于B和A;直线经过点(2,-4)和(0,-3),它和x轴、y轴的交点分别是D和C。(1)求直线和的解析式;(2)求四边形ABCD的面积;(3)设直线与交于点P,求△PBC的面积。 3.甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:(1)乙车的速度是 千米/时,t= 小时;(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;(3)直接写出乙车出发多长时间两车相距120千米.
变式训练
变式一、如图,已知函数的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P (其中>2),过点P作x轴的垂线,分别交函数和的图象于点C、D.(1)求点A的坐标;(2)若OB=CD,求的值.变式二、国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.(1)商店至多可以购买冰箱多少台?类别彩电冰箱洗衣机进价(元/台)200016001000售价(元/台)230018001100(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
课堂检测
1.正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A. B. C. D.2.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是……………………………………………………………( )A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+33.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到……………………………………………………( )A.M处; B.N处; C.P处; D.Q处;4.矩形OABC在平面直角坐标系中的位置如图所示,点B的坐标为(3,4),点D是OA的中的,点E在AB上,当△CDE的周长最小时,点E的坐标为A. B. C. D.
4
