苏科版九年级数学下册期末复习 教案
图片预览



文档简介
教学内容 ①科学计数法;②一次函数和反比例函数③圆④二次函数⑤不等式的计算⑥化简求值⑦三角函数
教学过程
错题重现
1、如图,已知⊙O上依次有A、B、C、D四个点,=,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.(1)若⊙O的半径为3,∠DAB=120°,求劣弧的长;(2)求证:BF=BD;(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
知识详解
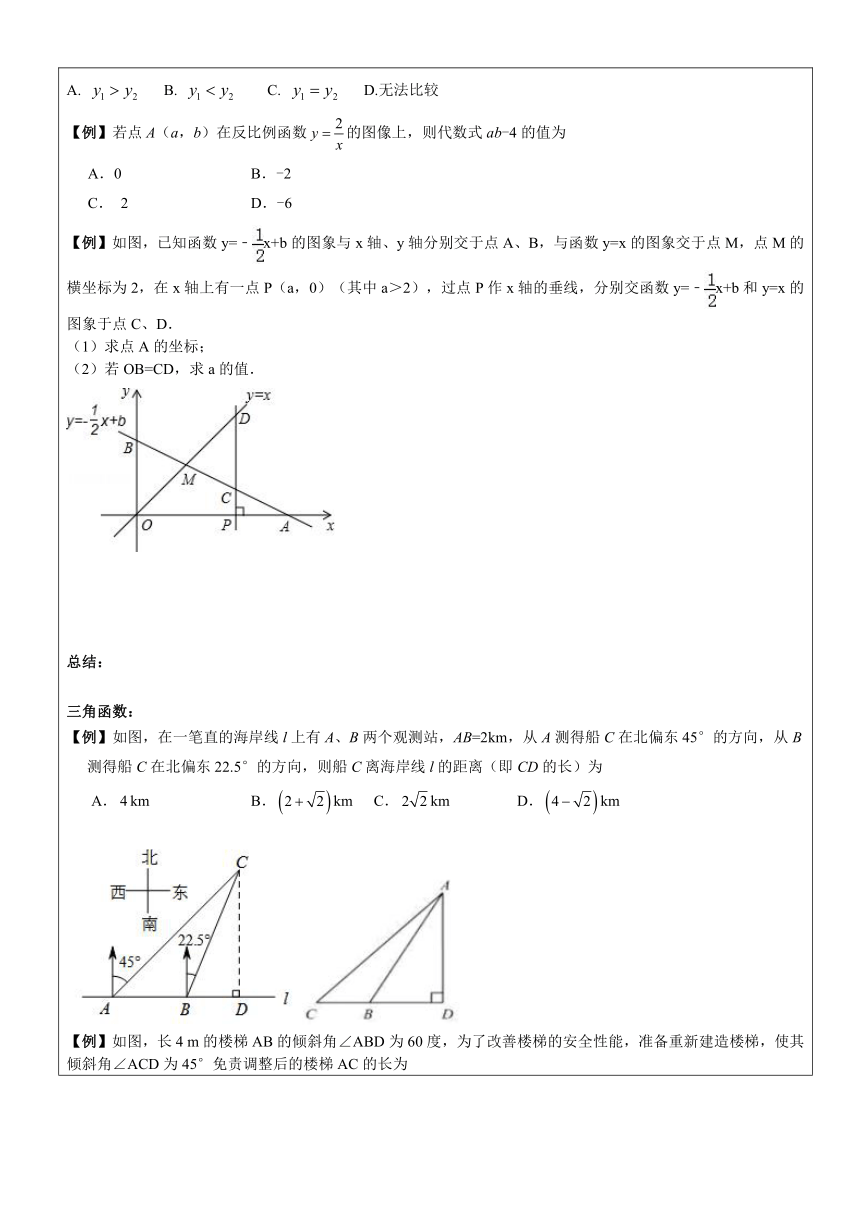
科学计数法:【例】肥皂泡的泡壁厚度大约是0.0007㎜,将0.0007用科学记数法科表示为A. B. C. D. 【例】月球的半径约为1 738 000m,1 738 000这个数用科学记数法可表示为A.1.738×106 B.1.738×107 C.0.1738×107 D.17.38×105总结:反比例函数和一次函数:【例】已知点、都是反比例函数的图像上,则、的大小关系为A. B. C. D.无法比较【例】若点A(a,b)在反比例函数的图像上,则代数式ab-4的值为A.0 B.-2 C. 2 D.-6【例】如图,已知函数y=﹣x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣x+b和y=x的图象于点C、D.(1)求点A的坐标;(2)若OB=CD,求a的值.总结:三角函数:【例】如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为A.km B.km C.km D.km【例】如图,长4 m的楼梯AB的倾斜角∠ABD为60度,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°免责调整后的楼梯AC的长为A. B. C. D. 解不等式和不等式组:【例】不等式组的最大整数解是_________.【例】解不等式,并把它的解集在数轴上表示出来.圆:【例】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为 B. C. D.【例】如图,AB是圆O的直径,D、E为圆O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD.连接AC交圆O于点F,连接AE、DE、DF.(1)证明:∠E=∠C,(2)若∠E=55°,求∠BDF的度数,(3)设DE交AB于点G,若DF=4, ,E是弧AB的中点,求的值.二次函数:【例】若二次函数y=x2+bx的图像的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 A. B. C. D.【例】已知二次函数的图象以为顶点,且过点. (1)求该函数的关系式; (2)求该函数图象与坐标轴的交点坐标; (3)将函数图象向左平移 个单位,该函数图象恰好经过原点.【例】如图,直线与轴、轴分别相交于A、B两点,抛物线经过点B. (1)求该地物线的函数表达式; (2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM.设点M的横坐标为,△ABM的面积为S.求S与的函数表达式,并求出S的最大值; (3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点. ①写出点的坐标; ②将直线绕点A按顺时针方向旋转得到直线,当直线与直线重合时停止旋转.在旋转过程中,直线与线段交于点C.设点B、到直线的距离分别为、,当最大时,求直线旋转的角度(即∠BAC的度数).
真题在线
1、计算:计算:22+|﹣1|﹣.3、解不等式组:.4、先化简,在求值:,其中.5、如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.(1)求证:ED∥AC;(2)若BD=2CD,设△EBD的面积为,△ADC的面积为,且,求△ABC的面积.
变式训练
1、计算:= .2、若,则的值为 .3、计算:.解不等式组:先化简,再求值:,其中.6、先化简,再求值:,其中.
随堂检测
1、下列关于x的方程有实数根的是( ) A.x2﹣x+1=0B.x2+x+1=0C.(x﹣1)(x+2)=0D.(x﹣1)2+1=02、二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式1﹣a﹣b的值为( ) A.﹣3B.﹣1C.2D.5已知地球的表面积约为510000000km2,数510000000用科学记数法可表示为 .4、解方程:.5、若抛物线与轴只有一个交点,求实数的值.6、已知点(3, 0)在抛物线上,求此抛物线的对称轴.7、如图,AC是⊙O的直径,PA, PB是⊙O的切线,A, B为切点,.求∠P的度数.8、已知x=1是方程的一个根,求代数式的值.9、如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( ) A.4kmB.2kmC.2kmD.(+1)km
(第5题)
4
教学过程
错题重现
1、如图,已知⊙O上依次有A、B、C、D四个点,=,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.(1)若⊙O的半径为3,∠DAB=120°,求劣弧的长;(2)求证:BF=BD;(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
知识详解
科学计数法:【例】肥皂泡的泡壁厚度大约是0.0007㎜,将0.0007用科学记数法科表示为A. B. C. D. 【例】月球的半径约为1 738 000m,1 738 000这个数用科学记数法可表示为A.1.738×106 B.1.738×107 C.0.1738×107 D.17.38×105总结:反比例函数和一次函数:【例】已知点、都是反比例函数的图像上,则、的大小关系为A. B. C. D.无法比较【例】若点A(a,b)在反比例函数的图像上,则代数式ab-4的值为A.0 B.-2 C. 2 D.-6【例】如图,已知函数y=﹣x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣x+b和y=x的图象于点C、D.(1)求点A的坐标;(2)若OB=CD,求a的值.总结:三角函数:【例】如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为A.km B.km C.km D.km【例】如图,长4 m的楼梯AB的倾斜角∠ABD为60度,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°免责调整后的楼梯AC的长为A. B. C. D. 解不等式和不等式组:【例】不等式组的最大整数解是_________.【例】解不等式,并把它的解集在数轴上表示出来.圆:【例】如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为 B. C. D.【例】如图,AB是圆O的直径,D、E为圆O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD.连接AC交圆O于点F,连接AE、DE、DF.(1)证明:∠E=∠C,(2)若∠E=55°,求∠BDF的度数,(3)设DE交AB于点G,若DF=4, ,E是弧AB的中点,求的值.二次函数:【例】若二次函数y=x2+bx的图像的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为 A. B. C. D.【例】已知二次函数的图象以为顶点,且过点. (1)求该函数的关系式; (2)求该函数图象与坐标轴的交点坐标; (3)将函数图象向左平移 个单位,该函数图象恰好经过原点.【例】如图,直线与轴、轴分别相交于A、B两点,抛物线经过点B. (1)求该地物线的函数表达式; (2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM.设点M的横坐标为,△ABM的面积为S.求S与的函数表达式,并求出S的最大值; (3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点. ①写出点的坐标; ②将直线绕点A按顺时针方向旋转得到直线,当直线与直线重合时停止旋转.在旋转过程中,直线与线段交于点C.设点B、到直线的距离分别为、,当最大时,求直线旋转的角度(即∠BAC的度数).
真题在线
1、计算:计算:22+|﹣1|﹣.3、解不等式组:.4、先化简,在求值:,其中.5、如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.(1)求证:ED∥AC;(2)若BD=2CD,设△EBD的面积为,△ADC的面积为,且,求△ABC的面积.
变式训练
1、计算:= .2、若,则的值为 .3、计算:.解不等式组:先化简,再求值:,其中.6、先化简,再求值:,其中.
随堂检测
1、下列关于x的方程有实数根的是( ) A.x2﹣x+1=0B.x2+x+1=0C.(x﹣1)(x+2)=0D.(x﹣1)2+1=02、二次函数y=ax2+bx﹣1(a≠0)的图象经过点(1,1),则代数式1﹣a﹣b的值为( ) A.﹣3B.﹣1C.2D.5已知地球的表面积约为510000000km2,数510000000用科学记数法可表示为 .4、解方程:.5、若抛物线与轴只有一个交点,求实数的值.6、已知点(3, 0)在抛物线上,求此抛物线的对称轴.7、如图,AC是⊙O的直径,PA, PB是⊙O的切线,A, B为切点,.求∠P的度数.8、已知x=1是方程的一个根,求代数式的值.9、如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( ) A.4kmB.2kmC.2kmD.(+1)km
(第5题)
4
同课章节目录
