7.4.1二项分布课件——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共17张PPT)
文档属性
| 名称 | 7.4.1二项分布课件——2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:03:19 | ||
图片预览






文档简介
(共17张PPT)
7.4二项分布与超几何分布7.4.1二项分布学习目标(1分钟)1.了解伯努利试验2.掌握二项分布及其数字特征,并能解决简单的实际问题问题导学(4分钟)
自学教材P72-76页内容,思考以下问题:
问题1:什么是伯努利试验和n重伯努利试验?
问题2:二项分布的定义?
问题3:二项分布的均值和方差各是什么?
1.抛一枚硬币的结果
2.检验一个产品是否为合格品
3.射击中靶或者脱靶
以上问题有哪些共同特征?
我们把只包含两个可能结果的试验叫做伯努利试验。
1.伯努利试验
点拨精讲(24分钟)
2.n重伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验成为n重伯努利试验。
n重伯努利试验具有如下共同的特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验结果相互独立。
各次试验成功的概率相同
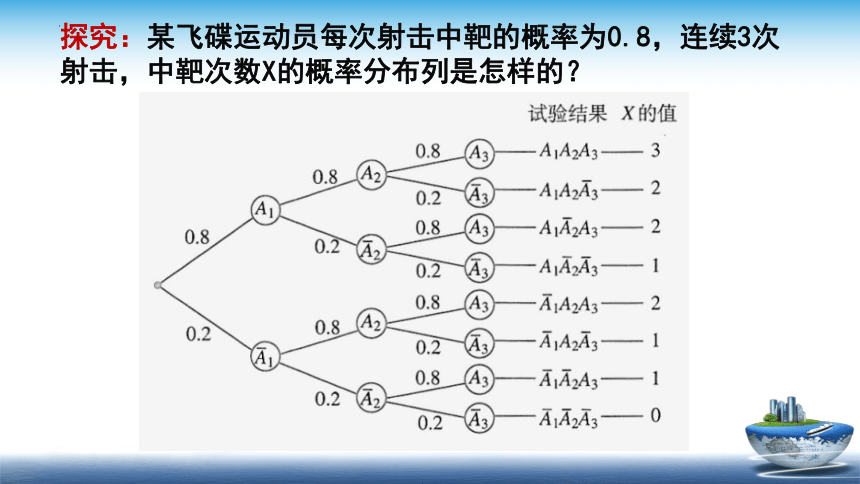
探究:某飞碟运动员每次射击中靶的概率为0.8,连续3次射击,中靶次数X的概率分布列是怎样的?
3.二项分布
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1) 恰好出现5次正面朝上的概率;
(2) 正面朝上出现的频率在[0.4, 0.6]内的概率.
解:
设A=“正面朝上”,则P(A)=0.5. 用X表示事件A发生的次数,
则 X ~ B(10, 0.5).
(1) 恰好出现5次正面朝上的概率为
(2) 正面朝上出现的频率在[0.4, 0.60内等价于4≤X≤6,于是所求概率为
随机变量X服从二项分布的三个前提条件:
(1) 每次试验都是在同一条件下进行的;
(2) 每一次试验都彼此相互独立;
(3) 每次试验出现的结果只有两个,即某事件要么发生,要么不发生.
只有这三个条件均满足时才能说明随机变量X服从二项分布,其事件A在n次独立重复试验中恰好发生k次的概率可用下面公式计算.
归纳:一般地,确定一个二项分布模型的步骤如下:(1) 明确伯努利试验及事件A的意义,确定事件A发生的概率p;(2) 确定重复试验的次数n,并判断各次试验的独立性;(3) 设X为n次独立重复试验中事件A发生的次数,则X~B(n,p).若X~B(n, p),则有
二项分布的均值与方差
下面对均值进行证明.
证明:
√课堂小结(1分钟)1.伯努利和n重伯努利试验:2.二项分布:3.二项分布的均值和方差:当堂检测(15分钟)
1.某气象站天气预报的准确率为80%,计算(结果保留到小数点后第2位):
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
√
解
n重伯努利试验概率求解的三个步骤
(1)判断:依据n重伯努利试验的特征,判断所给试验是否为伯努利试验.
(2)分拆:判断所求事件是否需要分拆.
(3)计算:就每个事件依据n重伯努利试验的概率公式求解,最后利用互斥事件的概率加法公式计算.
3.
7.4二项分布与超几何分布7.4.1二项分布学习目标(1分钟)1.了解伯努利试验2.掌握二项分布及其数字特征,并能解决简单的实际问题问题导学(4分钟)
自学教材P72-76页内容,思考以下问题:
问题1:什么是伯努利试验和n重伯努利试验?
问题2:二项分布的定义?
问题3:二项分布的均值和方差各是什么?
1.抛一枚硬币的结果
2.检验一个产品是否为合格品
3.射击中靶或者脱靶
以上问题有哪些共同特征?
我们把只包含两个可能结果的试验叫做伯努利试验。
1.伯努利试验
点拨精讲(24分钟)
2.n重伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验成为n重伯努利试验。
n重伯努利试验具有如下共同的特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验结果相互独立。
各次试验成功的概率相同
探究:某飞碟运动员每次射击中靶的概率为0.8,连续3次射击,中靶次数X的概率分布列是怎样的?
3.二项分布
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1) 恰好出现5次正面朝上的概率;
(2) 正面朝上出现的频率在[0.4, 0.6]内的概率.
解:
设A=“正面朝上”,则P(A)=0.5. 用X表示事件A发生的次数,
则 X ~ B(10, 0.5).
(1) 恰好出现5次正面朝上的概率为
(2) 正面朝上出现的频率在[0.4, 0.60内等价于4≤X≤6,于是所求概率为
随机变量X服从二项分布的三个前提条件:
(1) 每次试验都是在同一条件下进行的;
(2) 每一次试验都彼此相互独立;
(3) 每次试验出现的结果只有两个,即某事件要么发生,要么不发生.
只有这三个条件均满足时才能说明随机变量X服从二项分布,其事件A在n次独立重复试验中恰好发生k次的概率可用下面公式计算.
归纳:一般地,确定一个二项分布模型的步骤如下:(1) 明确伯努利试验及事件A的意义,确定事件A发生的概率p;(2) 确定重复试验的次数n,并判断各次试验的独立性;(3) 设X为n次独立重复试验中事件A发生的次数,则X~B(n,p).若X~B(n, p),则有
二项分布的均值与方差
下面对均值进行证明.
证明:
√课堂小结(1分钟)1.伯努利和n重伯努利试验:2.二项分布:3.二项分布的均值和方差:当堂检测(15分钟)
1.某气象站天气预报的准确率为80%,计算(结果保留到小数点后第2位):
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
√
解
n重伯努利试验概率求解的三个步骤
(1)判断:依据n重伯努利试验的特征,判断所给试验是否为伯努利试验.
(2)分拆:判断所求事件是否需要分拆.
(3)计算:就每个事件依据n重伯努利试验的概率公式求解,最后利用互斥事件的概率加法公式计算.
3.
