青岛版七年级下册9.3角的度量导学案

9.3 《角的度量》导学案
东坝初中 夏萍 审核：刘荣华
一、教学目标
1．理解互为余角、互为补角的定义．
2．掌握有关补角和余角的性质．
3．应用以上知识点解决有关计算和简单推理问题．
二、教学重点、难点与疑点
(一)重点：互为余角、互为补角的角的概念及有关余角、补角的性质．
(二)难点：有关余角和有关补角性质的导出．
(三)疑点：互余、互补的两个角图形的位置关系．
三、教学方法
引导发现、尝试指导相结合．
四、教具准备
三角板、量角器．
五、教学步骤
(一)创设情境，引出课题
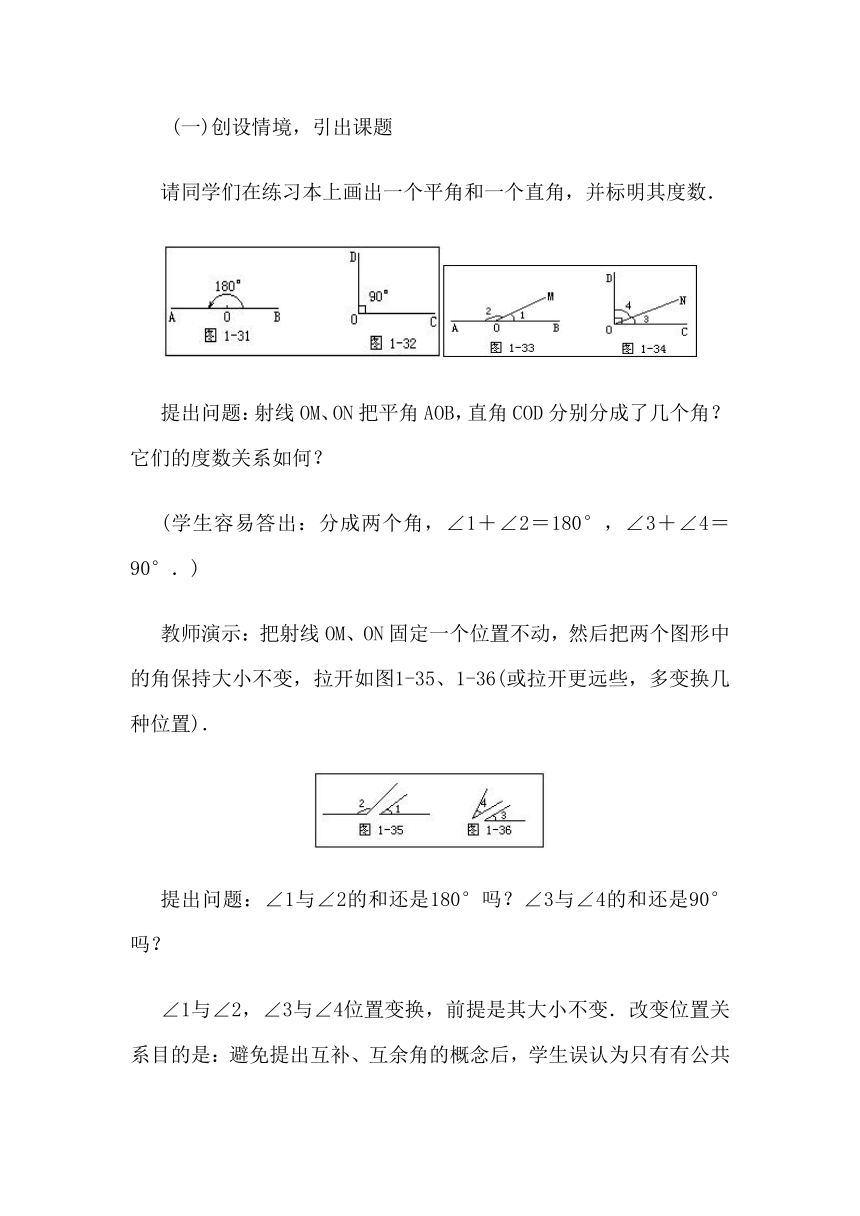
请同学们在练习本上画出一个平角和一个直角，并标明其度数．
提出问题：射线OM、ON把平角AOB，直角COD分别分成了几个角？它们的度数关系如何？
(学生容易答出：分成两个角，∠1＋∠2＝180°，∠3＋∠4＝90°．)
教师演示：把射线OM、ON固定一个位置不动，然后把两个图形中的角保持大小不变，拉开如图1-35、1-36(或拉开更远些，多变换几种位置)．
提出问题：∠1与∠2的和还是180°吗？∠3与∠4的和还是90°吗？
∠1与∠2，∠3与∠4位置变换，前提是其大小不变．改变位置关系目的是：避免提出互补、互余角的概念后，学生误认为只有有公共顶点且和为180°，90°的两个角才是互补，互余的角．
根据学生回答，教师肯定结论：
不论∠1、∠2、∠3、∠4的位置关系如何变化，只要大小不变，∠1与∠2的和永远是平角，∠3与∠4的和永远是直角．象这样具有特殊关系的角，我们分别叫它们互为补角和互为余角．这就是我们要学习的角的度量一节中又一新知识．(板书课题)
(二)探索新知
1．互为余角、互为补角的定义
互为余角：如果两个角的和是一个直角，那么这两个角叫互为余角．其中一个角叫做另一个角的余角．
互为补角：如果两个角的和是一个平角，那么这两个角叫互为补角．其中一个角叫做另一个角的补角．
提出问题，理解定义．
(1)以上定义中的“互为”是什么意思？
(2)若∠1＋∠2＋∠3＝180°，那么∠1、∠2、∠3互为补角吗？
(3)互为余角、互为补角的两个角是否一定有公共顶点？
2．概念应用
一个角的补角是它的3倍，求这个角．
变式训练：
一个角的余角是它的3倍，求这个角．
一个角是它的补角的3倍，求这个角．
有关互余、互补角的性质
同角或等角的余角相等
同角或等角的补角相等．
(三)归纳总结
以提问的形式列出下表
思考题
1．锐角的余角一定是锐角吗？
2．一个角的补角比这个角的余角大多少度？
3．相等且互补的两个角各是多少度？
巩固练习：

巩固练习：
六、布置作业
习题9.3 A组1，2