青岛版七年级下册9.5垂直导学案

9.5《垂直》导学案
黄楼初中 主备：潘娇丽 毕玉华 审核：郝希学 刘荣华
课本内容：P16—17
课前准备：三角尺 量角器
学习目标：
使学生理解垂线的意义和垂线的两个性质。
会用三角板和量角器过一点画已知直线的垂线，培养学生掌握画图的基本技能。
通过垂线性质的学习，培养学生发现问题的能力。
学习重点和难点：
重点：认识垂线、掌握画垂线的方法。
难点：能正确、规范地画出已知直线的垂线。
知识回顾：
说出互余、互补的定义
对顶角的性质是什么？
已知：直线AB与直线CD相交，交点为O,若∠AOB=90°,则∠BOD、∠COB、∠COA的度数分别是多少？并说明理由。
学习过程：
导入新课
由知识回顾3中直线AB与直线CD的位置关系是相交的一种特殊情况—垂直导入。
新知学习
垂直定义
自学要求：认真阅读课本16页实验与探究前面部分。并完成学案：
就说这两条直线互相垂直，其中一条直线叫做另一条直线的 。
如图：直线AB与CD互相垂直，记作＿＿＿或＿＿＿，交点O叫做＿＿＿。
垂线的性质1
自学要求：自学课本16页实验与探究，并与同学交流用三角板和量角器过一点（包括点在直线上和点在直线外两种情况）画已知直线垂线的步骤。
步骤：
通过操作发现垂线的性质1：
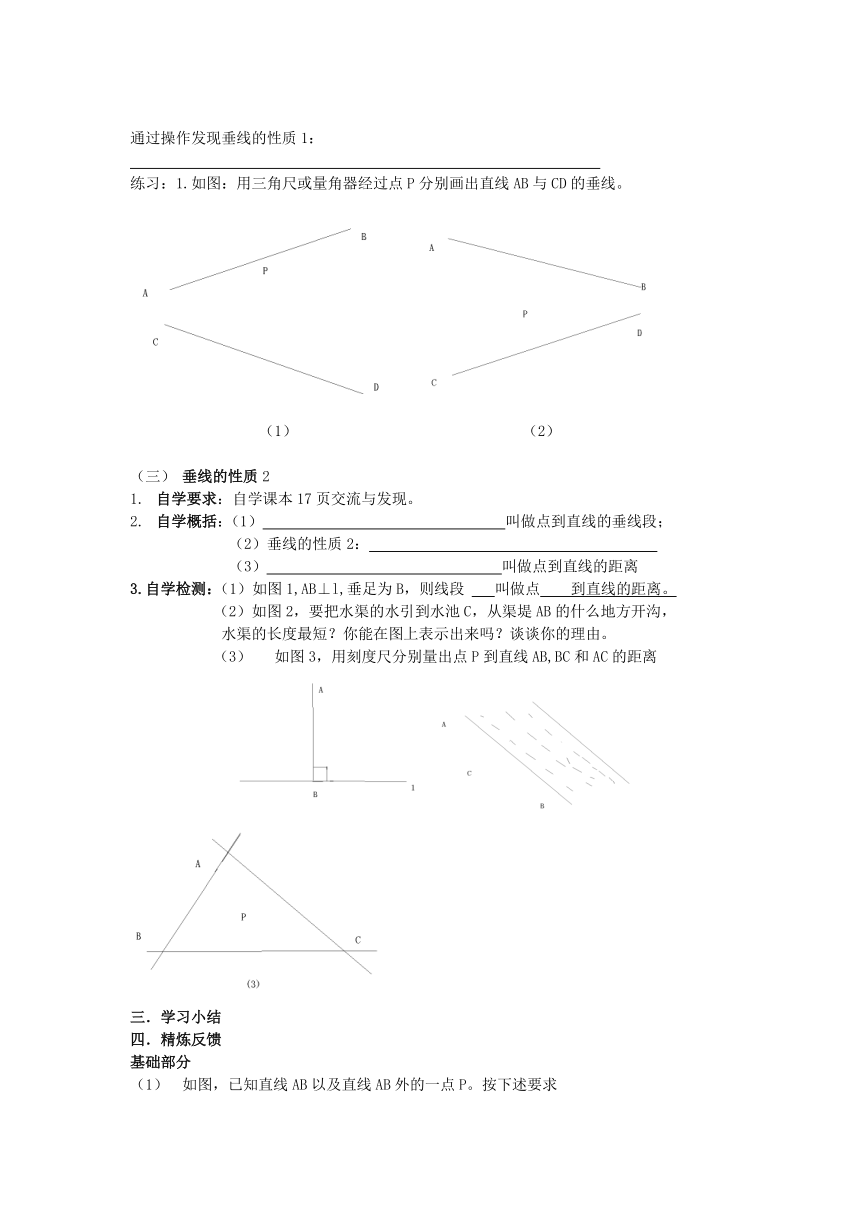
练习：1.如图：用三角尺或量角器经过点P分别画出直线AB与CD的垂线。
（1） （2）
垂线的性质2
自学要求：自学课本17页交流与发现。
自学概括：（1） 叫做点到直线的垂线段；
（2）垂线的性质2：
（3） 叫做点到直线的距离
3.自学检测：（1）如图1,AB⊥l,垂足为B，则线段 叫做点 到直线的距离。
（2）如图2，要把水渠的水引到水池C，从渠堤AB的什么地方开沟，
水渠的长度最短？你能在图上表示出来吗？谈谈你的理由。
（3） 如图3，用刻度尺分别量出点P到直线AB,BC和AC的距离
三．学习小结
四．精炼反馈
基础部分
如图，已知直线AB以及直线AB外的一点P。按下述要求
画图并填空：
过点P画PC⊥AB,垂足为点C;
点P到直线AB的距离是线段 的长度
点P到直线AB的距离为 （精确到1mm）
(2)如图所示，计划把河中的水引到水池C中，可过C作CD⊥AB，垂足为D，然后沿CD
开渠，则能使所开渠最短，这样设计的依据是
画∠AOB=45°，在∠AOB内找一点F,过F点作OA,OB的垂线
画∠AOB=120°，画∠AOB的平分线OE，在OE上任取一点F，过F作OA,OB的垂线，
垂足分别为G、H，并测量FG、FH的长度，你有什么发现。
能力提高
1、如图，∠1和∠2满足 时，能使OA⊥OB
2、两块直角三角板的直角顶点重合为如图所示的形状，若∠AOD=135°，则∠BOC=
3.直线ｌ外一点Ｐ与直线上的一点Ｑ的距离是２ｃｍ，则点Ｐ到直线ｌ的距离是（　　）
Ａ.等于２ｃｍ B.小于２ｃｍ C.不大于２ｃｍ D.大于２ｃｍ
4.如图所示，O点是直线AB上的一点，DO⊥AB,CO⊥EO,那么下列各式中错误的是（ ）
A.∠AOC=∠DOE B.∠COD=∠EOB C.∠BOC+∠DOE=180° D.∠AOC=∠BOC
5.上题中，∠COD=40°,则∠COB的度数是（ ）
6.体育课上，怎样测量跳远成绩，并说明理由。
知识拓展
学校的位置如图所示，请设计出学校到两条公路的最短距离的方案，并在图上标出来，并说明理由 。