苏教版数学六年级上册一 长方体和正方体 综合素质达标(含答案)
文档属性
| 名称 | 苏教版数学六年级上册一 长方体和正方体 综合素质达标(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 66.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 00:00:00 | ||
图片预览




文档简介
第一单元综合素质达标
一、填空。(每空1分,共23分)
1.在括号里填上合适的单位名称。
学校旗杆高14.8( )。
一块橡皮的体积是6.4( )。
一个游泳池蓄水约是50( )。
一个热水瓶的容积是2( )。
2.1270立方厘米=( )毫升=( )升
0.42立方分米=( )立方厘米
3050毫升=( )升( )毫升
3.5立方米=( )立方分米
3.小新家有两块长5分米、宽3分米的玻璃,两块长4分米、宽3分米的玻璃,他爸爸想做一个无盖的长方体玻璃鱼缸,还要配一块长( )分米、宽( )分米的玻璃。
4.一个长方体的表面积是40平方厘米,把它平均分开,正好分成两个相同的正方体,每个正方体的表面积是( )平方厘米,这个长方体的体积是( )立方厘米。
5.用相同长度的铁丝分别做一个长方体和一个正方体框架,正方体框架的棱长是8厘米,长方体框架的长是1分米,宽是7厘米,高是( )厘米。
6.把一个棱长为4分米的正方体木料锯成3个相同的长方体,表面积增加了( )平方分米。
7.把一个长124厘米、宽10厘米、高10厘米的长方体锯成最大的正方体,最多可锯成( )个。(每个正方体的大小相同)
8.把一个长10厘米、宽8厘米、高6厘米的长方体锯成两个小长方体,表面积最少增加( )平方厘米,最多增加( )平方
厘米。
9.饭店烟囱的横截面是边长为1分米的正方形,如果每节长2米,那么做20节这样的烟囱至少需要铁皮( )平方米。
10.小华观察一个模型(由棱长为1厘米的小正方体拼成),分别从前面、上面、右面观察,看到的图形如下图所示,那么该模型的体积是( )立方厘米。
11.用24个棱长是1厘米的小正方体摆成不同的长方体,表面积最小是( )平方厘米,体积是( )立方厘米。
二、判断。(对的画“√”,错的画“×”)(每题1分,共5分)
1.一个长方体,将它的长、宽、高分别减少1分米,那么它的体积比原来减少1立方分米。 ( )
2.墨水瓶上有“净含量60毫升”的字样,这个60毫升是指墨水瓶的容积。 ( )
3.如果两个正方体的体积相等,那么它们的表面积也相等。( )
4.如果长方体和正方体的底面积与高分别相等,那么它们的表面积也相等。 ( )
5.棱长是6厘米的正方体的表面积和体积相等。 ( )
三、选择。(将正确答案的字母填在括号里)(每题2分,共10分)
1.如果把一个长方体纸盒的表面完全展开,至少要剪开( )
条棱。
A.5 B.6 C.7 D.8
2.一个长方体的长、宽、高分别是a米、b米、h米,如果高增加2米后,新的长方体的表面积比原来增加了( )平方米。
A.ab(h+b) B.(a+b)×2
C.(a+b)×4 D.2ab
3.一个长方体盒子从里面量长6厘米,宽4厘米,高5厘米,往里面放棱长为2厘米的小正方体,最多可以放( )个。
A.12 B.15 C.18 D.10
4.下图中,哪一个能折叠成一个正方体?( )
5.把一个表面涂色的正方体分割成若干个体积为1立方厘米的小正方体,其中两面涂色的小正方体有36个,一面涂色的小正方体有几个?原来正方体的体积是多少立方厘米?正确的选项是( )。
A.8 64 B.54 125
C.27 216 D.54 27
四、计算。(共14分)
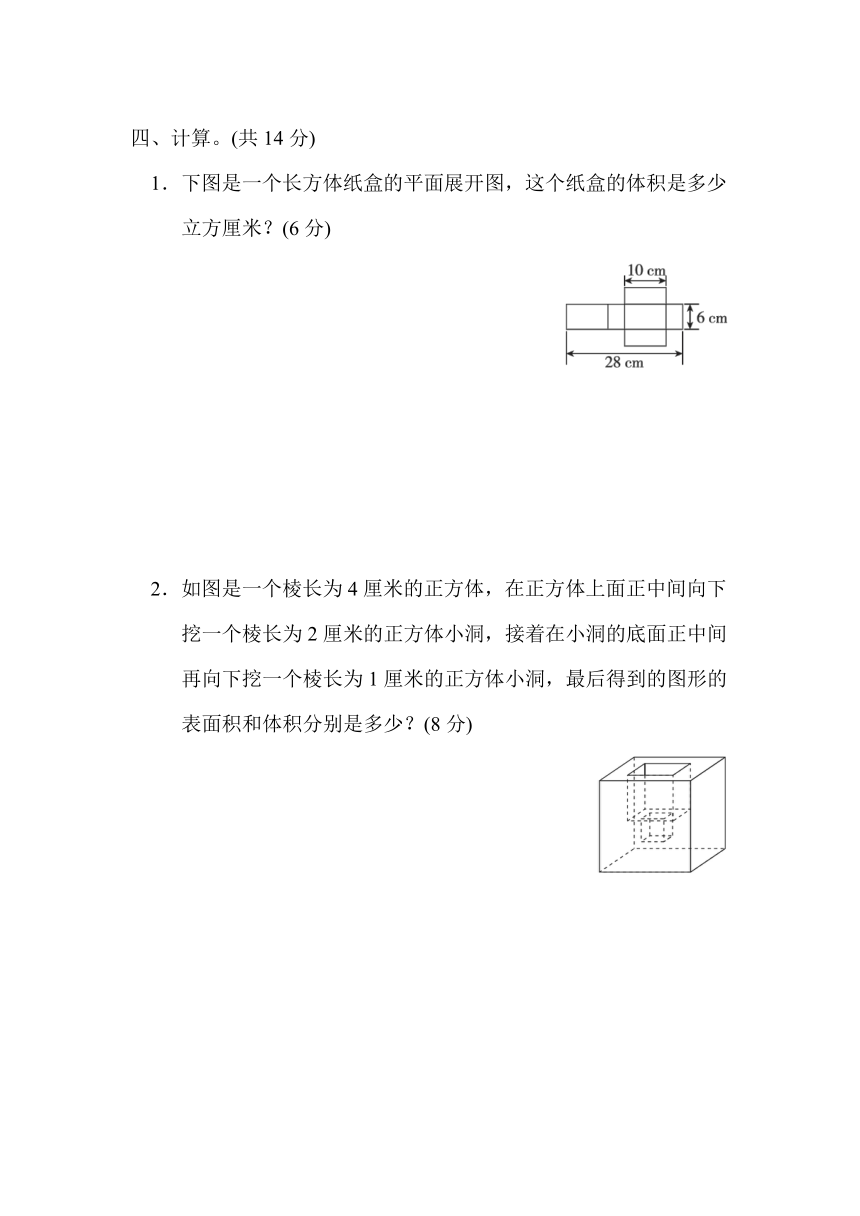
1.下图是一个长方体纸盒的平面展开图,这个纸盒的体积是多少立方厘米?(6分)
2.如图是一个棱长为4厘米的正方体,在正方体上面正中间向下挖一个棱长为2厘米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长为1厘米的正方体小洞,最后得到的图形的表面积和体积分别是多少?(8分)
五、动手操作。(16分)
1.将如图的长方形铁皮剪成5块,焊成一个底面是正方形的无盖长方体容器,所焊容器的容积是多少?(铁皮厚度忽略不计)
(6分)
2.用棱长为1 cm 的小正方体按下面的规律摆长方体。
……
(1)用3个小正方体摆成的长方体的表面积是( )cm2,体积是( )cm3。(4分)
(2)用n个小正方体摆成的长方体的表面积是( )cm2,体积是( )cm3。(4分)
(3)用( )个小正方体摆成的长方体的表面积是22 cm2。(2分)
六、解决问题。(共32分)
1.一个长方体汽油箱,长和宽都是6 dm,高是5 dm。 (1)做这个汽油箱至少需要多少平方分米的铁皮?(3分)
(2)如果每升汽油的价格是5.5元,将这个空汽油箱加满汽油一
共要付多少元?(3分)
2.一盒牛奶的外包装上标有“净含量200 mL”的字样,小明动手量了一下,发现盒子从外面量长5 cm,宽4 cm,高10 cm,你觉得这个标注合适吗?为什么?(5分)
3.一个底面是正方形的长方体,表面积是170平方厘米。如果用一个平行于底面的平面将它截成两个长方体,则两个长方体的表面积之和是220平方厘米。原来长方体的体积是多少立方厘米?(6分)
4.在一个长25 cm、宽12 cm、高20 cm的长方体玻璃缸中放入一个棱长是9 cm的正方体铁块,加水使铁块完全浸没在水中。当铁块从水中取出后,玻璃缸中的水下降了多少厘米?(6分)
5.我们知道要把一个长方体切成两个完全相同的小长方体,有三种不同的切法,若这三种切法,增加的表面积分别是84 cm2,70 cm2,60 cm2。
(1)你知道原来这个长方体的表面积吗?(4分)
(2)原来这个长方体的体积是多少?(5分)
答案
一、1.米 立方厘米 立方米 升
2.1270 1.27 420 3 50 3500
3.5 4 4.24 16
5.7 6.64 7.12
8.96 160 9.16
10.5 11.52 24
二、1.× 2.× 3.√ 4.× 5.×
三、1.C 2.C 3.A 4.A 5.B
四、1.高:(28-10×2)÷2=4(cm)
体积:4×10×6=240(cm3)
2.表面积:6×4×4+4×2×2+4×1×1=116(平方厘米)
体积:4×4×4-2×2×2-1×1×1=55(立方厘米)
五、1.
(40-20)÷4=5(dm)
20×20×5=2000(dm3)
2.(1)14 3
(2)4n+2 n
(3)5
六、1.(1)6×6×2+6×5×4=192(dm2)
答:做这个汽油箱至少需要192 dm2的铁皮。
(2)6×6×5=180(dm3)
180 dm3=180 L
180×5.5=990(元)
答:将这个空汽油箱加满汽油一共要付990元。
2.5×4×10=200(cm3)
200 cm3=200 mL
答:不合适,因为盒子有厚度。
3.(220-170)÷2=25(平方厘米)
25=5×5
(170-25×2)÷(5×4)=6(厘米)
25×6=150(立方厘米)
答:原来长方体的体积是150立方厘米。
4.(9×9×9)÷(25×12)=2.43(cm)
答:玻璃缸中的水会下降2.43 cm。
5.(1)84+70+60=214(cm2)
答:原来这个长方体的表面积是214 cm2。
(2)84÷2=42(cm2)
70÷2=35(cm2)
60÷2=30(cm2)
42=6×7 35=5×7 30=6×5
5×6×7=210(cm3)
答:原来这个长方体的体积是210 cm3。
4/ 10
一、填空。(每空1分,共23分)
1.在括号里填上合适的单位名称。
学校旗杆高14.8( )。
一块橡皮的体积是6.4( )。
一个游泳池蓄水约是50( )。
一个热水瓶的容积是2( )。
2.1270立方厘米=( )毫升=( )升
0.42立方分米=( )立方厘米
3050毫升=( )升( )毫升
3.5立方米=( )立方分米
3.小新家有两块长5分米、宽3分米的玻璃,两块长4分米、宽3分米的玻璃,他爸爸想做一个无盖的长方体玻璃鱼缸,还要配一块长( )分米、宽( )分米的玻璃。
4.一个长方体的表面积是40平方厘米,把它平均分开,正好分成两个相同的正方体,每个正方体的表面积是( )平方厘米,这个长方体的体积是( )立方厘米。
5.用相同长度的铁丝分别做一个长方体和一个正方体框架,正方体框架的棱长是8厘米,长方体框架的长是1分米,宽是7厘米,高是( )厘米。
6.把一个棱长为4分米的正方体木料锯成3个相同的长方体,表面积增加了( )平方分米。
7.把一个长124厘米、宽10厘米、高10厘米的长方体锯成最大的正方体,最多可锯成( )个。(每个正方体的大小相同)
8.把一个长10厘米、宽8厘米、高6厘米的长方体锯成两个小长方体,表面积最少增加( )平方厘米,最多增加( )平方
厘米。
9.饭店烟囱的横截面是边长为1分米的正方形,如果每节长2米,那么做20节这样的烟囱至少需要铁皮( )平方米。
10.小华观察一个模型(由棱长为1厘米的小正方体拼成),分别从前面、上面、右面观察,看到的图形如下图所示,那么该模型的体积是( )立方厘米。
11.用24个棱长是1厘米的小正方体摆成不同的长方体,表面积最小是( )平方厘米,体积是( )立方厘米。
二、判断。(对的画“√”,错的画“×”)(每题1分,共5分)
1.一个长方体,将它的长、宽、高分别减少1分米,那么它的体积比原来减少1立方分米。 ( )
2.墨水瓶上有“净含量60毫升”的字样,这个60毫升是指墨水瓶的容积。 ( )
3.如果两个正方体的体积相等,那么它们的表面积也相等。( )
4.如果长方体和正方体的底面积与高分别相等,那么它们的表面积也相等。 ( )
5.棱长是6厘米的正方体的表面积和体积相等。 ( )
三、选择。(将正确答案的字母填在括号里)(每题2分,共10分)
1.如果把一个长方体纸盒的表面完全展开,至少要剪开( )
条棱。
A.5 B.6 C.7 D.8
2.一个长方体的长、宽、高分别是a米、b米、h米,如果高增加2米后,新的长方体的表面积比原来增加了( )平方米。
A.ab(h+b) B.(a+b)×2
C.(a+b)×4 D.2ab
3.一个长方体盒子从里面量长6厘米,宽4厘米,高5厘米,往里面放棱长为2厘米的小正方体,最多可以放( )个。
A.12 B.15 C.18 D.10
4.下图中,哪一个能折叠成一个正方体?( )
5.把一个表面涂色的正方体分割成若干个体积为1立方厘米的小正方体,其中两面涂色的小正方体有36个,一面涂色的小正方体有几个?原来正方体的体积是多少立方厘米?正确的选项是( )。
A.8 64 B.54 125
C.27 216 D.54 27
四、计算。(共14分)
1.下图是一个长方体纸盒的平面展开图,这个纸盒的体积是多少立方厘米?(6分)
2.如图是一个棱长为4厘米的正方体,在正方体上面正中间向下挖一个棱长为2厘米的正方体小洞,接着在小洞的底面正中间再向下挖一个棱长为1厘米的正方体小洞,最后得到的图形的表面积和体积分别是多少?(8分)
五、动手操作。(16分)
1.将如图的长方形铁皮剪成5块,焊成一个底面是正方形的无盖长方体容器,所焊容器的容积是多少?(铁皮厚度忽略不计)
(6分)
2.用棱长为1 cm 的小正方体按下面的规律摆长方体。
……
(1)用3个小正方体摆成的长方体的表面积是( )cm2,体积是( )cm3。(4分)
(2)用n个小正方体摆成的长方体的表面积是( )cm2,体积是( )cm3。(4分)
(3)用( )个小正方体摆成的长方体的表面积是22 cm2。(2分)
六、解决问题。(共32分)
1.一个长方体汽油箱,长和宽都是6 dm,高是5 dm。 (1)做这个汽油箱至少需要多少平方分米的铁皮?(3分)
(2)如果每升汽油的价格是5.5元,将这个空汽油箱加满汽油一
共要付多少元?(3分)
2.一盒牛奶的外包装上标有“净含量200 mL”的字样,小明动手量了一下,发现盒子从外面量长5 cm,宽4 cm,高10 cm,你觉得这个标注合适吗?为什么?(5分)
3.一个底面是正方形的长方体,表面积是170平方厘米。如果用一个平行于底面的平面将它截成两个长方体,则两个长方体的表面积之和是220平方厘米。原来长方体的体积是多少立方厘米?(6分)
4.在一个长25 cm、宽12 cm、高20 cm的长方体玻璃缸中放入一个棱长是9 cm的正方体铁块,加水使铁块完全浸没在水中。当铁块从水中取出后,玻璃缸中的水下降了多少厘米?(6分)
5.我们知道要把一个长方体切成两个完全相同的小长方体,有三种不同的切法,若这三种切法,增加的表面积分别是84 cm2,70 cm2,60 cm2。
(1)你知道原来这个长方体的表面积吗?(4分)
(2)原来这个长方体的体积是多少?(5分)
答案
一、1.米 立方厘米 立方米 升
2.1270 1.27 420 3 50 3500
3.5 4 4.24 16
5.7 6.64 7.12
8.96 160 9.16
10.5 11.52 24
二、1.× 2.× 3.√ 4.× 5.×
三、1.C 2.C 3.A 4.A 5.B
四、1.高:(28-10×2)÷2=4(cm)
体积:4×10×6=240(cm3)
2.表面积:6×4×4+4×2×2+4×1×1=116(平方厘米)
体积:4×4×4-2×2×2-1×1×1=55(立方厘米)
五、1.
(40-20)÷4=5(dm)
20×20×5=2000(dm3)
2.(1)14 3
(2)4n+2 n
(3)5
六、1.(1)6×6×2+6×5×4=192(dm2)
答:做这个汽油箱至少需要192 dm2的铁皮。
(2)6×6×5=180(dm3)
180 dm3=180 L
180×5.5=990(元)
答:将这个空汽油箱加满汽油一共要付990元。
2.5×4×10=200(cm3)
200 cm3=200 mL
答:不合适,因为盒子有厚度。
3.(220-170)÷2=25(平方厘米)
25=5×5
(170-25×2)÷(5×4)=6(厘米)
25×6=150(立方厘米)
答:原来长方体的体积是150立方厘米。
4.(9×9×9)÷(25×12)=2.43(cm)
答:玻璃缸中的水会下降2.43 cm。
5.(1)84+70+60=214(cm2)
答:原来这个长方体的表面积是214 cm2。
(2)84÷2=42(cm2)
70÷2=35(cm2)
60÷2=30(cm2)
42=6×7 35=5×7 30=6×5
5×6×7=210(cm3)
答:原来这个长方体的体积是210 cm3。
4/ 10
