15.2旋转 课件
图片预览






文档简介
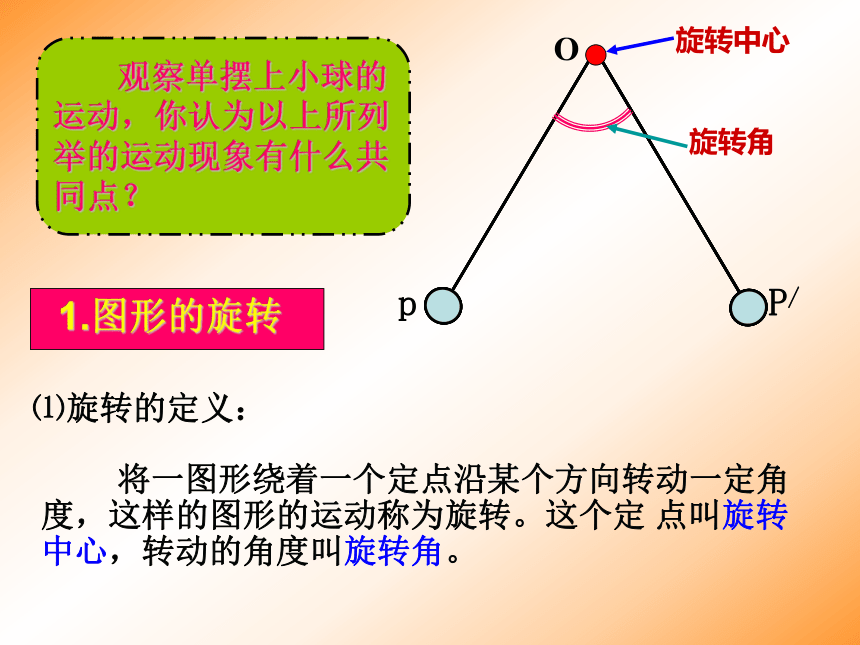
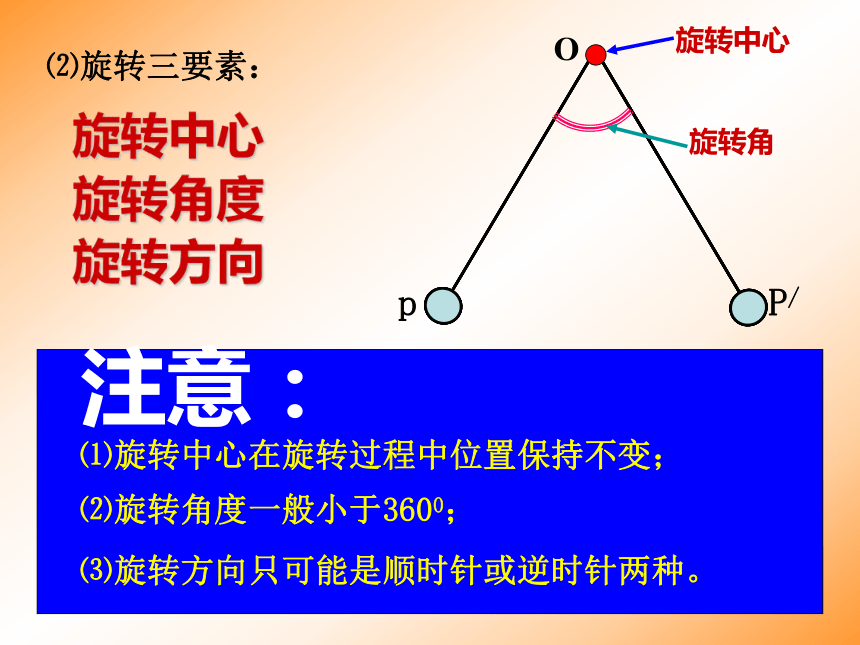
课件46张PPT。制作:遂宁一中HDL华东师大版七年级下册《数学》10.3旋转(第1课时) 在日常生活中,除了物体的平移现象。下面的图片中物体在作什么运动?由一个或几个基本图形旋转而产生的奇妙图案pP/O 观察单摆上小球的运动,你认为以上所列举的运动现象有什么共同点?⑴旋转的定义: 将一图形绕着一个定点沿某个方向转动一定角度,这样的图形的运动称为旋转。这个定 点叫旋转中心,转动的角度叫旋转角。pP/O⑴旋转中心在旋转过程中位置保持不变;⑵旋转角度一般小于3600;⑶旋转方向只可能是顺时针或逆时针两种。 ⑵旋转三要素:旋转中心
旋转角度
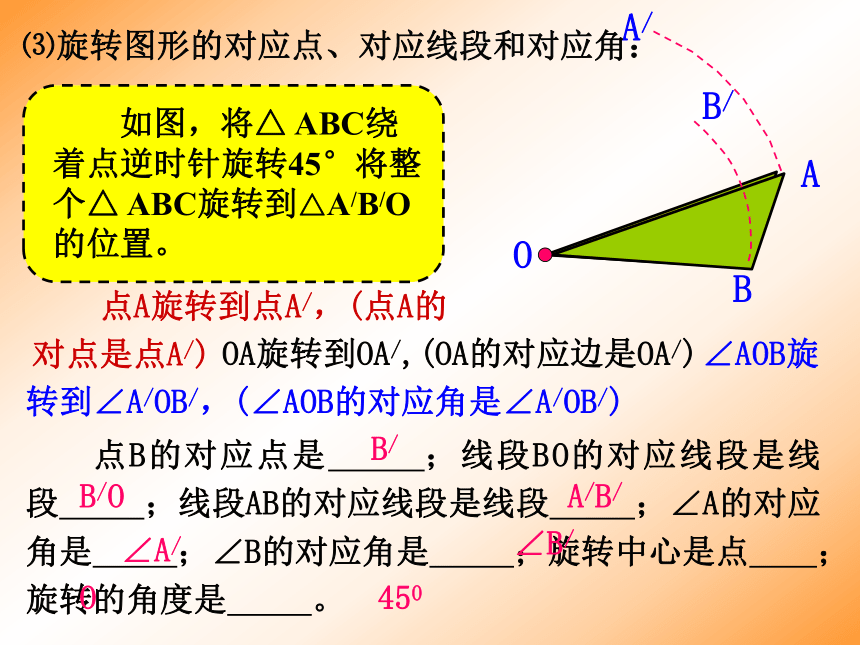
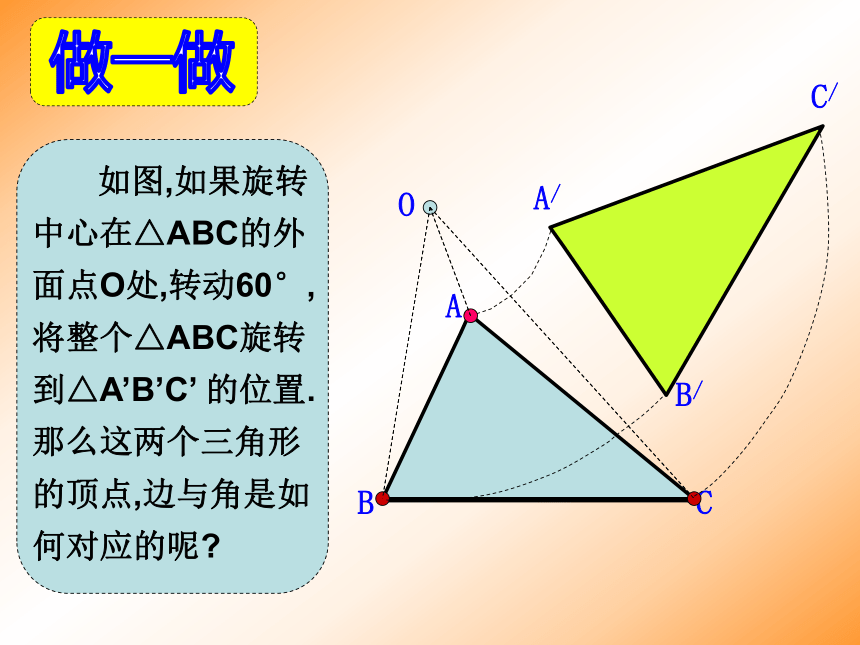
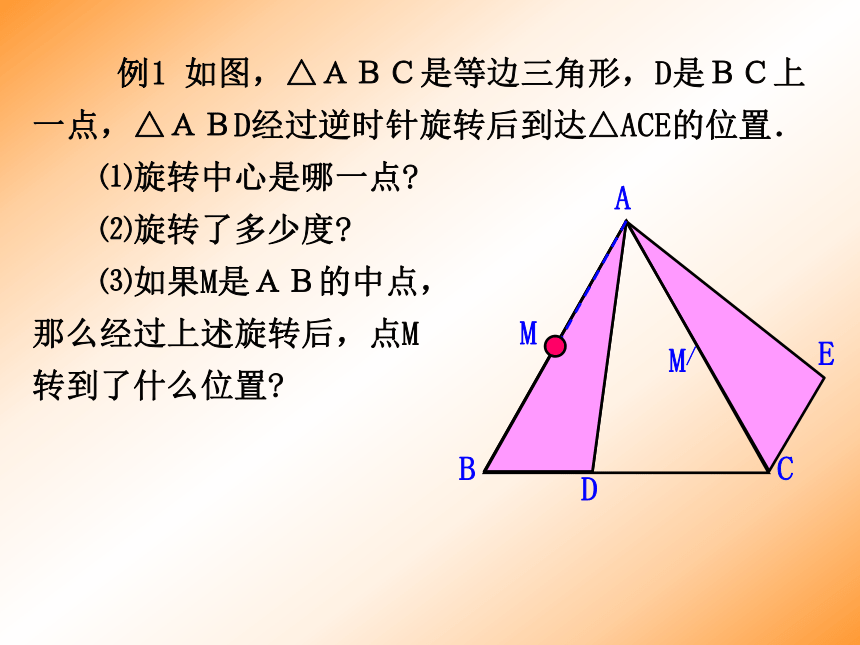
旋转方向 ∠AOB旋转到∠A/OB/,(∠AOB的对应角是∠A/OB/)ABO 点B的对应点是 ;线段BO的对应线段是线段 ;线段AB的对应线段是线段 ;∠A的对应角是 ;∠B的对应角是 ;旋转中心是点 ;旋转的角度是 。 点A旋转到点A/,(点A的对点是点A/)OA旋转到OA/,(OA的对应边是OA/)B/OB/A/B/∠A/∠B/O450 ⑶旋转图形的对应点、对应线段和对应角: 如图,如果旋转中心在△ABC的外面点O处,转动60°,将整个△ABC旋转到△A’B’C’ 的位置.那么这两个三角形的顶点,边与角是如何对应的呢?ABCA/B/C/O 点A的对应点是 ;点B的对应点是点 ;点C的对应点是点 。线段AB的对应线段是线段 ;线段BC的对应线段是线段 ;线段CA的对应线段是 。 ∠A的对应角是 ;∠B的对应角是 ;∠C的对应角是 。A/B/C/A/B/B/C/C/A/∠A/∠B/∠C/ 例1 如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如果M是AB的中点,
那么经过上述旋转后,点M
转到了什么位置?
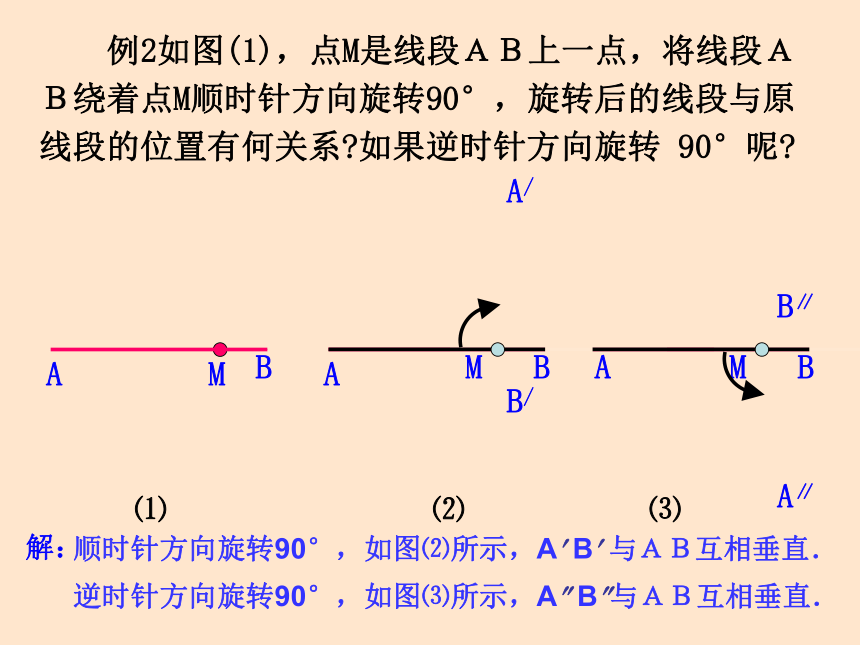
ABCDEMM/ 例2如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?A/MBA∥B/⑴⑵⑶AAMABMBB∥顺时针方向旋转90°,如图⑵所示,A? B? 与AB互相垂直.逆时针方向旋转90°,如图⑶所示,A? B?与AB互相垂直.解:今天你学到了什么?10.3旋转⑴1.图形的旋转 ⑵旋转三要素:⑴旋转的定义: ⑶旋转图形的对应点、对应线段和对应角:同学们,再见!2013.5.29制作:遂宁一中HDL华东师大版七年级下册《数学》10.3旋转(第2课时)10.3旋转⑴1.图形的旋转 ⑵旋转三要素:⑴旋转的定义: ⑶旋转图形的对应点、对应线段和对应角:ABOOA=OA/ 观察右图,你能发现有哪些
线段相等?有哪些角相等?OB=OB/AB=A/B/∠A=∠A/∠B=∠B/∠AOB=∠A/OB/ 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.⑴图形旋转的特征: ⑵画旋转图形: ACDOB700 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。解:如图,⑴连结OC、OD,量得旋转角∠COD=700。 把点B绕点O逆时针旋转700得点F;F700E⑵画旋转图形: ACDOB 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。解:如图,⑴连结OC、OD,量得旋转角∠COD=700。⑵把点A绕点O逆时针旋转700得点E;⑶连结DE、EF、FD。 ∴△ABC绕点O旋转后得到的三角形是△DEF。F700E⑵画旋转图形: ACDOB 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.可以看成连续两个箭头绕圆心旋转3次而生成,每次旋转90°1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.可以看成连续两个箭头绕圆心旋转3次而生成,每次旋转90°也可以看成中间间隔1个箭头绕圆心旋转1次而生成,每次旋转45°等等。3.画出△ABC绕点C逆时
针旋转90°后的图形. 2.如图,△ABC、△AEB都是等
腰三角形,∠CAD=∠EAB=900,
画出△ACE以点A为旋转中心,
逆时针旋转900后的三角形.今天你学到了什么?10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 同学们,再见!2013.5.29制作:遂宁一中HDL华东师大版七年级下册《数学》10.3旋转(第3课时)10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 观察下列图形在旋转过程中有什么特点? 定义:一个图形绕着一个定点,旋转一定的角度(小于3600)后能与自身重合,这样的图形称为旋转对称图形. 注意:⑴旋转是一种运动形式,而旋转对称图形是指一个图形; ⑵轴对称图形是将图形沿直线翻折后与自身重合,而旋转对称图形是绕某
一点旋转一定角度后与自身重合,它
们都是特殊图形。 ⑶旋转对称图形的旋转角不一定是唯一的。 把五角星先顺时针旋转720,再逆时针旋转720,你发现了什么? 再把五角星先顺时针旋转1440,再逆时针旋转1440,你发现了什么? 再把五角星先顺时针旋转2160,再逆时针旋转2160,你发现了什么? 再把五角星先顺时针旋转2880,再逆时针旋转2880,你发现了什么? 正五角星是旋转对称图形。并且顺时针或逆时针旋转某些相同角度时都能与自身重合。这种旋转对称图形可以不管旋转方向。 想一想:这个旋转对称图形有多少个旋转角,至少要旋转多少度? 例 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 解:左图是旋转对称图形,旋转中心是外框正方形对角
线的交点(如图中的点O),旋转角度是90°、1800、
2700,但它不是轴对称图形.O 例 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 解:右图也是旋转对称图形,旋转中心仍是外框正方形
对角线的交点(如图中的点M),旋转角度是180°,且
是轴对称图形.OM1.下列英文字母中属于旋转对称图形的是( )(A)(B)(C)(D)CSLK2.下列图形中,绕旋转中心旋转60°后能与自身重合的是( )(A)(B)(C)(D)3.如下四个图案都是旋转结称图形,其中有一个图案与其余三
个图形旋转的度数不同,它是( )(A)(B)(C)(D)4.下列说法中正确的是( )(A)是旋转对称图形,肯定不是轴对称图形;(B)是轴对称图形,肯定是旋转对称图形;(C)一些图形可能既是旋转对称图形,又是轴对称图形;(D)既不是旋转对称图形,又不是轴对称图形的图形不存在.正六边形、圆正三角形、正方形、线段、6.长方形的旋转中心是 ,
旋转 度与自身重合;正八边形旋
转_________ ___度能与自
身重合.对角线的交点180 如图,画△ABC和过点P的两条直线PQ、 PR.
画出△ABC关于PQ对称的三角形A′B′C′,
再画出△A′B′C′关于PR对称的三角形A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什
么关系吗?
ABCQRPA/C/B/A//B//C//C/A/ 把一个图形作两次轴对称变换,如果两条对称轴平行,那么相当于把这个图形作了一次平移变换.A//B/B//C// 如图,画△ABC和过点P的两条直线PQ、 PR.
画出△ABC关于PQ对称的三角形A′B′C′,
再画出△A′B′C′关于PR对称的三角形A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什
么关系吗?
ABCQRPA/C/B/A//B//C// 对此,你能总结出什么结论?结论: 把一个图形作两次轴对称变换,如果两条对称轴平行,那么相当于把这个图形作了一次平移变换. 把一个图形作两次轴对称变换,如果两条对称轴相交,那么相当于把这个图形绕对称轴的交点作了一次旋转变换.今天你学到了什么?10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 同学们,再见!2013.5.30 例 如图,E是正方形AB
CD内一点,∠AEB=1350,△AEB按顺时针绕点B旋转一个角度后成为△CBF。
求:⑴旋转角是多少度和∠AFC的度数;
⑵若BC=3cm,求EF的长。解:⑴∵△ABE绕点B旋转后成为△CBF∴∠ABC是旋转角, ∠BFC=∠BEA=1350(图形经过旋转对应角相等)∴∠ABC是旋转角, ∠BFC=∠BEA=1350(图形经过旋转对应角相等)∵四边形ABCD是正方形∴旋转角∠ABC=900。 ∵∠BEA=1350 ∴∠BEF=1800-∠BEA=1800-1350=450
旋转角度
旋转方向 ∠AOB旋转到∠A/OB/,(∠AOB的对应角是∠A/OB/)ABO 点B的对应点是 ;线段BO的对应线段是线段 ;线段AB的对应线段是线段 ;∠A的对应角是 ;∠B的对应角是 ;旋转中心是点 ;旋转的角度是 。 点A旋转到点A/,(点A的对点是点A/)OA旋转到OA/,(OA的对应边是OA/)B/OB/A/B/∠A/∠B/O450 ⑶旋转图形的对应点、对应线段和对应角: 如图,如果旋转中心在△ABC的外面点O处,转动60°,将整个△ABC旋转到△A’B’C’ 的位置.那么这两个三角形的顶点,边与角是如何对应的呢?ABCA/B/C/O 点A的对应点是 ;点B的对应点是点 ;点C的对应点是点 。线段AB的对应线段是线段 ;线段BC的对应线段是线段 ;线段CA的对应线段是 。 ∠A的对应角是 ;∠B的对应角是 ;∠C的对应角是 。A/B/C/A/B/B/C/C/A/∠A/∠B/∠C/ 例1 如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
⑴旋转中心是哪一点?
⑵旋转了多少度?
⑶如果M是AB的中点,
那么经过上述旋转后,点M
转到了什么位置?
ABCDEMM/ 例2如图(1),点M是线段AB上一点,将线段AB绕着点M顺时针方向旋转90°,旋转后的线段与原线段的位置有何关系?如果逆时针方向旋转 90°呢?A/MBA∥B/⑴⑵⑶AAMABMBB∥顺时针方向旋转90°,如图⑵所示,A? B? 与AB互相垂直.逆时针方向旋转90°,如图⑶所示,A? B?与AB互相垂直.解:今天你学到了什么?10.3旋转⑴1.图形的旋转 ⑵旋转三要素:⑴旋转的定义: ⑶旋转图形的对应点、对应线段和对应角:同学们,再见!2013.5.29制作:遂宁一中HDL华东师大版七年级下册《数学》10.3旋转(第2课时)10.3旋转⑴1.图形的旋转 ⑵旋转三要素:⑴旋转的定义: ⑶旋转图形的对应点、对应线段和对应角:ABOOA=OA/ 观察右图,你能发现有哪些
线段相等?有哪些角相等?OB=OB/AB=A/B/∠A=∠A/∠B=∠B/∠AOB=∠A/OB/ 图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状与大小都没有发生变化.⑴图形旋转的特征: ⑵画旋转图形: ACDOB700 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。解:如图,⑴连结OC、OD,量得旋转角∠COD=700。 把点B绕点O逆时针旋转700得点F;F700E⑵画旋转图形: ACDOB 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。解:如图,⑴连结OC、OD,量得旋转角∠COD=700。⑵把点A绕点O逆时针旋转700得点E;⑶连结DE、EF、FD。 ∴△ABC绕点O旋转后得到的三角形是△DEF。F700E⑵画旋转图形: ACDOB 例 如图△ABC绕点O旋转后,点
D和点C是对应点,作出△ABC旋转后的三角形。1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.可以看成连续两个箭头绕圆心旋转3次而生成,每次旋转90°1.确定图形中的旋转中心,指出这一图形可以看成是由哪个基本图形旋转而生成的,旋转几次,每一次旋转多少度.(不计颜色)解:旋转中心为圆心,本题图形由
8个箭头组成,答案不唯一。如:可以看成一个箭头绕圆心旋转7次而生成,每次旋转45°.可以看成连续两个箭头绕圆心旋转3次而生成,每次旋转90°也可以看成中间间隔1个箭头绕圆心旋转1次而生成,每次旋转45°等等。3.画出△ABC绕点C逆时
针旋转90°后的图形. 2.如图,△ABC、△AEB都是等
腰三角形,∠CAD=∠EAB=900,
画出△ACE以点A为旋转中心,
逆时针旋转900后的三角形.今天你学到了什么?10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 同学们,再见!2013.5.29制作:遂宁一中HDL华东师大版七年级下册《数学》10.3旋转(第3课时)10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 观察下列图形在旋转过程中有什么特点? 定义:一个图形绕着一个定点,旋转一定的角度(小于3600)后能与自身重合,这样的图形称为旋转对称图形. 注意:⑴旋转是一种运动形式,而旋转对称图形是指一个图形; ⑵轴对称图形是将图形沿直线翻折后与自身重合,而旋转对称图形是绕某
一点旋转一定角度后与自身重合,它
们都是特殊图形。 ⑶旋转对称图形的旋转角不一定是唯一的。 把五角星先顺时针旋转720,再逆时针旋转720,你发现了什么? 再把五角星先顺时针旋转1440,再逆时针旋转1440,你发现了什么? 再把五角星先顺时针旋转2160,再逆时针旋转2160,你发现了什么? 再把五角星先顺时针旋转2880,再逆时针旋转2880,你发现了什么? 正五角星是旋转对称图形。并且顺时针或逆时针旋转某些相同角度时都能与自身重合。这种旋转对称图形可以不管旋转方向。 想一想:这个旋转对称图形有多少个旋转角,至少要旋转多少度? 例 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 解:左图是旋转对称图形,旋转中心是外框正方形对角
线的交点(如图中的点O),旋转角度是90°、1800、
2700,但它不是轴对称图形.O 例 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 解:右图也是旋转对称图形,旋转中心仍是外框正方形
对角线的交点(如图中的点M),旋转角度是180°,且
是轴对称图形.OM1.下列英文字母中属于旋转对称图形的是( )(A)(B)(C)(D)CSLK2.下列图形中,绕旋转中心旋转60°后能与自身重合的是( )(A)(B)(C)(D)3.如下四个图案都是旋转结称图形,其中有一个图案与其余三
个图形旋转的度数不同,它是( )(A)(B)(C)(D)4.下列说法中正确的是( )(A)是旋转对称图形,肯定不是轴对称图形;(B)是轴对称图形,肯定是旋转对称图形;(C)一些图形可能既是旋转对称图形,又是轴对称图形;(D)既不是旋转对称图形,又不是轴对称图形的图形不存在.正六边形、圆正三角形、正方形、线段、6.长方形的旋转中心是 ,
旋转 度与自身重合;正八边形旋
转_________ ___度能与自
身重合.对角线的交点180 如图,画△ABC和过点P的两条直线PQ、 PR.
画出△ABC关于PQ对称的三角形A′B′C′,
再画出△A′B′C′关于PR对称的三角形A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什
么关系吗?
ABCQRPA/C/B/A//B//C//C/A/ 把一个图形作两次轴对称变换,如果两条对称轴平行,那么相当于把这个图形作了一次平移变换.A//B/B//C// 如图,画△ABC和过点P的两条直线PQ、 PR.
画出△ABC关于PQ对称的三角形A′B′C′,
再画出△A′B′C′关于PR对称的三角形A″B″C″.
观察△ABC和△A″B″C″,你能发现这两个三角形有什
么关系吗?
ABCQRPA/C/B/A//B//C// 对此,你能总结出什么结论?结论: 把一个图形作两次轴对称变换,如果两条对称轴平行,那么相当于把这个图形作了一次平移变换. 把一个图形作两次轴对称变换,如果两条对称轴相交,那么相当于把这个图形绕对称轴的交点作了一次旋转变换.今天你学到了什么?10.3旋转⑵2.旋转的特征⑴图形旋转的特征: ⑵画旋转图形: 同学们,再见!2013.5.30 例 如图,E是正方形AB
CD内一点,∠AEB=1350,△AEB按顺时针绕点B旋转一个角度后成为△CBF。
求:⑴旋转角是多少度和∠AFC的度数;
⑵若BC=3cm,求EF的长。解:⑴∵△ABE绕点B旋转后成为△CBF∴∠ABC是旋转角, ∠BFC=∠BEA=1350(图形经过旋转对应角相等)∴∠ABC是旋转角, ∠BFC=∠BEA=1350(图形经过旋转对应角相等)∵四边形ABCD是正方形∴旋转角∠ABC=900。 ∵∠BEA=1350 ∴∠BEF=1800-∠BEA=1800-1350=450
