19.2.2菱形复习课件
文档属性
| 名称 | 19.2.2菱形复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 781.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-28 21:56:58 | ||
图片预览


文档简介
课件30张PPT。 我的昨天,你可以鄙视;
我的今天,你不可轻视;
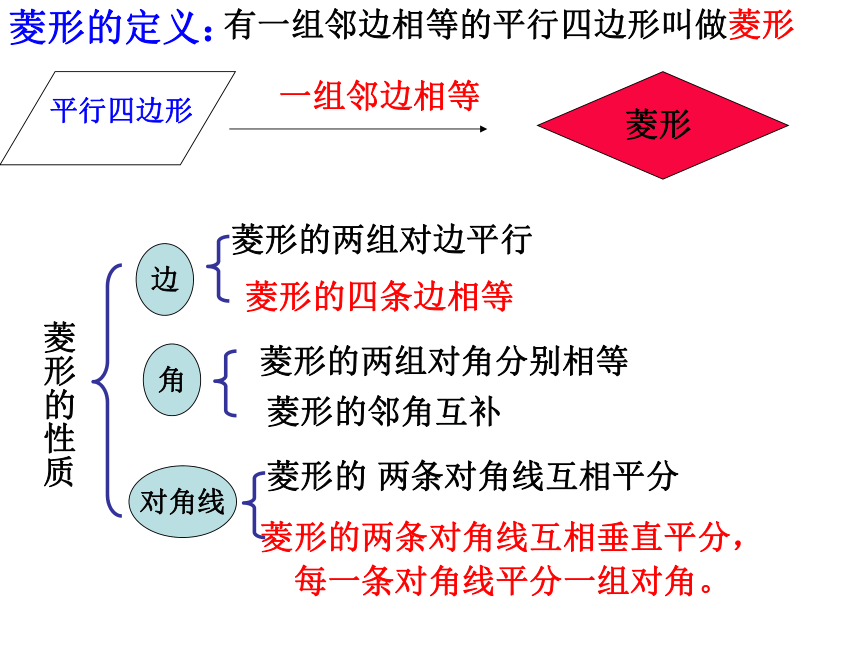
我的明天,你必须重视人的一生只有三天:昨天、今天、明天因为,我反思昨天、把握今天、描绘明天;因为,我自信、我努力。一组邻边相等有一组邻边相等的平行四边形叫做菱形边对角线角菱形的定义:菱形的性质菱形菱形的 两条对角线互相平分菱形的两组对边平行菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平分,
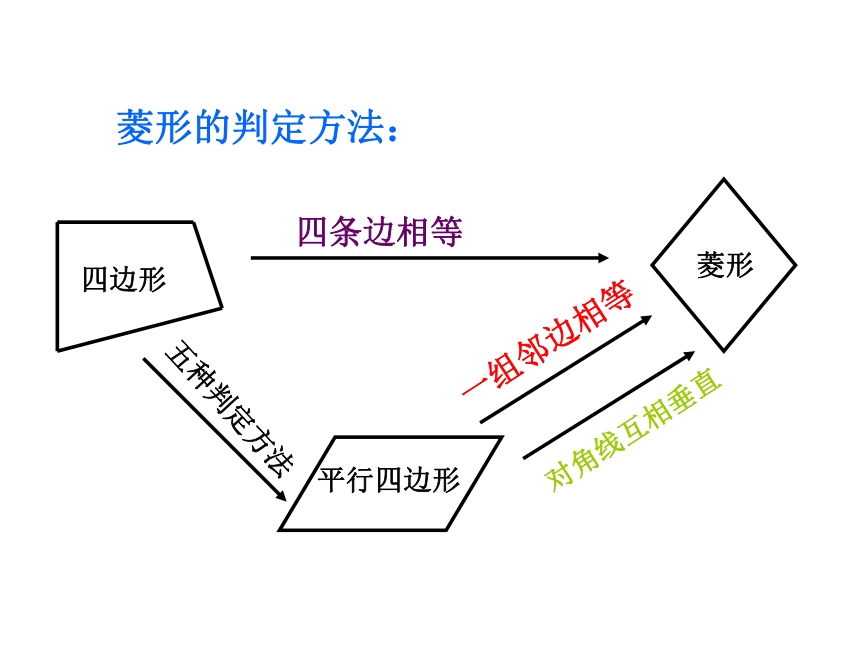
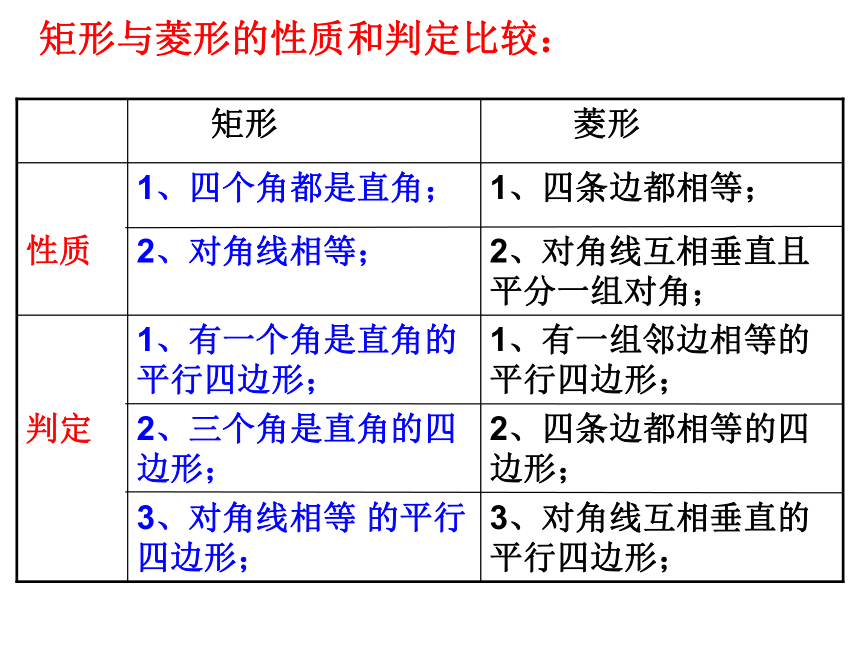
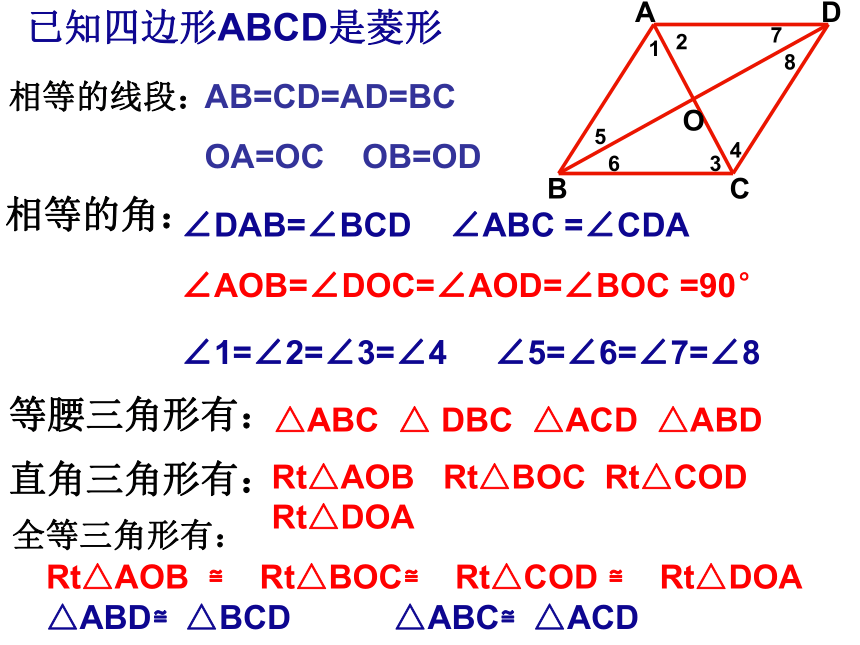
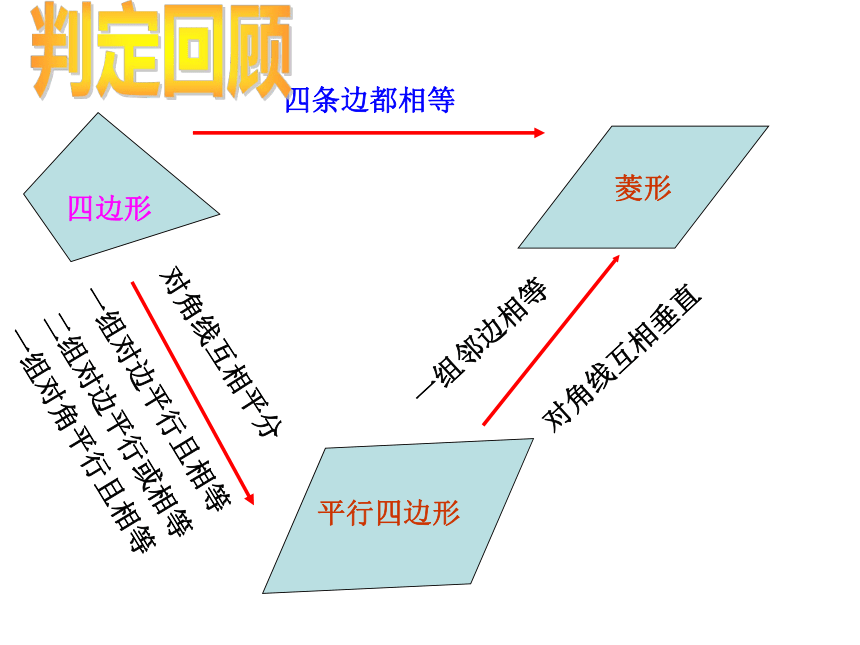
每一条对角线平分一组对角。一组邻边相等对角线互相垂直四条边相等五种判定方法四边形菱形的判定方法:3、对角线互相垂直的平行四边形;3、对角线相等 的平行四边形;2、四条边都相等的四边形;2、三个角是直角的四边形;判定1、有一组邻边相等的平行四边形;1、有一个角是直角的平行四边形;2、对角线互相垂直且平分一组对角;2、对角线相等;性质1、四条边都相等;1、四个角都是直角; 菱形 矩形矩形与菱形的性质和判定比较:相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678四条边都相等菱形一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等二组对边平行或相等判定回顾四边形平行四边形一组对角平行且相等1.叙述菱形的定义与性质.
2.菱形的两条对角线长分别是3和4,则周长和面积分别是___________、___________.
3.菱形周长为80,一对角线为20,则较小的角的度数为______、面积为_______.
4.菱形一边与两条对角线夹角的差是20°,那么菱形各角的度数分别为________.
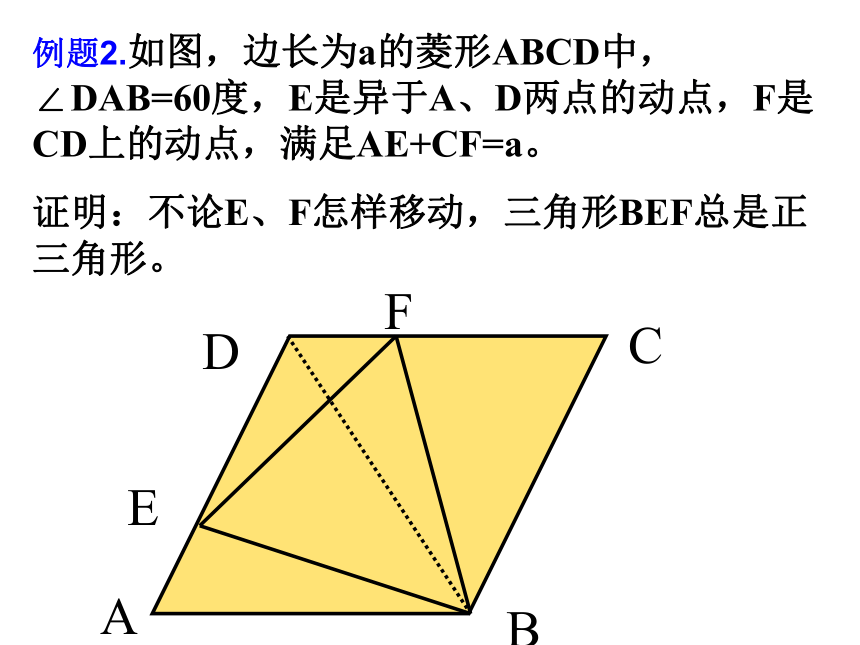
5.已知:菱形的周长为40cm,两条对角线长的比是3:4。求两对角线长分别是 。例1:(1)填空:例题2.如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
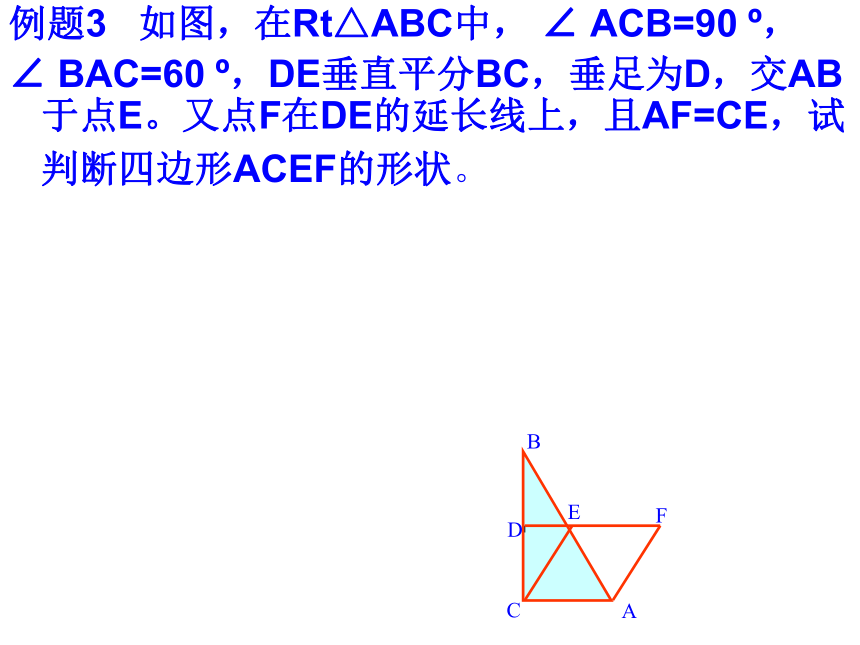
证明:不论E、F怎样移动,三角形BEF总是正三角形。ABCDEF例题3 如图,在Rt△ABC中, ∠ ACB=90 o,
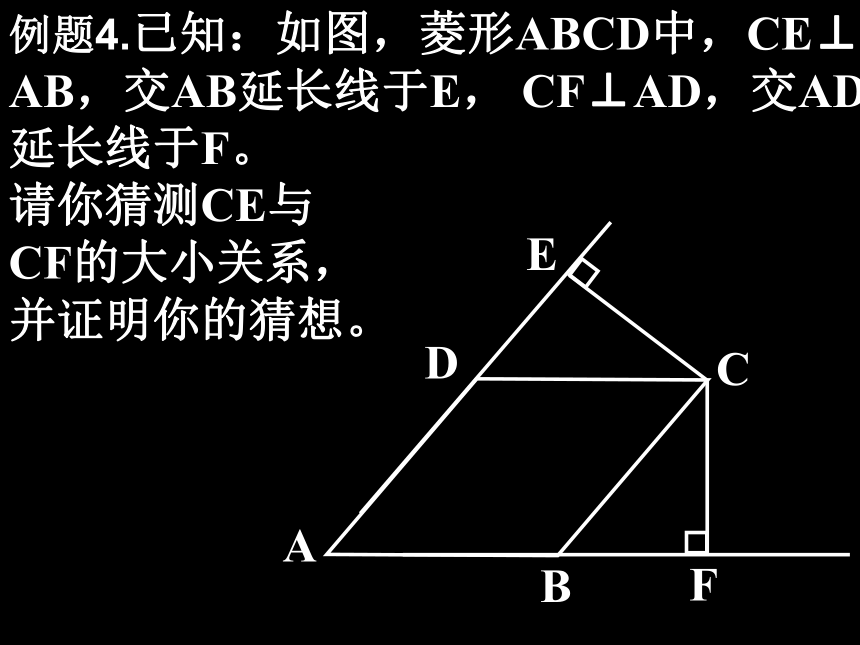
∠ BAC=60 o,DE垂直平分BC,垂足为D,交AB于点E。又点F在DE的延长线上,且AF=CE,试判断四边形ACEF的形状。 FEDCBA例题4.已知:如图,菱形ABCD中,CE⊥
AB,交AB延长线于E, CF⊥AD,交AD延长线于F。
请你猜测CE与
CF的大小关系,
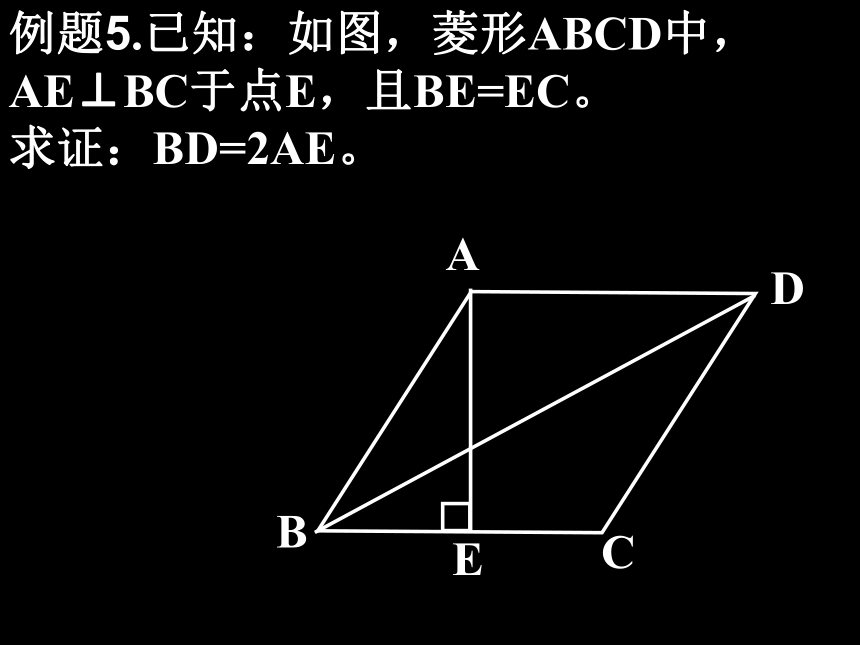
并证明你的猜想。例题5.已知:如图,菱形ABCD中,AE⊥BC于点E,且BE=EC。
求证:BD=2AE。例10、如图,已知在□ABCD中AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.例11。CD为Rt△ABC斜边AB上的高∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
例12:(1)、已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。1232、已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。 例13。已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形? (2)试证明你的猜想。 (3)? PO与CD有怎样的关系?
四边形PCOD是菱形。PO与CD互相垂直且平分已知,如图, ∠ ABC中, ∠ ACB= 900,BF平分∠ ABC,CD垂直于AB于D,和BF交于点G , GE ∥ CA.
求证:CE和FG互相垂直平分。例14、Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,
(1)求y与x之间的函数关系式?
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?ABCDMNP828ABCDMNP828第一种情形:解:(1)当0≤x≤2时,∵MC=xcm,∠PMN=450∴CE=xcm,GFEMNP8GFHT解:(2)当2<x≤6时,∵MC=x,MF=GF=2,∴CF=GD= x-2第二种情形:MNP8GFHT解:(3)当6<x≤8时,第三种情形:∴S重叠=S五边形GMCQH=S梯形GMNH-SΔQCNQ∵y= 0≤x≤22x-2,2<x≤66<x≤8(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?8则若2x-2 =8,则x=5,合题意,保留∴当x=5时,重叠部分的面积为RtΔPNN的面积的一半ABCDMNP828P第一种情形:PD解:(1)当0≤x≤2时,∴y=3OP,易证ΔPOD为一等边三角形,=3x第二种情形:PQMN解:(2)当2<x≤4时,y=3OP-OQ=3x-(x-2)=2x+2第三种情形:PQMN解:(3)当4<x≤6时,y=OC+BC+AQ+AP =4OA-OQ-BP=16-(x-2)-(8-x)=10第四种情形:PNMQ解:(4)当6<x≤8时,y=NQ+BN+QP=3QB-PB=3[4-2(x-6)]-(8-x)=40-5xy=3x,2x+2,10,40-5x,0≤x≤22<x≤44<x≤66<x≤8∴当4≤x≤6时,周长y是一个定值,定值为10例16。某中学有一块长为a米,宽为b米的矩形场地,计划在
该场地上修筑宽都为2米的两条互相垂直的道路,
余下的4块矩形小场地建成草坪.(如图)
(1)这两条道路面积的和为 m2
(2)如果 a ∶b=2∶1,并且4块草坪的面
积之和为312m2,则a= m,b= m.(3)在(2)的条件下,为进一步美化校园,根据实际情况,学校
决定对整个矩形场地作如下设计(要求同时符合下述两个
条件)
①在每块草坪上各修建一个面积尽可能大的菱形花圃
(花圃各边必须分别与所在草坪的对角线平行),并且其
中有两个花圃的面积之差为13m2.
②整个矩形场地(包括道路草坪花圃)为轴对称图形.
请你画出符合上述设计方案的一种草图,并求出每个
菱形花圃的面积再 见
我的今天,你不可轻视;
我的明天,你必须重视人的一生只有三天:昨天、今天、明天因为,我反思昨天、把握今天、描绘明天;因为,我自信、我努力。一组邻边相等有一组邻边相等的平行四边形叫做菱形边对角线角菱形的定义:菱形的性质菱形菱形的 两条对角线互相平分菱形的两组对边平行菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。一组邻边相等对角线互相垂直四条边相等五种判定方法四边形菱形的判定方法:3、对角线互相垂直的平行四边形;3、对角线相等 的平行四边形;2、四条边都相等的四边形;2、三个角是直角的四边形;判定1、有一组邻边相等的平行四边形;1、有一个角是直角的平行四边形;2、对角线互相垂直且平分一组对角;2、对角线相等;性质1、四条边都相等;1、四个角都是直角; 菱形 矩形矩形与菱形的性质和判定比较:相等的线段:相等的角:等腰三角形有:直角三角形有:全等三角形有:已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678四条边都相等菱形一组邻边相等对角线互相垂直对角线互相平分一组对边平行且相等二组对边平行或相等判定回顾四边形平行四边形一组对角平行且相等1.叙述菱形的定义与性质.
2.菱形的两条对角线长分别是3和4,则周长和面积分别是___________、___________.
3.菱形周长为80,一对角线为20,则较小的角的度数为______、面积为_______.
4.菱形一边与两条对角线夹角的差是20°,那么菱形各角的度数分别为________.
5.已知:菱形的周长为40cm,两条对角线长的比是3:4。求两对角线长分别是 。例1:(1)填空:例题2.如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。ABCDEF例题3 如图,在Rt△ABC中, ∠ ACB=90 o,
∠ BAC=60 o,DE垂直平分BC,垂足为D,交AB于点E。又点F在DE的延长线上,且AF=CE,试判断四边形ACEF的形状。 FEDCBA例题4.已知:如图,菱形ABCD中,CE⊥
AB,交AB延长线于E, CF⊥AD,交AD延长线于F。
请你猜测CE与
CF的大小关系,
并证明你的猜想。例题5.已知:如图,菱形ABCD中,AE⊥BC于点E,且BE=EC。
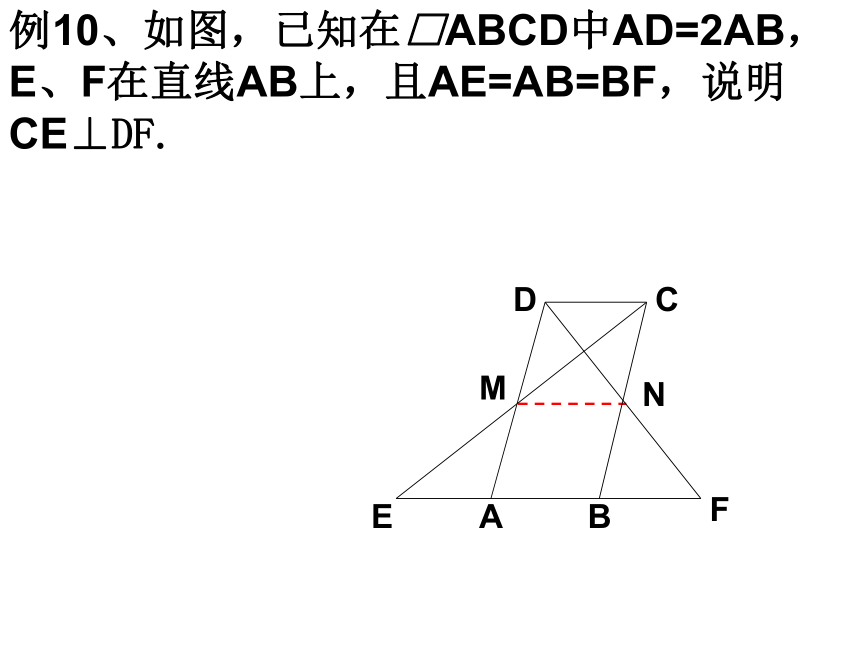
求证:BD=2AE。例10、如图,已知在□ABCD中AD=2AB,E、F在直线AB上,且AE=AB=BF,说明CE⊥DF.例11。CD为Rt△ABC斜边AB上的高∠BAC的平分线交CD于E,交BC于F,FG⊥AB于G.求证:四边形EGFC为菱形.
例12:(1)、已知: ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F 求证:四边形AFCE是菱形。1232、已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。 例13。已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形? (2)试证明你的猜想。 (3)? PO与CD有怎样的关系?
四边形PCOD是菱形。PO与CD互相垂直且平分已知,如图, ∠ ABC中, ∠ ACB= 900,BF平分∠ ABC,CD垂直于AB于D,和BF交于点G , GE ∥ CA.
求证:CE和FG互相垂直平分。例14、Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。令Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,
(1)求y与x之间的函数关系式?
(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?ABCDMNP828ABCDMNP828第一种情形:解:(1)当0≤x≤2时,∵MC=xcm,∠PMN=450∴CE=xcm,GFEMNP8GFHT解:(2)当2<x≤6时,∵MC=x,MF=GF=2,∴CF=GD= x-2第二种情形:MNP8GFHT解:(3)当6<x≤8时,第三种情形:∴S重叠=S五边形GMCQH=S梯形GMNH-SΔQCNQ∵y= 0≤x≤22x-2,2<x≤66<x≤8(2)若重叠部分的面积为等腰直角ΔPMN面积的一半,求x?8则若2x-2 =8,则x=5,合题意,保留∴当x=5时,重叠部分的面积为RtΔPNN的面积的一半ABCDMNP828P第一种情形:PD解:(1)当0≤x≤2时,∴y=3OP,易证ΔPOD为一等边三角形,=3x第二种情形:PQMN解:(2)当2<x≤4时,y=3OP-OQ=3x-(x-2)=2x+2第三种情形:PQMN解:(3)当4<x≤6时,y=OC+BC+AQ+AP =4OA-OQ-BP=16-(x-2)-(8-x)=10第四种情形:PNMQ解:(4)当6<x≤8时,y=NQ+BN+QP=3QB-PB=3[4-2(x-6)]-(8-x)=40-5xy=3x,2x+2,10,40-5x,0≤x≤22<x≤44<x≤66<x≤8∴当4≤x≤6时,周长y是一个定值,定值为10例16。某中学有一块长为a米,宽为b米的矩形场地,计划在
该场地上修筑宽都为2米的两条互相垂直的道路,
余下的4块矩形小场地建成草坪.(如图)
(1)这两条道路面积的和为 m2
(2)如果 a ∶b=2∶1,并且4块草坪的面
积之和为312m2,则a= m,b= m.(3)在(2)的条件下,为进一步美化校园,根据实际情况,学校
决定对整个矩形场地作如下设计(要求同时符合下述两个
条件)
①在每块草坪上各修建一个面积尽可能大的菱形花圃
(花圃各边必须分别与所在草坪的对角线平行),并且其
中有两个花圃的面积之差为13m2.
②整个矩形场地(包括道路草坪花圃)为轴对称图形.
请你画出符合上述设计方案的一种草图,并求出每个
菱形花圃的面积再 见
