01选择题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编(word含答案解析)
文档属性
| 名称 | 01选择题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 563.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:15:25 | ||
图片预览


文档简介
01选择题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编
一.并集及其运算(共1小题)
1.(2022 浙江)设集合A={1,2},B={2,4,6},则A∪B=( )
A.{2} B.{1,2} C.{2,4,6} D.{1,2,4,6}
二.交集及其运算(共2小题)
2.(2021 浙江)设集合A={x|x≥1},B={x|﹣1<x<2},则A∩B=( )
A.{x|x>﹣1} B.{x|x≥1} C.{x|﹣1<x<1} D.{x|1≤x<2}
3.(2020 浙江)已知集合P={x|1<x<4},Q={x|2<x<3},则P∩Q=( )
A.{x|1<x≤2} B.{x|2<x<3} C.{x|3≤x<4} D.{x|1<x<4}
三.充分条件、必要条件、充要条件(共2小题)
4.(2022 浙江)设x∈R,则“sinx=1”是“cosx=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.(2020 浙江)已知空间中不过同一点的三条直线l,m,n.则“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
四.命题的真假判断与应用(共1小题)
6.(2020 浙江)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:
①对于任意的x,y∈S,若x≠y,则xy∈T;
②对于任意的x,y∈T,若x<y,则∈S.下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
五.函数的图象与图象的变换(共2小题)
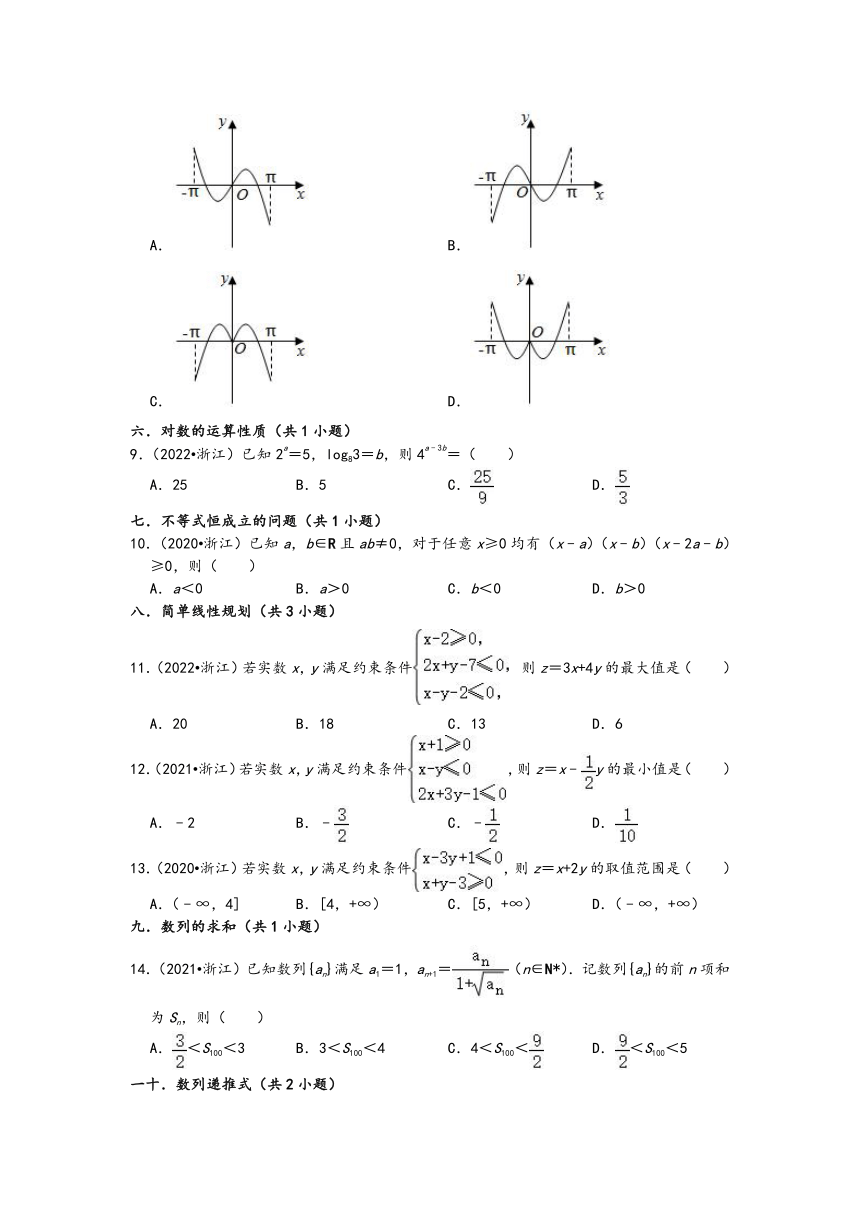
7.(2021 浙江)已知函数f(x)=x2+,g(x)=sinx,则图象为如图的函数可能是( )
A.y=f(x)+g(x)﹣ B.y=f(x)﹣g(x)﹣
C.y=f(x)g(x) D.y=
8.(2020 浙江)函数y=xcosx+sinx在区间[﹣π,π]上的图象可能是( )
A. B.
C. D.
六.对数的运算性质(共1小题)
9.(2022 浙江)已知2a=5,log83=b,则4a﹣3b=( )
A.25 B.5 C. D.
七.不等式恒成立的问题(共1小题)
10.(2020 浙江)已知a,b∈R且ab≠0,对于任意x≥0均有(x﹣a)(x﹣b)(x﹣2a﹣b)≥0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
八.简单线性规划(共3小题)
11.(2022 浙江)若实数x,y满足约束条件则z=3x+4y的最大值是( )
A.20 B.18 C.13 D.6
12.(2021 浙江)若实数x,y满足约束条件,则z=x﹣y的最小值是( )
A.﹣2 B.﹣ C.﹣ D.
13.(2020 浙江)若实数x,y满足约束条件,则z=x+2y的取值范围是( )
A.(﹣∞,4] B.[4,+∞) C.[5,+∞) D.(﹣∞,+∞)
九.数列的求和(共1小题)
14.(2021 浙江)已知数列{an}满足a1=1,an+1=(n∈N*).记数列{an}的前n项和为Sn,则( )
A.<S100<3 B.3<S100<4 C.4<S100< D.<S100<5
一十.数列递推式(共2小题)
15.(2022 浙江)已知数列{an}满足a1=1,an+1=an﹣an2(n∈N*),则( )
A.2<100a100< B.<100a100<3
C.3<100a100< D.<100a100<4
16.(2020 浙江)已知等差数列{an}的前n项和Sn,公差d≠0,且≤1.记b1=S2,bn+1=S2n+2﹣S2n,n∈N*,下列等式不可能成立的是( )
A.2a4=a2+a6 B.2b4=b2+b6 C.a42=a2a8 D.b42=b2b8
一十一.平面向量数量积的性质及其运算(共1小题)
17.(2021 浙江)已知非零向量,,,则“ = ”是“=”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
一十二.虚数单位i、复数(共2小题)
18.(2022 浙江)已知a,b∈R,a+3i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣3 B.a=﹣1,b=3 C.a=﹣1,b=﹣3 D.a=1,b=3
19.(2020 浙江)已知a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,则a=( )
A.1 B.﹣1 C.2 D.﹣2
一十三.复数的运算(共1小题)
20.(2021 浙江)已知a∈R,(1+ai)i=3+i(i为虚数单位),则a=( )
A.﹣1 B.1 C.﹣3 D.3
一十四.函数y=Asin(ωx+φ)的图象变换(共1小题)
21.(2022 浙江)为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
一十五.三角函数的最值(共1小题)
22.(2021 浙江)已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于的个数的最大值是( )
A.0 B.1 C.2 D.3
一十六.圆锥曲线的综合(共1小题)
23.(2020 浙江)已知点O(0,0),A(﹣2,0),B(2,0).设点P满足|PA|﹣|PB|=2,且P为函数y=3图象上的点,则|OP|=( )
A. B. C. D.
一十七.圆锥曲线的轨迹问题(共1小题)
24.(2021 浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R).若f(s﹣t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是( )
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
一十八.由三视图求面积、体积(共3小题)
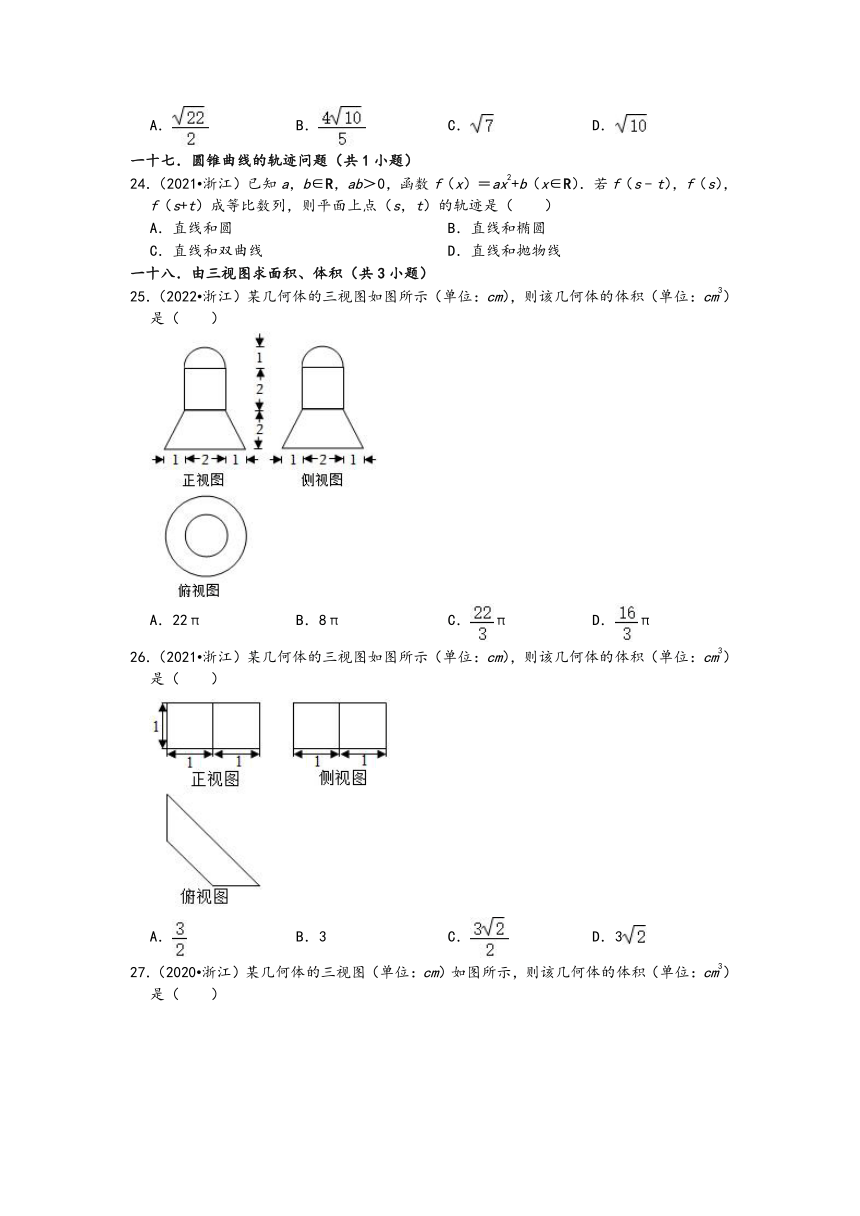
25.(2022 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.22π B.8π C.π D.π
26.(2021 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.3 C. D.3
27.(2020 浙江)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C.3 D.6
一十九.直线与平面平行(共1小题)
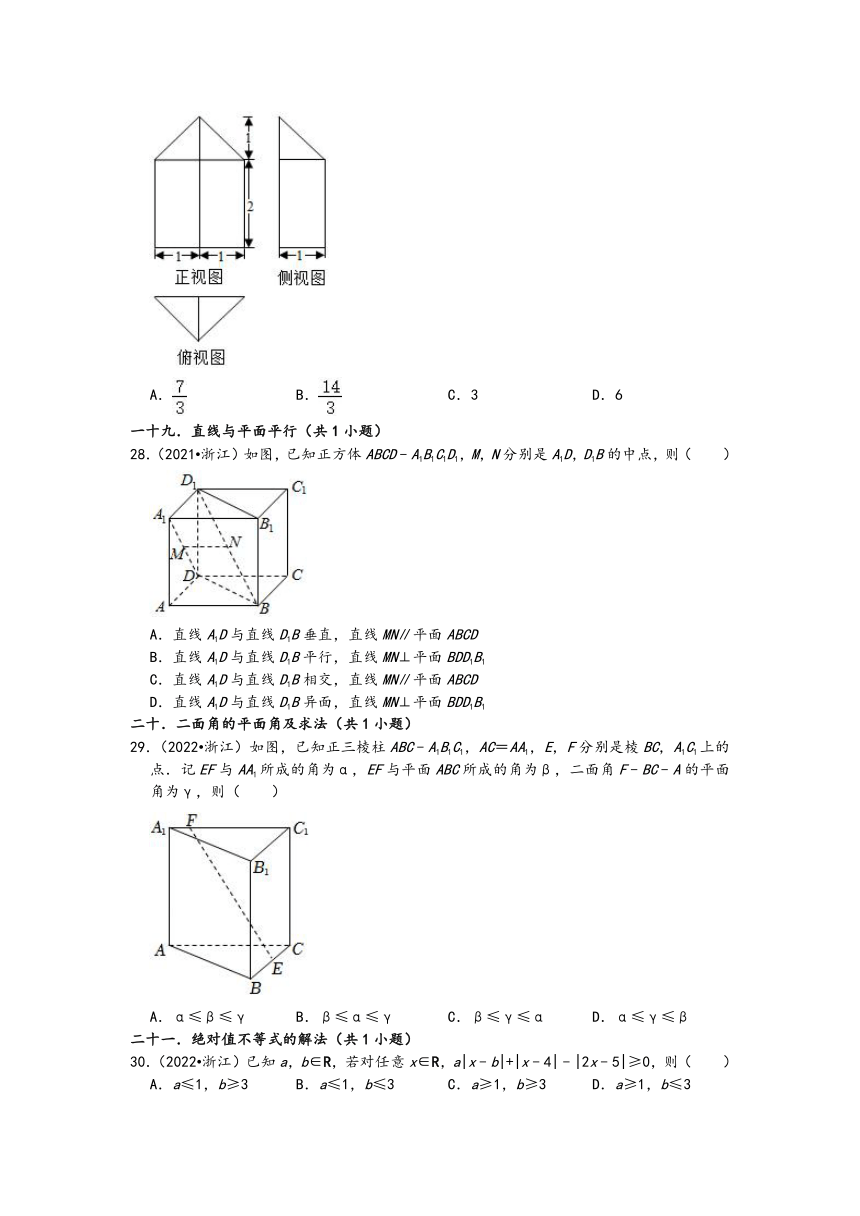
28.(2021 浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
二十.二面角的平面角及求法(共1小题)
29.(2022 浙江)如图,已知正三棱柱ABC﹣A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F﹣BC﹣A的平面角为γ,则( )
A.α≤β≤γ B.β≤α≤γ C.β≤γ≤α D.α≤γ≤β
二十一.绝对值不等式的解法(共1小题)
30.(2022 浙江)已知a,b∈R,若对任意x∈R,a|x﹣b|+|x﹣4|﹣|2x﹣5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3 C.a≥1,b≥3 D.a≥1,b≤3
参考答案与试题解析
一.并集及其运算(共1小题)
1.(2022 浙江)设集合A={1,2},B={2,4,6},则A∪B=( )
A.{2} B.{1,2} C.{2,4,6} D.{1,2,4,6}
【解析】解:∵A={1,2},B={2,4,6},
∴A∪B={1,2,4,6},
故选:D.
二.交集及其运算(共2小题)
2.(2021 浙江)设集合A={x|x≥1},B={x|﹣1<x<2},则A∩B=( )
A.{x|x>﹣1} B.{x|x≥1} C.{x|﹣1<x<1} D.{x|1≤x<2}
【解析】解:因为集合A={x|x≥1},B={x|﹣1<x<2},
所以A∩B={x|1≤x<2}.
故选:D.
3.(2020 浙江)已知集合P={x|1<x<4},Q={x|2<x<3},则P∩Q=( )
A.{x|1<x≤2} B.{x|2<x<3} C.{x|3≤x<4} D.{x|1<x<4}
【解析】解:集合P={x|1<x<4},Q={x|2<x<3},
则P∩Q={x|2<x<3}.
故选:B.
三.充分条件、必要条件、充要条件(共2小题)
4.(2022 浙江)设x∈R,则“sinx=1”是“cosx=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:∵sin2x+cos2x=1,
①当sinx=1时,则cosx=0,∴充分性成立,
②当cosx=0时,则sinx=±1,∴必要性不成立,
∴sinx=1是cosx=0的充分不必要条件,
故选:A.
5.(2020 浙江)已知空间中不过同一点的三条直线l,m,n.则“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:空间中不过同一点的三条直线m,n,l,若m,n,l在同一平面,则m,n,l相交或m,n,l有两个平行,另一直线与之相交,或三条直线两两平行.
而若“m,n,l两两相交”,则“m,n,l在同一平面”成立.
故m,n,l在同一平面”是“m,n,l两两相交”的必要不充分条件,
故选:B.
四.命题的真假判断与应用(共1小题)
6.(2020 浙江)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:
①对于任意的x,y∈S,若x≠y,则xy∈T;
②对于任意的x,y∈T,若x<y,则∈S.下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
【解析】解:取:S={1,2,4},则T={2,4,8},S∪T={1,2,4,8},4个元素,排除C.
S={2,4,8},则T={8,16,32},S∪T={2,4,8,16,32},5个元素,排除D;
S={2,4,8,16}则T={8,16,32,64,128},S∪T={2,4,8,16,32,64,128},7个元素,排除B;
故选:A.
五.函数的图象与图象的变换(共2小题)
7.(2021 浙江)已知函数f(x)=x2+,g(x)=sinx,则图象为如图的函数可能是( )
A.y=f(x)+g(x)﹣ B.y=f(x)﹣g(x)﹣
C.y=f(x)g(x) D.y=
【解析】解:由图可知,图象关于原点对称,则所求函数为奇函数,
因为f(x)=x2+为偶函数,g(x)=sinx为奇函数,
函数y=f(x)+g(x)﹣=x2+sinx为非奇非偶函数,故选项A错误;
函数y=f(x)﹣g(x)﹣=x2﹣sinx为非奇非偶函数,故选项B错误;
函数y=f(x)g(x)=(x2+)sinx,则y'=2xsinx+(x2+)cosx>0对x∈恒成立,
则函数y=f(x)g(x)在上单调递增,故选项C错误.
故选:D.
8.(2020 浙江)函数y=xcosx+sinx在区间[﹣π,π]上的图象可能是( )
A. B.
C. D.
【解析】解:y=f(x)=xcosx+sinx,
则f(﹣x)=﹣xcosx﹣sinx=﹣f(x),
∴f(x)为奇函数,函数图象关于原点对称,故排除C,D,
当x=π时,y=f(π)=πcosπ+sinπ=﹣π<0,故排除B,
故选:A.
六.对数的运算性质(共1小题)
9.(2022 浙江)已知2a=5,log83=b,则4a﹣3b=( )
A.25 B.5 C. D.
【解析】解:由2a=5,log83=b,
可得8b=23b=3,
则4a﹣3b====,
故选:C.
七.不等式恒成立的问题(共1小题)
10.(2020 浙江)已知a,b∈R且ab≠0,对于任意x≥0均有(x﹣a)(x﹣b)(x﹣2a﹣b)≥0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
【解析】解:设f(x)=(x﹣a)(x﹣b)(x﹣2a﹣b),可得f(x)的图象与x轴有三个交点,
即f(x)有三个零点a,b,2a+b且f(0)=﹣ab(2a+b),
由题意知,f(x)≥0在x≥0上恒成立,则ab(2a+b)≤0,a<0,b<0,
可得2a+b<0,ab(2a+b)≤0恒成立,排除B,D;
我们考虑零点重合的情况,即中间和右边的零点重合,左边的零点在负半轴上.
则有a=b或a=2a+b或b=b+2a三种情况,此时a=b<0显然成立;
若b=b+2a,则a=0不成立;
若a=2a+b,即a+b=0,可得b<0,a>0且a和2a+b都在正半轴上,符合题意,
综上b<0恒成立.
故选:C.
八.简单线性规划(共3小题)
11.(2022 浙江)若实数x,y满足约束条件则z=3x+4y的最大值是( )
A.20 B.18 C.13 D.6
【解析】解:实数x,y满足约束条件
则不等式组表示的平面区域为如图所示的阴影部分,
由已知可得A(2,3),
由图可知:当直线3x+4y﹣z=0过点A时,z取最大值,
则z=3x+4y的最大值是3×2+4×3=18,
故选:B.
12.(2021 浙江)若实数x,y满足约束条件,则z=x﹣y的最小值是( )
A.﹣2 B.﹣ C.﹣ D.
【解析】解:由约束条件作出可行域如图,
联立,解得A(﹣1,1),
化目标函数z=x﹣为y=2x﹣2z,由图可知,当直线y=2x﹣2z过A时,
直线在y轴上的截距最大,z有最小值为﹣1﹣.
故选:B.
13.(2020 浙江)若实数x,y满足约束条件,则z=x+2y的取值范围是( )
A.(﹣∞,4] B.[4,+∞) C.[5,+∞) D.(﹣∞,+∞)
【解析】解:画出实数x,y满足约束条件所示的平面区域,如图:由解得A(2,1),
将目标函数变形为﹣x+=y,
则表示直线在y轴上截距,截距越大,z越大,
当目标函数过点A(2,1)时,截距最小为z=2+2=4,随着目标函数向上移动截距越来越大,
故目标函数z=x+2y的取值范围是[4,+∞).
故选:B.
九.数列的求和(共1小题)
14.(2021 浙江)已知数列{an}满足a1=1,an+1=(n∈N*).记数列{an}的前n项和为Sn,则( )
A.<S100<3 B.3<S100<4 C.4<S100< D.<S100<5
【解析】解:因为 ,所以 ,所以 ,
,
∴,故 ,
由累加法可得当 n≥2 时,
,
又因为当 n=1 时, 也成立,所以,
所以 ,
∴,故,
由累乘法可得当 n≥2 时,,
所以 .
另解:设f(x)=,x>0,f′(x)=>0,可得f(x)在(0,+∞)递增,接下来运用待定系数法估计{an}的上下界,设an≤Mn=,则探索an+1也满足上界的条件.
an+1≤Mn+1 f(an)≤ f()≤
≤ λ ≥4.
在此条件下,有Sn≤=λ(﹣)<,
注意到a1=1,取λ=6,μ=1,从而M1=1,此时可得Sn<3.
故选:A.
一十.数列递推式(共2小题)
15.(2022 浙江)已知数列{an}满足a1=1,an+1=an﹣an2(n∈N*),则( )
A.2<100a100< B.<100a100<3
C.3<100a100< D.<100a100<4
【解析】解:∵an+1﹣an=﹣an2<0,
∴{an}为递减数列,
又,且an≠0,
∴,
又a1=1>0,则an>0,
∴,
∴,
∴,则,
∴;
由得,得,
累加可得,,
∴,
∴;
综上,.
故选:B.
16.(2020 浙江)已知等差数列{an}的前n项和Sn,公差d≠0,且≤1.记b1=S2,bn+1=S2n+2﹣S2n,n∈N*,下列等式不可能成立的是( )
A.2a4=a2+a6 B.2b4=b2+b6 C.a42=a2a8 D.b42=b2b8
【解析】解:
在等差数列{an}中,an=a1+(n﹣1)d,
∴a2=a1+d,a4=a1+3d,a8=a1+7d,
bn+1=S2n+2﹣S2n,
∴b2=S4﹣S2=a3+a4,
b4=S8﹣S6=a7+a8,
b6=S12﹣S10=a11+a12,
b8=S16﹣S14=a15+a16,
A.2a4=a2+a6,根据等差数列的性质可得A正确,
B.若2b4=b2+b6,则2(a7+a8)=a3+a4+a11+a12=(a3+a12)+(a4+a11),成立,B正确,
C.若a42=a2a8,则(a1+3d)2=(a1+d)(a1+7d),
即a12+6a1d+9d2=a12+8a1d+7d2,得a1d=d2,
∵d≠0,∴a1=d,符合≤1,C正确;
D.若b42=b2b8,则(a7+a8)2=(a3+a4)(a15+a16),
即4a12+52a1d+169d2=4a12+68a1d+145d2,得16a1d=24d2,
∵d≠0,∴2a1=3d,不符合≤1,D错误;
故选:D.
一十一.平面向量数量积的性质及其运算(共1小题)
17.(2021 浙江)已知非零向量,,,则“ = ”是“=”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:当且,则=0,但与不一定相等,
故不能推出,
则“ = ”是“=”的不充分条件;
由,可得,
则,即,
所以可以推出,
故“ = ”是“=”的必要条件.
综上所述,“ = ”是“=”的必要不充分条件.
故选:B.
一十二.虚数单位i、复数(共2小题)
18.(2022 浙江)已知a,b∈R,a+3i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣3 B.a=﹣1,b=3 C.a=﹣1,b=﹣3 D.a=1,b=3
【解析】解:∵a+3i=(b+i)i=﹣1+bi,a,b∈R,
∴a=﹣1,b=3,
故选:B.
19.(2020 浙江)已知a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,则a=( )
A.1 B.﹣1 C.2 D.﹣2
【解析】解:a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,
可得a﹣2=0,解得a=2.
故选:C.
一十三.复数的运算(共1小题)
20.(2021 浙江)已知a∈R,(1+ai)i=3+i(i为虚数单位),则a=( )
A.﹣1 B.1 C.﹣3 D.3
【解析】解:因为(1+ai)i=3+i,即﹣a+i=3+i,
由复数相等的定义可得,﹣a=3,即a=﹣3.
故选:C.
一十四.函数y=Asin(ωx+φ)的图象变换(共1小题)
21.(2022 浙江)为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】解:把y=2sin(3x+)图象上所有的点向右平移各单位可得y=2sin[3(x﹣)+]=2sin3x的图象.
故选:D.
一十五.三角函数的最值(共1小题)
22.(2021 浙江)已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于的个数的最大值是( )
A.0 B.1 C.2 D.3
【解析】解:由基本不等式可得:,,,
三式相加,可得:,
很明显sinαcosβ,sinβcosγ,sinγcosα 不可能均大于.
取α=30°,β=60°,γ=45°,
则,
则三式中大于 的个数的最大值为2,
故选:C.
一十六.圆锥曲线的综合(共1小题)
23.(2020 浙江)已知点O(0,0),A(﹣2,0),B(2,0).设点P满足|PA|﹣|PB|=2,且P为函数y=3图象上的点,则|OP|=( )
A. B. C. D.
【解析】解:点O (0,0),A(﹣2,0),B (2,0).设点P满足|PA|﹣|PB|=2,
可知P的轨迹是双曲线的右支上的点,
P为函数y=3图象上的点,即在第一象限的点,
联立两个方程,解得P(,),
所以|OP|==.
故选:D.
一十七.圆锥曲线的轨迹问题(共1小题)
24.(2021 浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R).若f(s﹣t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是( )
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
【解析】解:函数f(x)=ax2+b,因为f(s﹣t),f(s),f(s+t)成等比数列,
则f2(s)=f(s﹣t)f(s+t),即(as2+b)2=[a(s﹣t)2+b][a(s+t)2+b],
即a2s4+2abs2+b2=a2[(s﹣t)2(s+t)2]+ab(s﹣t)2+ab(s+t)2+b2,
整理可得a2t4﹣2a2s2t2+2abt2=0,
因为a≠0,故at4﹣2as2t2+2bt2=0,即t2(at2﹣2as2+2b)=0,
所以t=0或at2﹣2as2+2b=0,
当t=0时,点(s,t)的轨迹是直线;
当at2﹣2as2+2b=0,即,因为ab>0,故点(s,t)的轨迹是双曲线.
综上所述,平面上点(s,t)的轨迹是直线或双曲线.
故选:C.
一十八.由三视图求面积、体积(共3小题)
25.(2022 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.22π B.8π C.π D.π
【解析】解:由三视图可知几何体是上部为半球,中部是圆柱,下部是圆台,
所以几何体的体积为:+π×12×2+=π.
故选:C.
26.(2021 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.3 C. D.3
【解析】解:由三视图还原原几何体如图,
该几何体为直四棱柱,底面四边形ABCD为等腰梯形,
其中AB∥CD,由三视图可知,延长AD与BC后相交于一点,且AD⊥BC,
且AB=,CD=,AA1=1,等腰梯形的高为=,
则该几何体的体积V==.
故选:A.
27.(2020 浙江)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C.3 D.6
【解析】解:由题意可知几何体的直观图如图,下部是直三棱柱,底面是斜边长为2的等腰直角三角形,棱锥的高为2,上部是一个三棱锥,一个侧面与底面等腰直角三角形垂直,棱锥的高为1,
所以几何体的体积为:=.故选:A.
一十九.直线与平面平行(共1小题)
28.(2021 浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
【解析】解:连接AD1,如图:
由正方体可知A1D⊥AD1,A1D⊥AB,∴A1D⊥平面ABD1,
∴A1D⊥D1B,由题意知MN为△D1AB的中位线,∴MN∥AB,
又∵AB 平面ABCD,MN 平面ABCD,∴MN∥平面ABCD.∴A对;
由正方体可知A1D与平面BDD1相交于点D,D1B 平面BDD1,D D1B,
∴直线A1D与直线D1B是异面直线,∴B、C错;
∵MN∥AB,AB不与平面BDD1B1垂直,∴MN不与平面BDD1B1垂直,∴D错.
故选:A.
二十.二面角的平面角及求法(共1小题)
29.(2022 浙江)如图,已知正三棱柱ABC﹣A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F﹣BC﹣A的平面角为γ,则( )
A.α≤β≤γ B.β≤α≤γ C.β≤γ≤α D.α≤γ≤β
【解析】解:∵正三棱柱ABC﹣A1B1C1中,AC=AA1,
∴正三棱柱的所有棱长相等,设棱长为1,
如图,过F作FG⊥AC,垂足点为G,连接GE,则A1A∥FG,
∴EF与AA1所成的角为∠EFG=α,且tanα=,
又GE∈[0,1],∴tanα∈[0,1],
∴EF与平面ABC所成的角为∠FEG=β,且tanβ=∈[1,+∞),
∴tanβ≥tanα,...①,
再过G点作GH⊥BC,垂足点为H,连接HF,
又易知FG⊥底面ABC,BC 底面ABC,
∴BC⊥FG,又FG∩GH=G,∴BC⊥平面GHF,
∴二面角F﹣BC﹣A的平面角为∠GHF=γ,且tanγ=,又GH∈[0,1],
∴tanγ∈[1,+∞),∴tanγ≥tanα,...②,
又GE≥GH,∴tanβ≤tanγ,...③,
由①②③得tanα≤tanβ≤tanγ,又α,β,γ∈[0,),y=tanx在[0,)单调递增,
∴α≤β≤γ,
故选:A.
二十一.绝对值不等式的解法(共1小题)
30.(2022 浙江)已知a,b∈R,若对任意x∈R,a|x﹣b|+|x﹣4|﹣|2x﹣5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3 C.a≥1,b≥3 D.a≥1,b≤3
【解析】解:取x=4,则不等式为a|4﹣b|﹣3≥0,显然a≠0,且b≠4,
观察选项可知,只有选项D符合题意.
故选:D.
一.并集及其运算(共1小题)
1.(2022 浙江)设集合A={1,2},B={2,4,6},则A∪B=( )
A.{2} B.{1,2} C.{2,4,6} D.{1,2,4,6}
二.交集及其运算(共2小题)
2.(2021 浙江)设集合A={x|x≥1},B={x|﹣1<x<2},则A∩B=( )
A.{x|x>﹣1} B.{x|x≥1} C.{x|﹣1<x<1} D.{x|1≤x<2}
3.(2020 浙江)已知集合P={x|1<x<4},Q={x|2<x<3},则P∩Q=( )
A.{x|1<x≤2} B.{x|2<x<3} C.{x|3≤x<4} D.{x|1<x<4}
三.充分条件、必要条件、充要条件(共2小题)
4.(2022 浙江)设x∈R,则“sinx=1”是“cosx=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.(2020 浙江)已知空间中不过同一点的三条直线l,m,n.则“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
四.命题的真假判断与应用(共1小题)
6.(2020 浙江)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:
①对于任意的x,y∈S,若x≠y,则xy∈T;
②对于任意的x,y∈T,若x<y,则∈S.下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
五.函数的图象与图象的变换(共2小题)
7.(2021 浙江)已知函数f(x)=x2+,g(x)=sinx,则图象为如图的函数可能是( )
A.y=f(x)+g(x)﹣ B.y=f(x)﹣g(x)﹣
C.y=f(x)g(x) D.y=
8.(2020 浙江)函数y=xcosx+sinx在区间[﹣π,π]上的图象可能是( )
A. B.
C. D.
六.对数的运算性质(共1小题)
9.(2022 浙江)已知2a=5,log83=b,则4a﹣3b=( )
A.25 B.5 C. D.
七.不等式恒成立的问题(共1小题)
10.(2020 浙江)已知a,b∈R且ab≠0,对于任意x≥0均有(x﹣a)(x﹣b)(x﹣2a﹣b)≥0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
八.简单线性规划(共3小题)
11.(2022 浙江)若实数x,y满足约束条件则z=3x+4y的最大值是( )
A.20 B.18 C.13 D.6
12.(2021 浙江)若实数x,y满足约束条件,则z=x﹣y的最小值是( )
A.﹣2 B.﹣ C.﹣ D.
13.(2020 浙江)若实数x,y满足约束条件,则z=x+2y的取值范围是( )
A.(﹣∞,4] B.[4,+∞) C.[5,+∞) D.(﹣∞,+∞)
九.数列的求和(共1小题)
14.(2021 浙江)已知数列{an}满足a1=1,an+1=(n∈N*).记数列{an}的前n项和为Sn,则( )
A.<S100<3 B.3<S100<4 C.4<S100< D.<S100<5
一十.数列递推式(共2小题)
15.(2022 浙江)已知数列{an}满足a1=1,an+1=an﹣an2(n∈N*),则( )
A.2<100a100< B.<100a100<3
C.3<100a100< D.<100a100<4
16.(2020 浙江)已知等差数列{an}的前n项和Sn,公差d≠0,且≤1.记b1=S2,bn+1=S2n+2﹣S2n,n∈N*,下列等式不可能成立的是( )
A.2a4=a2+a6 B.2b4=b2+b6 C.a42=a2a8 D.b42=b2b8
一十一.平面向量数量积的性质及其运算(共1小题)
17.(2021 浙江)已知非零向量,,,则“ = ”是“=”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
一十二.虚数单位i、复数(共2小题)
18.(2022 浙江)已知a,b∈R,a+3i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣3 B.a=﹣1,b=3 C.a=﹣1,b=﹣3 D.a=1,b=3
19.(2020 浙江)已知a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,则a=( )
A.1 B.﹣1 C.2 D.﹣2
一十三.复数的运算(共1小题)
20.(2021 浙江)已知a∈R,(1+ai)i=3+i(i为虚数单位),则a=( )
A.﹣1 B.1 C.﹣3 D.3
一十四.函数y=Asin(ωx+φ)的图象变换(共1小题)
21.(2022 浙江)为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
一十五.三角函数的最值(共1小题)
22.(2021 浙江)已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于的个数的最大值是( )
A.0 B.1 C.2 D.3
一十六.圆锥曲线的综合(共1小题)
23.(2020 浙江)已知点O(0,0),A(﹣2,0),B(2,0).设点P满足|PA|﹣|PB|=2,且P为函数y=3图象上的点,则|OP|=( )
A. B. C. D.
一十七.圆锥曲线的轨迹问题(共1小题)
24.(2021 浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R).若f(s﹣t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是( )
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
一十八.由三视图求面积、体积(共3小题)
25.(2022 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.22π B.8π C.π D.π
26.(2021 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.3 C. D.3
27.(2020 浙江)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C.3 D.6
一十九.直线与平面平行(共1小题)
28.(2021 浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
二十.二面角的平面角及求法(共1小题)
29.(2022 浙江)如图,已知正三棱柱ABC﹣A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F﹣BC﹣A的平面角为γ,则( )
A.α≤β≤γ B.β≤α≤γ C.β≤γ≤α D.α≤γ≤β
二十一.绝对值不等式的解法(共1小题)
30.(2022 浙江)已知a,b∈R,若对任意x∈R,a|x﹣b|+|x﹣4|﹣|2x﹣5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3 C.a≥1,b≥3 D.a≥1,b≤3
参考答案与试题解析
一.并集及其运算(共1小题)
1.(2022 浙江)设集合A={1,2},B={2,4,6},则A∪B=( )
A.{2} B.{1,2} C.{2,4,6} D.{1,2,4,6}
【解析】解:∵A={1,2},B={2,4,6},
∴A∪B={1,2,4,6},
故选:D.
二.交集及其运算(共2小题)
2.(2021 浙江)设集合A={x|x≥1},B={x|﹣1<x<2},则A∩B=( )
A.{x|x>﹣1} B.{x|x≥1} C.{x|﹣1<x<1} D.{x|1≤x<2}
【解析】解:因为集合A={x|x≥1},B={x|﹣1<x<2},
所以A∩B={x|1≤x<2}.
故选:D.
3.(2020 浙江)已知集合P={x|1<x<4},Q={x|2<x<3},则P∩Q=( )
A.{x|1<x≤2} B.{x|2<x<3} C.{x|3≤x<4} D.{x|1<x<4}
【解析】解:集合P={x|1<x<4},Q={x|2<x<3},
则P∩Q={x|2<x<3}.
故选:B.
三.充分条件、必要条件、充要条件(共2小题)
4.(2022 浙江)设x∈R,则“sinx=1”是“cosx=0”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:∵sin2x+cos2x=1,
①当sinx=1时,则cosx=0,∴充分性成立,
②当cosx=0时,则sinx=±1,∴必要性不成立,
∴sinx=1是cosx=0的充分不必要条件,
故选:A.
5.(2020 浙江)已知空间中不过同一点的三条直线l,m,n.则“l,m,n共面”是“l,m,n两两相交”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:空间中不过同一点的三条直线m,n,l,若m,n,l在同一平面,则m,n,l相交或m,n,l有两个平行,另一直线与之相交,或三条直线两两平行.
而若“m,n,l两两相交”,则“m,n,l在同一平面”成立.
故m,n,l在同一平面”是“m,n,l两两相交”的必要不充分条件,
故选:B.
四.命题的真假判断与应用(共1小题)
6.(2020 浙江)设集合S,T,S N*,T N*,S,T中至少有2个元素,且S,T满足:
①对于任意的x,y∈S,若x≠y,则xy∈T;
②对于任意的x,y∈T,若x<y,则∈S.下列命题正确的是( )
A.若S有4个元素,则S∪T有7个元素
B.若S有4个元素,则S∪T有6个元素
C.若S有3个元素,则S∪T有5个元素
D.若S有3个元素,则S∪T有4个元素
【解析】解:取:S={1,2,4},则T={2,4,8},S∪T={1,2,4,8},4个元素,排除C.
S={2,4,8},则T={8,16,32},S∪T={2,4,8,16,32},5个元素,排除D;
S={2,4,8,16}则T={8,16,32,64,128},S∪T={2,4,8,16,32,64,128},7个元素,排除B;
故选:A.
五.函数的图象与图象的变换(共2小题)
7.(2021 浙江)已知函数f(x)=x2+,g(x)=sinx,则图象为如图的函数可能是( )
A.y=f(x)+g(x)﹣ B.y=f(x)﹣g(x)﹣
C.y=f(x)g(x) D.y=
【解析】解:由图可知,图象关于原点对称,则所求函数为奇函数,
因为f(x)=x2+为偶函数,g(x)=sinx为奇函数,
函数y=f(x)+g(x)﹣=x2+sinx为非奇非偶函数,故选项A错误;
函数y=f(x)﹣g(x)﹣=x2﹣sinx为非奇非偶函数,故选项B错误;
函数y=f(x)g(x)=(x2+)sinx,则y'=2xsinx+(x2+)cosx>0对x∈恒成立,
则函数y=f(x)g(x)在上单调递增,故选项C错误.
故选:D.
8.(2020 浙江)函数y=xcosx+sinx在区间[﹣π,π]上的图象可能是( )
A. B.
C. D.
【解析】解:y=f(x)=xcosx+sinx,
则f(﹣x)=﹣xcosx﹣sinx=﹣f(x),
∴f(x)为奇函数,函数图象关于原点对称,故排除C,D,
当x=π时,y=f(π)=πcosπ+sinπ=﹣π<0,故排除B,
故选:A.
六.对数的运算性质(共1小题)
9.(2022 浙江)已知2a=5,log83=b,则4a﹣3b=( )
A.25 B.5 C. D.
【解析】解:由2a=5,log83=b,
可得8b=23b=3,
则4a﹣3b====,
故选:C.
七.不等式恒成立的问题(共1小题)
10.(2020 浙江)已知a,b∈R且ab≠0,对于任意x≥0均有(x﹣a)(x﹣b)(x﹣2a﹣b)≥0,则( )
A.a<0 B.a>0 C.b<0 D.b>0
【解析】解:设f(x)=(x﹣a)(x﹣b)(x﹣2a﹣b),可得f(x)的图象与x轴有三个交点,
即f(x)有三个零点a,b,2a+b且f(0)=﹣ab(2a+b),
由题意知,f(x)≥0在x≥0上恒成立,则ab(2a+b)≤0,a<0,b<0,
可得2a+b<0,ab(2a+b)≤0恒成立,排除B,D;
我们考虑零点重合的情况,即中间和右边的零点重合,左边的零点在负半轴上.
则有a=b或a=2a+b或b=b+2a三种情况,此时a=b<0显然成立;
若b=b+2a,则a=0不成立;
若a=2a+b,即a+b=0,可得b<0,a>0且a和2a+b都在正半轴上,符合题意,
综上b<0恒成立.
故选:C.
八.简单线性规划(共3小题)
11.(2022 浙江)若实数x,y满足约束条件则z=3x+4y的最大值是( )
A.20 B.18 C.13 D.6
【解析】解:实数x,y满足约束条件
则不等式组表示的平面区域为如图所示的阴影部分,
由已知可得A(2,3),
由图可知:当直线3x+4y﹣z=0过点A时,z取最大值,
则z=3x+4y的最大值是3×2+4×3=18,
故选:B.
12.(2021 浙江)若实数x,y满足约束条件,则z=x﹣y的最小值是( )
A.﹣2 B.﹣ C.﹣ D.
【解析】解:由约束条件作出可行域如图,
联立,解得A(﹣1,1),
化目标函数z=x﹣为y=2x﹣2z,由图可知,当直线y=2x﹣2z过A时,
直线在y轴上的截距最大,z有最小值为﹣1﹣.
故选:B.
13.(2020 浙江)若实数x,y满足约束条件,则z=x+2y的取值范围是( )
A.(﹣∞,4] B.[4,+∞) C.[5,+∞) D.(﹣∞,+∞)
【解析】解:画出实数x,y满足约束条件所示的平面区域,如图:由解得A(2,1),
将目标函数变形为﹣x+=y,
则表示直线在y轴上截距,截距越大,z越大,
当目标函数过点A(2,1)时,截距最小为z=2+2=4,随着目标函数向上移动截距越来越大,
故目标函数z=x+2y的取值范围是[4,+∞).
故选:B.
九.数列的求和(共1小题)
14.(2021 浙江)已知数列{an}满足a1=1,an+1=(n∈N*).记数列{an}的前n项和为Sn,则( )
A.<S100<3 B.3<S100<4 C.4<S100< D.<S100<5
【解析】解:因为 ,所以 ,所以 ,
,
∴,故 ,
由累加法可得当 n≥2 时,
,
又因为当 n=1 时, 也成立,所以,
所以 ,
∴,故,
由累乘法可得当 n≥2 时,,
所以 .
另解:设f(x)=,x>0,f′(x)=>0,可得f(x)在(0,+∞)递增,接下来运用待定系数法估计{an}的上下界,设an≤Mn=,则探索an+1也满足上界的条件.
an+1≤Mn+1 f(an)≤ f()≤
≤ λ ≥4.
在此条件下,有Sn≤=λ(﹣)<,
注意到a1=1,取λ=6,μ=1,从而M1=1,此时可得Sn<3.
故选:A.
一十.数列递推式(共2小题)
15.(2022 浙江)已知数列{an}满足a1=1,an+1=an﹣an2(n∈N*),则( )
A.2<100a100< B.<100a100<3
C.3<100a100< D.<100a100<4
【解析】解:∵an+1﹣an=﹣an2<0,
∴{an}为递减数列,
又,且an≠0,
∴,
又a1=1>0,则an>0,
∴,
∴,
∴,则,
∴;
由得,得,
累加可得,,
∴,
∴;
综上,.
故选:B.
16.(2020 浙江)已知等差数列{an}的前n项和Sn,公差d≠0,且≤1.记b1=S2,bn+1=S2n+2﹣S2n,n∈N*,下列等式不可能成立的是( )
A.2a4=a2+a6 B.2b4=b2+b6 C.a42=a2a8 D.b42=b2b8
【解析】解:
在等差数列{an}中,an=a1+(n﹣1)d,
∴a2=a1+d,a4=a1+3d,a8=a1+7d,
bn+1=S2n+2﹣S2n,
∴b2=S4﹣S2=a3+a4,
b4=S8﹣S6=a7+a8,
b6=S12﹣S10=a11+a12,
b8=S16﹣S14=a15+a16,
A.2a4=a2+a6,根据等差数列的性质可得A正确,
B.若2b4=b2+b6,则2(a7+a8)=a3+a4+a11+a12=(a3+a12)+(a4+a11),成立,B正确,
C.若a42=a2a8,则(a1+3d)2=(a1+d)(a1+7d),
即a12+6a1d+9d2=a12+8a1d+7d2,得a1d=d2,
∵d≠0,∴a1=d,符合≤1,C正确;
D.若b42=b2b8,则(a7+a8)2=(a3+a4)(a15+a16),
即4a12+52a1d+169d2=4a12+68a1d+145d2,得16a1d=24d2,
∵d≠0,∴2a1=3d,不符合≤1,D错误;
故选:D.
一十一.平面向量数量积的性质及其运算(共1小题)
17.(2021 浙江)已知非零向量,,,则“ = ”是“=”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】解:当且,则=0,但与不一定相等,
故不能推出,
则“ = ”是“=”的不充分条件;
由,可得,
则,即,
所以可以推出,
故“ = ”是“=”的必要条件.
综上所述,“ = ”是“=”的必要不充分条件.
故选:B.
一十二.虚数单位i、复数(共2小题)
18.(2022 浙江)已知a,b∈R,a+3i=(b+i)i(i为虚数单位),则( )
A.a=1,b=﹣3 B.a=﹣1,b=3 C.a=﹣1,b=﹣3 D.a=1,b=3
【解析】解:∵a+3i=(b+i)i=﹣1+bi,a,b∈R,
∴a=﹣1,b=3,
故选:B.
19.(2020 浙江)已知a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,则a=( )
A.1 B.﹣1 C.2 D.﹣2
【解析】解:a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,
可得a﹣2=0,解得a=2.
故选:C.
一十三.复数的运算(共1小题)
20.(2021 浙江)已知a∈R,(1+ai)i=3+i(i为虚数单位),则a=( )
A.﹣1 B.1 C.﹣3 D.3
【解析】解:因为(1+ai)i=3+i,即﹣a+i=3+i,
由复数相等的定义可得,﹣a=3,即a=﹣3.
故选:C.
一十四.函数y=Asin(ωx+φ)的图象变换(共1小题)
21.(2022 浙江)为了得到函数y=2sin3x的图象,只要把函数y=2sin(3x+)图象上所有的点( )
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
【解析】解:把y=2sin(3x+)图象上所有的点向右平移各单位可得y=2sin[3(x﹣)+]=2sin3x的图象.
故选:D.
一十五.三角函数的最值(共1小题)
22.(2021 浙江)已知α,β,γ是互不相同的锐角,则在sinαcosβ,sinβcosγ,sinγcosα三个值中,大于的个数的最大值是( )
A.0 B.1 C.2 D.3
【解析】解:由基本不等式可得:,,,
三式相加,可得:,
很明显sinαcosβ,sinβcosγ,sinγcosα 不可能均大于.
取α=30°,β=60°,γ=45°,
则,
则三式中大于 的个数的最大值为2,
故选:C.
一十六.圆锥曲线的综合(共1小题)
23.(2020 浙江)已知点O(0,0),A(﹣2,0),B(2,0).设点P满足|PA|﹣|PB|=2,且P为函数y=3图象上的点,则|OP|=( )
A. B. C. D.
【解析】解:点O (0,0),A(﹣2,0),B (2,0).设点P满足|PA|﹣|PB|=2,
可知P的轨迹是双曲线的右支上的点,
P为函数y=3图象上的点,即在第一象限的点,
联立两个方程,解得P(,),
所以|OP|==.
故选:D.
一十七.圆锥曲线的轨迹问题(共1小题)
24.(2021 浙江)已知a,b∈R,ab>0,函数f(x)=ax2+b(x∈R).若f(s﹣t),f(s),f(s+t)成等比数列,则平面上点(s,t)的轨迹是( )
A.直线和圆 B.直线和椭圆
C.直线和双曲线 D.直线和抛物线
【解析】解:函数f(x)=ax2+b,因为f(s﹣t),f(s),f(s+t)成等比数列,
则f2(s)=f(s﹣t)f(s+t),即(as2+b)2=[a(s﹣t)2+b][a(s+t)2+b],
即a2s4+2abs2+b2=a2[(s﹣t)2(s+t)2]+ab(s﹣t)2+ab(s+t)2+b2,
整理可得a2t4﹣2a2s2t2+2abt2=0,
因为a≠0,故at4﹣2as2t2+2bt2=0,即t2(at2﹣2as2+2b)=0,
所以t=0或at2﹣2as2+2b=0,
当t=0时,点(s,t)的轨迹是直线;
当at2﹣2as2+2b=0,即,因为ab>0,故点(s,t)的轨迹是双曲线.
综上所述,平面上点(s,t)的轨迹是直线或双曲线.
故选:C.
一十八.由三视图求面积、体积(共3小题)
25.(2022 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.22π B.8π C.π D.π
【解析】解:由三视图可知几何体是上部为半球,中部是圆柱,下部是圆台,
所以几何体的体积为:+π×12×2+=π.
故选:C.
26.(2021 浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A. B.3 C. D.3
【解析】解:由三视图还原原几何体如图,
该几何体为直四棱柱,底面四边形ABCD为等腰梯形,
其中AB∥CD,由三视图可知,延长AD与BC后相交于一点,且AD⊥BC,
且AB=,CD=,AA1=1,等腰梯形的高为=,
则该几何体的体积V==.
故选:A.
27.(2020 浙江)某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是( )
A. B. C.3 D.6
【解析】解:由题意可知几何体的直观图如图,下部是直三棱柱,底面是斜边长为2的等腰直角三角形,棱锥的高为2,上部是一个三棱锥,一个侧面与底面等腰直角三角形垂直,棱锥的高为1,
所以几何体的体积为:=.故选:A.
一十九.直线与平面平行(共1小题)
28.(2021 浙江)如图,已知正方体ABCD﹣A1B1C1D1,M,N分别是A1D,D1B的中点,则( )
A.直线A1D与直线D1B垂直,直线MN∥平面ABCD
B.直线A1D与直线D1B平行,直线MN⊥平面BDD1B1
C.直线A1D与直线D1B相交,直线MN∥平面ABCD
D.直线A1D与直线D1B异面,直线MN⊥平面BDD1B1
【解析】解:连接AD1,如图:
由正方体可知A1D⊥AD1,A1D⊥AB,∴A1D⊥平面ABD1,
∴A1D⊥D1B,由题意知MN为△D1AB的中位线,∴MN∥AB,
又∵AB 平面ABCD,MN 平面ABCD,∴MN∥平面ABCD.∴A对;
由正方体可知A1D与平面BDD1相交于点D,D1B 平面BDD1,D D1B,
∴直线A1D与直线D1B是异面直线,∴B、C错;
∵MN∥AB,AB不与平面BDD1B1垂直,∴MN不与平面BDD1B1垂直,∴D错.
故选:A.
二十.二面角的平面角及求法(共1小题)
29.(2022 浙江)如图,已知正三棱柱ABC﹣A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F﹣BC﹣A的平面角为γ,则( )
A.α≤β≤γ B.β≤α≤γ C.β≤γ≤α D.α≤γ≤β
【解析】解:∵正三棱柱ABC﹣A1B1C1中,AC=AA1,
∴正三棱柱的所有棱长相等,设棱长为1,
如图,过F作FG⊥AC,垂足点为G,连接GE,则A1A∥FG,
∴EF与AA1所成的角为∠EFG=α,且tanα=,
又GE∈[0,1],∴tanα∈[0,1],
∴EF与平面ABC所成的角为∠FEG=β,且tanβ=∈[1,+∞),
∴tanβ≥tanα,...①,
再过G点作GH⊥BC,垂足点为H,连接HF,
又易知FG⊥底面ABC,BC 底面ABC,
∴BC⊥FG,又FG∩GH=G,∴BC⊥平面GHF,
∴二面角F﹣BC﹣A的平面角为∠GHF=γ,且tanγ=,又GH∈[0,1],
∴tanγ∈[1,+∞),∴tanγ≥tanα,...②,
又GE≥GH,∴tanβ≤tanγ,...③,
由①②③得tanα≤tanβ≤tanγ,又α,β,γ∈[0,),y=tanx在[0,)单调递增,
∴α≤β≤γ,
故选:A.
二十一.绝对值不等式的解法(共1小题)
30.(2022 浙江)已知a,b∈R,若对任意x∈R,a|x﹣b|+|x﹣4|﹣|2x﹣5|≥0,则( )
A.a≤1,b≥3 B.a≤1,b≤3 C.a≥1,b≥3 D.a≥1,b≤3
【解析】解:取x=4,则不等式为a|4﹣b|﹣3≥0,显然a≠0,且b≠4,
观察选项可知,只有选项D符合题意.
故选:D.
同课章节目录
