03解答题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编(word含答案解析)
文档属性
| 名称 | 03解答题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 806.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:16:39 | ||
图片预览



文档简介
03解答题知识点分类-浙江省三年(2020-2022)高考数学真题分类汇编
一.利用导数研究函数的单调性(共2小题)
1.(2022 浙江)设函数f(x)=+lnx(x>0).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)已知a,b∈R,曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:
(ⅰ)若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)若0<a<e,x1<x2<x3,则+<+<﹣.
(注:e=2.71828…是自然对数的底数)
2.(2021 浙江)设a,b为实数,且a>1,函数f(x)=ax﹣bx+e2(x∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围;
(Ⅲ)当a=e时,证明:对任意b>e4,函数f(x)有两个不同的零点x1,x2,满足x2>x1+.
(注:e=2.71828 是自然对数的底数)
二.利用导数研究函数的最值(共1小题)
3.(2020 浙江)已知1<a≤2,函数f(x)=ex﹣x﹣a,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数y=f(x)在(0,+∞)上有唯一零点;
(Ⅱ)记x0为函数y=f(x)在(0,+∞)上的零点,证明:
(ⅰ)≤x0≤;
(ⅱ)x0f(e)≥(e﹣1)(a﹣1)a.
三.数列的求和(共1小题)
4.(2020 浙江)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1﹣an,cn+1=cn(n∈N*).
(Ⅰ)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(Ⅱ)若{bn}为等差数列,公差d>0,证明:c1+c2+c3+…+cn<1+,n∈N*.
四.数列递推式(共1小题)
5.(2021 浙江)已知数列{an}的前n项和为Sn,a1=﹣,且4Sn+1=3Sn﹣9(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足3bn+(n﹣4)an=0(n∈N*),记{bn}的前n项和为Tn,若Tn≤λbn对任意n∈N*恒成立,
求实数λ的取值范围.
五.等差数列与等比数列的综合(共1小题)
6.(2022 浙江)已知等差数列{an}的首项a1=﹣1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(Ⅰ)若S4﹣2a2a3+6=0,求Sn;
(Ⅱ)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
六.三角函数中的恒等变换应用(共1小题)
7.(2021 浙江)设函数f(x)=sinx+cosx(x∈R).
(Ⅰ)求函数y=[f(x+)]2的最小正周期;
(Ⅱ)求函数y=f(x)f(x﹣)在[0,]上的最大值.
七.正弦定理(共1小题)
8.(2020 浙江)在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知2bsinA﹣a=0.
(Ⅰ)求角B的大小;
(Ⅱ)求cosA+cosB+cosC的取值范围.
八.三角形中的几何计算(共1小题)
9.(2022 浙江)在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
九.直线与圆锥曲线的综合(共2小题)
10.(2022 浙江)如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=﹣x+3于C,D两点.
(Ⅰ)求点P到椭圆上点的距离的最大值;
(Ⅱ)求|CD|的最小值.
11.(2021 浙江)如图,已知F是抛物线y2=2px(p>0)的焦点,M是抛物线的准线与x轴的交点,且|MF|=2.
(Ⅰ)求抛物线的方程:
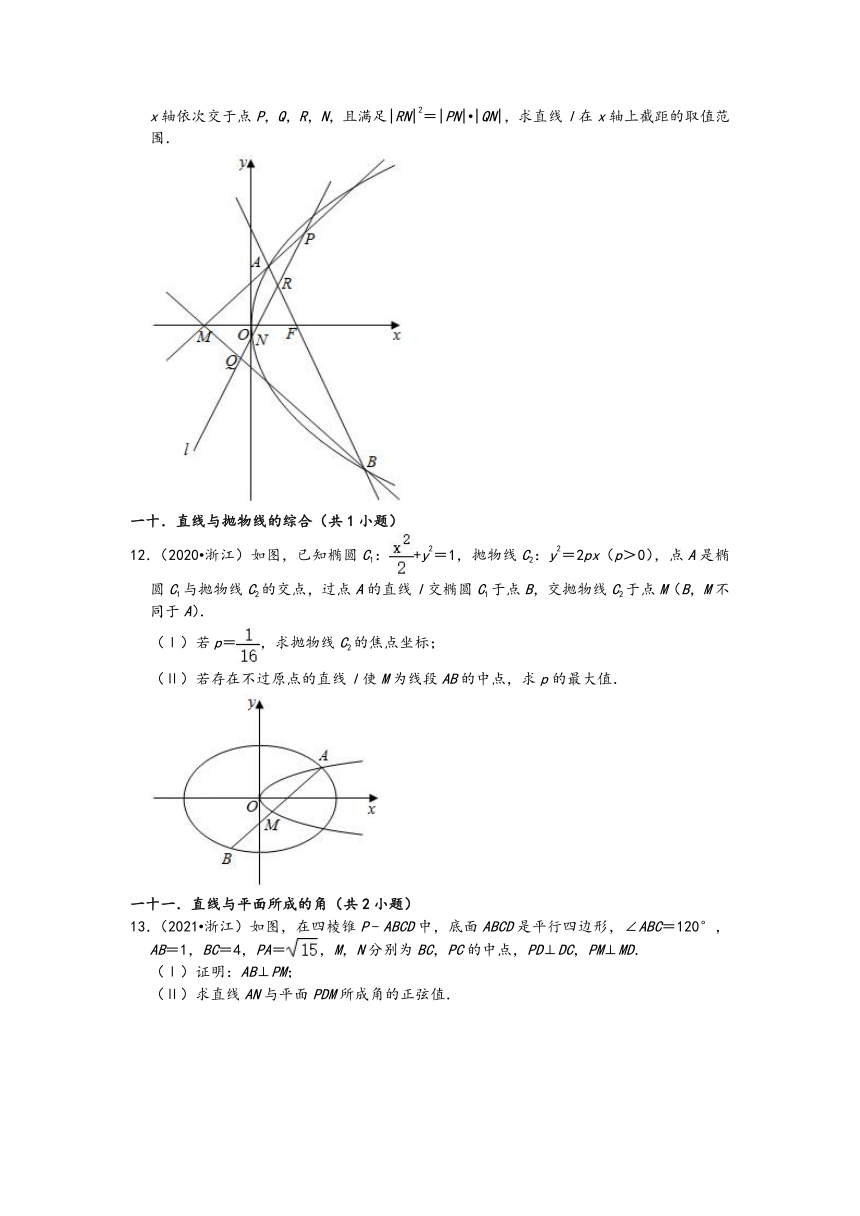
(Ⅱ)设过点F的直线交抛物线于A,B两点,若斜率为2的直线l与直线MA,MB,AB,x轴依次交于点P,Q,R,N,且满足|RN|2=|PN| |QN|,求直线l在x轴上截距的取值范围.
一十.直线与抛物线的综合(共1小题)
12.(2020 浙江)如图,已知椭圆C1:+y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于点M(B,M不同于A).
(Ⅰ)若p=,求抛物线C2的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
一十一.直线与平面所成的角(共2小题)
13.(2021 浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(Ⅰ)证明:AB⊥PM;
(Ⅱ)求直线AN与平面PDM所成角的正弦值.
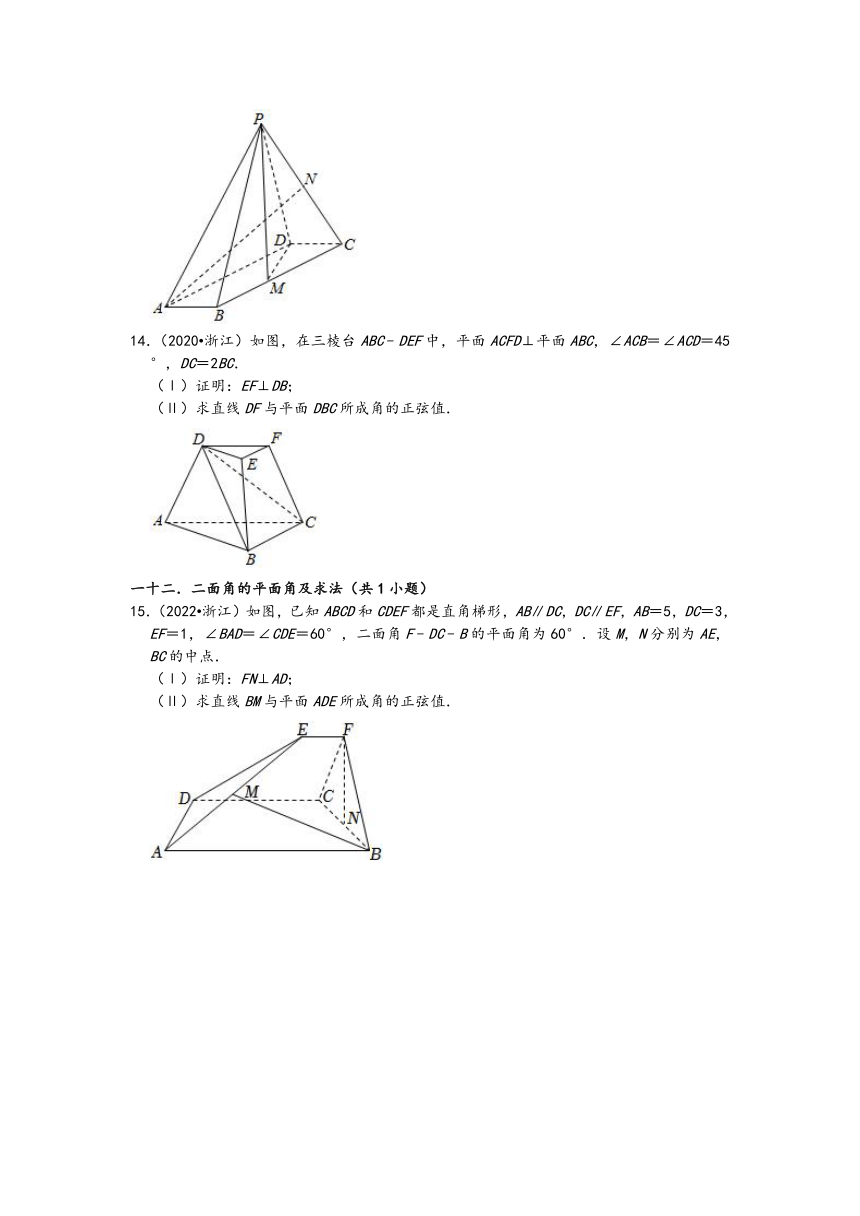
14.(2020 浙江)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
一十二.二面角的平面角及求法(共1小题)
15.(2022 浙江)如图,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F﹣DC﹣B的平面角为60°.设M,N分别为AE,BC的中点.
(Ⅰ)证明:FN⊥AD;
(Ⅱ)求直线BM与平面ADE所成角的正弦值.
参考答案与试题解析
一.利用导数研究函数的单调性(共2小题)
1.(2022 浙江)设函数f(x)=+lnx(x>0).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)已知a,b∈R,曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:
(ⅰ)若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)若0<a<e,x1<x2<x3,则+<+<﹣.
(注:e=2.71828…是自然对数的底数)
【解析】解:(Ⅰ)∵函数f(x)=+lnx(x>0),
∴+=,(x>0),
由>0,得x>,∴f(x)在(,+∞)上单调递增;
由<0,得0<x<,∴f(x)在(0,)上单调递减.
(Ⅱ)(i)证明:设经过点(a,b)的直线与函数f(x)的图象相切时切点坐标为(),
则切线方程为l:﹣lnx0=f′(x0)(x﹣x0),
∵,∴切线l的方程为(﹣)x﹣y+,
∴(﹣)a﹣b++lnx0﹣1=0,
令g(x)=(﹣)﹣a+b++lnx﹣1,(x>0),
∵曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b),
∴函数g(x)有三个不同的零点,
∵=,
∵a>e,∴x<e,或x>a时,g′(x)>0,g(x)单调递增,
e<x<a时,g′(x)<0,g(x)单调递减,从而g(x)极大值=g(e)>0,g(x)极小值=g(a)<0,
∴,且②,
由②得b﹣f(a)=b﹣,由①有b<,
∵b﹣f(a)=b﹣,∴要证明b﹣f(a)<,
只需证明,即lna+,
令h(a)=lna+,则=>0,∴h(a)单调递增,
∴h(a)>h(e)=,∴b﹣f(a)<(),
综上,若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)证明:由(i)知g(x)=(﹣+)a﹣b++lnx﹣1(x>0)有三个不同的零点,
设=t,则g(x)化为h(t)=(﹣)a﹣b+et﹣lnt﹣1,
h(t)在三个不同的零点t1,t2,t3,且t1>t2>t3,
∵h(t1)=h(t3),∴e(t1﹣t3)﹣ln+,
∴,
解得 ,③
要证明结论,只需证明[][t1+t3﹣()]≤0,
即,
把③式代入得只需证明(e+a﹣) (t1+t3)+()()≤0,
即﹣()≤0,
令=s,由题意得s>,
当s>时,=2 ,(n=),
∴只需证明,
∵lnn>,
∴
>[2n﹣(1﹣)]
=>>0,
∴+<+<﹣.
2.(2021 浙江)设a,b为实数,且a>1,函数f(x)=ax﹣bx+e2(x∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围;
(Ⅲ)当a=e时,证明:对任意b>e4,函数f(x)有两个不同的零点x1,x2,满足x2>x1+.
(注:e=2.71828 是自然对数的底数)
【解析】解:(Ⅰ)f′(x)=axlna﹣b,
①当b≤0时,由于a>1,则axlna>0,故f′(x)>0,此时f(x)在R上单调递增;
②当b>0时,令f′(x)>0,解得,令f′(x)<0,解得,
∴此时f(x)在单调递减,在单调递增;
综上,当b≤0时,f(x)的单调递增区间为(﹣∞,+∞);当b>0时,f(x)的单调递减区间为,单调递增区间为;
(Ⅱ)注意到x→﹣∞时,f(x)→+∞,当x→+∞时,f(x)→+∞,
由(Ⅰ)知,要使函数f(x)有两个不同的零点,只需即可,
∴对任意b>2e2均成立,
令,则at﹣bt+e2<0,即etlna﹣bt+e2<0,即,即,
∴对任意b>2e2均成立,
记,则,
令g′(b)=0,得b=lna,
①当lna>2e2,即时,易知g(b)在(2e2,lna)单调递增,在(lna,+∞)单调递减,
此时g(b)≤g(lna)=lna﹣lna ln1+e2lna=lna (e2+1)>0,不合题意;
②当lna≤2e2,即时,易知g(b)在(2e2,+∞)单调递减,
此时=2e2﹣2e2[ln(2e2)﹣ln(lna)]+e2lna,
故只需2﹣2[ln2+2﹣ln(lna)]+lna≤0,即lna+2ln(lna)≤2+2ln2,则lna≤2,即a≤e2;
综上,实数a的取值范围为(1,e2];
(Ⅲ)证明:当a=e时,f(x)=ex﹣bx+e2,f′(x)=ex﹣b,令f′(x)=0,解得x=lnb>4,
易知+e2=e2﹣3b<e2﹣3e4=e2(1﹣3e2)<0,
∴f(x)有两个零点,不妨设为x1,x2,且x1<lnb<x2,
由,可得,
∴要证,只需证,只需证,
而,则,
∴要证,只需证,只需证x2>ln(blnb),
而f(ln(blnb))=eln(blnb)﹣bln(blnb)+e2=blnb﹣bln(blnb)+e2<blnb﹣bln(4b)+e2=,
∴x2>ln(blnb),即得证.
二.利用导数研究函数的最值(共1小题)
3.(2020 浙江)已知1<a≤2,函数f(x)=ex﹣x﹣a,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数y=f(x)在(0,+∞)上有唯一零点;
(Ⅱ)记x0为函数y=f(x)在(0,+∞)上的零点,证明:
(ⅰ)≤x0≤;
(ⅱ)x0f(e)≥(e﹣1)(a﹣1)a.
【解析】证明:(Ⅰ)∵f(x)=ex﹣x﹣a=0(x>0),∴f′(x)=ex﹣1>0恒成立,
∴f(x)在(0,+∞)上单调递增,
∵1<a≤2,∴f(2)=e2﹣2﹣a≥e2﹣4>0,又f(0)=1﹣a<0,
∴函数y=f(x)在 (0,+∞)上有唯一零点.
(Ⅱ)(i)f(x0)=0,∴﹣x0﹣a=0,
∴,∴,
令g(x)=ex﹣x﹣1﹣x2(0<x<2),h(x)=ex﹣x﹣1﹣,(0<x<2),
一方面,h′(x)=ex﹣1﹣x=h1(x),,
∴h′(x)>h′(0)=0,∴h(x)在(0,2)单调递增,
∴h(x)>h(0)=0,
∴ex﹣x﹣1﹣>0,2(ex﹣x﹣1)>x2,
另一方面,1<a≤2,∴0<a﹣1≤1,
∴当x0≥1时,成立,
∴只需证明当0<x<1时,g(x)=ex﹣x﹣1﹣x2≤0,
∵g′(x)=ex﹣1﹣2x=g1(x),g1'(x)=ex﹣2=0,∴x=ln2,
当x∈(0,ln2)时,g1'(x)<0,当x∈(ln2,1)时,g1'(x)>0,
∴g′(x)<max{g′(0),g′(1)},g′(0)=0,g′(1)=e﹣3<0,
∴g′(x)<0,∴g(x)在(0,1)单调递减,
∴g(x)<g(0)=0,∴ex﹣x﹣1<x2,
综上,,
∴≤x0≤.
(ii)要证明x0f(e)≥(e﹣1)(a﹣1)a,只需证x0f(x0+a)≥(e﹣1)(a﹣1)a,
由(i)得只需证﹣≥(e﹣1)a,
∵ex≥1+x+,∴只需证1+()2﹣a≥(e﹣1)a,
只需证﹣2(e﹣2)a≥0,即证﹣≥2(e﹣2),
∵=+∈[2,+∞),
∴≥=,
∴x0f(e)≥(e﹣1)(a﹣1)a.
三.数列的求和(共1小题)
4.(2020 浙江)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1﹣an,cn+1=cn(n∈N*).
(Ⅰ)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(Ⅱ)若{bn}为等差数列,公差d>0,证明:c1+c2+c3+…+cn<1+,n∈N*.
【解析】(Ⅰ)解:由题意,b2=q,b3=q2,
∵b1+b2=6b3,∴1+q=6q2,
整理,得6q2﹣q﹣1=0,
解得q=﹣(舍去),或q=,
∴cn+1= cn= cn= cn= cn=4 cn,
∴数列{cn}是以1为首项,4为公比的等比数列,
∴cn=1 4n﹣1=4n﹣1,n∈N*.
∴an+1﹣an=cn=4n﹣1,
则a1=1,
a2﹣a1=1,
a3﹣a2=41,
…
an﹣an﹣1=4n﹣2,
各项相加,可得
an=1+1+41+42+…+4n﹣2=+1=.
(Ⅱ)证明:依题意,由cn+1= cn(n∈N*),可得
bn+2 cn+1=bn cn,
两边同时乘以bn+1,可得
bn+1bn+2cn+1=bnbn+1cn,
∵b1b2c1=b2=1+d,
∴数列{bnbn+1cn}是一个常数列,且此常数为1+d,
bnbn+1cn=1+d,
∴cn== =(1+) =(1+)(﹣),
又∵b1=1,d>0,
∴bn>0,
∴c1+c2+…+cn
=(1+)(﹣)+(1+)(﹣)+…+(1+)(﹣)
=(1+)(﹣+﹣+…+﹣)
=(1+)(﹣)
=(1+)(1﹣)
<1+,
∴c1+c2+…+cn<1+,故得证.
四.数列递推式(共1小题)
5.(2021 浙江)已知数列{an}的前n项和为Sn,a1=﹣,且4Sn+1=3Sn﹣9(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足3bn+(n﹣4)an=0(n∈N*),记{bn}的前n项和为Tn,若Tn≤λbn对任意n∈N*恒成立,
求实数λ的取值范围.
【解析】解:(Ⅰ)由4Sn+1=3Sn﹣9 可得4Sn=3Sn﹣1﹣9(n≥2),
两式作差,可得:4an+1=3an,
∴,
很明显,,
所以数列{an} 是以 为首项,为公比的等比数列,
其通项公式为:(n≥1,n∈N*).
(Ⅱ)由3bn+(n﹣4)an=0,得,
,
,
两式作差可得:
=
=,
则.
据此可得 恒成立,即λ(n﹣4)+3n≥0 恒成立.
n=4时不等式成立;
n<4时,,由于n=1时,故λ≤1;
n>4时,,而,故:λ≥﹣3;
综上可得,{λ|﹣3≤λ≤1}.
五.等差数列与等比数列的综合(共1小题)
6.(2022 浙江)已知等差数列{an}的首项a1=﹣1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(Ⅰ)若S4﹣2a2a3+6=0,求Sn;
(Ⅱ)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
【解析】解:(Ⅰ)因为等差数列{an}的首项a1=﹣1,公差d>1,
因为S4﹣2a2a3+6=0,可得﹣2a2a3+6=0,即2(a1+a4)﹣2a2a3+6=0,
a1+a1+3d﹣(a1+d)(a1+2d)+3=0,即﹣1﹣1+3d﹣(﹣1+d)(﹣1+2d)+3=0,
整理可得:d2=3d,解得d=3,
所以Sn=na1+d=﹣n+=,
即Sn=;
(Ⅱ)因为对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,
则(a1+nd+4cn)2=[a1+(n﹣1)d+cn][(a1+(n+1)d+15cn],a1=﹣1,
整理可得:cn2+[(14﹣8n)d+8]cn+d2=0,则Δ=[(14﹣8n)d+8]2﹣4d2≥0,
即(7﹣4n)d+4≥d或(7﹣4n)d+4≤﹣d,
整理可得(3﹣2n)d≥﹣2或(2﹣n)d≤﹣1,
当n=1时,可得d≥﹣2或d≤﹣1,而d>1,
所以d≤﹣1(舍),
所以d的范围为(1,+∞);
n=2时,d≤2或 ,而d>1,
所以此时d∈(1,2],
当n为大于2的任何整数,d≤或d≥,而d>1,
所以d≤(舍),d>1恒成立;
综上所述,n=2时,d∈(1,2];
n为不等于2的正整数时,d的取值范围为(1,+∞),都存在cn,使an+cn,an+1+4cn,an+2+15cn成等比数列.
六.三角函数中的恒等变换应用(共1小题)
7.(2021 浙江)设函数f(x)=sinx+cosx(x∈R).
(Ⅰ)求函数y=[f(x+)]2的最小正周期;
(Ⅱ)求函数y=f(x)f(x﹣)在[0,]上的最大值.
【解析】解:函数f(x)=sinx+cosx=,
(Ⅰ)函数y=[f(x+)]2=[2=2cos2(x+)
=1+cos[2(x+)]=1+cos(2x+)=1﹣sin2x,
则最小正周期为T=;
(Ⅱ)函数y=f(x)f(x﹣)=
=sinx+cosx)sinx=
==sin(2x﹣)+,
因为x,所以2x﹣,
所以当2x﹣,即x=时,ymax=1+.
七.正弦定理(共1小题)
8.(2020 浙江)在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知2bsinA﹣a=0.
(Ⅰ)求角B的大小;
(Ⅱ)求cosA+cosB+cosC的取值范围.
【解析】解:(Ⅰ)∵2bsinA=a,
∴2sinBsinA=sinA,
∵sinA≠0,
∴sinB=,
∵△ABC为锐角三角形,
∴B=,
(Ⅱ)∵△ABC为锐角三角形,B=,
∴C=﹣A,
∴cosA+cosB+cosC=cosA+cos(﹣A)+cos=cosA﹣cosA+sinA+=cosA+sinA+=sin(A+)+,
△ABC为锐角三角形,0<A<,0<C<,
解得<A<,
∴<A+<,
∴<sin(A+)≤1,
∴+<sin(A+)+≤,
∴cosA+cosB+cosC的取值范围为(,].
八.三角形中的几何计算(共1小题)
9.(2022 浙江)在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
【解析】解:(Ⅰ)因为cosC=>0,所以C∈(0,),且sinC==,
由正弦定理可得:=,
即有sinA==sinC=×=;
(Ⅱ)因为4a=c a=c<c,
所以A<C,故A∈(0,),
又因为sinA=,所以cosA=,
所以sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC=;
由正弦定理可得:===5,
所以a=5sinA=5,
所以S△ABC=absinC=×5×11×=22.
九.直线与圆锥曲线的综合(共2小题)
10.(2022 浙江)如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=﹣x+3于C,D两点.
(Ⅰ)求点P到椭圆上点的距离的最大值;
(Ⅱ)求|CD|的最小值.
【解析】解:(Ⅰ)设椭圆上任意一点M(x,y),则|PM|2=x2+(y﹣1)2=12﹣12y2+y2﹣2y+1=﹣11y2﹣2y+13,y∈[﹣1,1],
而函数z=﹣11y2﹣2y+13的对称轴为,则其最大值为,
∴,即点P到椭圆上点的距离的最大值为;
(Ⅱ)设直线AB:,
联立直线AB与椭圆方程有,消去y并整理可得,(12k2+1)x2+12kx﹣9=0,
由韦达定理可得,,
∴=,
设C(x3,y3),D(x4,y4),直线AP:,直线BP:,
联立以及,
可得,
∴由弦长公式可得====,当且仅当时等号成立,
∴|CD|的最小值为.
11.(2021 浙江)如图,已知F是抛物线y2=2px(p>0)的焦点,M是抛物线的准线与x轴的交点,且|MF|=2.
(Ⅰ)求抛物线的方程:
(Ⅱ)设过点F的直线交抛物线于A,B两点,若斜率为2的直线l与直线MA,MB,AB,x轴依次交于点P,Q,R,N,且满足|RN|2=|PN| |QN|,求直线l在x轴上截距的取值范围.
【解析】解:(Ⅰ)依题意,p=2,故抛物线的方程为y2=4x;
(Ⅱ)由题意得,直线AB的斜率存在且不为零,设直线AB:y=k(x﹣1),
将直线AB方程代入抛物线方程可得,k2x2﹣(2k2+4)x+k2=0,
则由韦达定理有,,则yAyB=﹣4,
设直线AM:y=k1(x+1),其中,设直线BM:y=k2(x+1),其中,
则===,
,
设直线l:y=2(x﹣t),
联立,可得,则,
联立,可得,则,
同理可得,,
又|RN|2=|PN| |QN|,
∴,即,
∴=(t≠1),
∴4(t2+2t+1)≥3(t2﹣2t+1),即t2+14t+1≥0,解得或(t≠1);
当直线AB的斜率不存在时,则直线AB:x=1,A(1,2),B(1,﹣2),M(﹣1,0),
∴直线MA的方程为y=x+1,直线MB的方程为y=﹣x﹣1,
设直线l:y=2(x﹣t),则P(1+2t,2+2t),,R(1,2﹣2t),N(t,0),
又|RN|2=|PN| |QN|,故,
解得t满足.
∴直线l在x轴上截距的取值范围为.
一十.直线与抛物线的综合(共1小题)
12.(2020 浙江)如图,已知椭圆C1:+y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于点M(B,M不同于A).
(Ⅰ)若p=,求抛物线C2的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
【解析】解:(Ⅰ)p=,则=,则抛物线C2的焦点坐标(,0),
(Ⅱ)直线l与x轴垂直时,此时点M与点A或点B重合,不满足题意,
设直线l的方程为y=kx+t,A(x1,y1),B(x2,y2),M(x0,y0),
由,消y可得(2k2+1)x2+4ktx+2t2﹣2=0,
∴Δ=16k2t2﹣4(2k2+1)(2t2﹣2)>0,即t2<1+2k2,
∴x1+x2=﹣,∴x0=(x1+x2)=﹣,
∴y0=kx0+t=,∴M(﹣,),
∵点M在抛物线C2上,∴y2=2px,
∴p===,
联立,解得x1=,y1=,
代入椭圆方程可得+=1,解得t2=
∴p2==
=≤=,
∴p≤,当且仅当1=2k2,即k2=,t2=时等号成立,
故p的最大值为.
一十一.直线与平面所成的角(共2小题)
13.(2021 浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(Ⅰ)证明:AB⊥PM;
(Ⅱ)求直线AN与平面PDM所成角的正弦值.
【解析】(Ⅰ)证明:在平行四边形ABCD中,由已知可得,CD=AB=1,
CM=BC=2,∠DCM=60°,
∴由余弦定理可得,DM2=CD2+CM2﹣2CD×CM×cos60°
=,
则CD2+DM2=1+3=4=CM2,即CD⊥DM,
又PD⊥DC,PD∩DM=D,∴CD⊥平面PDM,
而PM 平面PDM,∴CD⊥PM,
∵CD∥AB,∴AB⊥PM;
(Ⅱ)解:由(Ⅰ)知,CD⊥平面PDM,
又CD 平面ABCD,∴平面ABCD⊥平面PDM,
且平面ABCD∩平面PDM=DM,
∵PM⊥MD,且PM 平面PDM,∴PM⊥平面ABCD,
连接AM,则PM⊥MA,
在△ABM中,AB=1,BM=2,∠ABM=120°,
可得,
又PA=,在Rt△PMA中,求得PM=,
取AD中点E,连接ME,则ME∥CD,可得ME、MD、MP两两互相垂直,
以M为坐标原点,分别以MD、ME、MP为x、y、z轴建立空间直角坐标系,
则A(,2,0),P(0,0,),C(),
又N为PC的中点,∴N(),,
平面PDM的一个法向量为,
设直线AN与平面PDM所成角为θ,
则sinθ=|cos<>|==.
故直线AN与平面PDM所成角的正弦值为.
14.(2020 浙江)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
【解析】解:(Ⅰ)证明:作DH⊥AC,且交AC于点H,
∵面ADFC⊥面ABC,DH 面ADFC,∴DH⊥BC,
∴在Rt△DHC中,CH=CD cos45°=CD,
∵DC=2BC,∴CH=CD= 2BC= BC,
∴=,即△BHC是直角三角形,且∠HBC=90°,
∴HB⊥BC,∴BC⊥面DHB,∵BD 面DHB,∴BC⊥BD,
∵在三棱台DEF﹣ABC中,EF∥BC,∴EF⊥DB.
(Ⅱ)设BC=1,则BH=1,HC=,
在Rt△DHC中,DH=,DC=2,
在Rt△DHB中,DB===,
作HG⊥BD于G,∵BC⊥HG,∴HG⊥面BCD,∵GC 面BCD,
∴HG⊥GC,∴△HGC是直角三角形,且∠HGC=90°,
设DF与面DBC所成角为θ,则θ即为CH与面DBC的夹角,
且sinθ=sin∠HCG==,
∵在Rt△DHB中,DH HB=BD HG,
∴HG===,
∴sinθ===.
一十二.二面角的平面角及求法(共1小题)
15.(2022 浙江)如图,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F﹣DC﹣B的平面角为60°.设M,N分别为AE,BC的中点.
(Ⅰ)证明:FN⊥AD;
(Ⅱ)求直线BM与平面ADE所成角的正弦值.
【解析】证明:(I)由于CD⊥CB,CD⊥CF,
平面ABCD∩平面CDEF=CD,CF 平面CDEF,CB 平面ABCD,
所以∠FCB为二面角F﹣DC﹣B的平面角,
则∠FCB=60°,CD⊥平面CBF,则CD⊥FN.
又,
则△BCF是等边三角形,则CB⊥FN,
因为DC⊥FC,DC⊥BC,FC∩BC=C,FC 平面FCB,BC 平面FCB,
所以DC⊥平面FCB,因为FN 平面FCB,所以DC⊥FN,
又因为DC∩CB=C,DC 平面ABCD,CB 平面ABCD,
所以FN⊥平面ABCD,因为AD 平面ABCD,故FN⊥AD;
解:(Ⅱ)由于FN⊥平面ABCD,如图建系:
于是,则,
,
设平面ADE的法向量=(x,y,z),
则,∴,令x=,则y=﹣1,z=,
∴平面ADE的法向量,
设BM与平面ADE所成角为θ,
则.
一.利用导数研究函数的单调性(共2小题)
1.(2022 浙江)设函数f(x)=+lnx(x>0).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)已知a,b∈R,曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:
(ⅰ)若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)若0<a<e,x1<x2<x3,则+<+<﹣.
(注:e=2.71828…是自然对数的底数)
2.(2021 浙江)设a,b为实数,且a>1,函数f(x)=ax﹣bx+e2(x∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围;
(Ⅲ)当a=e时,证明:对任意b>e4,函数f(x)有两个不同的零点x1,x2,满足x2>x1+.
(注:e=2.71828 是自然对数的底数)
二.利用导数研究函数的最值(共1小题)
3.(2020 浙江)已知1<a≤2,函数f(x)=ex﹣x﹣a,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数y=f(x)在(0,+∞)上有唯一零点;
(Ⅱ)记x0为函数y=f(x)在(0,+∞)上的零点,证明:
(ⅰ)≤x0≤;
(ⅱ)x0f(e)≥(e﹣1)(a﹣1)a.
三.数列的求和(共1小题)
4.(2020 浙江)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1﹣an,cn+1=cn(n∈N*).
(Ⅰ)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(Ⅱ)若{bn}为等差数列,公差d>0,证明:c1+c2+c3+…+cn<1+,n∈N*.
四.数列递推式(共1小题)
5.(2021 浙江)已知数列{an}的前n项和为Sn,a1=﹣,且4Sn+1=3Sn﹣9(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足3bn+(n﹣4)an=0(n∈N*),记{bn}的前n项和为Tn,若Tn≤λbn对任意n∈N*恒成立,
求实数λ的取值范围.
五.等差数列与等比数列的综合(共1小题)
6.(2022 浙江)已知等差数列{an}的首项a1=﹣1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(Ⅰ)若S4﹣2a2a3+6=0,求Sn;
(Ⅱ)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
六.三角函数中的恒等变换应用(共1小题)
7.(2021 浙江)设函数f(x)=sinx+cosx(x∈R).
(Ⅰ)求函数y=[f(x+)]2的最小正周期;
(Ⅱ)求函数y=f(x)f(x﹣)在[0,]上的最大值.
七.正弦定理(共1小题)
8.(2020 浙江)在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知2bsinA﹣a=0.
(Ⅰ)求角B的大小;
(Ⅱ)求cosA+cosB+cosC的取值范围.
八.三角形中的几何计算(共1小题)
9.(2022 浙江)在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
九.直线与圆锥曲线的综合(共2小题)
10.(2022 浙江)如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=﹣x+3于C,D两点.
(Ⅰ)求点P到椭圆上点的距离的最大值;
(Ⅱ)求|CD|的最小值.
11.(2021 浙江)如图,已知F是抛物线y2=2px(p>0)的焦点,M是抛物线的准线与x轴的交点,且|MF|=2.
(Ⅰ)求抛物线的方程:
(Ⅱ)设过点F的直线交抛物线于A,B两点,若斜率为2的直线l与直线MA,MB,AB,x轴依次交于点P,Q,R,N,且满足|RN|2=|PN| |QN|,求直线l在x轴上截距的取值范围.
一十.直线与抛物线的综合(共1小题)
12.(2020 浙江)如图,已知椭圆C1:+y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于点M(B,M不同于A).
(Ⅰ)若p=,求抛物线C2的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
一十一.直线与平面所成的角(共2小题)
13.(2021 浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(Ⅰ)证明:AB⊥PM;
(Ⅱ)求直线AN与平面PDM所成角的正弦值.
14.(2020 浙江)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
一十二.二面角的平面角及求法(共1小题)
15.(2022 浙江)如图,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F﹣DC﹣B的平面角为60°.设M,N分别为AE,BC的中点.
(Ⅰ)证明:FN⊥AD;
(Ⅱ)求直线BM与平面ADE所成角的正弦值.
参考答案与试题解析
一.利用导数研究函数的单调性(共2小题)
1.(2022 浙江)设函数f(x)=+lnx(x>0).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)已知a,b∈R,曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b).证明:
(ⅰ)若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)若0<a<e,x1<x2<x3,则+<+<﹣.
(注:e=2.71828…是自然对数的底数)
【解析】解:(Ⅰ)∵函数f(x)=+lnx(x>0),
∴+=,(x>0),
由>0,得x>,∴f(x)在(,+∞)上单调递增;
由<0,得0<x<,∴f(x)在(0,)上单调递减.
(Ⅱ)(i)证明:设经过点(a,b)的直线与函数f(x)的图象相切时切点坐标为(),
则切线方程为l:﹣lnx0=f′(x0)(x﹣x0),
∵,∴切线l的方程为(﹣)x﹣y+,
∴(﹣)a﹣b++lnx0﹣1=0,
令g(x)=(﹣)﹣a+b++lnx﹣1,(x>0),
∵曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b),
∴函数g(x)有三个不同的零点,
∵=,
∵a>e,∴x<e,或x>a时,g′(x)>0,g(x)单调递增,
e<x<a时,g′(x)<0,g(x)单调递减,从而g(x)极大值=g(e)>0,g(x)极小值=g(a)<0,
∴,且②,
由②得b﹣f(a)=b﹣,由①有b<,
∵b﹣f(a)=b﹣,∴要证明b﹣f(a)<,
只需证明,即lna+,
令h(a)=lna+,则=>0,∴h(a)单调递增,
∴h(a)>h(e)=,∴b﹣f(a)<(),
综上,若a>e,则0<b﹣f(a)<(﹣1);
(ⅱ)证明:由(i)知g(x)=(﹣+)a﹣b++lnx﹣1(x>0)有三个不同的零点,
设=t,则g(x)化为h(t)=(﹣)a﹣b+et﹣lnt﹣1,
h(t)在三个不同的零点t1,t2,t3,且t1>t2>t3,
∵h(t1)=h(t3),∴e(t1﹣t3)﹣ln+,
∴,
解得 ,③
要证明结论,只需证明[][t1+t3﹣()]≤0,
即,
把③式代入得只需证明(e+a﹣) (t1+t3)+()()≤0,
即﹣()≤0,
令=s,由题意得s>,
当s>时,=2 ,(n=),
∴只需证明,
∵lnn>,
∴
>[2n﹣(1﹣)]
=>>0,
∴+<+<﹣.
2.(2021 浙江)设a,b为实数,且a>1,函数f(x)=ax﹣bx+e2(x∈R).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意b>2e2,函数f(x)有两个不同的零点,求a的取值范围;
(Ⅲ)当a=e时,证明:对任意b>e4,函数f(x)有两个不同的零点x1,x2,满足x2>x1+.
(注:e=2.71828 是自然对数的底数)
【解析】解:(Ⅰ)f′(x)=axlna﹣b,
①当b≤0时,由于a>1,则axlna>0,故f′(x)>0,此时f(x)在R上单调递增;
②当b>0时,令f′(x)>0,解得,令f′(x)<0,解得,
∴此时f(x)在单调递减,在单调递增;
综上,当b≤0时,f(x)的单调递增区间为(﹣∞,+∞);当b>0时,f(x)的单调递减区间为,单调递增区间为;
(Ⅱ)注意到x→﹣∞时,f(x)→+∞,当x→+∞时,f(x)→+∞,
由(Ⅰ)知,要使函数f(x)有两个不同的零点,只需即可,
∴对任意b>2e2均成立,
令,则at﹣bt+e2<0,即etlna﹣bt+e2<0,即,即,
∴对任意b>2e2均成立,
记,则,
令g′(b)=0,得b=lna,
①当lna>2e2,即时,易知g(b)在(2e2,lna)单调递增,在(lna,+∞)单调递减,
此时g(b)≤g(lna)=lna﹣lna ln1+e2lna=lna (e2+1)>0,不合题意;
②当lna≤2e2,即时,易知g(b)在(2e2,+∞)单调递减,
此时=2e2﹣2e2[ln(2e2)﹣ln(lna)]+e2lna,
故只需2﹣2[ln2+2﹣ln(lna)]+lna≤0,即lna+2ln(lna)≤2+2ln2,则lna≤2,即a≤e2;
综上,实数a的取值范围为(1,e2];
(Ⅲ)证明:当a=e时,f(x)=ex﹣bx+e2,f′(x)=ex﹣b,令f′(x)=0,解得x=lnb>4,
易知+e2=e2﹣3b<e2﹣3e4=e2(1﹣3e2)<0,
∴f(x)有两个零点,不妨设为x1,x2,且x1<lnb<x2,
由,可得,
∴要证,只需证,只需证,
而,则,
∴要证,只需证,只需证x2>ln(blnb),
而f(ln(blnb))=eln(blnb)﹣bln(blnb)+e2=blnb﹣bln(blnb)+e2<blnb﹣bln(4b)+e2=,
∴x2>ln(blnb),即得证.
二.利用导数研究函数的最值(共1小题)
3.(2020 浙江)已知1<a≤2,函数f(x)=ex﹣x﹣a,其中e=2.71828…为自然对数的底数.
(Ⅰ)证明:函数y=f(x)在(0,+∞)上有唯一零点;
(Ⅱ)记x0为函数y=f(x)在(0,+∞)上的零点,证明:
(ⅰ)≤x0≤;
(ⅱ)x0f(e)≥(e﹣1)(a﹣1)a.
【解析】证明:(Ⅰ)∵f(x)=ex﹣x﹣a=0(x>0),∴f′(x)=ex﹣1>0恒成立,
∴f(x)在(0,+∞)上单调递增,
∵1<a≤2,∴f(2)=e2﹣2﹣a≥e2﹣4>0,又f(0)=1﹣a<0,
∴函数y=f(x)在 (0,+∞)上有唯一零点.
(Ⅱ)(i)f(x0)=0,∴﹣x0﹣a=0,
∴,∴,
令g(x)=ex﹣x﹣1﹣x2(0<x<2),h(x)=ex﹣x﹣1﹣,(0<x<2),
一方面,h′(x)=ex﹣1﹣x=h1(x),,
∴h′(x)>h′(0)=0,∴h(x)在(0,2)单调递增,
∴h(x)>h(0)=0,
∴ex﹣x﹣1﹣>0,2(ex﹣x﹣1)>x2,
另一方面,1<a≤2,∴0<a﹣1≤1,
∴当x0≥1时,成立,
∴只需证明当0<x<1时,g(x)=ex﹣x﹣1﹣x2≤0,
∵g′(x)=ex﹣1﹣2x=g1(x),g1'(x)=ex﹣2=0,∴x=ln2,
当x∈(0,ln2)时,g1'(x)<0,当x∈(ln2,1)时,g1'(x)>0,
∴g′(x)<max{g′(0),g′(1)},g′(0)=0,g′(1)=e﹣3<0,
∴g′(x)<0,∴g(x)在(0,1)单调递减,
∴g(x)<g(0)=0,∴ex﹣x﹣1<x2,
综上,,
∴≤x0≤.
(ii)要证明x0f(e)≥(e﹣1)(a﹣1)a,只需证x0f(x0+a)≥(e﹣1)(a﹣1)a,
由(i)得只需证﹣≥(e﹣1)a,
∵ex≥1+x+,∴只需证1+()2﹣a≥(e﹣1)a,
只需证﹣2(e﹣2)a≥0,即证﹣≥2(e﹣2),
∵=+∈[2,+∞),
∴≥=,
∴x0f(e)≥(e﹣1)(a﹣1)a.
三.数列的求和(共1小题)
4.(2020 浙江)已知数列{an},{bn},{cn}满足a1=b1=c1=1,cn=an+1﹣an,cn+1=cn(n∈N*).
(Ⅰ)若{bn}为等比数列,公比q>0,且b1+b2=6b3,求q的值及数列{an}的通项公式;
(Ⅱ)若{bn}为等差数列,公差d>0,证明:c1+c2+c3+…+cn<1+,n∈N*.
【解析】(Ⅰ)解:由题意,b2=q,b3=q2,
∵b1+b2=6b3,∴1+q=6q2,
整理,得6q2﹣q﹣1=0,
解得q=﹣(舍去),或q=,
∴cn+1= cn= cn= cn= cn=4 cn,
∴数列{cn}是以1为首项,4为公比的等比数列,
∴cn=1 4n﹣1=4n﹣1,n∈N*.
∴an+1﹣an=cn=4n﹣1,
则a1=1,
a2﹣a1=1,
a3﹣a2=41,
…
an﹣an﹣1=4n﹣2,
各项相加,可得
an=1+1+41+42+…+4n﹣2=+1=.
(Ⅱ)证明:依题意,由cn+1= cn(n∈N*),可得
bn+2 cn+1=bn cn,
两边同时乘以bn+1,可得
bn+1bn+2cn+1=bnbn+1cn,
∵b1b2c1=b2=1+d,
∴数列{bnbn+1cn}是一个常数列,且此常数为1+d,
bnbn+1cn=1+d,
∴cn== =(1+) =(1+)(﹣),
又∵b1=1,d>0,
∴bn>0,
∴c1+c2+…+cn
=(1+)(﹣)+(1+)(﹣)+…+(1+)(﹣)
=(1+)(﹣+﹣+…+﹣)
=(1+)(﹣)
=(1+)(1﹣)
<1+,
∴c1+c2+…+cn<1+,故得证.
四.数列递推式(共1小题)
5.(2021 浙江)已知数列{an}的前n项和为Sn,a1=﹣,且4Sn+1=3Sn﹣9(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{bn}满足3bn+(n﹣4)an=0(n∈N*),记{bn}的前n项和为Tn,若Tn≤λbn对任意n∈N*恒成立,
求实数λ的取值范围.
【解析】解:(Ⅰ)由4Sn+1=3Sn﹣9 可得4Sn=3Sn﹣1﹣9(n≥2),
两式作差,可得:4an+1=3an,
∴,
很明显,,
所以数列{an} 是以 为首项,为公比的等比数列,
其通项公式为:(n≥1,n∈N*).
(Ⅱ)由3bn+(n﹣4)an=0,得,
,
,
两式作差可得:
=
=,
则.
据此可得 恒成立,即λ(n﹣4)+3n≥0 恒成立.
n=4时不等式成立;
n<4时,,由于n=1时,故λ≤1;
n>4时,,而,故:λ≥﹣3;
综上可得,{λ|﹣3≤λ≤1}.
五.等差数列与等比数列的综合(共1小题)
6.(2022 浙江)已知等差数列{an}的首项a1=﹣1,公差d>1.记{an}的前n项和为Sn(n∈N*).
(Ⅰ)若S4﹣2a2a3+6=0,求Sn;
(Ⅱ)若对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,求d的取值范围.
【解析】解:(Ⅰ)因为等差数列{an}的首项a1=﹣1,公差d>1,
因为S4﹣2a2a3+6=0,可得﹣2a2a3+6=0,即2(a1+a4)﹣2a2a3+6=0,
a1+a1+3d﹣(a1+d)(a1+2d)+3=0,即﹣1﹣1+3d﹣(﹣1+d)(﹣1+2d)+3=0,
整理可得:d2=3d,解得d=3,
所以Sn=na1+d=﹣n+=,
即Sn=;
(Ⅱ)因为对于每个n∈N*,存在实数cn,使an+cn,an+1+4cn,an+2+15cn成等比数列,
则(a1+nd+4cn)2=[a1+(n﹣1)d+cn][(a1+(n+1)d+15cn],a1=﹣1,
整理可得:cn2+[(14﹣8n)d+8]cn+d2=0,则Δ=[(14﹣8n)d+8]2﹣4d2≥0,
即(7﹣4n)d+4≥d或(7﹣4n)d+4≤﹣d,
整理可得(3﹣2n)d≥﹣2或(2﹣n)d≤﹣1,
当n=1时,可得d≥﹣2或d≤﹣1,而d>1,
所以d≤﹣1(舍),
所以d的范围为(1,+∞);
n=2时,d≤2或 ,而d>1,
所以此时d∈(1,2],
当n为大于2的任何整数,d≤或d≥,而d>1,
所以d≤(舍),d>1恒成立;
综上所述,n=2时,d∈(1,2];
n为不等于2的正整数时,d的取值范围为(1,+∞),都存在cn,使an+cn,an+1+4cn,an+2+15cn成等比数列.
六.三角函数中的恒等变换应用(共1小题)
7.(2021 浙江)设函数f(x)=sinx+cosx(x∈R).
(Ⅰ)求函数y=[f(x+)]2的最小正周期;
(Ⅱ)求函数y=f(x)f(x﹣)在[0,]上的最大值.
【解析】解:函数f(x)=sinx+cosx=,
(Ⅰ)函数y=[f(x+)]2=[2=2cos2(x+)
=1+cos[2(x+)]=1+cos(2x+)=1﹣sin2x,
则最小正周期为T=;
(Ⅱ)函数y=f(x)f(x﹣)=
=sinx+cosx)sinx=
==sin(2x﹣)+,
因为x,所以2x﹣,
所以当2x﹣,即x=时,ymax=1+.
七.正弦定理(共1小题)
8.(2020 浙江)在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知2bsinA﹣a=0.
(Ⅰ)求角B的大小;
(Ⅱ)求cosA+cosB+cosC的取值范围.
【解析】解:(Ⅰ)∵2bsinA=a,
∴2sinBsinA=sinA,
∵sinA≠0,
∴sinB=,
∵△ABC为锐角三角形,
∴B=,
(Ⅱ)∵△ABC为锐角三角形,B=,
∴C=﹣A,
∴cosA+cosB+cosC=cosA+cos(﹣A)+cos=cosA﹣cosA+sinA+=cosA+sinA+=sin(A+)+,
△ABC为锐角三角形,0<A<,0<C<,
解得<A<,
∴<A+<,
∴<sin(A+)≤1,
∴+<sin(A+)+≤,
∴cosA+cosB+cosC的取值范围为(,].
八.三角形中的几何计算(共1小题)
9.(2022 浙江)在△ABC中,角A,B,C所对的边分别为a,b,c.已知4a=c,cosC=.
(Ⅰ)求sinA的值;
(Ⅱ)若b=11,求△ABC的面积.
【解析】解:(Ⅰ)因为cosC=>0,所以C∈(0,),且sinC==,
由正弦定理可得:=,
即有sinA==sinC=×=;
(Ⅱ)因为4a=c a=c<c,
所以A<C,故A∈(0,),
又因为sinA=,所以cosA=,
所以sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC=;
由正弦定理可得:===5,
所以a=5sinA=5,
所以S△ABC=absinC=×5×11×=22.
九.直线与圆锥曲线的综合(共2小题)
10.(2022 浙江)如图,已知椭圆+y2=1.设A,B是椭圆上异于P(0,1)的两点,且点Q(0,)在线段AB上,直线PA,PB分别交直线y=﹣x+3于C,D两点.
(Ⅰ)求点P到椭圆上点的距离的最大值;
(Ⅱ)求|CD|的最小值.
【解析】解:(Ⅰ)设椭圆上任意一点M(x,y),则|PM|2=x2+(y﹣1)2=12﹣12y2+y2﹣2y+1=﹣11y2﹣2y+13,y∈[﹣1,1],
而函数z=﹣11y2﹣2y+13的对称轴为,则其最大值为,
∴,即点P到椭圆上点的距离的最大值为;
(Ⅱ)设直线AB:,
联立直线AB与椭圆方程有,消去y并整理可得,(12k2+1)x2+12kx﹣9=0,
由韦达定理可得,,
∴=,
设C(x3,y3),D(x4,y4),直线AP:,直线BP:,
联立以及,
可得,
∴由弦长公式可得====,当且仅当时等号成立,
∴|CD|的最小值为.
11.(2021 浙江)如图,已知F是抛物线y2=2px(p>0)的焦点,M是抛物线的准线与x轴的交点,且|MF|=2.
(Ⅰ)求抛物线的方程:
(Ⅱ)设过点F的直线交抛物线于A,B两点,若斜率为2的直线l与直线MA,MB,AB,x轴依次交于点P,Q,R,N,且满足|RN|2=|PN| |QN|,求直线l在x轴上截距的取值范围.
【解析】解:(Ⅰ)依题意,p=2,故抛物线的方程为y2=4x;
(Ⅱ)由题意得,直线AB的斜率存在且不为零,设直线AB:y=k(x﹣1),
将直线AB方程代入抛物线方程可得,k2x2﹣(2k2+4)x+k2=0,
则由韦达定理有,,则yAyB=﹣4,
设直线AM:y=k1(x+1),其中,设直线BM:y=k2(x+1),其中,
则===,
,
设直线l:y=2(x﹣t),
联立,可得,则,
联立,可得,则,
同理可得,,
又|RN|2=|PN| |QN|,
∴,即,
∴=(t≠1),
∴4(t2+2t+1)≥3(t2﹣2t+1),即t2+14t+1≥0,解得或(t≠1);
当直线AB的斜率不存在时,则直线AB:x=1,A(1,2),B(1,﹣2),M(﹣1,0),
∴直线MA的方程为y=x+1,直线MB的方程为y=﹣x﹣1,
设直线l:y=2(x﹣t),则P(1+2t,2+2t),,R(1,2﹣2t),N(t,0),
又|RN|2=|PN| |QN|,故,
解得t满足.
∴直线l在x轴上截距的取值范围为.
一十.直线与抛物线的综合(共1小题)
12.(2020 浙江)如图,已知椭圆C1:+y2=1,抛物线C2:y2=2px(p>0),点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C1于点B,交抛物线C2于点M(B,M不同于A).
(Ⅰ)若p=,求抛物线C2的焦点坐标;
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点,求p的最大值.
【解析】解:(Ⅰ)p=,则=,则抛物线C2的焦点坐标(,0),
(Ⅱ)直线l与x轴垂直时,此时点M与点A或点B重合,不满足题意,
设直线l的方程为y=kx+t,A(x1,y1),B(x2,y2),M(x0,y0),
由,消y可得(2k2+1)x2+4ktx+2t2﹣2=0,
∴Δ=16k2t2﹣4(2k2+1)(2t2﹣2)>0,即t2<1+2k2,
∴x1+x2=﹣,∴x0=(x1+x2)=﹣,
∴y0=kx0+t=,∴M(﹣,),
∵点M在抛物线C2上,∴y2=2px,
∴p===,
联立,解得x1=,y1=,
代入椭圆方程可得+=1,解得t2=
∴p2==
=≤=,
∴p≤,当且仅当1=2k2,即k2=,t2=时等号成立,
故p的最大值为.
一十一.直线与平面所成的角(共2小题)
13.(2021 浙江)如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠ABC=120°,AB=1,BC=4,PA=,M,N分别为BC,PC的中点,PD⊥DC,PM⊥MD.
(Ⅰ)证明:AB⊥PM;
(Ⅱ)求直线AN与平面PDM所成角的正弦值.
【解析】(Ⅰ)证明:在平行四边形ABCD中,由已知可得,CD=AB=1,
CM=BC=2,∠DCM=60°,
∴由余弦定理可得,DM2=CD2+CM2﹣2CD×CM×cos60°
=,
则CD2+DM2=1+3=4=CM2,即CD⊥DM,
又PD⊥DC,PD∩DM=D,∴CD⊥平面PDM,
而PM 平面PDM,∴CD⊥PM,
∵CD∥AB,∴AB⊥PM;
(Ⅱ)解:由(Ⅰ)知,CD⊥平面PDM,
又CD 平面ABCD,∴平面ABCD⊥平面PDM,
且平面ABCD∩平面PDM=DM,
∵PM⊥MD,且PM 平面PDM,∴PM⊥平面ABCD,
连接AM,则PM⊥MA,
在△ABM中,AB=1,BM=2,∠ABM=120°,
可得,
又PA=,在Rt△PMA中,求得PM=,
取AD中点E,连接ME,则ME∥CD,可得ME、MD、MP两两互相垂直,
以M为坐标原点,分别以MD、ME、MP为x、y、z轴建立空间直角坐标系,
则A(,2,0),P(0,0,),C(),
又N为PC的中点,∴N(),,
平面PDM的一个法向量为,
设直线AN与平面PDM所成角为θ,
则sinθ=|cos<>|==.
故直线AN与平面PDM所成角的正弦值为.
14.(2020 浙江)如图,在三棱台ABC﹣DEF中,平面ACFD⊥平面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求直线DF与平面DBC所成角的正弦值.
【解析】解:(Ⅰ)证明:作DH⊥AC,且交AC于点H,
∵面ADFC⊥面ABC,DH 面ADFC,∴DH⊥BC,
∴在Rt△DHC中,CH=CD cos45°=CD,
∵DC=2BC,∴CH=CD= 2BC= BC,
∴=,即△BHC是直角三角形,且∠HBC=90°,
∴HB⊥BC,∴BC⊥面DHB,∵BD 面DHB,∴BC⊥BD,
∵在三棱台DEF﹣ABC中,EF∥BC,∴EF⊥DB.
(Ⅱ)设BC=1,则BH=1,HC=,
在Rt△DHC中,DH=,DC=2,
在Rt△DHB中,DB===,
作HG⊥BD于G,∵BC⊥HG,∴HG⊥面BCD,∵GC 面BCD,
∴HG⊥GC,∴△HGC是直角三角形,且∠HGC=90°,
设DF与面DBC所成角为θ,则θ即为CH与面DBC的夹角,
且sinθ=sin∠HCG==,
∵在Rt△DHB中,DH HB=BD HG,
∴HG===,
∴sinθ===.
一十二.二面角的平面角及求法(共1小题)
15.(2022 浙江)如图,已知ABCD和CDEF都是直角梯形,AB∥DC,DC∥EF,AB=5,DC=3,EF=1,∠BAD=∠CDE=60°,二面角F﹣DC﹣B的平面角为60°.设M,N分别为AE,BC的中点.
(Ⅰ)证明:FN⊥AD;
(Ⅱ)求直线BM与平面ADE所成角的正弦值.
【解析】证明:(I)由于CD⊥CB,CD⊥CF,
平面ABCD∩平面CDEF=CD,CF 平面CDEF,CB 平面ABCD,
所以∠FCB为二面角F﹣DC﹣B的平面角,
则∠FCB=60°,CD⊥平面CBF,则CD⊥FN.
又,
则△BCF是等边三角形,则CB⊥FN,
因为DC⊥FC,DC⊥BC,FC∩BC=C,FC 平面FCB,BC 平面FCB,
所以DC⊥平面FCB,因为FN 平面FCB,所以DC⊥FN,
又因为DC∩CB=C,DC 平面ABCD,CB 平面ABCD,
所以FN⊥平面ABCD,因为AD 平面ABCD,故FN⊥AD;
解:(Ⅱ)由于FN⊥平面ABCD,如图建系:
于是,则,
,
设平面ADE的法向量=(x,y,z),
则,∴,令x=,则y=﹣1,z=,
∴平面ADE的法向量,
设BM与平面ADE所成角为θ,
则.
同课章节目录
