03解答题知识点分类-北京市高考数学真题三年(2020-2022)分类汇编(word含答案解析)
文档属性
| 名称 | 03解答题知识点分类-北京市高考数学真题三年(2020-2022)分类汇编(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 720.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:17:45 | ||
图片预览




文档简介
03解答题知识点分类-北京市高考数学真题三年(2020-2022)分类汇编
一.利用导数研究函数的单调性(共1小题)
1.(2022 北京)已知函数f(x)=exln(1+x).
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
二.利用导数研究曲线上某点切线方程(共2小题)
2.(2021 北京)已知函数f(x)=.
(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若f(x)在x=﹣1处取得极值,求f(x)的单调区间,并求其最大值和最小值.
3.(2020 北京)已知函数f(x)=12﹣x2.
(Ⅰ)求曲线y=f(x)的斜率等于﹣2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S (t),求S(t)的最小值.
三.等比数列的性质(共1小题)
4.(2020 北京)已知{an}是无穷数列.给出两个性质:
①对于{an}中任意两项ai,aj(i>j),在{an}中都存在一项am,使得=am;
②对于{an}中任意一项an(n≥3),在{an}中都存在两项ak,al(k>l),使得an=.
(Ⅰ)若an=n(n=1,2,…),判断数列{an}是否满足性质①,说明理由;
(Ⅱ)若an=2n﹣1(n=1,2,…),判断数列{an}是否同时满足性质①和性质②,说明理由;
(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.
四.数列的应用(共2小题)
5.(2022 北京)已知Q:a1,a2,…,ak为有穷整数数列.给定正整数m,若对任意的n∈{1,2,…,m},在Q中存在ai,ai+1,ai+2,…,ai+j(j≥0),使得ai+ai+1+ai+2+…+ai+j=n,则称Q为m﹣连续可表数列.
(Ⅰ)判断Q:2,1,4是否为5﹣连续可表数列?是否为6﹣连续可表数列?说明理由;
(Ⅱ)若Q:a1,a2,…,ak为8﹣连续可表数列,求证:k的最小值为4;
(Ⅲ)若Q:a1,a2,…,ak为20﹣连续可表数列,且a1+a2+…+ak<20,求证:k≥7.
6.(2021 北京)设p为实数.若无穷数列{an}满足如下三个性质,则称{an} 为 p数列:
①a1+p≥0,且a2+p=0;
②a4n﹣1<a4n(n=1,2,…);
③am+n∈{am+an+p,am+an+p+1}(m=1,2,…;n=1,2,…).
(Ⅰ)如果数列{an}的前四项为2,﹣2,﹣2,﹣1,那么{an}是否可能为 2数列?说明理由;
(Ⅱ)若数列{an}是 0数列,求a5;
(Ⅲ)设数列{an}的前n项和为Sn,是否存在 p数列{an},使得Sn≥S10恒成立?如果存在,求出所有的p;如果不存在,说明理由.
五.列举法计算基本事件数及事件发生的概率(共1小题)
7.(2020 北京)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案;方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如表:
男生 女生
支持 不支持 支持 不支持
方案一 200人 400人 300人 100人
方案二 350人 250人 150人 250人
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案二的概率估计值记为p0.假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为p1.试比较p0与p1的大小.(结论不要求证明)
六.离散型随机变量的期望与方差(共2小题)
8.(2022 北京)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(Ⅰ)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(Ⅱ)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望EX;
(Ⅲ)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
9.(2021 北京)在核酸检测中,“k合1”混采核酸检测是指:先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行1次检测,得到每人的检测结果,检测结束.
现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确.
(Ⅰ)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测.
(ⅰ)如果感染新冠病毒的2人在同一组,求检测的总次数:
(ⅱ)已知感染新冠病毒的2人分在同一组的概率为.设X是检测的总次数,求X的分布列与数学期望E(X).
(Ⅱ)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数,试判断数学期望E(Y)与(Ⅰ)中E(X)的大小.(结论不要求证明)
七.正弦定理(共2小题)
10.(2021 北京)在△ABC中,c=2bcosB,∠C=.
(Ⅰ)求∠B;
(Ⅱ)再在条件①、条件②、条件③这三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长.
条件①c=b;
条件②△ABC的周长为4+2;
条件③△ABC的面积为.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
11.(2020 北京)在△ABC中,a+b=11,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)a的值;
(Ⅱ)sinC和△ABC的面积.
条件①:c=7,cosA=﹣;
条件②:cosA=,cosB=.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
八.解三角形(共1小题)
12.(2022 北京)在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
九.直线与椭圆的综合(共3小题)
13.(2022 北京)已知椭圆E:+=1(a>b>0)的一个顶点为A(0,1),焦距为2.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(﹣2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N.当|MN|=2时,求k的值.
14.(2021 北京)已知椭圆E:+=1(a>b>0)的一个顶点A(0,﹣2),以椭圆E的四个顶点围成的四边形面积为4.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(0,﹣3)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB、AC分别与直线y=﹣3交于点M、N,当|PM|+|PN|≤15时,求k的取值范围.
15.(2020 北京)已知椭圆C:+=1过点A(﹣2,﹣1),且a=2b.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(﹣4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x=﹣4于点P,Q.求的值.
一十.直线与平面所成的角(共2小题)
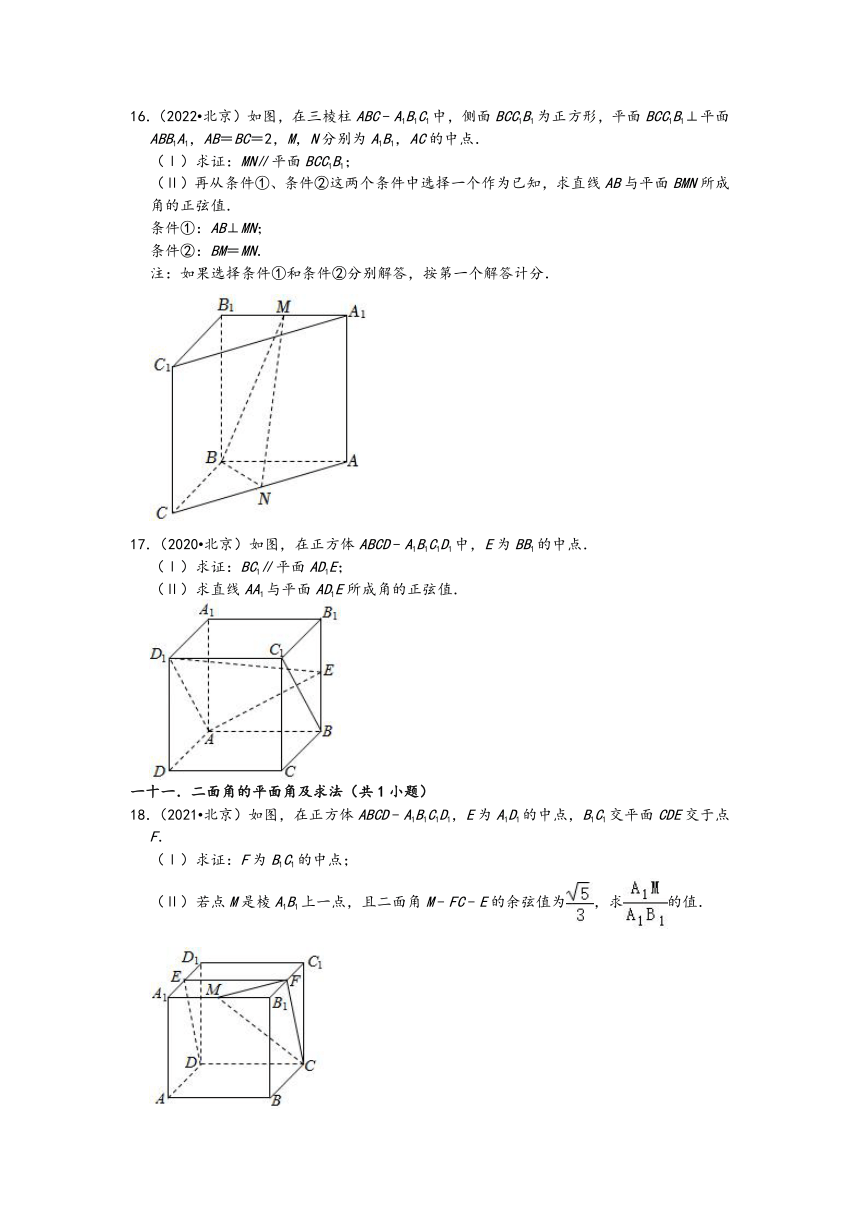
16.(2022 北京)如图,在三棱柱ABC﹣A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(Ⅰ)求证:MN∥平面BCC1B1;
(Ⅱ)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
17.(2020 北京)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(Ⅰ)求证:BC1∥平面AD1E;
(Ⅱ)求直线AA1与平面AD1E所成角的正弦值.
一十一.二面角的平面角及求法(共1小题)
18.(2021 北京)如图,在正方体ABCD﹣A1B1C1D1,E为A1D1的中点,B1C1交平面CDE交于点F.
(Ⅰ)求证:F为B1C1的中点;
(Ⅱ)若点M是棱A1B1上一点,且二面角M﹣FC﹣E的余弦值为,求的值.
参考答案与试题解析
一.利用导数研究函数的单调性(共1小题)
1.(2022 北京)已知函数f(x)=exln(1+x).
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
【解析】解:(Ⅰ)对函数求导可得:,
将x=0代入原函数可得f(0)=0,将x=0代入导函数可得:f′(0)=1,
故在x=0处切线斜率为1,故y﹣0=1(x﹣0),化简得:y=x;
(Ⅱ)由(Ⅰ)有:g(x)=,
,
令,令x+1=k(k≥1),
设,恒成立,
故h(x)在[0,+∞)单调递增,又因为h(0)=1,
故h(x)>0在[0,+∞)恒成立,故g′(x)>0,
故g(x)在[0,+∞)单调递增;
(Ⅲ)证明:由(Ⅱ)有g(x)在[0,+∞)单调递增,又g(0)=1,
故g(x)>0在[0,+∞)恒成立,故f(x)在[0,+∞)单调递增,
设w(x)=f(x+t)﹣f(x),w′(x)=f′(x+t)﹣f′(x),
由(Ⅱ)有g(x)在[0,+∞)单调递增,又因为x+t>x,所以f′(x+t)>f′(x),
故w(x)单调递增,又因为s>0,故w(s)>w(0),
即:f(s+t)﹣f(s)>f(t)﹣f(0),又因为函数f(0)=0,
故f(s+t)>f(s)+f(t),得证.
二.利用导数研究曲线上某点切线方程(共2小题)
2.(2021 北京)已知函数f(x)=.
(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若f(x)在x=﹣1处取得极值,求f(x)的单调区间,并求其最大值和最小值.
【解析】解:(Ⅰ)f(x)=的导数为f′(x)==,
可得y=f(x)在(1,1)处的切线的斜率为﹣4,
则y=f(x)在(1,f(1))处的切线方程为y﹣1=﹣4(x﹣1),
即为y=﹣4x+5;
(Ⅱ)f(x)=的导数为f′(x)==,
由题意可得f′(﹣1)=0,即=0,解得a=4,
可得f(x)=,
f′(x)=,
当x>4或x<﹣1时,f′(x)>0,f(x)递增;当﹣1<x<4时,f′(x)<0,f(x)递减.
函数y=f(x)的图象如右图,当x→﹣∞,y→0;x→+∞,y→0,
则f(x)在x=﹣1处取得极大值1,且为最大值1;在x=4处取得极小值﹣,且为最小值﹣.
所以f(x)的增区间为(﹣∞,﹣1),(4,+∞),减区间为(﹣1,4);
f(x)的最大值为1,最小值为﹣.
3.(2020 北京)已知函数f(x)=12﹣x2.
(Ⅰ)求曲线y=f(x)的斜率等于﹣2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S (t),求S(t)的最小值.
【解析】解:(Ⅰ)f(x)=12﹣x2的导数f′(x)=﹣2x,
令切点为(m,n),可得切线的斜率为﹣2m=﹣2,
∴m=1,∴n=12﹣1=11,
∴切线的方程为y=﹣2x+13;
(Ⅱ)曲线y=f(x)在点(t,f(t))处的切线的斜率为k=﹣2t,
切线方程为y﹣(12﹣t2)=﹣2t(x﹣t),
令x=0,可得y=12+t2,令y=0,可得x=t+,
∴S (t)= |t+| (12+t2),
由S(﹣t)=S(t),可知S(t)为偶函数,
不妨设t>0,则S(t)=(t+)(12+t2),
∴S′(t)=(3t2+24﹣)= ,
由S′(t)=0,得t=2,
当t>2时,S′(t)>0,S(t)递增;当0<t<2时,S′(t)<0,S(t)递减,
则S(t)在t=2处取得极小值,且为最小值32,
同理可得t<0时,S(t)在t=﹣2处取得极小值,且为最小值32,
所以S(t)的最小值为32.
三.等比数列的性质(共1小题)
4.(2020 北京)已知{an}是无穷数列.给出两个性质:
①对于{an}中任意两项ai,aj(i>j),在{an}中都存在一项am,使得=am;
②对于{an}中任意一项an(n≥3),在{an}中都存在两项ak,al(k>l),使得an=.
(Ⅰ)若an=n(n=1,2,…),判断数列{an}是否满足性质①,说明理由;
(Ⅱ)若an=2n﹣1(n=1,2,…),判断数列{an}是否同时满足性质①和性质②,说明理由;
(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.
【解析】解:(Ⅰ)不满足,理由:= N*,不存在一项am使得=am.
(Ⅱ)数列{an}同时满足性质①和性质②,
理由:对于任意的i和j,满足=22i﹣j﹣1,因为i∈N*,j∈N*且i>j,所以2i﹣j∈N*,则必存在m=2i﹣j,此时,2m﹣1∈{ai}且满足=22i﹣j﹣1=am,性质①成立,
对于任意的n,欲满足an=2n﹣1==22k﹣l﹣1,满足n=2k﹣l即可,因为k∈N*,l∈N*,且k>l,
所以2k﹣l可表示所有正整数,所以必有一组k,l使n=2k﹣l,即满足an=,性质②成立.
(Ⅲ)首先,先证明数列恒正或恒负,
反证法:假设这个递增数列先负后正,
那么必有一项al绝对值最小或者有al与al+1同时取得绝对值最小,
如仅有一项al绝对值最小,此时必有一项am=,此时|am|<|al|
与前提矛盾,
如有两项al与al+1 同时取得绝对值最小值,那么必有am=,
此时|am|=|al|,与前提条件矛盾,
所以数列必然恒正或恒负,
在数列恒正的情况下,由②知,存在k,l且k>l,
因为是递增数列,ak>al>0,使得=a3>ak,
即3>k>l,所以=a3,此时a1,a2,a3成等比数列,
数学归纳法:
(1)已证n=3时,满足{an}是等比数列,公比q=,
(2)假设n=k时,也满足{ak}是等比数列,公比q=,
那么由①知=qak等于数列的某一项am,证明这一项为ak+1即可,
反证法:
假设这一项不是ak+1,因为是递增数列,所以该项am==qak>ak+1,
那么ak<ak+1<qak,由等比数列{ak}得a1qk﹣1<ak+1<a1qk,
由性质②得a1qk﹣1<<a1qk,同时ak+1=>am>al,s所以k+1>m>l,
所以am,al分别是等比数列{ak}中两项,即am=a1qm﹣1,al=a1ql﹣1,
原式变为a1qk﹣1<a1q2m﹣l﹣1<a1qk,
所以k﹣1<2m﹣l﹣1<k,又因为k∈N*,m∈N*,l∈N*,不存在这组解,所以矛盾,
所以知=qak=ak+1,{ak+1}为等比数列,
由数学归纳法知,{an}是等比数列得证,
同理,数列恒负,{an}也是等比数列.
四.数列的应用(共2小题)
5.(2022 北京)已知Q:a1,a2,…,ak为有穷整数数列.给定正整数m,若对任意的n∈{1,2,…,m},在Q中存在ai,ai+1,ai+2,…,ai+j(j≥0),使得ai+ai+1+ai+2+…+ai+j=n,则称Q为m﹣连续可表数列.
(Ⅰ)判断Q:2,1,4是否为5﹣连续可表数列?是否为6﹣连续可表数列?说明理由;
(Ⅱ)若Q:a1,a2,…,ak为8﹣连续可表数列,求证:k的最小值为4;
(Ⅲ)若Q:a1,a2,…,ak为20﹣连续可表数列,且a1+a2+…+ak<20,求证:k≥7.
【解析】解:(Ⅰ)若m=5,则对于任意的n∈{1,2,3,4,5},
a2=1,a1=2,a1+a2=2+1=3,a3=4,a2+a3=1+4=5,
所以Q是5﹣连续可表数列;
由于不存在任意连续若干项之和相加为6,
所以Q不是6﹣连续可表数列;
(Ⅱ)假设k的值为3,则a1,a2,a3 最多能表示a1,a2,a3,a1+a2,a2+a3,a1+a2+a3,共6个数字,
与Q是8﹣连续可表数列矛盾,故k≥4;
现构造Q:1,2,3,4可以表达出1,2,3,4,5,6,7,8这8个数字,即存在k=4满足题意.
故k的最小值为4.
(Ⅲ)先证明k≥6.
从5个正整数中,取一个数字只能表示自身,最多可表示5个数字,
取连续两个数字最多能表示4个数字,取连续三个数字最多能表示3个数字,
取连续四个数字最多能表示2个数字,取连续五个数字最多能表示1个数字,
所以对任意给定的5个整数,最多可以表示5+4+3+2+1=15个正整数,不能表示20个正整数,即k≥6.
若k=6,最多可以表示6+5+4+3+2+1=21个正整数,
由于Q为20﹣连续可表数列,且a1+a2+…+ak<20,
所以其中必有一项为负数.
既然5个正整数都不能连续可表1﹣20的正整数,
所以至少要有6个正整数连续可表1﹣20的正整数,
所以至少6个正整数和一个负数才能满足题意,
这是不可能成立的,故k≠6.
故k≥7.
6.(2021 北京)设p为实数.若无穷数列{an}满足如下三个性质,则称{an} 为 p数列:
①a1+p≥0,且a2+p=0;
②a4n﹣1<a4n(n=1,2,…);
③am+n∈{am+an+p,am+an+p+1}(m=1,2,…;n=1,2,…).
(Ⅰ)如果数列{an}的前四项为2,﹣2,﹣2,﹣1,那么{an}是否可能为 2数列?说明理由;
(Ⅱ)若数列{an}是 0数列,求a5;
(Ⅲ)设数列{an}的前n项和为Sn,是否存在 p数列{an},使得Sn≥S10恒成立?如果存在,求出所有的p;如果不存在,说明理由.
【解析】解:(Ⅰ)数列{an}不可能为 2数列,理由如下,
因为p=2,a1=2,a2=﹣2,所以a1+a2+p=2,a1+a2+p+1=3,
因为a3=﹣2,所以a3 {a1+a2+p,a1+a2+p+1},
所以数列{an}不满足性质③.
(Ⅱ)性质①,a1≥0,a2=0;
由性质③am+2∈{am,am+1},因此a3=a1或a3=a1+1,a4=0或a4=1,
若a4=0,由性质②可得a3<a4,即a1<0或a1+1<0,矛盾;
若a4=1,a3=a1+1,由a3<a4,则a1+1<1,矛盾,
因此只能是a4=1,a3=a1,
又因为a4=a1+a3或a4=a1+a3+1,所以a1=或a1=0.
若a1=,则a2∈{a1+a1+0,a1+a1+0+1}={2a1,2a1+1}={1,2},不满足a2=0,舍去;
当a1=0,则{an}的前四项为0,0,0,1,
下面用数学归纳法证明a4n+i=n(i=1,2,3),a4n+4=n+1(n∈N),
当n=0时,经检验命题成立;
假设n≤k(k≥0)时命题成立.
当n=k+1时,
若i=1,则a4(k+1)+1=a4k+5=aj+(4k+5﹣j),
利用性质③:{aj+a4k+5﹣j|j∈N*,1≤j≤4k+4}={k,k+1},此时可得a4k+5=k+1,
否则a4k+5=k,取k=0可得a5=0,而由性质②可得a5=a1+a4∈{1,2},与a5=0矛盾.
同理可得,{aj+a4k+6﹣j|j∈N*,1≤j≤4k+5}={k,k+1},此时可得a4k+6=k+1,
{aj+a4k+8﹣j|j∈N*,2≤j≤4k+6}={k+1,k+2},此时可得a4k+8=k+2,
{aj+a4k+7﹣j|j∈N*,1≤j≤4k+6}={k+1},又因为a4k+7<a4k+8,此时可得a4k+7=k+1,
即当n=k+1时,命题成立.
综上可得,a5=a4×1+1=1;
(Ⅲ)令bn=an+p,由性质③可知, m,n∈N*,bm+n=am+n+p∈{am+p+an+p,am+p+an+p+1}={bm+bn,bm+bn+1},
由于b1=a1+p≥0,b2=a2+p=0,b4n﹣1=a4n﹣1+p<a4n+p=b4n,
因此数列{bn}为 0数列,
由(Ⅱ)可知,若 n∈N*,a4n+i=n﹣p(i=1,2,3),a4n+1=n+1﹣p;
S11﹣S10=a11=a4×2+3=2﹣p≥0,
S9﹣S10=﹣a10=﹣a4×2+2=﹣(2﹣p)≥0,
因此p=2,此时a1,a2, ,a10≤0,aj≥0(j≥11),满足题意.
五.列举法计算基本事件数及事件发生的概率(共1小题)
7.(2020 北京)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案;方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如表:
男生 女生
支持 不支持 支持 不支持
方案一 200人 400人 300人 100人
方案二 350人 250人 150人 250人
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案二的概率估计值记为p0.假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为p1.试比较p0与p1的大小.(结论不要求证明)
【解析】解:(Ⅰ)设“该校男生支持方案一”为事件A,“该校女生支持方案一”为事件B,
则;
(Ⅱ)由(Ⅰ)知,,
设“这3人中恰有2人支持方案一”为事件C,
则;
(Ⅲ)p0>p1.理由如下:
,设该校总人数为a,则该校支持方案二的人数约为,
由表可知,男生支持方案二的概率为,女生支持方案二的概率为,
所以一年级支持方案二的人数约为,
故除一年级外其他年级支持方案二的概率为.
六.离散型随机变量的期望与方差(共2小题)
8.(2022 北京)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(Ⅰ)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(Ⅱ)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望EX;
(Ⅲ)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
【解析】解:(Ⅰ)甲以往的10次成绩中有4次获得优秀奖,用频率估计概率,则甲在校运动会铅球比赛中获得优秀奖的概率=.
(Ⅱ)用频率估计概率,则乙在校运动会铅球比赛中获得优秀奖的概率为=,丙在校运动会铅球比赛中获得优秀奖的概率为=,
X的所有可能取值为0,1,2,3,
则P(X=0)==,
P(X=1)===,
P(X=2)==,
P(X=3)===,
∴EX=0×=.
(Ⅲ)丙获得冠军的概率估计值最大.
9.(2021 北京)在核酸检测中,“k合1”混采核酸检测是指:先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行1次检测,得到每人的检测结果,检测结束.
现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确.
(Ⅰ)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测.
(ⅰ)如果感染新冠病毒的2人在同一组,求检测的总次数:
(ⅱ)已知感染新冠病毒的2人分在同一组的概率为.设X是检测的总次数,求X的分布列与数学期望E(X).
(Ⅱ)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数,试判断数学期望E(Y)与(Ⅰ)中E(X)的大小.(结论不要求证明)
【解析】解:(Ⅰ)(ⅰ)若采用“10合1检测法”,每组检查一次,共10次;
又两名患者在同一组,需要再检查10次,
因此一共需要检查20次.
(ⅱ)由题意可得:X=20,30.
P(X=20)=,P(X=30)=.
可得分布列:
X 20 30
P
E(X)=20×+30×=.
(Ⅱ)由题意可得:Y=25,30.
P(Y=25)=20×=,P(Y=30)=.
可得分布列:
Y 25 30
P
E(Y)=25×+30×=>=.
E(X)<E(Y).
另解:设“10合1”混采核酸检测两名感染患者在同一组的概率为p1,“5合1”混采核酸检测两名感染患者在同一组的概率为p2,则p1>p2,
此时有E(X)=20p1+30(1﹣p1)=30﹣10p1;
而E(Y)=25p2+30(1﹣p2)=30﹣5p2>30﹣5p1>30﹣10p1=E(X),
∴E(X)<E(Y).
七.正弦定理(共2小题)
10.(2021 北京)在△ABC中,c=2bcosB,∠C=.
(Ⅰ)求∠B;
(Ⅱ)再在条件①、条件②、条件③这三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长.
条件①c=b;
条件②△ABC的周长为4+2;
条件③△ABC的面积为.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
【解析】解:(Ⅰ)∵c=2bcosB,
由正弦定理可得sinC=2sinBcosB,即sinC=sin2B,
∵C=,
∴当C=2B 时,B=,即C+B=π,不符合题意,舍去,
∴C+2B=π,
∴2B=,
即B=.
(Ⅱ)选①c=b,
由正弦定理可得
,与已知条件c=b矛盾,故△ABC不存在,
选②周长为4+2,
∵C=,B=,
∴,
由正弦定理可得,即,
∴,
∴a+b+c=(2+)R=4+2,
∴R=2,即a=2,b=2,c=2,
∴△ABC存在且唯一确定,
设BC的中点为D,
∴CD=1,
在△ACD中,运用余弦定理,AD2=AC2+CD2﹣2AC CD cos∠C,
即,AD=,
∴BC边上的中线的长度.
选③面积为S△ABC=,
∵,
∴a=b,
∴,解得a=,
余弦定理可得
AD2=AC2+CD2﹣2×AC×CD×=,
.
11.(2020 北京)在△ABC中,a+b=11,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)a的值;
(Ⅱ)sinC和△ABC的面积.
条件①:c=7,cosA=﹣;
条件②:cosA=,cosB=.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解析】解:选择条件①(Ⅰ)由余弦定理得a2=b2+c2﹣2bccosA,即a2﹣b2=49﹣14b×(﹣)=49+2b,
∴(a+b)(a﹣b)=49+2b,
∵a+b=11,
∴11a﹣11b=49+2b,
即11a﹣13b=49,
联立,解得a=8,b=3,
故a=8.
(Ⅱ)在△ABC中,sinA>0,
∴sinA==,
由正弦定理可得=,
∴sinC===,
∴S△ABC=absinC=×8×3×=6.
选择条件②(Ⅰ)在△ABC中,sinA>0,sinB>0,C=π﹣(A+B),
∵cosA=,cosB=,
∴sinA==,sinB==,
由正弦定理可得=,
∴==,
∵a+b=11,
∴a=6,b=5,
故a=6;
(Ⅱ)在△ABC中,C=π﹣(A+B),
∴sinC=sin(A+B)=sinAcosB+cosAsinB=×+×=,
∴S△ABC=absinC=×6×5×=
八.解三角形(共1小题)
12.(2022 北京)在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
【解析】解:(Ⅰ)∵sin2C=sinC,
∴2sinCcosC=sinC,
又sinC≠0,∴2cosC=,
∴cosC=,∵0<C<π,
∴C=;
(Ⅱ)∵△ABC的面积为6,
∴absinC=6,
又b=6,C=,
∴×a×6×=6,
∴a=4,
又cosC=,
∴=,
∴c=2,
∴a+b+c=6+6,
∴△ABC的周长为6+6.
九.直线与椭圆的综合(共3小题)
13.(2022 北京)已知椭圆E:+=1(a>b>0)的一个顶点为A(0,1),焦距为2.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(﹣2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N.当|MN|=2时,求k的值.
【解析】解:(Ⅰ)由题意得,
,∴b=1,c=,a=2,
∴椭圆E的方程为+y2=1.
(Ⅱ)设过点P(﹣2,1)的直线为y﹣1=k(x+2),B(x1,y1),C(x2,y2),
联立得,即(1+4k2)x2+(16k2+8k)x+16k2+16k=0,
∵直线与椭圆相交,∴Δ=[(16k2+8k)]2﹣4(1+4k2)(16k2+16k)>0,∴k<0,
由韦达定理得x1+x2=﹣,x1 x2=,
∵kAB=,∴直线AB为y=x+1,
令y=0,则x=,∴M(,0),同理N(,0),
∴|MN|=|﹣|=|﹣|=|(﹣)|
=| |=| |
=||=2,
∴| |=2,∴||=,
∴k=﹣4.
14.(2021 北京)已知椭圆E:+=1(a>b>0)的一个顶点A(0,﹣2),以椭圆E的四个顶点围成的四边形面积为4.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(0,﹣3)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB、AC分别与直线y=﹣3交于点M、N,当|PM|+|PN|≤15时,求k的取值范围.
【解析】解:(Ⅰ)因为椭圆E:+=1(a>b>0)过点A(0,﹣2),则b=2,
又因为以四个顶点围成的四边形面积为4,
所以,解得a=,
故椭圆E的标准方程为;
(Ⅱ)由题意,设过点P(0,﹣3),斜率为k的直线为直线l,
设直线l的方程为y﹣(﹣3)=k(x﹣0),即y=kx﹣3,
当k=0时,直线l与椭圆E没有交点,而直线l交椭圆E于不同的两点B,C,
所以k≠0,
设B(x1,y1),C(x2,y2),
联立方程组,可得(4+5k2)x2﹣30kx+25=0,
则Δ=(﹣30k)2﹣4×25(4+5k2)>0,解得|k|>1,
所以,
则y1y2=(kx1﹣3)(kx2﹣3)=k2x1x2﹣3k(x1+x2)+9=,
y1+y2=(kx1﹣3)+(kx2﹣3)=k(x1+x2)﹣6=,
直线AB的方程为y﹣(﹣2)=,即,
直线AC的方程为y﹣(﹣2)=,即,
因为直线AB交y=﹣3于点M,
所以令y=﹣3,则,
故,
同理可得,
注意到>0,所以x1,x2同号,
因为y1+2>0,y2+2>0,所以xM,xN同号,
故|PM|+|PN|=|xM|+|xN|=|xM+xN|,
则|PM|+|PN|==
=
=
=
=5|k|,
故|PM|+|PN|=5|k|,
又|PM|+|PN|≤15,即5|k|≤15,即|k|≤3,又|k|>1,
所以1<|k|≤3,
故k的取值范围为[﹣3,﹣1)∪(1,3].
15.(2020 北京)已知椭圆C:+=1过点A(﹣2,﹣1),且a=2b.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(﹣4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x=﹣4于点P,Q.求的值.
【解析】解:(Ⅰ)椭圆C:+=1过点A(﹣2,﹣1),且a=2b,
则,解得b2=2,a2=8,
∴椭圆方程为+=1,
(Ⅱ)由题意可得直线l的斜率存在,设直线方程为y=k(x+4),
由,
消y整理可得(1+4k2)x2+32k2x+64k2﹣8=0,
∴Δ=﹣32(4k2﹣1)>0,
解得﹣<k<,
设M(x1,y1),N(x2,y2),
∴x1+x2=﹣,x1x2=,
则直线AM的方程为y+1=(x+2),直线AN的方程为y+1=(x+2),
分别令x=﹣4,
可得yP=﹣1=﹣,yQ=﹣
∴|PB|=|yP|=||,|QB|=|yQ|=||,
∴=||=||
∵(2k+1)x1x2+(4k+2)(x1+x2)+8(2k+1)=,
∴||=||=||=1,
故=1.
一十.直线与平面所成的角(共2小题)
16.(2022 北京)如图,在三棱柱ABC﹣A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(Ⅰ)求证:MN∥平面BCC1B1;
(Ⅱ)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解析】解:(I)证明:取AB中点K,连接NK,MK,
∵M,为A1B1的中点.∴B1M∥BK,且B1M∥BK,
∴四边形BKMB1是平行四边形,故MK∥BB1,
MK 平面BCC1B1;BB1 平面BCC1B1,
∴MK∥平面BCC1B1,
∵K是AB中点,N是AC的点,
∴NK∥BC,∵NK 平面BCC1B1;BC 平面BCC1B1,
∴NK∥平面BCC1B1,又NK∩MK=K,
∴平面NMK∥平面BCC1B1,
又MN 平面NMK,∴MN∥平面BCC1B1;
(II)∵侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,
∴CB⊥平面ABB1A1,∴CB⊥AB,又NK∥BC,∴AB⊥NK,
若选①:AB⊥MN;又MN∩NK=N,∴AB⊥平面MNK,
又MK 平面MNK,∴AB⊥MK,又MK∥BB1,
∴AB⊥BB1,∴BC,BA,BB1两两垂直,
若选②:∵CB⊥平面ABB1A1,NK∥BC,∴NK⊥平面ABB1A1,KM 平面ABB1A1,
∴MK⊥NK,又BM=MN,NK=BC,BK=AB,
∴△BKM≌△NKM,∴∠BKM=∠NKM=90°,
∴AB⊥MK,又MK∥BB1,∴AB⊥BB1,
∴BC,BA,BB1两两垂直,
以B为坐标原点,BC,BA,BB1为坐标轴建立如图所示的空间直角坐标系,
则B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),
∴=(0,1,2),=(1,1,0),
设平面BMN的一个法向量为=(x,y,z),
则,令z=1,则y=﹣2,x=2,
∴平面BMN的一个法向量为=(2,﹣2,1),
又=(0,2,0),
设直线AB与平面BMN所成角为θ,
∴sinθ=|cos<,>|===.
∴直线AB与平面BMN所成角的正弦值为.
17.(2020 北京)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(Ⅰ)求证:BC1∥平面AD1E;
(Ⅱ)求直线AA1与平面AD1E所成角的正弦值.
【解析】解:(Ⅰ)由正方体的性质可知,AB∥C1D1中,且AB=C1D1,
∴四边形ABC1D1是平行四边形,∴BC1∥AD1,
又BC1 平面AD1E,AD1 平面AD1E,∴BC1∥平面AD1E.
(Ⅱ)解法一:以A为原点,AD、AB、AA1分别为x、y和z轴建立如图所示的空间直角坐标系,
设正方体的棱长为a,则A(0,0,0),A1(0,0,a),D1(a,0,a),E(0,a,a),
∴,,,
设平面AD1E的法向量为,则,即,
令z=2,则x=﹣2,y=﹣1,∴=(﹣2,﹣1,2),
设直线AA1与平面AD1E所成角为θ,则sinθ=|cos<,>|==,
故直线AA1与平面AD1E所成角的正弦值为.
解法二:设正方体的棱长为2a,则AD1=a,AE=a,ED1=3a,= 2a 2a=2a2,
由余弦定理知,cos∠EAD1===,
∴sin∠EAD1=,
∴=AD1 AE sin∠EAD1=3a2,
设点A1到平面EAD1的距离为h,
∵=,
∴,∴h=,
设直线AA1与平面AD1E所成角为θ,则sinθ==.
故直线AA1与平面AD1E所成角的正弦值为.
一十一.二面角的平面角及求法(共1小题)
18.(2021 北京)如图,在正方体ABCD﹣A1B1C1D1,E为A1D1的中点,B1C1交平面CDE交于点F.
(Ⅰ)求证:F为B1C1的中点;
(Ⅱ)若点M是棱A1B1上一点,且二面角M﹣FC﹣E的余弦值为,求的值.
【解析】(Ⅰ)证明:连结DE,
在正方体ABCD﹣A1B1C1D1中,CD∥C1D1,C1D1 平面A1B1C1D1,CD 平面A1B1C1D1,
则CD∥平面A1B1C1D1,因为平面A1B1C1D1∩平面CDEF=EF,
所以CD∥EF,则EF∥C1D1,
故A1B1∥EF∥C1D1,又因为A1D1∥B1C1,
所以四边形A1B1FE为平行四边形,四边形EFC1D1为平行四边形,
所以A1E=B1F,ED1=FC1,
而点E为A1D1的中点,所以A1E=ED1,
故B1F=FC1,则点F为B1C1的中点;
(Ⅱ)解:以点B1为原点,建立空间直角坐标系,如图所示,
设正方体棱长为2,设点M(m,0,0),
因为二面角M﹣FC﹣E的余弦值为,则m<0,所以m≠0,
则C(0,2,﹣2),E(﹣2,1,0),F(0,1,0),
故,
设平面CMF的法向量为,
则,即,
所以,b=2,故,
设平面CDEF的法向量为,
则,即,
所以x=0,y=2,故,
因为二面角M﹣FC﹣E的余弦值为,
则==,
解得m=±1,又m<0,
所以m=﹣1,
故=.
一.利用导数研究函数的单调性(共1小题)
1.(2022 北京)已知函数f(x)=exln(1+x).
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
二.利用导数研究曲线上某点切线方程(共2小题)
2.(2021 北京)已知函数f(x)=.
(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若f(x)在x=﹣1处取得极值,求f(x)的单调区间,并求其最大值和最小值.
3.(2020 北京)已知函数f(x)=12﹣x2.
(Ⅰ)求曲线y=f(x)的斜率等于﹣2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S (t),求S(t)的最小值.
三.等比数列的性质(共1小题)
4.(2020 北京)已知{an}是无穷数列.给出两个性质:
①对于{an}中任意两项ai,aj(i>j),在{an}中都存在一项am,使得=am;
②对于{an}中任意一项an(n≥3),在{an}中都存在两项ak,al(k>l),使得an=.
(Ⅰ)若an=n(n=1,2,…),判断数列{an}是否满足性质①,说明理由;
(Ⅱ)若an=2n﹣1(n=1,2,…),判断数列{an}是否同时满足性质①和性质②,说明理由;
(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.
四.数列的应用(共2小题)
5.(2022 北京)已知Q:a1,a2,…,ak为有穷整数数列.给定正整数m,若对任意的n∈{1,2,…,m},在Q中存在ai,ai+1,ai+2,…,ai+j(j≥0),使得ai+ai+1+ai+2+…+ai+j=n,则称Q为m﹣连续可表数列.
(Ⅰ)判断Q:2,1,4是否为5﹣连续可表数列?是否为6﹣连续可表数列?说明理由;
(Ⅱ)若Q:a1,a2,…,ak为8﹣连续可表数列,求证:k的最小值为4;
(Ⅲ)若Q:a1,a2,…,ak为20﹣连续可表数列,且a1+a2+…+ak<20,求证:k≥7.
6.(2021 北京)设p为实数.若无穷数列{an}满足如下三个性质,则称{an} 为 p数列:
①a1+p≥0,且a2+p=0;
②a4n﹣1<a4n(n=1,2,…);
③am+n∈{am+an+p,am+an+p+1}(m=1,2,…;n=1,2,…).
(Ⅰ)如果数列{an}的前四项为2,﹣2,﹣2,﹣1,那么{an}是否可能为 2数列?说明理由;
(Ⅱ)若数列{an}是 0数列,求a5;
(Ⅲ)设数列{an}的前n项和为Sn,是否存在 p数列{an},使得Sn≥S10恒成立?如果存在,求出所有的p;如果不存在,说明理由.
五.列举法计算基本事件数及事件发生的概率(共1小题)
7.(2020 北京)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案;方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如表:
男生 女生
支持 不支持 支持 不支持
方案一 200人 400人 300人 100人
方案二 350人 250人 150人 250人
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案二的概率估计值记为p0.假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为p1.试比较p0与p1的大小.(结论不要求证明)
六.离散型随机变量的期望与方差(共2小题)
8.(2022 北京)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(Ⅰ)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(Ⅱ)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望EX;
(Ⅲ)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
9.(2021 北京)在核酸检测中,“k合1”混采核酸检测是指:先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行1次检测,得到每人的检测结果,检测结束.
现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确.
(Ⅰ)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测.
(ⅰ)如果感染新冠病毒的2人在同一组,求检测的总次数:
(ⅱ)已知感染新冠病毒的2人分在同一组的概率为.设X是检测的总次数,求X的分布列与数学期望E(X).
(Ⅱ)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数,试判断数学期望E(Y)与(Ⅰ)中E(X)的大小.(结论不要求证明)
七.正弦定理(共2小题)
10.(2021 北京)在△ABC中,c=2bcosB,∠C=.
(Ⅰ)求∠B;
(Ⅱ)再在条件①、条件②、条件③这三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长.
条件①c=b;
条件②△ABC的周长为4+2;
条件③△ABC的面积为.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
11.(2020 北京)在△ABC中,a+b=11,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)a的值;
(Ⅱ)sinC和△ABC的面积.
条件①:c=7,cosA=﹣;
条件②:cosA=,cosB=.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
八.解三角形(共1小题)
12.(2022 北京)在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
九.直线与椭圆的综合(共3小题)
13.(2022 北京)已知椭圆E:+=1(a>b>0)的一个顶点为A(0,1),焦距为2.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(﹣2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N.当|MN|=2时,求k的值.
14.(2021 北京)已知椭圆E:+=1(a>b>0)的一个顶点A(0,﹣2),以椭圆E的四个顶点围成的四边形面积为4.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(0,﹣3)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB、AC分别与直线y=﹣3交于点M、N,当|PM|+|PN|≤15时,求k的取值范围.
15.(2020 北京)已知椭圆C:+=1过点A(﹣2,﹣1),且a=2b.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(﹣4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x=﹣4于点P,Q.求的值.
一十.直线与平面所成的角(共2小题)
16.(2022 北京)如图,在三棱柱ABC﹣A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(Ⅰ)求证:MN∥平面BCC1B1;
(Ⅱ)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
17.(2020 北京)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(Ⅰ)求证:BC1∥平面AD1E;
(Ⅱ)求直线AA1与平面AD1E所成角的正弦值.
一十一.二面角的平面角及求法(共1小题)
18.(2021 北京)如图,在正方体ABCD﹣A1B1C1D1,E为A1D1的中点,B1C1交平面CDE交于点F.
(Ⅰ)求证:F为B1C1的中点;
(Ⅱ)若点M是棱A1B1上一点,且二面角M﹣FC﹣E的余弦值为,求的值.
参考答案与试题解析
一.利用导数研究函数的单调性(共1小题)
1.(2022 北京)已知函数f(x)=exln(1+x).
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).
【解析】解:(Ⅰ)对函数求导可得:,
将x=0代入原函数可得f(0)=0,将x=0代入导函数可得:f′(0)=1,
故在x=0处切线斜率为1,故y﹣0=1(x﹣0),化简得:y=x;
(Ⅱ)由(Ⅰ)有:g(x)=,
,
令,令x+1=k(k≥1),
设,恒成立,
故h(x)在[0,+∞)单调递增,又因为h(0)=1,
故h(x)>0在[0,+∞)恒成立,故g′(x)>0,
故g(x)在[0,+∞)单调递增;
(Ⅲ)证明:由(Ⅱ)有g(x)在[0,+∞)单调递增,又g(0)=1,
故g(x)>0在[0,+∞)恒成立,故f(x)在[0,+∞)单调递增,
设w(x)=f(x+t)﹣f(x),w′(x)=f′(x+t)﹣f′(x),
由(Ⅱ)有g(x)在[0,+∞)单调递增,又因为x+t>x,所以f′(x+t)>f′(x),
故w(x)单调递增,又因为s>0,故w(s)>w(0),
即:f(s+t)﹣f(s)>f(t)﹣f(0),又因为函数f(0)=0,
故f(s+t)>f(s)+f(t),得证.
二.利用导数研究曲线上某点切线方程(共2小题)
2.(2021 北京)已知函数f(x)=.
(Ⅰ)若a=0,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若f(x)在x=﹣1处取得极值,求f(x)的单调区间,并求其最大值和最小值.
【解析】解:(Ⅰ)f(x)=的导数为f′(x)==,
可得y=f(x)在(1,1)处的切线的斜率为﹣4,
则y=f(x)在(1,f(1))处的切线方程为y﹣1=﹣4(x﹣1),
即为y=﹣4x+5;
(Ⅱ)f(x)=的导数为f′(x)==,
由题意可得f′(﹣1)=0,即=0,解得a=4,
可得f(x)=,
f′(x)=,
当x>4或x<﹣1时,f′(x)>0,f(x)递增;当﹣1<x<4时,f′(x)<0,f(x)递减.
函数y=f(x)的图象如右图,当x→﹣∞,y→0;x→+∞,y→0,
则f(x)在x=﹣1处取得极大值1,且为最大值1;在x=4处取得极小值﹣,且为最小值﹣.
所以f(x)的增区间为(﹣∞,﹣1),(4,+∞),减区间为(﹣1,4);
f(x)的最大值为1,最小值为﹣.
3.(2020 北京)已知函数f(x)=12﹣x2.
(Ⅰ)求曲线y=f(x)的斜率等于﹣2的切线方程;
(Ⅱ)设曲线y=f(x)在点(t,f(t))处的切线与坐标轴围成的三角形的面积为S (t),求S(t)的最小值.
【解析】解:(Ⅰ)f(x)=12﹣x2的导数f′(x)=﹣2x,
令切点为(m,n),可得切线的斜率为﹣2m=﹣2,
∴m=1,∴n=12﹣1=11,
∴切线的方程为y=﹣2x+13;
(Ⅱ)曲线y=f(x)在点(t,f(t))处的切线的斜率为k=﹣2t,
切线方程为y﹣(12﹣t2)=﹣2t(x﹣t),
令x=0,可得y=12+t2,令y=0,可得x=t+,
∴S (t)= |t+| (12+t2),
由S(﹣t)=S(t),可知S(t)为偶函数,
不妨设t>0,则S(t)=(t+)(12+t2),
∴S′(t)=(3t2+24﹣)= ,
由S′(t)=0,得t=2,
当t>2时,S′(t)>0,S(t)递增;当0<t<2时,S′(t)<0,S(t)递减,
则S(t)在t=2处取得极小值,且为最小值32,
同理可得t<0时,S(t)在t=﹣2处取得极小值,且为最小值32,
所以S(t)的最小值为32.
三.等比数列的性质(共1小题)
4.(2020 北京)已知{an}是无穷数列.给出两个性质:
①对于{an}中任意两项ai,aj(i>j),在{an}中都存在一项am,使得=am;
②对于{an}中任意一项an(n≥3),在{an}中都存在两项ak,al(k>l),使得an=.
(Ⅰ)若an=n(n=1,2,…),判断数列{an}是否满足性质①,说明理由;
(Ⅱ)若an=2n﹣1(n=1,2,…),判断数列{an}是否同时满足性质①和性质②,说明理由;
(Ⅲ)若{an}是递增数列,且同时满足性质①和性质②,证明:{an}为等比数列.
【解析】解:(Ⅰ)不满足,理由:= N*,不存在一项am使得=am.
(Ⅱ)数列{an}同时满足性质①和性质②,
理由:对于任意的i和j,满足=22i﹣j﹣1,因为i∈N*,j∈N*且i>j,所以2i﹣j∈N*,则必存在m=2i﹣j,此时,2m﹣1∈{ai}且满足=22i﹣j﹣1=am,性质①成立,
对于任意的n,欲满足an=2n﹣1==22k﹣l﹣1,满足n=2k﹣l即可,因为k∈N*,l∈N*,且k>l,
所以2k﹣l可表示所有正整数,所以必有一组k,l使n=2k﹣l,即满足an=,性质②成立.
(Ⅲ)首先,先证明数列恒正或恒负,
反证法:假设这个递增数列先负后正,
那么必有一项al绝对值最小或者有al与al+1同时取得绝对值最小,
如仅有一项al绝对值最小,此时必有一项am=,此时|am|<|al|
与前提矛盾,
如有两项al与al+1 同时取得绝对值最小值,那么必有am=,
此时|am|=|al|,与前提条件矛盾,
所以数列必然恒正或恒负,
在数列恒正的情况下,由②知,存在k,l且k>l,
因为是递增数列,ak>al>0,使得=a3>ak,
即3>k>l,所以=a3,此时a1,a2,a3成等比数列,
数学归纳法:
(1)已证n=3时,满足{an}是等比数列,公比q=,
(2)假设n=k时,也满足{ak}是等比数列,公比q=,
那么由①知=qak等于数列的某一项am,证明这一项为ak+1即可,
反证法:
假设这一项不是ak+1,因为是递增数列,所以该项am==qak>ak+1,
那么ak<ak+1<qak,由等比数列{ak}得a1qk﹣1<ak+1<a1qk,
由性质②得a1qk﹣1<<a1qk,同时ak+1=>am>al,s所以k+1>m>l,
所以am,al分别是等比数列{ak}中两项,即am=a1qm﹣1,al=a1ql﹣1,
原式变为a1qk﹣1<a1q2m﹣l﹣1<a1qk,
所以k﹣1<2m﹣l﹣1<k,又因为k∈N*,m∈N*,l∈N*,不存在这组解,所以矛盾,
所以知=qak=ak+1,{ak+1}为等比数列,
由数学归纳法知,{an}是等比数列得证,
同理,数列恒负,{an}也是等比数列.
四.数列的应用(共2小题)
5.(2022 北京)已知Q:a1,a2,…,ak为有穷整数数列.给定正整数m,若对任意的n∈{1,2,…,m},在Q中存在ai,ai+1,ai+2,…,ai+j(j≥0),使得ai+ai+1+ai+2+…+ai+j=n,则称Q为m﹣连续可表数列.
(Ⅰ)判断Q:2,1,4是否为5﹣连续可表数列?是否为6﹣连续可表数列?说明理由;
(Ⅱ)若Q:a1,a2,…,ak为8﹣连续可表数列,求证:k的最小值为4;
(Ⅲ)若Q:a1,a2,…,ak为20﹣连续可表数列,且a1+a2+…+ak<20,求证:k≥7.
【解析】解:(Ⅰ)若m=5,则对于任意的n∈{1,2,3,4,5},
a2=1,a1=2,a1+a2=2+1=3,a3=4,a2+a3=1+4=5,
所以Q是5﹣连续可表数列;
由于不存在任意连续若干项之和相加为6,
所以Q不是6﹣连续可表数列;
(Ⅱ)假设k的值为3,则a1,a2,a3 最多能表示a1,a2,a3,a1+a2,a2+a3,a1+a2+a3,共6个数字,
与Q是8﹣连续可表数列矛盾,故k≥4;
现构造Q:1,2,3,4可以表达出1,2,3,4,5,6,7,8这8个数字,即存在k=4满足题意.
故k的最小值为4.
(Ⅲ)先证明k≥6.
从5个正整数中,取一个数字只能表示自身,最多可表示5个数字,
取连续两个数字最多能表示4个数字,取连续三个数字最多能表示3个数字,
取连续四个数字最多能表示2个数字,取连续五个数字最多能表示1个数字,
所以对任意给定的5个整数,最多可以表示5+4+3+2+1=15个正整数,不能表示20个正整数,即k≥6.
若k=6,最多可以表示6+5+4+3+2+1=21个正整数,
由于Q为20﹣连续可表数列,且a1+a2+…+ak<20,
所以其中必有一项为负数.
既然5个正整数都不能连续可表1﹣20的正整数,
所以至少要有6个正整数连续可表1﹣20的正整数,
所以至少6个正整数和一个负数才能满足题意,
这是不可能成立的,故k≠6.
故k≥7.
6.(2021 北京)设p为实数.若无穷数列{an}满足如下三个性质,则称{an} 为 p数列:
①a1+p≥0,且a2+p=0;
②a4n﹣1<a4n(n=1,2,…);
③am+n∈{am+an+p,am+an+p+1}(m=1,2,…;n=1,2,…).
(Ⅰ)如果数列{an}的前四项为2,﹣2,﹣2,﹣1,那么{an}是否可能为 2数列?说明理由;
(Ⅱ)若数列{an}是 0数列,求a5;
(Ⅲ)设数列{an}的前n项和为Sn,是否存在 p数列{an},使得Sn≥S10恒成立?如果存在,求出所有的p;如果不存在,说明理由.
【解析】解:(Ⅰ)数列{an}不可能为 2数列,理由如下,
因为p=2,a1=2,a2=﹣2,所以a1+a2+p=2,a1+a2+p+1=3,
因为a3=﹣2,所以a3 {a1+a2+p,a1+a2+p+1},
所以数列{an}不满足性质③.
(Ⅱ)性质①,a1≥0,a2=0;
由性质③am+2∈{am,am+1},因此a3=a1或a3=a1+1,a4=0或a4=1,
若a4=0,由性质②可得a3<a4,即a1<0或a1+1<0,矛盾;
若a4=1,a3=a1+1,由a3<a4,则a1+1<1,矛盾,
因此只能是a4=1,a3=a1,
又因为a4=a1+a3或a4=a1+a3+1,所以a1=或a1=0.
若a1=,则a2∈{a1+a1+0,a1+a1+0+1}={2a1,2a1+1}={1,2},不满足a2=0,舍去;
当a1=0,则{an}的前四项为0,0,0,1,
下面用数学归纳法证明a4n+i=n(i=1,2,3),a4n+4=n+1(n∈N),
当n=0时,经检验命题成立;
假设n≤k(k≥0)时命题成立.
当n=k+1时,
若i=1,则a4(k+1)+1=a4k+5=aj+(4k+5﹣j),
利用性质③:{aj+a4k+5﹣j|j∈N*,1≤j≤4k+4}={k,k+1},此时可得a4k+5=k+1,
否则a4k+5=k,取k=0可得a5=0,而由性质②可得a5=a1+a4∈{1,2},与a5=0矛盾.
同理可得,{aj+a4k+6﹣j|j∈N*,1≤j≤4k+5}={k,k+1},此时可得a4k+6=k+1,
{aj+a4k+8﹣j|j∈N*,2≤j≤4k+6}={k+1,k+2},此时可得a4k+8=k+2,
{aj+a4k+7﹣j|j∈N*,1≤j≤4k+6}={k+1},又因为a4k+7<a4k+8,此时可得a4k+7=k+1,
即当n=k+1时,命题成立.
综上可得,a5=a4×1+1=1;
(Ⅲ)令bn=an+p,由性质③可知, m,n∈N*,bm+n=am+n+p∈{am+p+an+p,am+p+an+p+1}={bm+bn,bm+bn+1},
由于b1=a1+p≥0,b2=a2+p=0,b4n﹣1=a4n﹣1+p<a4n+p=b4n,
因此数列{bn}为 0数列,
由(Ⅱ)可知,若 n∈N*,a4n+i=n﹣p(i=1,2,3),a4n+1=n+1﹣p;
S11﹣S10=a11=a4×2+3=2﹣p≥0,
S9﹣S10=﹣a10=﹣a4×2+2=﹣(2﹣p)≥0,
因此p=2,此时a1,a2, ,a10≤0,aj≥0(j≥11),满足题意.
五.列举法计算基本事件数及事件发生的概率(共1小题)
7.(2020 北京)某校为举办甲、乙两项不同活动,分别设计了相应的活动方案;方案一、方案二.为了解该校学生对活动方案是否支持,对学生进行简单随机抽样,获得数据如表:
男生 女生
支持 不支持 支持 不支持
方案一 200人 400人 300人 100人
方案二 350人 250人 150人 250人
假设所有学生对活动方案是否支持相互独立.
(Ⅰ)分别估计该校男生支持方案一的概率、该校女生支持方案一的概率;
(Ⅱ)从该校全体男生中随机抽取2人,全体女生中随机抽取1人,估计这3人中恰有2人支持方案一的概率;
(Ⅲ)将该校学生支持方案二的概率估计值记为p0.假设该校一年级有500名男生和300名女生,除一年级外其他年级学生支持方案二的概率估计值记为p1.试比较p0与p1的大小.(结论不要求证明)
【解析】解:(Ⅰ)设“该校男生支持方案一”为事件A,“该校女生支持方案一”为事件B,
则;
(Ⅱ)由(Ⅰ)知,,
设“这3人中恰有2人支持方案一”为事件C,
则;
(Ⅲ)p0>p1.理由如下:
,设该校总人数为a,则该校支持方案二的人数约为,
由表可知,男生支持方案二的概率为,女生支持方案二的概率为,
所以一年级支持方案二的人数约为,
故除一年级外其他年级支持方案二的概率为.
六.离散型随机变量的期望与方差(共2小题)
8.(2022 北京)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:m):
甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;
乙:9.78,9.56,9.51,9.36,9.32,9.23;
丙:9.85,9.65,9.20,9.16.
假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.
(Ⅰ)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(Ⅱ)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望EX;
(Ⅲ)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)
【解析】解:(Ⅰ)甲以往的10次成绩中有4次获得优秀奖,用频率估计概率,则甲在校运动会铅球比赛中获得优秀奖的概率=.
(Ⅱ)用频率估计概率,则乙在校运动会铅球比赛中获得优秀奖的概率为=,丙在校运动会铅球比赛中获得优秀奖的概率为=,
X的所有可能取值为0,1,2,3,
则P(X=0)==,
P(X=1)===,
P(X=2)==,
P(X=3)===,
∴EX=0×=.
(Ⅲ)丙获得冠军的概率估计值最大.
9.(2021 北京)在核酸检测中,“k合1”混采核酸检测是指:先将k个人的样本混合在一起进行1次检测,如果这k个人都没有感染新冠病毒,则检测结果为阴性,得到每人的检测结果都为阴性,检测结束;如果这k个人中有人感染新冠病毒,则检测结果为阳性,此时需对每人再进行1次检测,得到每人的检测结果,检测结束.
现对100人进行核酸检测,假设其中只有2人感染新冠病毒,并假设每次检测结果准确.
(Ⅰ)将这100人随机分成10组,每组10人,且对每组都采用“10合1”混采核酸检测.
(ⅰ)如果感染新冠病毒的2人在同一组,求检测的总次数:
(ⅱ)已知感染新冠病毒的2人分在同一组的概率为.设X是检测的总次数,求X的分布列与数学期望E(X).
(Ⅱ)将这100人随机分成20组,每组5人,且对每组都采用“5合1”混采核酸检测.设Y是检测的总次数,试判断数学期望E(Y)与(Ⅰ)中E(X)的大小.(结论不要求证明)
【解析】解:(Ⅰ)(ⅰ)若采用“10合1检测法”,每组检查一次,共10次;
又两名患者在同一组,需要再检查10次,
因此一共需要检查20次.
(ⅱ)由题意可得:X=20,30.
P(X=20)=,P(X=30)=.
可得分布列:
X 20 30
P
E(X)=20×+30×=.
(Ⅱ)由题意可得:Y=25,30.
P(Y=25)=20×=,P(Y=30)=.
可得分布列:
Y 25 30
P
E(Y)=25×+30×=>=.
E(X)<E(Y).
另解:设“10合1”混采核酸检测两名感染患者在同一组的概率为p1,“5合1”混采核酸检测两名感染患者在同一组的概率为p2,则p1>p2,
此时有E(X)=20p1+30(1﹣p1)=30﹣10p1;
而E(Y)=25p2+30(1﹣p2)=30﹣5p2>30﹣5p1>30﹣10p1=E(X),
∴E(X)<E(Y).
七.正弦定理(共2小题)
10.(2021 北京)在△ABC中,c=2bcosB,∠C=.
(Ⅰ)求∠B;
(Ⅱ)再在条件①、条件②、条件③这三个条件中选择一个作为已知,使△ABC存在且唯一确定,并求BC边上的中线的长.
条件①c=b;
条件②△ABC的周长为4+2;
条件③△ABC的面积为.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
【解析】解:(Ⅰ)∵c=2bcosB,
由正弦定理可得sinC=2sinBcosB,即sinC=sin2B,
∵C=,
∴当C=2B 时,B=,即C+B=π,不符合题意,舍去,
∴C+2B=π,
∴2B=,
即B=.
(Ⅱ)选①c=b,
由正弦定理可得
,与已知条件c=b矛盾,故△ABC不存在,
选②周长为4+2,
∵C=,B=,
∴,
由正弦定理可得,即,
∴,
∴a+b+c=(2+)R=4+2,
∴R=2,即a=2,b=2,c=2,
∴△ABC存在且唯一确定,
设BC的中点为D,
∴CD=1,
在△ACD中,运用余弦定理,AD2=AC2+CD2﹣2AC CD cos∠C,
即,AD=,
∴BC边上的中线的长度.
选③面积为S△ABC=,
∵,
∴a=b,
∴,解得a=,
余弦定理可得
AD2=AC2+CD2﹣2×AC×CD×=,
.
11.(2020 北京)在△ABC中,a+b=11,再从条件①、条件②这两个条件中选择一个作为已知,求:
(Ⅰ)a的值;
(Ⅱ)sinC和△ABC的面积.
条件①:c=7,cosA=﹣;
条件②:cosA=,cosB=.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解析】解:选择条件①(Ⅰ)由余弦定理得a2=b2+c2﹣2bccosA,即a2﹣b2=49﹣14b×(﹣)=49+2b,
∴(a+b)(a﹣b)=49+2b,
∵a+b=11,
∴11a﹣11b=49+2b,
即11a﹣13b=49,
联立,解得a=8,b=3,
故a=8.
(Ⅱ)在△ABC中,sinA>0,
∴sinA==,
由正弦定理可得=,
∴sinC===,
∴S△ABC=absinC=×8×3×=6.
选择条件②(Ⅰ)在△ABC中,sinA>0,sinB>0,C=π﹣(A+B),
∵cosA=,cosB=,
∴sinA==,sinB==,
由正弦定理可得=,
∴==,
∵a+b=11,
∴a=6,b=5,
故a=6;
(Ⅱ)在△ABC中,C=π﹣(A+B),
∴sinC=sin(A+B)=sinAcosB+cosAsinB=×+×=,
∴S△ABC=absinC=×6×5×=
八.解三角形(共1小题)
12.(2022 北京)在△ABC中,sin2C=sinC.
(Ⅰ)求∠C;
(Ⅱ)若b=6,且△ABC的面积为6,求△ABC的周长.
【解析】解:(Ⅰ)∵sin2C=sinC,
∴2sinCcosC=sinC,
又sinC≠0,∴2cosC=,
∴cosC=,∵0<C<π,
∴C=;
(Ⅱ)∵△ABC的面积为6,
∴absinC=6,
又b=6,C=,
∴×a×6×=6,
∴a=4,
又cosC=,
∴=,
∴c=2,
∴a+b+c=6+6,
∴△ABC的周长为6+6.
九.直线与椭圆的综合(共3小题)
13.(2022 北京)已知椭圆E:+=1(a>b>0)的一个顶点为A(0,1),焦距为2.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(﹣2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N.当|MN|=2时,求k的值.
【解析】解:(Ⅰ)由题意得,
,∴b=1,c=,a=2,
∴椭圆E的方程为+y2=1.
(Ⅱ)设过点P(﹣2,1)的直线为y﹣1=k(x+2),B(x1,y1),C(x2,y2),
联立得,即(1+4k2)x2+(16k2+8k)x+16k2+16k=0,
∵直线与椭圆相交,∴Δ=[(16k2+8k)]2﹣4(1+4k2)(16k2+16k)>0,∴k<0,
由韦达定理得x1+x2=﹣,x1 x2=,
∵kAB=,∴直线AB为y=x+1,
令y=0,则x=,∴M(,0),同理N(,0),
∴|MN|=|﹣|=|﹣|=|(﹣)|
=| |=| |
=||=2,
∴| |=2,∴||=,
∴k=﹣4.
14.(2021 北京)已知椭圆E:+=1(a>b>0)的一个顶点A(0,﹣2),以椭圆E的四个顶点围成的四边形面积为4.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点P(0,﹣3)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB、AC分别与直线y=﹣3交于点M、N,当|PM|+|PN|≤15时,求k的取值范围.
【解析】解:(Ⅰ)因为椭圆E:+=1(a>b>0)过点A(0,﹣2),则b=2,
又因为以四个顶点围成的四边形面积为4,
所以,解得a=,
故椭圆E的标准方程为;
(Ⅱ)由题意,设过点P(0,﹣3),斜率为k的直线为直线l,
设直线l的方程为y﹣(﹣3)=k(x﹣0),即y=kx﹣3,
当k=0时,直线l与椭圆E没有交点,而直线l交椭圆E于不同的两点B,C,
所以k≠0,
设B(x1,y1),C(x2,y2),
联立方程组,可得(4+5k2)x2﹣30kx+25=0,
则Δ=(﹣30k)2﹣4×25(4+5k2)>0,解得|k|>1,
所以,
则y1y2=(kx1﹣3)(kx2﹣3)=k2x1x2﹣3k(x1+x2)+9=,
y1+y2=(kx1﹣3)+(kx2﹣3)=k(x1+x2)﹣6=,
直线AB的方程为y﹣(﹣2)=,即,
直线AC的方程为y﹣(﹣2)=,即,
因为直线AB交y=﹣3于点M,
所以令y=﹣3,则,
故,
同理可得,
注意到>0,所以x1,x2同号,
因为y1+2>0,y2+2>0,所以xM,xN同号,
故|PM|+|PN|=|xM|+|xN|=|xM+xN|,
则|PM|+|PN|==
=
=
=
=5|k|,
故|PM|+|PN|=5|k|,
又|PM|+|PN|≤15,即5|k|≤15,即|k|≤3,又|k|>1,
所以1<|k|≤3,
故k的取值范围为[﹣3,﹣1)∪(1,3].
15.(2020 北京)已知椭圆C:+=1过点A(﹣2,﹣1),且a=2b.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(﹣4,0)的直线l交椭圆C于点M,N,直线MA,NA分别交直线x=﹣4于点P,Q.求的值.
【解析】解:(Ⅰ)椭圆C:+=1过点A(﹣2,﹣1),且a=2b,
则,解得b2=2,a2=8,
∴椭圆方程为+=1,
(Ⅱ)由题意可得直线l的斜率存在,设直线方程为y=k(x+4),
由,
消y整理可得(1+4k2)x2+32k2x+64k2﹣8=0,
∴Δ=﹣32(4k2﹣1)>0,
解得﹣<k<,
设M(x1,y1),N(x2,y2),
∴x1+x2=﹣,x1x2=,
则直线AM的方程为y+1=(x+2),直线AN的方程为y+1=(x+2),
分别令x=﹣4,
可得yP=﹣1=﹣,yQ=﹣
∴|PB|=|yP|=||,|QB|=|yQ|=||,
∴=||=||
∵(2k+1)x1x2+(4k+2)(x1+x2)+8(2k+1)=,
∴||=||=||=1,
故=1.
一十.直线与平面所成的角(共2小题)
16.(2022 北京)如图,在三棱柱ABC﹣A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.
(Ⅰ)求证:MN∥平面BCC1B1;
(Ⅱ)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.
条件①:AB⊥MN;
条件②:BM=MN.
注:如果选择条件①和条件②分别解答,按第一个解答计分.
【解析】解:(I)证明:取AB中点K,连接NK,MK,
∵M,为A1B1的中点.∴B1M∥BK,且B1M∥BK,
∴四边形BKMB1是平行四边形,故MK∥BB1,
MK 平面BCC1B1;BB1 平面BCC1B1,
∴MK∥平面BCC1B1,
∵K是AB中点,N是AC的点,
∴NK∥BC,∵NK 平面BCC1B1;BC 平面BCC1B1,
∴NK∥平面BCC1B1,又NK∩MK=K,
∴平面NMK∥平面BCC1B1,
又MN 平面NMK,∴MN∥平面BCC1B1;
(II)∵侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,平面BCC1B1∩平面ABB1A1=BB1,
∴CB⊥平面ABB1A1,∴CB⊥AB,又NK∥BC,∴AB⊥NK,
若选①:AB⊥MN;又MN∩NK=N,∴AB⊥平面MNK,
又MK 平面MNK,∴AB⊥MK,又MK∥BB1,
∴AB⊥BB1,∴BC,BA,BB1两两垂直,
若选②:∵CB⊥平面ABB1A1,NK∥BC,∴NK⊥平面ABB1A1,KM 平面ABB1A1,
∴MK⊥NK,又BM=MN,NK=BC,BK=AB,
∴△BKM≌△NKM,∴∠BKM=∠NKM=90°,
∴AB⊥MK,又MK∥BB1,∴AB⊥BB1,
∴BC,BA,BB1两两垂直,
以B为坐标原点,BC,BA,BB1为坐标轴建立如图所示的空间直角坐标系,
则B(0,0,0),N(1,1,0),M(0,1,2),A(0,2,0),
∴=(0,1,2),=(1,1,0),
设平面BMN的一个法向量为=(x,y,z),
则,令z=1,则y=﹣2,x=2,
∴平面BMN的一个法向量为=(2,﹣2,1),
又=(0,2,0),
设直线AB与平面BMN所成角为θ,
∴sinθ=|cos<,>|===.
∴直线AB与平面BMN所成角的正弦值为.
17.(2020 北京)如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点.
(Ⅰ)求证:BC1∥平面AD1E;
(Ⅱ)求直线AA1与平面AD1E所成角的正弦值.
【解析】解:(Ⅰ)由正方体的性质可知,AB∥C1D1中,且AB=C1D1,
∴四边形ABC1D1是平行四边形,∴BC1∥AD1,
又BC1 平面AD1E,AD1 平面AD1E,∴BC1∥平面AD1E.
(Ⅱ)解法一:以A为原点,AD、AB、AA1分别为x、y和z轴建立如图所示的空间直角坐标系,
设正方体的棱长为a,则A(0,0,0),A1(0,0,a),D1(a,0,a),E(0,a,a),
∴,,,
设平面AD1E的法向量为,则,即,
令z=2,则x=﹣2,y=﹣1,∴=(﹣2,﹣1,2),
设直线AA1与平面AD1E所成角为θ,则sinθ=|cos<,>|==,
故直线AA1与平面AD1E所成角的正弦值为.
解法二:设正方体的棱长为2a,则AD1=a,AE=a,ED1=3a,= 2a 2a=2a2,
由余弦定理知,cos∠EAD1===,
∴sin∠EAD1=,
∴=AD1 AE sin∠EAD1=3a2,
设点A1到平面EAD1的距离为h,
∵=,
∴,∴h=,
设直线AA1与平面AD1E所成角为θ,则sinθ==.
故直线AA1与平面AD1E所成角的正弦值为.
一十一.二面角的平面角及求法(共1小题)
18.(2021 北京)如图,在正方体ABCD﹣A1B1C1D1,E为A1D1的中点,B1C1交平面CDE交于点F.
(Ⅰ)求证:F为B1C1的中点;
(Ⅱ)若点M是棱A1B1上一点,且二面角M﹣FC﹣E的余弦值为,求的值.
【解析】(Ⅰ)证明:连结DE,
在正方体ABCD﹣A1B1C1D1中,CD∥C1D1,C1D1 平面A1B1C1D1,CD 平面A1B1C1D1,
则CD∥平面A1B1C1D1,因为平面A1B1C1D1∩平面CDEF=EF,
所以CD∥EF,则EF∥C1D1,
故A1B1∥EF∥C1D1,又因为A1D1∥B1C1,
所以四边形A1B1FE为平行四边形,四边形EFC1D1为平行四边形,
所以A1E=B1F,ED1=FC1,
而点E为A1D1的中点,所以A1E=ED1,
故B1F=FC1,则点F为B1C1的中点;
(Ⅱ)解:以点B1为原点,建立空间直角坐标系,如图所示,
设正方体棱长为2,设点M(m,0,0),
因为二面角M﹣FC﹣E的余弦值为,则m<0,所以m≠0,
则C(0,2,﹣2),E(﹣2,1,0),F(0,1,0),
故,
设平面CMF的法向量为,
则,即,
所以,b=2,故,
设平面CDEF的法向量为,
则,即,
所以x=0,y=2,故,
因为二面角M﹣FC﹣E的余弦值为,
则==,
解得m=±1,又m<0,
所以m=﹣1,
故=.
同课章节目录
