沪科版七年级上册3.4.1 列二元一次方程组解实际问题课件(共24张PPT)
文档属性
| 名称 | 沪科版七年级上册3.4.1 列二元一次方程组解实际问题课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 867.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:53:21 | ||
图片预览








文档简介
(共24张PPT)
第3章 一元一次方程与方程组
3.4 二元一次方程组的应用
第1课时 列二元一次方程组解实际问题
沪科版 数学 七年级上册
1. 列二元一次方程组解应用题的基本步骤;
2. 建立二元一次方程组的模型对实际问题进行判断或方案设计.
学习目标
新知一 列二元一次方程组解应用题的基本步骤
1. 基本思想方法
(1)列方程组解应用题是把“未知”转化成“已知”的过
程,关键是把未知量与已知量联系起来,找出题目中的等量关系列方程组.
(2)一般情况下,有几个未知量就必须列出几个方程,所
列方程必须满足:①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
探究新知
2. 列二元一次方程组解应用题的一般步骤
审→设→找→列→解→答
(1)审:通过审题,把实际问题抽象成数学问题;
(2)设:分析已知量和未知量,并用字母表示其中的两个
未知量(设元);
(3)找:找出题中的两个等量关系;
(4)列:根据等量关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)答:检验所求解是否符合实际意义,写出答案.
特别解读
1.一般设几个未知数就列几个方程;
2.设未知数和写答案时,都要写清单位名称.
某船的载质量为300 吨,容积为1 200 立方米,现有甲、乙两种货物要运,其中甲种货物每吨体积为6 立方米,乙种货物每吨体积为2 立方米,要充分利用这艘船的载质量和容积,甲、乙两种货物应各装多少吨?
例1
解题秘方:分析题目中的已知量和未知量,找准题目中的等量关系,列出方程组解决问题.已知量:(1)甲种货物每吨体积为6 立方米;(2)乙种货物每吨体积为2 立方米;(3)船的载质量为300 吨;(4)船的容积为1 200 立方米.未知量:甲、乙两种货物应装的质量. 若用x,y 分别表示它们的吨数,则甲种货物的体积为6x 立方米,乙种货物的体积为2y 立方米.
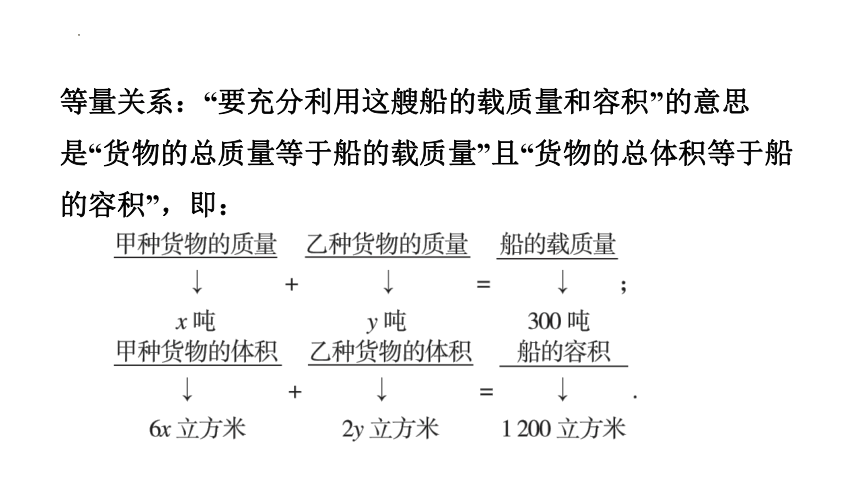
等量关系:“要充分利用这艘船的载质量和容积”的意思
是“货物的总质量等于船的载质量”且“货物的总体积等于船的容积”,即:
解法提醒
列方程组解应用题的关键是准确地找出题中的等量关系,正确地列出方程组.
找等量关系的方法:
(1) 抓住题目中的关键词,常见的关键词有:“比”“是”“等于”等;
(2) 根据常见的数量关系,如体积关系、面积关系等,找等量关系;
(3) 挖掘题目中的隐含条件,如飞机沿同一航线航行,顺风航行与逆风航行的路程相等;
(4) 借助列表格、画线段示意图等方法找等量关系.
解:设甲种货物应装x 吨,乙种货物应装y 吨.
由题意,得 解得
答:甲、乙两种货物应各装150 吨.
新知二 建立二元一次方程组的模型对实际问题进行判断或方案设计
建立二元一次方程组的模型就是为了解决实际问题. 对某个问题要进行判断或设计方案时,关键之处在于
(1)要分析解决此问题时需要解决哪几个未知量,然后
根据需要设未知数;
(2)方程组的解是否符合实际问题的限制条件.
特别提醒
设计方案问题应从不同角度去考虑,先考虑多种可能的方案,最后根据结果合理地选择方案.
某超市举行店庆活动,对甲、乙两种商品实行打折销售. 打折前,购买3 件甲商品和1 件乙商品需要190 元;购买2 件甲商品和3 件乙商品需要220 元. 而店庆期间,购买10 件甲商品和10 件乙商品仅需735 元,这比打折前少花多少钱?
解题秘方:分析解决问题的关键点是求甲、乙两商品的单
价,采取间接设未知数的方法解决问题.
例2
方法点拨
对某个实际问题进行判断时,先分析解决问题的关键点,即需要设出的未知数是哪两个,然后根据题目中给出的等量关系列出二元一次方程组.
解:设甲商品的单价为x 元,乙商品的单价为y 元.
由题意,得
解得
购买10 件甲商品和10 件乙商品需要10×(50+40)=900(元).
因为打折后实际花费735 元,
所以这比打折前少花900-735=165(元).
某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000 元;经粗加工后销售,每吨利润可达4 500 元;经精加工后销售,每吨利润涨至7 500 元. 当地一家公司收获这种蔬菜140 吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16 吨;如果进行精加工,每天可加工6 吨,但两种加工方式不能同时进行. 受季节条件的限制,公司必须在15 天之内将这批蔬菜全部销售或加工完毕,为此公司制定了三种加工方案:
例3
解题秘方:分别求出三种方案的利润,进行比较选择,求
利润时,找出与利润相关的未知量去设未知数.
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多地对蔬菜进行精加工,并将没有来得
及加工的蔬菜在市场上全部销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,
并恰好在15 天内完成.
你认为哪种方案获利最多?为什么?
解法提醒
解决优化方案问题,首先要列举出所有可能的方案,再按题中的要求分别求出每种方案的具体结果,从中选择最优方案.
解:(方案一)只对蔬菜进行粗加工,易知15 天内能全
部加工完,获利为4 500×140=630 000(元).
(方案二)尽可能多地对蔬菜进行精加工,
即精加工的质量为6×15=90(吨),
获利为7 500×90+1 000×(140-90)=725 000(元).
(方案三)设将x 吨蔬菜进行精加工,y 吨蔬菜进行粗加工.
由题意,得
解得
所以获利为7 500×60+4 500×80=810 000(元).
因为630 000 < 725 000 < 810 000,所以方案三获利最多.
二元一次方程组
列二元一次方程组解实际问题
实际问题
建模设列
检验(答)
解二元一次方程组
二元一次方程组
实际问题
建模设列
检验(答)
解二元一次方程组
列二元一次方程组解实际问题
再 见
第3章 一元一次方程与方程组
3.4 二元一次方程组的应用
第1课时 列二元一次方程组解实际问题
沪科版 数学 七年级上册
1. 列二元一次方程组解应用题的基本步骤;
2. 建立二元一次方程组的模型对实际问题进行判断或方案设计.
学习目标
新知一 列二元一次方程组解应用题的基本步骤
1. 基本思想方法
(1)列方程组解应用题是把“未知”转化成“已知”的过
程,关键是把未知量与已知量联系起来,找出题目中的等量关系列方程组.
(2)一般情况下,有几个未知量就必须列出几个方程,所
列方程必须满足:①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
探究新知
2. 列二元一次方程组解应用题的一般步骤
审→设→找→列→解→答
(1)审:通过审题,把实际问题抽象成数学问题;
(2)设:分析已知量和未知量,并用字母表示其中的两个
未知量(设元);
(3)找:找出题中的两个等量关系;
(4)列:根据等量关系列出方程组;
(5)解:解这个方程组,求出未知数的值;
(6)答:检验所求解是否符合实际意义,写出答案.
特别解读
1.一般设几个未知数就列几个方程;
2.设未知数和写答案时,都要写清单位名称.
某船的载质量为300 吨,容积为1 200 立方米,现有甲、乙两种货物要运,其中甲种货物每吨体积为6 立方米,乙种货物每吨体积为2 立方米,要充分利用这艘船的载质量和容积,甲、乙两种货物应各装多少吨?
例1
解题秘方:分析题目中的已知量和未知量,找准题目中的等量关系,列出方程组解决问题.已知量:(1)甲种货物每吨体积为6 立方米;(2)乙种货物每吨体积为2 立方米;(3)船的载质量为300 吨;(4)船的容积为1 200 立方米.未知量:甲、乙两种货物应装的质量. 若用x,y 分别表示它们的吨数,则甲种货物的体积为6x 立方米,乙种货物的体积为2y 立方米.
等量关系:“要充分利用这艘船的载质量和容积”的意思
是“货物的总质量等于船的载质量”且“货物的总体积等于船的容积”,即:
解法提醒
列方程组解应用题的关键是准确地找出题中的等量关系,正确地列出方程组.
找等量关系的方法:
(1) 抓住题目中的关键词,常见的关键词有:“比”“是”“等于”等;
(2) 根据常见的数量关系,如体积关系、面积关系等,找等量关系;
(3) 挖掘题目中的隐含条件,如飞机沿同一航线航行,顺风航行与逆风航行的路程相等;
(4) 借助列表格、画线段示意图等方法找等量关系.
解:设甲种货物应装x 吨,乙种货物应装y 吨.
由题意,得 解得
答:甲、乙两种货物应各装150 吨.
新知二 建立二元一次方程组的模型对实际问题进行判断或方案设计
建立二元一次方程组的模型就是为了解决实际问题. 对某个问题要进行判断或设计方案时,关键之处在于
(1)要分析解决此问题时需要解决哪几个未知量,然后
根据需要设未知数;
(2)方程组的解是否符合实际问题的限制条件.
特别提醒
设计方案问题应从不同角度去考虑,先考虑多种可能的方案,最后根据结果合理地选择方案.
某超市举行店庆活动,对甲、乙两种商品实行打折销售. 打折前,购买3 件甲商品和1 件乙商品需要190 元;购买2 件甲商品和3 件乙商品需要220 元. 而店庆期间,购买10 件甲商品和10 件乙商品仅需735 元,这比打折前少花多少钱?
解题秘方:分析解决问题的关键点是求甲、乙两商品的单
价,采取间接设未知数的方法解决问题.
例2
方法点拨
对某个实际问题进行判断时,先分析解决问题的关键点,即需要设出的未知数是哪两个,然后根据题目中给出的等量关系列出二元一次方程组.
解:设甲商品的单价为x 元,乙商品的单价为y 元.
由题意,得
解得
购买10 件甲商品和10 件乙商品需要10×(50+40)=900(元).
因为打折后实际花费735 元,
所以这比打折前少花900-735=165(元).
某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000 元;经粗加工后销售,每吨利润可达4 500 元;经精加工后销售,每吨利润涨至7 500 元. 当地一家公司收获这种蔬菜140 吨,该公司的加工生产能力是:如果对蔬菜进行粗加工,每天可加工16 吨;如果进行精加工,每天可加工6 吨,但两种加工方式不能同时进行. 受季节条件的限制,公司必须在15 天之内将这批蔬菜全部销售或加工完毕,为此公司制定了三种加工方案:
例3
解题秘方:分别求出三种方案的利润,进行比较选择,求
利润时,找出与利润相关的未知量去设未知数.
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多地对蔬菜进行精加工,并将没有来得
及加工的蔬菜在市场上全部销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,
并恰好在15 天内完成.
你认为哪种方案获利最多?为什么?
解法提醒
解决优化方案问题,首先要列举出所有可能的方案,再按题中的要求分别求出每种方案的具体结果,从中选择最优方案.
解:(方案一)只对蔬菜进行粗加工,易知15 天内能全
部加工完,获利为4 500×140=630 000(元).
(方案二)尽可能多地对蔬菜进行精加工,
即精加工的质量为6×15=90(吨),
获利为7 500×90+1 000×(140-90)=725 000(元).
(方案三)设将x 吨蔬菜进行精加工,y 吨蔬菜进行粗加工.
由题意,得
解得
所以获利为7 500×60+4 500×80=810 000(元).
因为630 000 < 725 000 < 810 000,所以方案三获利最多.
二元一次方程组
列二元一次方程组解实际问题
实际问题
建模设列
检验(答)
解二元一次方程组
二元一次方程组
实际问题
建模设列
检验(答)
解二元一次方程组
列二元一次方程组解实际问题
再 见
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
