人教B版(2019)数学必修第四册 9.1.1正弦定理 课件(共49张PPT)
文档属性
| 名称 | 人教B版(2019)数学必修第四册 9.1.1正弦定理 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-22 22:48:00 | ||
图片预览








文档简介
(共49张PPT)
9.1.1 正弦定理
一、三角形的面积
1.思考
三角形的面积公式是如何证明的
(1)三角形的高的计算公式:
在△ABC中,边BC,CA,AB对应的边长分别为a,b,c,边上的高分别记为ha,hb,hc,则ha=bsin C=csin B,hb=csin A=asin C,hc=asin B=bsin A.
借助上述结论,如图,若已知△ABC中的边AC,AB,角A,那么AB边上的高CD=bsin A,△ABC的面积
提示:
(2)三角形的面积与内切圆:
答案:60°或120°
(2)在△ABC中,A=30°,AB=2,BC=1,则△ABC的面积等于 .
二、正弦定理
1.思考
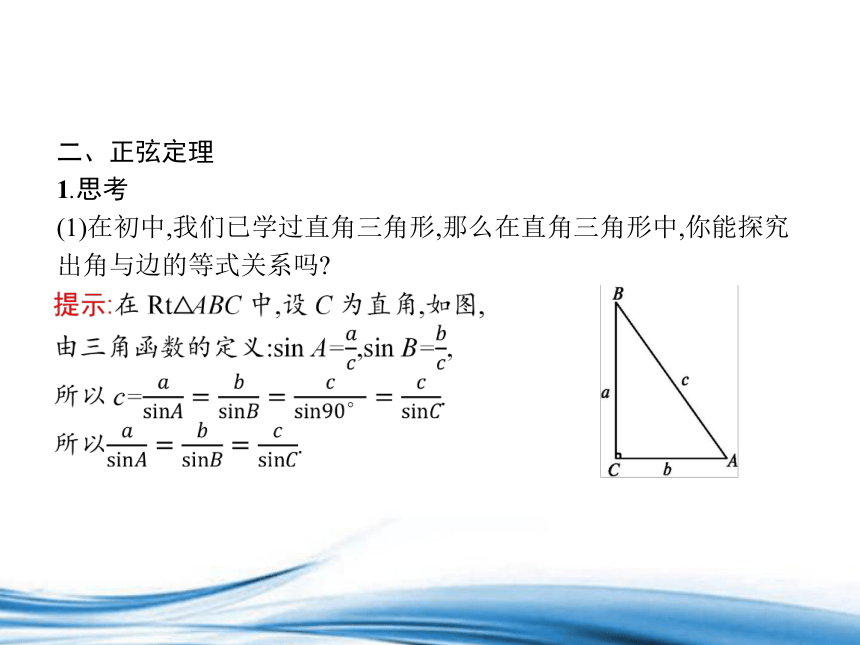
(1)在初中,我们已学过直角三角形,那么在直角三角形中,你能探究出角与边的等式关系吗
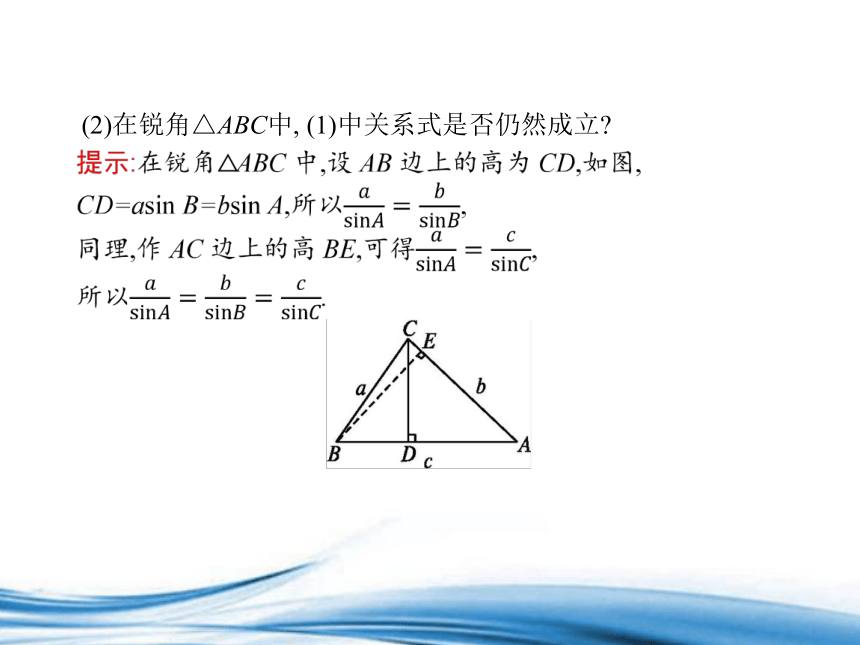
(2)在锐角△ABC中, (1)中关系式是否仍然成立
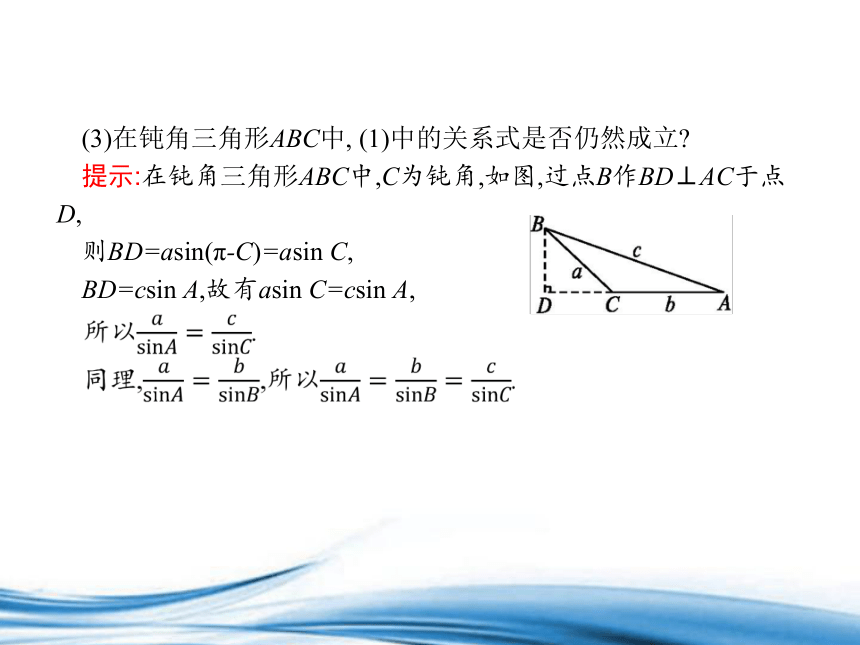
(3)在钝角三角形ABC中, (1)中的关系式是否仍然成立
提示:在钝角三角形ABC中,C为钝角,如图,过点B作BD⊥AC于点D,
则BD=asin(π-C)=asin C,
BD=csin A,故有asin C=csin A,
2.填空
(1)正弦定理的表示
3.做一做
(1)判断正误.
①正弦定理只适用于锐角三角形. ( )
②正弦定理不适用于钝角三角形. ( )
③在某一确定的三角形中,各边与它的对角的正弦的比是定值. ( )
④在△ABC中,sin A∶sin B∶sin C=a∶b∶c. ( )
解析:正弦定理适用于任意三角形,故①②均不正确;
由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比就确定了,故③正确;
由比例性质和正弦定理可推知④正确.
答案:①× ②× ③√ ④√
答案:C
(3)在△ABC中,A∶B∶C=4∶1∶1,则a∶b∶c= ( )
答案:D
三、解三角形
1.思考
从正弦定理的表达形式上,你能说明正弦定理的基本作用吗
提示:(1)正弦定理说明在同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,即存在正数k使a=ksin A,b=ksin B,c=ksin C;
从而知正弦定理的基本作用:利用正弦定理可以解决以下两类有关三角形的问题:
①已知两角和任意一边,求其他两边和第三个角;
②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.
2.填空
习惯上,我们把三角形的3个角与3条边都称为三角形的元素.已知三角形的若干元素求其他元素一般称为解三角形.
3.做一做
答案:D
答案:45°
四、对三角形解的个数的判断
1.思考
(1)在△ABC中,若A>B,一定有sin A>sin B吗 反之,若sin A>sin B,是否也一定有A>B
提示:由A>B,得a>b,
所以2Rsin A>2Rsin B,即sin A>sin B;
由sin A>sin B,得2Rsin A>2Rsin B,即a>b.
所以A>B.
(2)如何判断三角形解的个数 对于任意给定的a,b,A的值,能否确定一个三角形
提示:略
2.填空
已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.现以已知a,b和A解三角形为例,从两个方面予以说明:
(2)几何角度
3.做一做
不解三角形,判断下列三角形解的个数.
(1)a=5,b=4,A=120°;
(2)a=7,b=14,A=150°;
(3)a=9,b=10,A=60°.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
正弦定理的简单应用
例1(1)在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
解:(1)因为A=45°,C=30°,
所以B=180°-(A+C)=105°.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟正弦定理的两个应用
(1)已知两角与任意一边解三角形的方法:如果已知三角形的任意两个角与一边解三角形时,由三角形内角和定理可以计算出三角形的另一角,由正弦定理可计算出三角形的另两边.
(2)已知三角形两边和其中一边的对角解三角形的方法:
首先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中大边对大角看能否判断所求这个角是锐角,当已知的角为大边所对的角时,则能判断另一边所对的角为锐角,当已知的角为小边所对的角时,则不能判断,此时就有两组解,再分别求解即可;然后由三角形内角和定理求出第三个角;最后根据正弦定理求出第三条边.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练1(1)在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
答案:C
A.30° B.45°或135°
C.60° D.135°
答案:B
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
答案:105°或15°
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
求三角形的面积
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判定三角形的形状
例3在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin B·cos C.试判断△ABC的形状.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟判断三角形形状的方法
(1)判断三角形的形状,可以从考查三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系或求出角与角的关系或角的大小,从而作出准确判断.
(2)判断三角形的形状,主要看其是不是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练3在△ABC中,若b=acos C,试判断该三角形的形状.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判断三角形解的个数
例4已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,有解的作出解答.
(1)a=10,b=20,A=80°;
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟已知三角形两边和其中一边的对角时,判断三角形解的个数
已知三角形两边和其中一边的对角时,利用正弦定理求出另一边对角的正弦值后,需利用三角形中“大边对大角”来判断此角是锐角、直角还是钝角,从而确定三角形有两解还是只有一解.也可以用几何法来判断,即比较已知角的对边与另一边和该角正弦值乘积的大小来确定解的个数.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练4(1)满足a=4,b=3,A=45°的三角形ABC的个数为 .
解析:因为A=45°<90°,a=4>3=b,所以△ABC的个数为1.
答案:1
(2)在△ABC中,a=x,b=2,B=45°.若该三角形有两解,则x的取值范围是 .
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
用正弦定理证明问题
例5在任意△ABC中,求证:a(sin B-sin C)+b(sin C-sin A)+c(sin A-sin B)=0.
证明:由正弦定理,令a=ksin A,b=ksin B,c=ksin C,代入得:
左边=k(sin Asin B-sin Asin C+sin Bsin C-sin Bsin A+sin Csin A-sin Csin B)=0=右边,
所以等式成立.
反思感悟边与角的互化方法
正弦定理的变形公式a=ksin A,b=ksin B,c=ksin C(k>0)能够使三角形边与角的关系相互转化.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练5利用正弦定理证明定理:等腰三角形的两个底角相等.
证明:设等腰△ABC的两边AB=AC,
所以sin C=sin B.
由于0°所以B=C.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
正弦定理与三角恒等变换知识的综合应用
例6在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a=1,
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判断三角形解的个数的多种方法
典例在△ABC中,角A,B,C的对边分别为a,b,c,a=4,A=30°,b=x(x>0),判断此三角形解的个数.
解:由于b是不确定的边长,无法知道a与b的大小关系,即无法判断B是锐角还是钝角,这就需要对x的取值进行分类讨论.
所以B有两种结果,此时△ABC有两解.
当x=8时,sin B=1,则B=90°,此时△ABC有一解.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
综上可知:当08时,△ABC无解.
解法二:A=30°,是锐角,分三种情况:
①当a=bsin A或a≥b,即4=xsin 30°或4≥x,
即x=8或0②当xsin 30°<4③当48时,三角形无解.
综上可知,当0当4当x>8时,△ABC无解.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
1.在△ABC中,sin A=sin C,则△ABC一定是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
答案:B
2.在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
答案:C
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
答案:75°
4.已知△ABC的外接圆半径是2 cm,∠A=60°,则BC边的长为 .
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
9.1.1 正弦定理
一、三角形的面积
1.思考
三角形的面积公式是如何证明的
(1)三角形的高的计算公式:
在△ABC中,边BC,CA,AB对应的边长分别为a,b,c,边上的高分别记为ha,hb,hc,则ha=bsin C=csin B,hb=csin A=asin C,hc=asin B=bsin A.
借助上述结论,如图,若已知△ABC中的边AC,AB,角A,那么AB边上的高CD=bsin A,△ABC的面积
提示:
(2)三角形的面积与内切圆:
答案:60°或120°
(2)在△ABC中,A=30°,AB=2,BC=1,则△ABC的面积等于 .
二、正弦定理
1.思考
(1)在初中,我们已学过直角三角形,那么在直角三角形中,你能探究出角与边的等式关系吗
(2)在锐角△ABC中, (1)中关系式是否仍然成立
(3)在钝角三角形ABC中, (1)中的关系式是否仍然成立
提示:在钝角三角形ABC中,C为钝角,如图,过点B作BD⊥AC于点D,
则BD=asin(π-C)=asin C,
BD=csin A,故有asin C=csin A,
2.填空
(1)正弦定理的表示
3.做一做
(1)判断正误.
①正弦定理只适用于锐角三角形. ( )
②正弦定理不适用于钝角三角形. ( )
③在某一确定的三角形中,各边与它的对角的正弦的比是定值. ( )
④在△ABC中,sin A∶sin B∶sin C=a∶b∶c. ( )
解析:正弦定理适用于任意三角形,故①②均不正确;
由正弦定理可知,三角形一旦确定,则各边与其所对角的正弦的比就确定了,故③正确;
由比例性质和正弦定理可推知④正确.
答案:①× ②× ③√ ④√
答案:C
(3)在△ABC中,A∶B∶C=4∶1∶1,则a∶b∶c= ( )
答案:D
三、解三角形
1.思考
从正弦定理的表达形式上,你能说明正弦定理的基本作用吗
提示:(1)正弦定理说明在同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,即存在正数k使a=ksin A,b=ksin B,c=ksin C;
从而知正弦定理的基本作用:利用正弦定理可以解决以下两类有关三角形的问题:
①已知两角和任意一边,求其他两边和第三个角;
②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.
2.填空
习惯上,我们把三角形的3个角与3条边都称为三角形的元素.已知三角形的若干元素求其他元素一般称为解三角形.
3.做一做
答案:D
答案:45°
四、对三角形解的个数的判断
1.思考
(1)在△ABC中,若A>B,一定有sin A>sin B吗 反之,若sin A>sin B,是否也一定有A>B
提示:由A>B,得a>b,
所以2Rsin A>2Rsin B,即sin A>sin B;
由sin A>sin B,得2Rsin A>2Rsin B,即a>b.
所以A>B.
(2)如何判断三角形解的个数 对于任意给定的a,b,A的值,能否确定一个三角形
提示:略
2.填空
已知三角形的两角和任意一边,求另两边和另一角,此时有唯一解,三角形被唯一确定.已知两边和其中一边的对角,求其他的边和角,此时可能出现一解、两解或无解的情况,三角形不能被唯一确定.现以已知a,b和A解三角形为例,从两个方面予以说明:
(2)几何角度
3.做一做
不解三角形,判断下列三角形解的个数.
(1)a=5,b=4,A=120°;
(2)a=7,b=14,A=150°;
(3)a=9,b=10,A=60°.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
正弦定理的简单应用
例1(1)在△ABC中,已知c=10,A=45°,C=30°,解这个三角形.
解:(1)因为A=45°,C=30°,
所以B=180°-(A+C)=105°.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟正弦定理的两个应用
(1)已知两角与任意一边解三角形的方法:如果已知三角形的任意两个角与一边解三角形时,由三角形内角和定理可以计算出三角形的另一角,由正弦定理可计算出三角形的另两边.
(2)已知三角形两边和其中一边的对角解三角形的方法:
首先用正弦定理求出另一边所对的角的正弦值,若这个角不是直角,则利用三角形中大边对大角看能否判断所求这个角是锐角,当已知的角为大边所对的角时,则能判断另一边所对的角为锐角,当已知的角为小边所对的角时,则不能判断,此时就有两组解,再分别求解即可;然后由三角形内角和定理求出第三个角;最后根据正弦定理求出第三条边.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练1(1)在△ABC中,已知a=8,B=60°,C=75°,则b等于( )
答案:C
A.30° B.45°或135°
C.60° D.135°
答案:B
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
答案:105°或15°
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
求三角形的面积
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判定三角形的形状
例3在△ABC中,sin2A=sin2B+sin2C,且sin A=2sin B·cos C.试判断△ABC的形状.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟判断三角形形状的方法
(1)判断三角形的形状,可以从考查三边的关系入手,也可以从三个内角的关系入手,从条件出发,利用正弦定理进行代换、转化,呈现出边与边的关系或求出角与角的关系或角的大小,从而作出准确判断.
(2)判断三角形的形状,主要看其是不是正三角形、等腰三角形、直角三角形、钝角三角形或锐角三角形,要特别注意“等腰直角三角形”与“等腰三角形或直角三角形”的区别.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练3在△ABC中,若b=acos C,试判断该三角形的形状.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判断三角形解的个数
例4已知下列各三角形中的两边及其一边的对角,判断三角形是否有解,有解的作出解答.
(1)a=10,b=20,A=80°;
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
反思感悟已知三角形两边和其中一边的对角时,判断三角形解的个数
已知三角形两边和其中一边的对角时,利用正弦定理求出另一边对角的正弦值后,需利用三角形中“大边对大角”来判断此角是锐角、直角还是钝角,从而确定三角形有两解还是只有一解.也可以用几何法来判断,即比较已知角的对边与另一边和该角正弦值乘积的大小来确定解的个数.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练4(1)满足a=4,b=3,A=45°的三角形ABC的个数为 .
解析:因为A=45°<90°,a=4>3=b,所以△ABC的个数为1.
答案:1
(2)在△ABC中,a=x,b=2,B=45°.若该三角形有两解,则x的取值范围是 .
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
用正弦定理证明问题
例5在任意△ABC中,求证:a(sin B-sin C)+b(sin C-sin A)+c(sin A-sin B)=0.
证明:由正弦定理,令a=ksin A,b=ksin B,c=ksin C,代入得:
左边=k(sin Asin B-sin Asin C+sin Bsin C-sin Bsin A+sin Csin A-sin Csin B)=0=右边,
所以等式成立.
反思感悟边与角的互化方法
正弦定理的变形公式a=ksin A,b=ksin B,c=ksin C(k>0)能够使三角形边与角的关系相互转化.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
变式训练5利用正弦定理证明定理:等腰三角形的两个底角相等.
证明:设等腰△ABC的两边AB=AC,
所以sin C=sin B.
由于0°
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
正弦定理与三角恒等变换知识的综合应用
例6在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a=1,
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
判断三角形解的个数的多种方法
典例在△ABC中,角A,B,C的对边分别为a,b,c,a=4,A=30°,b=x(x>0),判断此三角形解的个数.
解:由于b是不确定的边长,无法知道a与b的大小关系,即无法判断B是锐角还是钝角,这就需要对x的取值进行分类讨论.
所以B有两种结果,此时△ABC有两解.
当x=8时,sin B=1,则B=90°,此时△ABC有一解.
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
综上可知:当0
解法二:A=30°,是锐角,分三种情况:
①当a=bsin A或a≥b,即4=xsin 30°或4≥x,
即x=8或0
综上可知,当0
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
1.在△ABC中,sin A=sin C,则△ABC一定是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
答案:B
2.在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B.3∶2∶1
答案:C
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
答案:75°
4.已知△ABC的外接圆半径是2 cm,∠A=60°,则BC边的长为 .
探究一
探究二
探究三
探究四
探究五
探究六
思维辨析
当堂检测
