10.2直方图 课件
图片预览







文档简介
课件25张PPT。10.2 直方图知识回顾我们已经学习了用哪些方法来
描述数据?统计表;条形图;折线图;
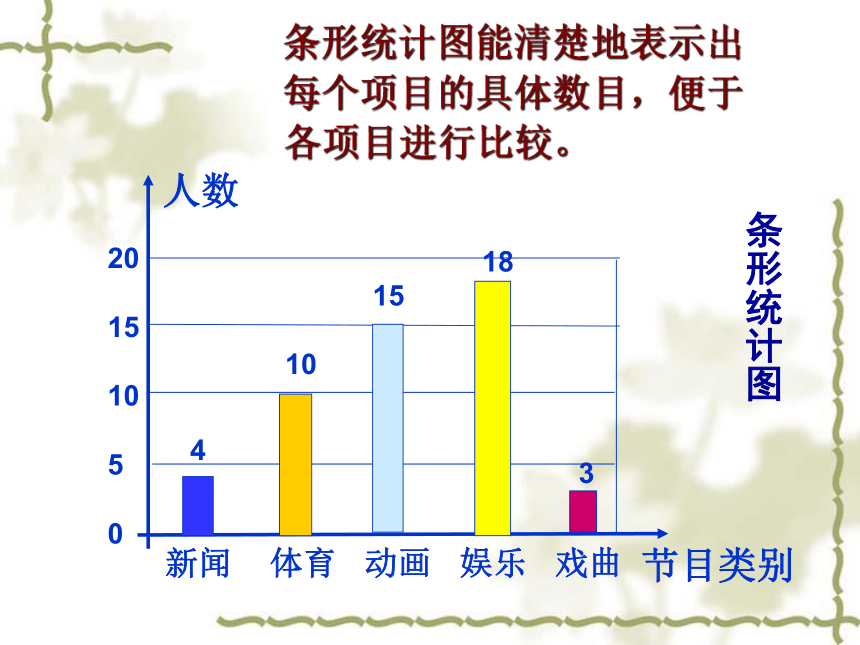
扇形图.各方法有什么特点?条形统计图能清楚地表示出
每个项目的具体数目,便于
各项目进行比较。条形统计图扇形统计图能清楚地表示出
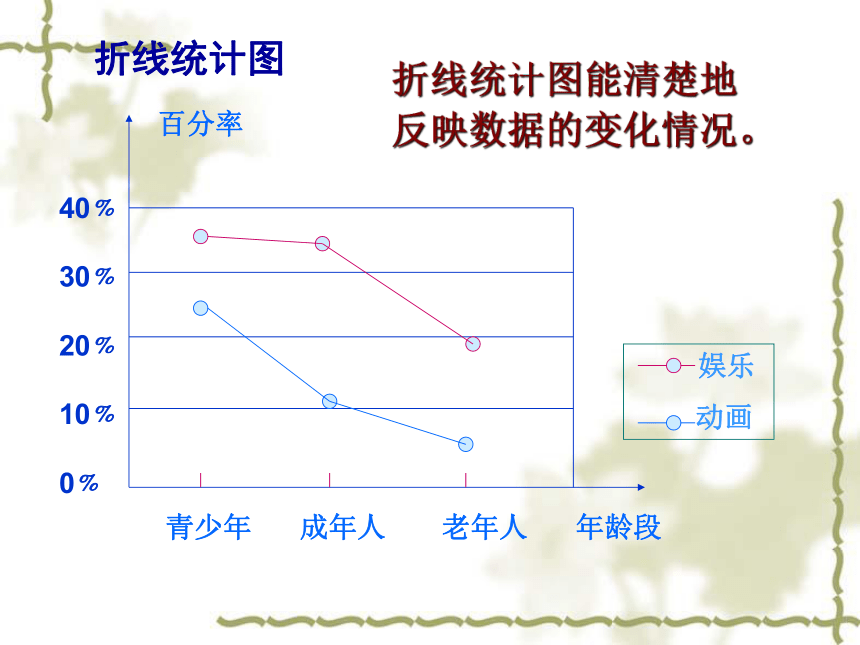
各部分在总体中所占的百分比.扇形统计图折线统计图能清楚地
反映数据的变化情况。折线统计图 为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下: 问题1问题1选择身高在哪个范围内的学生参加呢? 为了使选取的参赛选手身高比较整齐,需要知道数据的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理. 究竟分几组比较合适呢?原则上100个数以内分为5~12组较为恰当,且组数一定为正整数. 组数的多少由什么决定?总结:组数的多少由组距决定,组距越大组数越少,组距越小组数越多.对数据进行分析整理的步骤:1.计算最大值和最小值的差 在上面的数据中,最小值是149,
最大值是172,它们的差是23,说明身
高的变化范围是23 cm. 2.决定组距和组数
把所有数据分成若干组,每个小组的两
个端点之间的距离称为组距.(最大值-最小值)÷组距 所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别是8和3. 决定组数与组距的一般规律:数据越多,分得的
组数也越多。 假如数据总数为n
当n≤50时,则分为5 ~ 8组;
当50≤n≤100时,则分为8 ~ 12 组;
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表,见教材146页表10-3. 从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员. ③列频数分布表;频数:落在各个小组内的数据个数。频数分布表已经能反映数据的分布特征。 有没有更直观的表示方法呢? 画频数分布直方图的步骤:(1)以横轴表示身高,纵轴表示频数与组数的比值.(3)在等距离分组中,由于小长方形的面积就是该组的频数,所以在作频数分布直方图时,小长方形的高完全可以用频数来代替.画出频数分布直方图频数/组距身高/㎝7
6
5
4
3
2
1
0149 152 155 158 161 164 167 170 173频数分布直方图 图10.2-2 4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据表格中的数据画出频数分布直方图. 频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各个小长方形的面积(频数)与高的比是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.画频数分布直方图的一般步骤:1、 计算最大值与最小值的差(极差).
2、决定组距与组数: 极差÷组距=组数
3、列频数分布表.
数出每一组频数
4、画频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组内的频数为高,画出一个个矩形。活动 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度(单位:cm)如下表:利用新知,解决实际问题解题过程:(1)计算最大与最小值的差. 在样本数据中,最大值是7.4,最小值是4.0,它们的差是7.4-4.0=3.4(cm)。利用新知,解决实际问题(2)决定组距和组数. 对数据分组整理的步骤:利用新知,解决实际问题(3)完成频数分布表 利用新知,解决实际问题 (4)画出频数分布直方图. 通过观察频数分布直方图,你发现了什么规律吗?利用新知,解决实际问题2、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。(1)该班有 名学生;(2)70.5~80.5这一组的频数是 ,4414练习人数分数50.560.570.580.590.5100.52.根据直方图回答问题:(1)脉搏在 范围的学生最多,有 个人。 (2)脉搏在135---140有 人,160---165有 人,
(3) 全班有 人。
155~1601421149
描述数据?统计表;条形图;折线图;
扇形图.各方法有什么特点?条形统计图能清楚地表示出
每个项目的具体数目,便于
各项目进行比较。条形统计图扇形统计图能清楚地表示出
各部分在总体中所占的百分比.扇形统计图折线统计图能清楚地
反映数据的变化情况。折线统计图 为了参加全校各个年级之间的广播操比赛,七年级准备从63名同学中挑出身高相差不多的40名同学参加比赛.为此收集到这63名同学的身高(单位:cm)如下: 问题1问题1选择身高在哪个范围内的学生参加呢? 为了使选取的参赛选手身高比较整齐,需要知道数据的分布情况,即在哪些身高范围的学生比较多,哪些身高范围内的学生人数比较少.为此可以通过对这些数据适当分组来进行整理. 究竟分几组比较合适呢?原则上100个数以内分为5~12组较为恰当,且组数一定为正整数. 组数的多少由什么决定?总结:组数的多少由组距决定,组距越大组数越少,组距越小组数越多.对数据进行分析整理的步骤:1.计算最大值和最小值的差 在上面的数据中,最小值是149,
最大值是172,它们的差是23,说明身
高的变化范围是23 cm. 2.决定组距和组数
把所有数据分成若干组,每个小组的两
个端点之间的距离称为组距.(最大值-最小值)÷组距 所以要将数据分成8组:149≤x<152,152≤x<155,… 170≤x<173.这里组数和组距分别是8和3. 决定组数与组距的一般规律:数据越多,分得的
组数也越多。 假如数据总数为n
当n≤50时,则分为5 ~ 8组;
当50≤n≤100时,则分为8 ~ 12 组;
3.列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数(叫做频数).整理可以得到频数分布表,见教材146页表10-3. 从表中可以看出,身高在155≤x<158,158≤x<161,161≤x<164三个组的人数最多,一共有41人,因此可以从身高在155~164 cm(不含164 cm)的学生中选队员. ③列频数分布表;频数:落在各个小组内的数据个数。频数分布表已经能反映数据的分布特征。 有没有更直观的表示方法呢? 画频数分布直方图的步骤:(1)以横轴表示身高,纵轴表示频数与组数的比值.(3)在等距离分组中,由于小长方形的面积就是该组的频数,所以在作频数分布直方图时,小长方形的高完全可以用频数来代替.画出频数分布直方图频数/组距身高/㎝7
6
5
4
3
2
1
0149 152 155 158 161 164 167 170 173频数分布直方图 图10.2-2 4.画频数分布直方图
为了更直观形象地看出频数分布的情况,可以根据表格中的数据画出频数分布直方图. 频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小.小长方形的高是频数与组距的比值.
等距分组时,各个小长方形的面积(频数)与高的比是常数(组距),因此画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.画频数分布直方图的一般步骤:1、 计算最大值与最小值的差(极差).
2、决定组距与组数: 极差÷组距=组数
3、列频数分布表.
数出每一组频数
4、画频数分布直方图.
横轴表示各组数据,纵轴表示频数, 该组内的频数为高,画出一个个矩形。活动 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度(单位:cm)如下表:利用新知,解决实际问题解题过程:(1)计算最大与最小值的差. 在样本数据中,最大值是7.4,最小值是4.0,它们的差是7.4-4.0=3.4(cm)。利用新知,解决实际问题(2)决定组距和组数. 对数据分组整理的步骤:利用新知,解决实际问题(3)完成频数分布表 利用新知,解决实际问题 (4)画出频数分布直方图. 通过观察频数分布直方图,你发现了什么规律吗?利用新知,解决实际问题2、在对七年级某班的一次数学测验成绩进行统计分
析中,各分数段的人数如图所示(分数取正整数,满
分100分),请观察图形,并回答下列问题。(1)该班有 名学生;(2)70.5~80.5这一组的频数是 ,4414练习人数分数50.560.570.580.590.5100.52.根据直方图回答问题:(1)脉搏在 范围的学生最多,有 个人。 (2)脉搏在135---140有 人,160---165有 人,
(3) 全班有 人。
155~1601421149
