人教版数学九年级下册 27.1 图形的相似2 导学案无答案
文档属性
| 名称 | 人教版数学九年级下册 27.1 图形的相似2 导学案无答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-23 00:00:00 | ||
图片预览


文档简介
27.1 图形的相似 2
导学目标知识点:知道相似多边形的主要特征,即:相似多边形的对应角相等,对应边
的比相等;会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进
行相关的计算.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
1、观察图片,体会相似图形性质
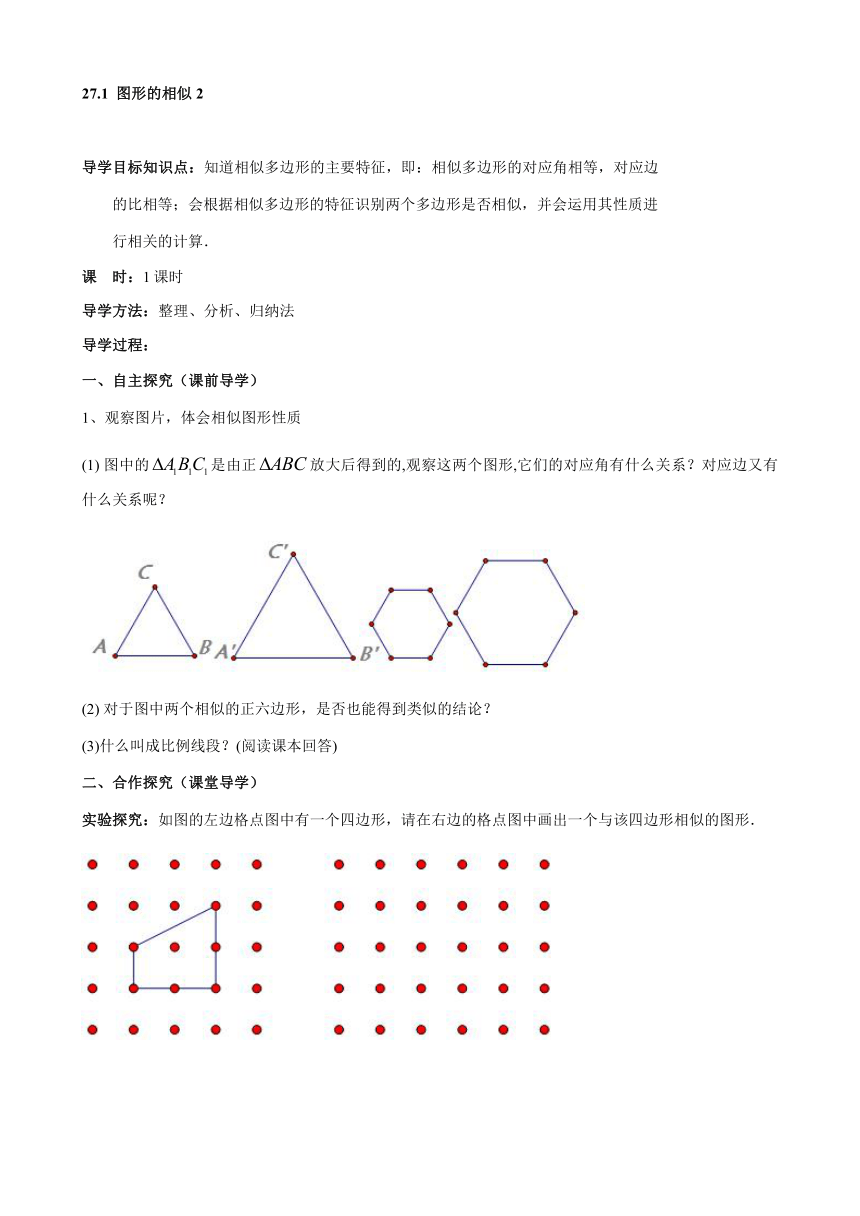
(1) 图中的是由正放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?
(2) 对于图中两个相似的正六边形,是否也能得到类似的结论?
(3)什么叫成比例线段?(阅读课本回答)
二、合作探究(课堂导学)
实验探究:如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
问题:对于图中两个相似的四边形,它们的对应角,对应边的比是否相等.
结论:
相似多边形的特征:相似多边形的对应角______,对应边的比_______.反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
几何语言:在和中
若.
则和相似
(2)相似比:相似多边形________的比称为相似比.
问题:相似比为1时,相似的两个图形有什么关系?
结论:相似比为1时,相似的两个图形______,因此________形是一种特殊的相似形.
例1下列说法正确的是( )
A.所有的平行四边形都相似 B.所有的矩形都相似
C.所有的菱形都相似 D.所有的正方形都相似
例2、如图,四边形和相似,求角的大小和EH的长度.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
已知四边形与四边形相似,
且,
若四边形的周长为40,求四边形的各边的长.
分析:因为两个四边形相似,因此可根据相似多边形的对应边的比相等来解题.
解:
拓展延伸(课外练习):
1.与相似,且相似比是,则 与与的相似比是( ).
A. B. C. D.
2.下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个 B.4个 C.5个 D.6个
3.在比例尺为1﹕10 000 000的地图上,量得甲、乙两地的距离是30 cm,求两地的实际距离.
4.如图所示的两个五边形相似,求未知边、、、的长度.
5.已知四边形和四边形相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形的最短边的长是6cm,那么四边形中最长的边长是多少?
6.如图,∥∥,,,若梯形与梯形相似,求的长.
7.如图,一个矩形ABCD的长AD=a cm,宽AB=b cm,E,F分别是AD,BC的中点,连接E,F,所得新矩形ABFE与原矩形ABCD相似,求的值.
课后反思:
小组评价: 教师评价:
导学目标知识点:知道相似多边形的主要特征,即:相似多边形的对应角相等,对应边
的比相等;会根据相似多边形的特征识别两个多边形是否相似,并会运用其性质进
行相关的计算.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
1、观察图片,体会相似图形性质
(1) 图中的是由正放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边又有什么关系呢?
(2) 对于图中两个相似的正六边形,是否也能得到类似的结论?
(3)什么叫成比例线段?(阅读课本回答)
二、合作探究(课堂导学)
实验探究:如图的左边格点图中有一个四边形,请在右边的格点图中画出一个与该四边形相似的图形.
问题:对于图中两个相似的四边形,它们的对应角,对应边的比是否相等.
结论:
相似多边形的特征:相似多边形的对应角______,对应边的比_______.反之,如果两个多边形的对应角______,对应边的比_______,那么这两个多边形_______.
几何语言:在和中
若.
则和相似
(2)相似比:相似多边形________的比称为相似比.
问题:相似比为1时,相似的两个图形有什么关系?
结论:相似比为1时,相似的两个图形______,因此________形是一种特殊的相似形.
例1下列说法正确的是( )
A.所有的平行四边形都相似 B.所有的矩形都相似
C.所有的菱形都相似 D.所有的正方形都相似
例2、如图,四边形和相似,求角的大小和EH的长度.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
已知四边形与四边形相似,
且,
若四边形的周长为40,求四边形的各边的长.
分析:因为两个四边形相似,因此可根据相似多边形的对应边的比相等来解题.
解:
拓展延伸(课外练习):
1.与相似,且相似比是,则 与与的相似比是( ).
A. B. C. D.
2.下列所给的条件中,能确定相似的有( )
(1)两个半径不相等的圆;(2)所有的正方形;(3)所有的等腰三角形;(4)所有的等边三角形;(5)所有的等腰梯形;(6)所有的正六边形.
A.3个 B.4个 C.5个 D.6个
3.在比例尺为1﹕10 000 000的地图上,量得甲、乙两地的距离是30 cm,求两地的实际距离.
4.如图所示的两个五边形相似,求未知边、、、的长度.
5.已知四边形和四边形相似,四边形ABCD的最长边和最短边的长分别是10cm和4cm,如果四边形的最短边的长是6cm,那么四边形中最长的边长是多少?
6.如图,∥∥,,,若梯形与梯形相似,求的长.
7.如图,一个矩形ABCD的长AD=a cm,宽AB=b cm,E,F分别是AD,BC的中点,连接E,F,所得新矩形ABFE与原矩形ABCD相似,求的值.
课后反思:
小组评价: 教师评价:
