2021-2022学年北师大版八年级数学上册第四章综合素质评价(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第四章综合素质评价(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-24 12:51:21 | ||
图片预览

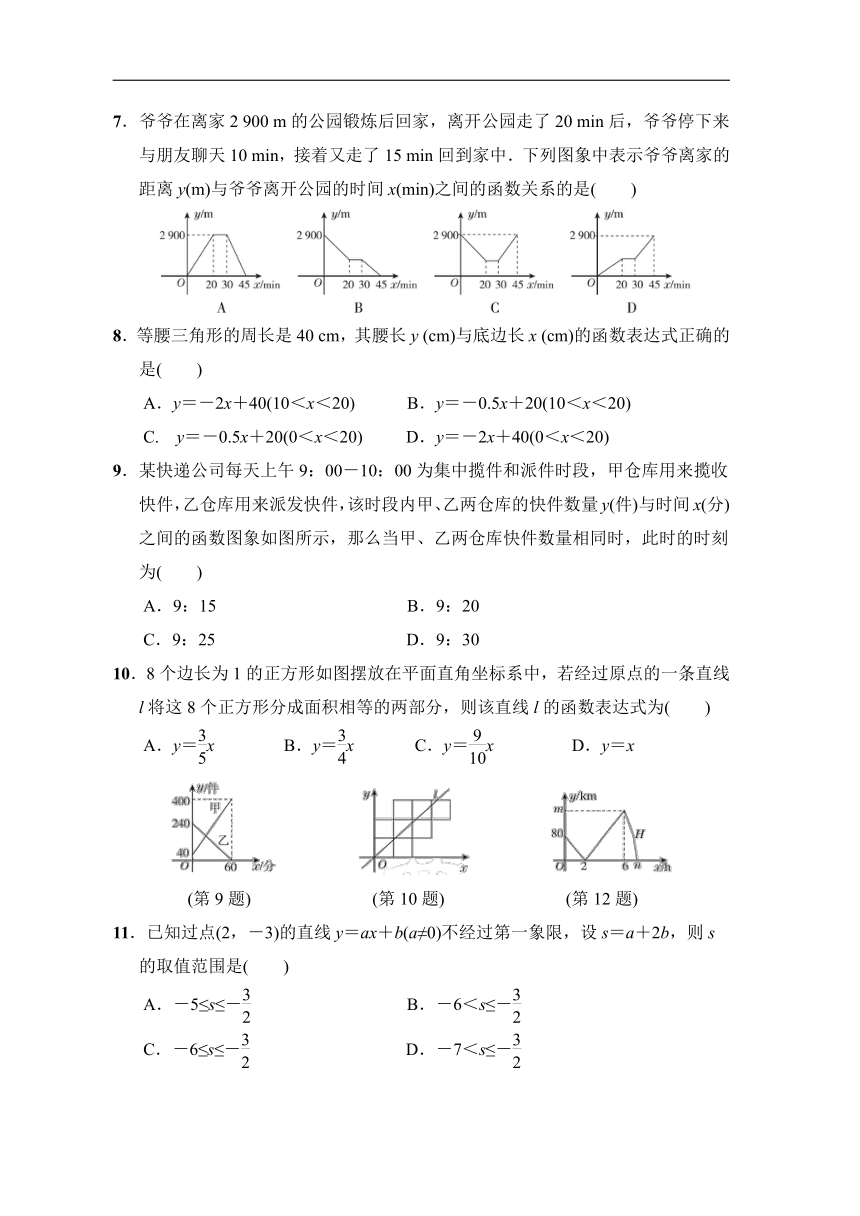



文档简介
第四章综合素质评价
一、选择题:本大题共12小题,每小题3分,共36分.在每小题列出的四个选项中,只有一个选项是符合题目要求的.
1.根据函数的定义,下列图象中表示函数的是( )
2.在函数y=-中,自变量x的取值范围是( )
A.x>-2 B.x≥-2
C.x>-2且x≠2 D.x≥-2且x≠2
3.已知某一次函数的图象与直线y=-2x+1平行,且过点(2,8),那么此一次函数的表达式为( )
A.y=-2x-2 B.y=-2x+12
C.y=-2x-6 D.y=-2x-12
4.对于一次函数y=-2x+4,下列结论正确的是( )
A.函数的图象不经过第三象限
B.函数的图象与x轴的交点坐标是(-2,0)
C.函数的图象向上平移4个单位长度后得到y=-2x的图象
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y2
5.两直线y1=kx+b和y2=bx+k(k≠0且b≠0)在同一平面直角坐标系内的图象位置可能是( )
6.一次函数y=(m-1)x+m的图象必过一定点,此定点的坐标为( )
A.(-1,1) B.(1,1)
C.(0,1) D.(1,-1)
7.爷爷在离家2 900 m的公园锻炼后回家,离开公园走了20 min后,爷爷停下来与朋友聊天10 min,接着又走了15 min回到家中.下列图象中表示爷爷离家的距离y(m)与爷爷离开公园的时间x(min)之间的函数关系的是( )
8.等腰三角形的周长是40 cm,其腰长y (cm)与底边长x (cm)的函数表达式正确的是( )
A.y=-2x+40(10<x<20) B.y=-0.5x+20(10<x<20)
C. y=-0.5x+20(0<x<20) D.y=-2x+40(0<x<20)
9.某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当甲、乙两仓库快件数量相同时,此时的时刻为( )
A.9:15 B.9:20
C.9:25 D.9:30
10.8个边长为1的正方形如图摆放在平面直角坐标系中,若经过原点的一条直线l将这8个正方形分成面积相等的两部分,则该直线l的函数表达式为( )
A.y=x B.y=x C.y=x D.y=x
(第9题) (第10题) (第12题)
11.已知过点(2,-3)的直线y=ax+b(a≠0)不经过第一象限,设s=a+2b,则s的取值范围是( )
A.-5≤s≤- B.-6<s≤-
C.-6≤s≤- D.-7<s≤-
12.甲、乙两车从A地出发,匀速驶向B地.甲车以80 km/h的速度行驶1 h后,乙车才沿相同路线行驶.乙车先到达B地并停留1 h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:
①乙车的速度是120 km/h;②m=160;③点H的坐标是(7,80);④n=7.4.
其中说法正确的有( )
A.1个 B.2 个 C.3个 D.4个
二、填空题:本大题共6小题,每小题4分,共24分.
13.如果函数y=(m-1)xm2-3是正比例函数,且y的值随x值的增大而增大,那么m的值是________.
14.一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是____________.
(第14题) (第18题)
15.点和点(2,n)在直线y=2x+b上,则m与n的大小关系是________.
16.2021年5月15日7时18分,“天问一号”火星探测器成功在火星着陆,开启了中国人自主探测火星之旅.已知华氏温度f(℉)与摄氏温度c(℃)之间的关系满足下表:
c/℃ … -10 0 10 20 30 …
f/℉ … 14 32 50 68 86 …
若火星上的平均温度大约为-55 ℃,则此温度换算成华氏温度约为 ____________℉.
17.某直线与x轴交于点A(-4,0),与y轴交于点B,若点B到x轴的距离为2,则该直线对应的函数表达式为__________________.
18.如图①所示,在长方形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y.如果y关于x的函数图象如图②所示,那么△ABC的面积是 ________.
三、解答题(一):本大题共2小题,每小题8分,共16分.
19.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求当x=-5时y的值.
20.拖拉机开始工作时,油箱中有油40 L,如果工作1 h耗油4 L,求:
(1)油箱中的余油量Q(L)与工作时间t(h)的函数关系式及自变量的取值范围;
(2)当工作5 h时油箱的余油量.
四、解答题(二):本大题共2小题,每小题10分,共20分.
21.如图,在平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l对应的函数表达式;
(2)若直线l上有一点P,使得S△ABP=S△AOB,求出点P的坐标.
22.甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2 h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题.
(1)乙车休息了________h;
(2)已知乙车与甲车相遇后y乙仍是x的正比例函数,求乙车与甲车相遇后y乙与x的函数表达式,并写出自变量x的取值范围;
(3)当甲、乙两车相距40 km时,求x值.
五、解答题(三):本大题共2小题,每小题12分,共24分.
23.某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的薪酬为y(元),原有的薪酬y1(元)计算方式采用的是底薪+提成,且y1=k1x+b1,已知每销售一件商品另外获得15元的提成.修改后的薪酬y2(元)计算方式为y2=k2x+b2.根据图象回答下列问题:
(1)分别求y1、y2与x之间的函数表达式,并说明b1和b2的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)请根据函数图象判断哪种薪酬计算方式更适合销售人员.
24.如图,直线y=-2x+8分别与x轴,y轴交于A,B两点,点C在线段AB上,过点C作CD⊥x轴于点D,CD=2OD,点E在线段OB上,且AE=BE.
(1)点C的坐标为 ________,点E的坐标为 ________;
(2)若直线m经过点E,且将△AOB分成面积比为1:2的两部分,求直线m的函数表达式;
(3)若点P在x轴上运动,当PC+PE取最小值时,求点P的坐标及PC+PE的最小值.
答案
一、1.C 2.D 3.B 4.A 5.A
6.A 点拨:将一次函数y=(m-1)x+m变形为
m(x+1)-x-y=0,
令x+1=0,
则-x-y=0,
解得x=-1,y=1,
故一次函数y=(m-1)x+m的图象必过定点(-1,1).
7.B
8.C 点拨:根据三角形周长的定义可得x+2y=40,
所以y=-0.5x+20.
又由三角形三边关系,
得x<2y,x>y-y,
所以x<2(-0.5x+20),x>0,
即x<20,x>0,
所以09.B 10.C
11.B 点拨:因为直线y=ax+b(a≠0)不经过第一象限,
所以a<0,b≤0.
因为直线y=ax+b(a≠0)过点(2,-3),
所以2a+b=-3,
所以a=,b=-2a-3,
所以s=a+2b=+2b=b-≤-,
s=a+2b=a+2(-2a-3)=-3a-6>-6,
所以s的取值范围是-6<s≤-.故选B.
12.D
二、13.2
14.x>0
15.m16.-67 点拨:由表中数据可得,
f=32+18×=32+1.8c,
当c=-55时,
f=32+1.8×(-55)=-67.
所以换算成华氏温度约为-67℉.
17.y=x+2或y=-x-2
18.10
三、19.解:(1)设y=k(x-1),
把x=3,y=4代入,得(3-1)k=4,
解得k=2,
所以y=2(x-1),即y=2x-2.
(2)当x=-5时,y=2×(-5)-2=-12.
20.解:(1)由题意可知Q=40-4t(0≤t≤10).
(2)把t=5代入Q=40-4t,
得Q=40-4×5=20.
所以当工作5 h时油箱的余油量为20 L.
四、21.解:(1)设直线l对应的函数表达式为y=kx,
把(6,4)代入,得4=6k,
解得k=.
所以直线l对应的函数表达式为y=x.
(2)因为A(6,4),B(12,0),
所以S△AOB=×12×4=24.
当S△ABP=S△AOB=8时,分两种情况,
设点P的坐标为.
①如图①,当点P在线段OA上时,连接BP,
则S△BOP=S△AOB-S△ABP=24-8=16,
即×12×x=16.
解得x=4,
则P;
②如图②,当点P在线段OA的延长线上时,连接BP,
则S△BOP=S△AOB+S△ABP=24+8=32,
即×12×x=32.
解得x=8,
则P.
故点P的坐标为或.
22.解:(1)0.5
(2)设乙车与甲车相遇后y乙与x的函数表达式为y乙=k2x,把(5,400)代入,得5k2=400.
解得k2=80.
所以y乙=80x(2.5≤x≤5).
(3)设乙车与甲车相遇前y乙与x的函数表达式为y乙=k3x,把(2,200)代入,得2k3=200.
解得k3=100.
所以乙车与甲车相遇前y乙与x的函数表达式为y乙=100x(0≤x≤2).
设y甲与x的函数表达式为y甲=k1x+b1.
把(0,400),(5,0)代入,
得b1=400,5k1+b1=0,
解得k1=-80,
所以y甲=-80x+400(0≤x≤5).
当0≤x≤2时,y甲-y乙=40,
即-80x+400-100x=40.
解得x=2.
当2.5≤x≤5时,y乙-y甲=40,
即80x-(-80x+400)=40.
解得x=.
所以当甲、乙两车相距40 km时,x=2或x=.
五、23.解:(1)因为y1=k1x+b1的图象过点(0,3 000),
所以b1=3 000,
又因为每销售一件商品另外获得15元的提成,
所以k1=15,
所以y1=15x+3 000.
因为y2=k2x+b2的图象过点(100,3 000),(0,0),
所以b2=0,100k2=3 000,
解得k2=30,
所以y2=30x.
所以b1的实际意义是底薪为3 000元,b2的实际意义是底薪为0元.
(2)令y1=y2,即15x+3 000=30x,
解得x=200,
所以y1=y2=6 000.
所以F(200,6 000),
所以交点F的实际意义是当销售人员一个月的销售量为200件时,销售人员通过两种薪酬计算方式所得的薪酬相等,为6 000元.
(3)结合函数图象可知,当0<x<200时,原有的薪酬计算方式更适合销售人员;当x=200时,两种薪酬计算方式对销售人员一样;当x>200时,修改后的薪酬计算方式更适合销售人员.
24.解:(1)(2,4);(0,3)
(2)设直线m的函数表达式为y=kx+3,根据k值的不同,可分为两种情况讨论:
①当k>0时,如图①,设直线m交AB于点F,过点F作
FH⊥y轴于点H.
当S△BEF=S△AOB时,
易知B(0,8),E(0,3),
所以BE=5,
所以=×,
解得FH=.
将x=代入y=-2x+8,得y=.
将点F的坐标代入y=kx+3,
得k=,
所以直线m的函数表达式为y=x+3;
②当k<0时,如图②,设直线m交OA于点N.
当S△OEN=S△AOB时,易知OE=3,
所以=×,
解得ON=.
将点N的坐标代入y=kx+3,
得k=-,
所以直线m的函数表达式为y=-x+3.
综上,直线m的函数表达式为y=x+3或y=-x+3.
(3)作点E关于x轴的对称点E′,连接 CE′交x轴于点P,此时PC+PE取最小值.易知点E′的坐标为(0,-3),
设直线CE′的函数表达式为y=nx-3,
将点C(2,4)的坐标代入,得n=,
所以y=x-3.
将y=0代入y=x-3,得x=,
所以点P的坐标为,
作E′G⊥CD交CD延长线于点G,
易知E′G=OD=2,CG=7,
所以PC+PE的最小值=CE′==.
一、选择题:本大题共12小题,每小题3分,共36分.在每小题列出的四个选项中,只有一个选项是符合题目要求的.
1.根据函数的定义,下列图象中表示函数的是( )
2.在函数y=-中,自变量x的取值范围是( )
A.x>-2 B.x≥-2
C.x>-2且x≠2 D.x≥-2且x≠2
3.已知某一次函数的图象与直线y=-2x+1平行,且过点(2,8),那么此一次函数的表达式为( )
A.y=-2x-2 B.y=-2x+12
C.y=-2x-6 D.y=-2x-12
4.对于一次函数y=-2x+4,下列结论正确的是( )
A.函数的图象不经过第三象限
B.函数的图象与x轴的交点坐标是(-2,0)
C.函数的图象向上平移4个单位长度后得到y=-2x的图象
D.若两点A(1,y1),B(3,y2)在该函数图象上,则y1<y2
5.两直线y1=kx+b和y2=bx+k(k≠0且b≠0)在同一平面直角坐标系内的图象位置可能是( )
6.一次函数y=(m-1)x+m的图象必过一定点,此定点的坐标为( )
A.(-1,1) B.(1,1)
C.(0,1) D.(1,-1)
7.爷爷在离家2 900 m的公园锻炼后回家,离开公园走了20 min后,爷爷停下来与朋友聊天10 min,接着又走了15 min回到家中.下列图象中表示爷爷离家的距离y(m)与爷爷离开公园的时间x(min)之间的函数关系的是( )
8.等腰三角形的周长是40 cm,其腰长y (cm)与底边长x (cm)的函数表达式正确的是( )
A.y=-2x+40(10<x<20) B.y=-0.5x+20(10<x<20)
C. y=-0.5x+20(0<x<20) D.y=-2x+40(0<x<20)
9.某快递公司每天上午9:00-10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当甲、乙两仓库快件数量相同时,此时的时刻为( )
A.9:15 B.9:20
C.9:25 D.9:30
10.8个边长为1的正方形如图摆放在平面直角坐标系中,若经过原点的一条直线l将这8个正方形分成面积相等的两部分,则该直线l的函数表达式为( )
A.y=x B.y=x C.y=x D.y=x
(第9题) (第10题) (第12题)
11.已知过点(2,-3)的直线y=ax+b(a≠0)不经过第一象限,设s=a+2b,则s的取值范围是( )
A.-5≤s≤- B.-6<s≤-
C.-6≤s≤- D.-7<s≤-
12.甲、乙两车从A地出发,匀速驶向B地.甲车以80 km/h的速度行驶1 h后,乙车才沿相同路线行驶.乙车先到达B地并停留1 h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:
①乙车的速度是120 km/h;②m=160;③点H的坐标是(7,80);④n=7.4.
其中说法正确的有( )
A.1个 B.2 个 C.3个 D.4个
二、填空题:本大题共6小题,每小题4分,共24分.
13.如果函数y=(m-1)xm2-3是正比例函数,且y的值随x值的增大而增大,那么m的值是________.
14.一次函数y=kx+b的图象如图所示,当y<5时,x的取值范围是____________.
(第14题) (第18题)
15.点和点(2,n)在直线y=2x+b上,则m与n的大小关系是________.
16.2021年5月15日7时18分,“天问一号”火星探测器成功在火星着陆,开启了中国人自主探测火星之旅.已知华氏温度f(℉)与摄氏温度c(℃)之间的关系满足下表:
c/℃ … -10 0 10 20 30 …
f/℉ … 14 32 50 68 86 …
若火星上的平均温度大约为-55 ℃,则此温度换算成华氏温度约为 ____________℉.
17.某直线与x轴交于点A(-4,0),与y轴交于点B,若点B到x轴的距离为2,则该直线对应的函数表达式为__________________.
18.如图①所示,在长方形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y.如果y关于x的函数图象如图②所示,那么△ABC的面积是 ________.
三、解答题(一):本大题共2小题,每小题8分,共16分.
19.已知y与x-1成正比例,且当x=3时,y=4.
(1)求y与x之间的函数表达式;
(2)求当x=-5时y的值.
20.拖拉机开始工作时,油箱中有油40 L,如果工作1 h耗油4 L,求:
(1)油箱中的余油量Q(L)与工作时间t(h)的函数关系式及自变量的取值范围;
(2)当工作5 h时油箱的余油量.
四、解答题(二):本大题共2小题,每小题10分,共20分.
21.如图,在平面直角坐标系中,直线l经过原点O和点A(6,4),经过点A的另一条直线交x轴于点B(12,0).
(1)求直线l对应的函数表达式;
(2)若直线l上有一点P,使得S△ABP=S△AOB,求出点P的坐标.
22.甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2 h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的距离分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题.
(1)乙车休息了________h;
(2)已知乙车与甲车相遇后y乙仍是x的正比例函数,求乙车与甲车相遇后y乙与x的函数表达式,并写出自变量x的取值范围;
(3)当甲、乙两车相距40 km时,求x值.
五、解答题(三):本大题共2小题,每小题12分,共24分.
23.某大型商场为了提高销售人员的积极性,对原有的薪酬计算方式进行了修改,设销售人员一个月的销售量为x(件),销售人员的薪酬为y(元),原有的薪酬y1(元)计算方式采用的是底薪+提成,且y1=k1x+b1,已知每销售一件商品另外获得15元的提成.修改后的薪酬y2(元)计算方式为y2=k2x+b2.根据图象回答下列问题:
(1)分别求y1、y2与x之间的函数表达式,并说明b1和b2的实际意义;
(2)求两个函数图象的交点F的坐标,并说明交点F的实际意义;
(3)请根据函数图象判断哪种薪酬计算方式更适合销售人员.
24.如图,直线y=-2x+8分别与x轴,y轴交于A,B两点,点C在线段AB上,过点C作CD⊥x轴于点D,CD=2OD,点E在线段OB上,且AE=BE.
(1)点C的坐标为 ________,点E的坐标为 ________;
(2)若直线m经过点E,且将△AOB分成面积比为1:2的两部分,求直线m的函数表达式;
(3)若点P在x轴上运动,当PC+PE取最小值时,求点P的坐标及PC+PE的最小值.
答案
一、1.C 2.D 3.B 4.A 5.A
6.A 点拨:将一次函数y=(m-1)x+m变形为
m(x+1)-x-y=0,
令x+1=0,
则-x-y=0,
解得x=-1,y=1,
故一次函数y=(m-1)x+m的图象必过定点(-1,1).
7.B
8.C 点拨:根据三角形周长的定义可得x+2y=40,
所以y=-0.5x+20.
又由三角形三边关系,
得x<2y,x>y-y,
所以x<2(-0.5x+20),x>0,
即x<20,x>0,
所以0
11.B 点拨:因为直线y=ax+b(a≠0)不经过第一象限,
所以a<0,b≤0.
因为直线y=ax+b(a≠0)过点(2,-3),
所以2a+b=-3,
所以a=,b=-2a-3,
所以s=a+2b=+2b=b-≤-,
s=a+2b=a+2(-2a-3)=-3a-6>-6,
所以s的取值范围是-6<s≤-.故选B.
12.D
二、13.2
14.x>0
15.m
f=32+18×=32+1.8c,
当c=-55时,
f=32+1.8×(-55)=-67.
所以换算成华氏温度约为-67℉.
17.y=x+2或y=-x-2
18.10
三、19.解:(1)设y=k(x-1),
把x=3,y=4代入,得(3-1)k=4,
解得k=2,
所以y=2(x-1),即y=2x-2.
(2)当x=-5时,y=2×(-5)-2=-12.
20.解:(1)由题意可知Q=40-4t(0≤t≤10).
(2)把t=5代入Q=40-4t,
得Q=40-4×5=20.
所以当工作5 h时油箱的余油量为20 L.
四、21.解:(1)设直线l对应的函数表达式为y=kx,
把(6,4)代入,得4=6k,
解得k=.
所以直线l对应的函数表达式为y=x.
(2)因为A(6,4),B(12,0),
所以S△AOB=×12×4=24.
当S△ABP=S△AOB=8时,分两种情况,
设点P的坐标为.
①如图①,当点P在线段OA上时,连接BP,
则S△BOP=S△AOB-S△ABP=24-8=16,
即×12×x=16.
解得x=4,
则P;
②如图②,当点P在线段OA的延长线上时,连接BP,
则S△BOP=S△AOB+S△ABP=24+8=32,
即×12×x=32.
解得x=8,
则P.
故点P的坐标为或.
22.解:(1)0.5
(2)设乙车与甲车相遇后y乙与x的函数表达式为y乙=k2x,把(5,400)代入,得5k2=400.
解得k2=80.
所以y乙=80x(2.5≤x≤5).
(3)设乙车与甲车相遇前y乙与x的函数表达式为y乙=k3x,把(2,200)代入,得2k3=200.
解得k3=100.
所以乙车与甲车相遇前y乙与x的函数表达式为y乙=100x(0≤x≤2).
设y甲与x的函数表达式为y甲=k1x+b1.
把(0,400),(5,0)代入,
得b1=400,5k1+b1=0,
解得k1=-80,
所以y甲=-80x+400(0≤x≤5).
当0≤x≤2时,y甲-y乙=40,
即-80x+400-100x=40.
解得x=2.
当2.5≤x≤5时,y乙-y甲=40,
即80x-(-80x+400)=40.
解得x=.
所以当甲、乙两车相距40 km时,x=2或x=.
五、23.解:(1)因为y1=k1x+b1的图象过点(0,3 000),
所以b1=3 000,
又因为每销售一件商品另外获得15元的提成,
所以k1=15,
所以y1=15x+3 000.
因为y2=k2x+b2的图象过点(100,3 000),(0,0),
所以b2=0,100k2=3 000,
解得k2=30,
所以y2=30x.
所以b1的实际意义是底薪为3 000元,b2的实际意义是底薪为0元.
(2)令y1=y2,即15x+3 000=30x,
解得x=200,
所以y1=y2=6 000.
所以F(200,6 000),
所以交点F的实际意义是当销售人员一个月的销售量为200件时,销售人员通过两种薪酬计算方式所得的薪酬相等,为6 000元.
(3)结合函数图象可知,当0<x<200时,原有的薪酬计算方式更适合销售人员;当x=200时,两种薪酬计算方式对销售人员一样;当x>200时,修改后的薪酬计算方式更适合销售人员.
24.解:(1)(2,4);(0,3)
(2)设直线m的函数表达式为y=kx+3,根据k值的不同,可分为两种情况讨论:
①当k>0时,如图①,设直线m交AB于点F,过点F作
FH⊥y轴于点H.
当S△BEF=S△AOB时,
易知B(0,8),E(0,3),
所以BE=5,
所以=×,
解得FH=.
将x=代入y=-2x+8,得y=.
将点F的坐标代入y=kx+3,
得k=,
所以直线m的函数表达式为y=x+3;
②当k<0时,如图②,设直线m交OA于点N.
当S△OEN=S△AOB时,易知OE=3,
所以=×,
解得ON=.
将点N的坐标代入y=kx+3,
得k=-,
所以直线m的函数表达式为y=-x+3.
综上,直线m的函数表达式为y=x+3或y=-x+3.
(3)作点E关于x轴的对称点E′,连接 CE′交x轴于点P,此时PC+PE取最小值.易知点E′的坐标为(0,-3),
设直线CE′的函数表达式为y=nx-3,
将点C(2,4)的坐标代入,得n=,
所以y=x-3.
将y=0代入y=x-3,得x=,
所以点P的坐标为,
作E′G⊥CD交CD延长线于点G,
易知E′G=OD=2,CG=7,
所以PC+PE的最小值=CE′==.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
