2021-2022学年北师大版八年级数学上册第一章勾股定理综合素质评价(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第一章勾股定理综合素质评价(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-24 13:03:46 | ||
图片预览



文档简介
第一章综合素质评价
一、选择题:本大题共12小题,每小题3分,共36分.在每小题列出的四个选项中,只有一个选项是符合题目要求的.
1.在△ABC中,AB=c,AC=b,BC=a,下列条件中不能判定△ABC为直角三角形的是( )
A.(c+b)(c-b)=a2 B.∠A+∠B=∠C
C.a=2,b=4,c=5 D.a:b:c=5:12:13
2.在Rt△ABC中,∠C=90°,AC=5,BC=12,则点C到AB的距离是( )
A. B. C.13 D.
3.【2022 广东揭阳期末】下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6
C.3,4,5 D.9,12,15
4.下列说法:
①如果直角三角形的两边长分别是6,8,那么斜边长必是10;
②如果a,b,c是一组勾股数,那么3a,3b,3c仍是勾股数;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a>b=c,那么a2:b2:c2=2:1:1.
其中正确的是( )
A.①② B.②③ C.③④ D.②④
5.如图,一棵大树在离地面6 m,11 m两处被折成三段,中间一段AB恰好与地面平行,大树顶部C落在离大树底部D13 m处,则大树折断前的高度是( )
A.15 m B.17 m C.19 m D.21 m
(第5题) (第7题)
6.亮亮准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.2 m远的水底,竹竿高出水面0.4 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.1.6 m B.2 m C.2.5 m D.3 m
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
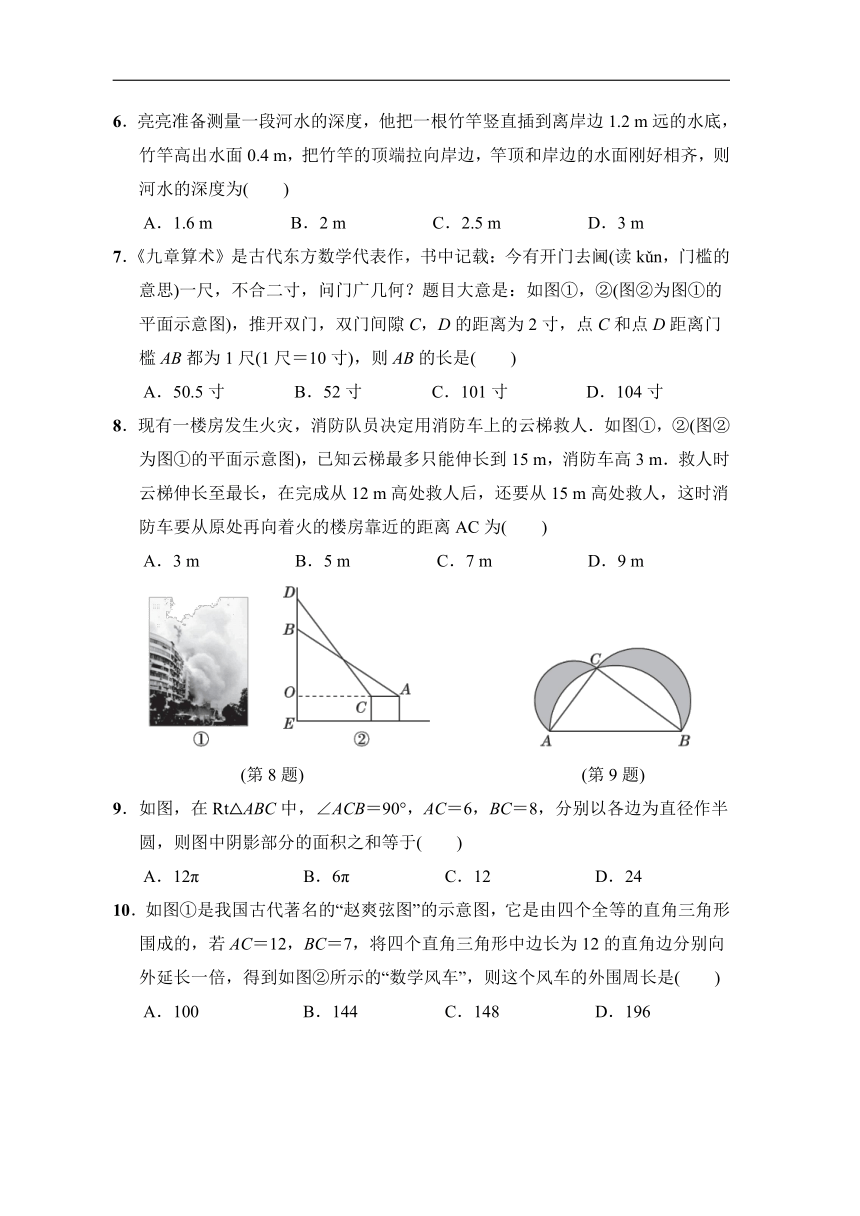
8.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人.如图①,②(图②为图①的平面示意图),已知云梯最多只能伸长到15 m,消防车高3 m.救人时云梯伸长至最长,在完成从12 m高处救人后,还要从15 m高处救人,这时消防车要从原处再向着火的楼房靠近的距离AC为( )
A.3 m B.5 m C.7 m D.9 m
(第8题) (第9题)
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,分别以各边为直径作半圆,则图中阴影部分的面积之和等于( )
A.12π B.6π C.12 D.24
10.如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个风车的外围周长是( )
A.100 B.144 C.148 D.196
(第10题) (第11题) (第12题)
11.如图,圆柱形容器的高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.3 m与蚊子相对的点A处,容器厚度忽略不计,则壁虎捕捉蚊子的最短路程为( )
A.1.3 m B.1.4 m C.1.5 m D.1.2 m
12.如图,P是等边三角形ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边在△ABC外作△AP′C≌△APB,连接PP′,则以下结论错误的是( )
A.△APP′是等边三角形 B.△PCP′是直角三角形
C.∠APB=150° D.∠APC=135°
二、填空题:本大题共6小题,每小题4分,共24分.
13.如图,在高为5 m,坡面长为13 m的楼梯表面铺地毯,地毯的长度至少需要 ________m.
(第13题) (第14题)
14.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,AC=3,则CD的长是 __________.
15.在△ABC中,AB=15,AC=20,D是BC所在直线上的点,AD=12,BD=9,则BC=____________.
16.观察下列勾股数组:①3,4,5;②5,12,13;③7,24,25;④9,40,41;….若a,144,145是其中的一组勾股数,则根据你发现的规律,a=________.
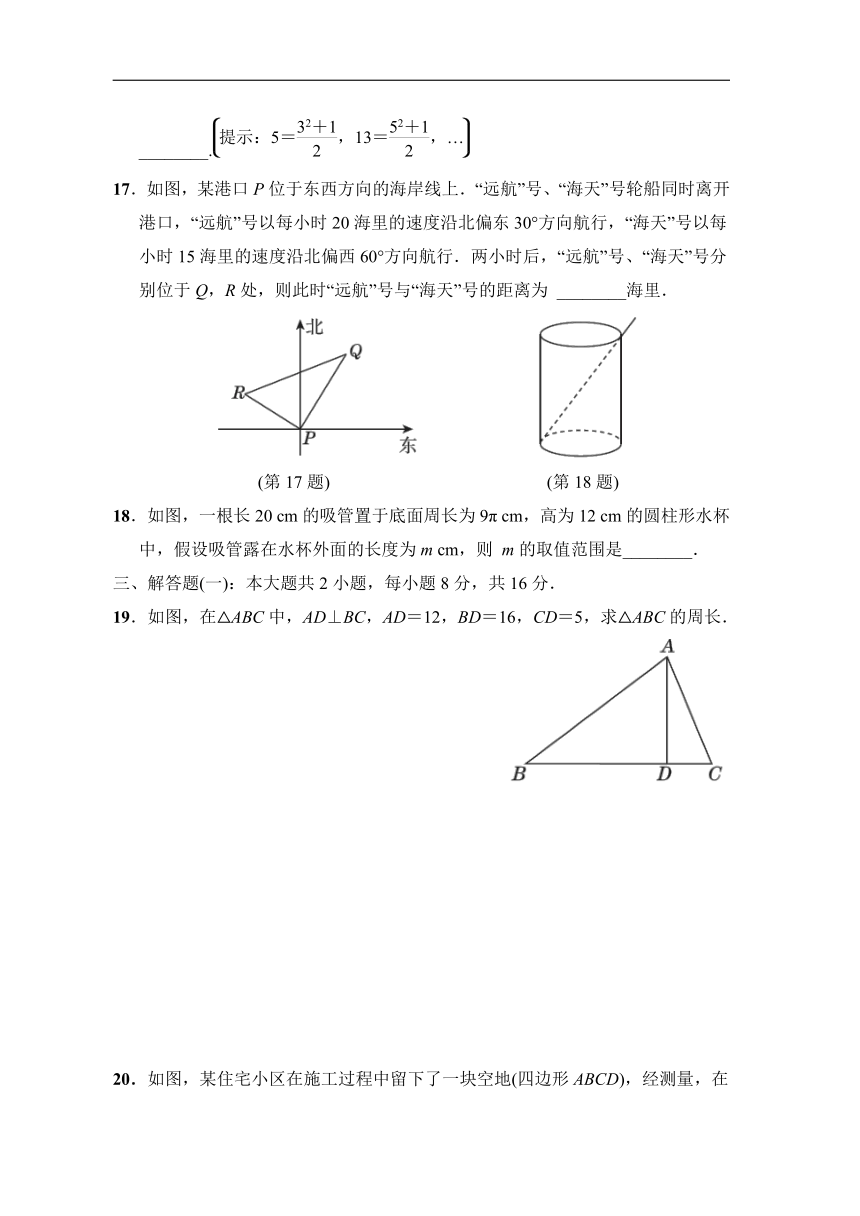
17.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,“远航”号以每小时20海里的速度沿北偏东30°方向航行,“海天”号以每小时15海里的速度沿北偏西60°方向航行.两小时后,“远航”号、“海天”号分别位于Q,R处,则此时“远航”号与“海天”号的距离为 ________海里.
(第17题) (第18题)
18.如图,一根长20 cm的吸管置于底面周长为9π cm,高为12 cm的圆柱形水杯中,假设吸管露在水杯外面的长度为m cm,则 m的取值范围是________.
三、解答题(一):本大题共2小题,每小题8分,共16分.
19.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求△ABC的周长.
20.如图,某住宅小区在施工过程中留下了一块空地(四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,铺满这块空地共需花费多少元?
四、解答题(二):本大题共2小题,每小题10分,共20分.
21.为了积极响应国家新农村建设的号召,某镇政府采用了移动宣讲的形式进行宣传动员.如图,在笔直公路MN的一侧点A处有一村庄,村庄到公路MN的距离为600 m(即AB=600 m),假设宣讲车P周围1 000 m以内(包含1 000 m)能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶.
(1)请问村庄能否听到广播宣传?说明理由.
(2)如果村庄能听到广播宣传,已知宣讲车P的速度是200 m/min,那么村庄总共能听到多长时间的广播宣传?
22.如图,在长方形ABCD中,AD∥BC,AB=4,BC=8.将长方形ABCD沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
五、解答题(三):本大题共2小题,每小题12分,共24分.
23.如图,直角三角形ABC和直角三角形DEF全等,顶点F在BC边上,顶点C,D重合,连接AE,EB,AB,DE交于点G,∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请回答以下问题:
(1)填空:∠AGE=________°.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
24.如图,在△ABC中,AB=AC=25 cm,BC=30 cm,BD⊥AC交AC于点D.动点P从点C出发,按C→A→B→C的路径运动,且速度为2 cm/s,设动点P的出发时间为t s.
(1)求边BC上的高;
(2)当动点P在BC边上运动时,若△CDP是以CD为腰的等腰三角形,请求出满足条件的t的值.
答案
一、1.C 2.B 3.B 4.D
5.D 点拨:如图,过点B作BO⊥DC于点O,
由题意,得AD=6m,
AB=5m,
易知BO=6 m,OD=5 m.
因为DC=13m,
所以OC=8m,
所以在Rt△BOC中,有
BC2=BO2+OC2,
所以BC=10 m.
所以大树折断前的高度为11+10=21(m).
6.A 点拨:设河水深x m,
则竹竿长为(x+0.4)m,
由题意,得x2+1.22=(x+0.4)2,
解得x=1.6,
所以河水的深度为1.6 m.
7.C 8.A
9.D 点拨:在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
所以AB2=AC2+BC2=100,
所以AB=10.
因为阴影部分的面积之和=两个小半圆的面积和-(大半圆的面积-△ABC的面积),
所以阴影部分的面积之和=π+π+S△ABC-π
=π+8π+24-π=24.
10.C 11.A 12.D
二、13.17 14.
15.25或7 点拨:如图①所示,当点D在线段BC上时,
因为AD=12,BD=9,AB=15,
所以AD2+BD2=AB2,
所以△ABD是直角三角形,且∠ADB=90°,
所以∠ADC=90°.
因为AC=20,
所以DC2=AC2-AD2=202-122=256,
所以DC=16,
所以BC=BD+CD=9+16=25;
如图②所示,当点D在线段CB的延长线上时,
同理可得DC=16,
所以BC=CD-BD=16-9=7;
由于AC>AB,所以点D不在线段BC的延长线上.
综上所述,BC的长度为25或7.
16.17
17.50
18.5≤m≤8
三、19.解:在Rt△ABD和Rt△ACD中,根据勾股定理,得
AB2=AD2+BD2,AC2=AD2+CD2.
因为AD=12,BD=16,CD=5,
所以AB=20,AC=13,
所以△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
20.解:如图,连接AC,
因为在△ABC中,AB=3 m,BC=4 m,∠B=90°,
所以AC=5 m.
在△ACD中,AC=5 m,CD=12 m,DA=13 m,
所以AC2+CD2=AD2,
所以△ACD是直角三角形,
所以S△ABC=×3×4=6 (m2),
S△ACD=×5×12=30 (m2),
所以S四边形ABCD=6+30=36 (m2),
36×30=1 080(元).
答:铺满这块空地共需花费1 080元.
四、21.解:(1)村庄能听到广播宣传.
理由:因为村庄到公路MN的距离为600 m,
600<1 000,
所以村庄能听到广播宣传.
(2)假设当宣讲车P行驶到点G时,村庄开始能听到广播宣传,行驶到点Q时,村庄刚好听不到广播宣传,连接AG,AQ,则AG=AQ=1 000m.
因为AB⊥MN,
所以BG=BQ.
在Rt△ABG中,
AB=600 m,AG=1 000 m,
所以BG=800 m,
所以GQ=1 600 m.
1 600÷200=8(min),
所以村庄总共能听到8min的广播宣传.
22.解:(1)△BEF是等腰三角形.
理由:因为ED∥FC,所以∠DEF=∠BFE.
根据折叠的性质,得∠DEF=∠BEF,
所以∠BEF=∠BFE.
过点B作BH⊥EF于点H,
所以∠BHE=∠BHF=90°.
因为BH=BH,
所以△BHE≌△BHF.
所以BE=BF.
所以△BEF是等腰三角形.
(2)因为长方形ABCD沿EF折叠后点B与点D重合,
所以BE=DE.
设BE=DE=x,
则AE=AD-DE=8-x.
在Rt△ABE中,AB2+AE2=BE2,
即42+(8-x)2=x2,
解得x=5,
所以BE=5,
由(1)知BE=BF,
所以BF=5,
所以△BEF的面积=×5×4=10.
五、23.解:(1)90
(2)因为∠AGE=90°,
所以S四边形ACBE=S△ACB+S△ABE=AB·DG+AB·EG=AB·(DG+EG)=AB·DE=c2.
又由题意知S四边形ACBE=S四边形ACFE+S△EFB=(AC+EF)·CF+BF·EF=(b+a)b+(a-b)·a=b2+ab+a2-ab=a2+b2,
所以c2=a2+b2,
所以 a2+b2=c2.
24.解:(1)如图,过点A作AH⊥BC于点H,
因为AB=AC,AH⊥BC,
所以BH=BC=15cm.
在Rt△ABH中,由勾股定理,得
AH2=AB2-BH2,所以AH=20 cm.
所以边BC上的高为20 cm.
(2)因为S△ABC=BC·AH=AC·BD,
BC=30 cm,AH=20 cm,AC=25 cm,
所以BD=24 cm.
在Rt△BDA中,AB=25 cm,BD=24 cm,
所以AD=7 cm.
所以CD=AC-AD=18cm.
因为动点P在BC边上,且△CDP是以CD为腰的等腰三角形,
所以分两种情况讨论:
①当CP=CD=18 cm时,
t=(25+25+30-18)÷2=31;
②当DC=DP时,如图,过点D作DF⊥BC于点F,
因为S△BDC=BD·CD=BC·DF,
所以DF== cm.
在Rt△CDF中,由勾股定理,得CF=cm.
因为CD=DP,DF⊥CP,
所以PC=2CF=cm,
所以t=(25+25+30-)÷2=29.2.
综上所述,满足条件的t的值为31或29.2.
一、选择题:本大题共12小题,每小题3分,共36分.在每小题列出的四个选项中,只有一个选项是符合题目要求的.
1.在△ABC中,AB=c,AC=b,BC=a,下列条件中不能判定△ABC为直角三角形的是( )
A.(c+b)(c-b)=a2 B.∠A+∠B=∠C
C.a=2,b=4,c=5 D.a:b:c=5:12:13
2.在Rt△ABC中,∠C=90°,AC=5,BC=12,则点C到AB的距离是( )
A. B. C.13 D.
3.【2022 广东揭阳期末】下列选项中不是勾股数的是( )
A.7,24,25 B.4,5,6
C.3,4,5 D.9,12,15
4.下列说法:
①如果直角三角形的两边长分别是6,8,那么斜边长必是10;
②如果a,b,c是一组勾股数,那么3a,3b,3c仍是勾股数;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a>b=c,那么a2:b2:c2=2:1:1.
其中正确的是( )
A.①② B.②③ C.③④ D.②④
5.如图,一棵大树在离地面6 m,11 m两处被折成三段,中间一段AB恰好与地面平行,大树顶部C落在离大树底部D13 m处,则大树折断前的高度是( )
A.15 m B.17 m C.19 m D.21 m
(第5题) (第7题)
6.亮亮准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.2 m远的水底,竹竿高出水面0.4 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.1.6 m B.2 m C.2.5 m D.3 m
7.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图①,②(图②为图①的平面示意图),推开双门,双门间隙C,D的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
8.现有一楼房发生火灾,消防队员决定用消防车上的云梯救人.如图①,②(图②为图①的平面示意图),已知云梯最多只能伸长到15 m,消防车高3 m.救人时云梯伸长至最长,在完成从12 m高处救人后,还要从15 m高处救人,这时消防车要从原处再向着火的楼房靠近的距离AC为( )
A.3 m B.5 m C.7 m D.9 m
(第8题) (第9题)
9.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,分别以各边为直径作半圆,则图中阴影部分的面积之和等于( )
A.12π B.6π C.12 D.24
10.如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=12,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,得到如图②所示的“数学风车”,则这个风车的外围周长是( )
A.100 B.144 C.148 D.196
(第10题) (第11题) (第12题)
11.如图,圆柱形容器的高为1.2 m,底面周长为1 m,在容器内壁离容器底部0.3 m的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器顶部0.3 m与蚊子相对的点A处,容器厚度忽略不计,则壁虎捕捉蚊子的最短路程为( )
A.1.3 m B.1.4 m C.1.5 m D.1.2 m
12.如图,P是等边三角形ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边在△ABC外作△AP′C≌△APB,连接PP′,则以下结论错误的是( )
A.△APP′是等边三角形 B.△PCP′是直角三角形
C.∠APB=150° D.∠APC=135°
二、填空题:本大题共6小题,每小题4分,共24分.
13.如图,在高为5 m,坡面长为13 m的楼梯表面铺地毯,地毯的长度至少需要 ________m.
(第13题) (第14题)
14.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,AC=3,则CD的长是 __________.
15.在△ABC中,AB=15,AC=20,D是BC所在直线上的点,AD=12,BD=9,则BC=____________.
16.观察下列勾股数组:①3,4,5;②5,12,13;③7,24,25;④9,40,41;….若a,144,145是其中的一组勾股数,则根据你发现的规律,a=________.
17.如图,某港口P位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,“远航”号以每小时20海里的速度沿北偏东30°方向航行,“海天”号以每小时15海里的速度沿北偏西60°方向航行.两小时后,“远航”号、“海天”号分别位于Q,R处,则此时“远航”号与“海天”号的距离为 ________海里.
(第17题) (第18题)
18.如图,一根长20 cm的吸管置于底面周长为9π cm,高为12 cm的圆柱形水杯中,假设吸管露在水杯外面的长度为m cm,则 m的取值范围是________.
三、解答题(一):本大题共2小题,每小题8分,共16分.
19.如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5,求△ABC的周长.
20.如图,某住宅小区在施工过程中留下了一块空地(四边形ABCD),经测量,在四边形ABCD中,AB=3 m,BC=4 m,CD=12 m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,铺满这块空地共需花费多少元?
四、解答题(二):本大题共2小题,每小题10分,共20分.
21.为了积极响应国家新农村建设的号召,某镇政府采用了移动宣讲的形式进行宣传动员.如图,在笔直公路MN的一侧点A处有一村庄,村庄到公路MN的距离为600 m(即AB=600 m),假设宣讲车P周围1 000 m以内(包含1 000 m)能听到广播宣传,宣讲车P在公路MN上沿PN方向行驶.
(1)请问村庄能否听到广播宣传?说明理由.
(2)如果村庄能听到广播宣传,已知宣讲车P的速度是200 m/min,那么村庄总共能听到多长时间的广播宣传?
22.如图,在长方形ABCD中,AD∥BC,AB=4,BC=8.将长方形ABCD沿EF折叠,使点D与点B重合,点C落在点G处.
(1)试判断△BEF的形状,并说明理由;
(2)求△BEF的面积.
五、解答题(三):本大题共2小题,每小题12分,共24分.
23.如图,直角三角形ABC和直角三角形DEF全等,顶点F在BC边上,顶点C,D重合,连接AE,EB,AB,DE交于点G,∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请回答以下问题:
(1)填空:∠AGE=________°.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
24.如图,在△ABC中,AB=AC=25 cm,BC=30 cm,BD⊥AC交AC于点D.动点P从点C出发,按C→A→B→C的路径运动,且速度为2 cm/s,设动点P的出发时间为t s.
(1)求边BC上的高;
(2)当动点P在BC边上运动时,若△CDP是以CD为腰的等腰三角形,请求出满足条件的t的值.
答案
一、1.C 2.B 3.B 4.D
5.D 点拨:如图,过点B作BO⊥DC于点O,
由题意,得AD=6m,
AB=5m,
易知BO=6 m,OD=5 m.
因为DC=13m,
所以OC=8m,
所以在Rt△BOC中,有
BC2=BO2+OC2,
所以BC=10 m.
所以大树折断前的高度为11+10=21(m).
6.A 点拨:设河水深x m,
则竹竿长为(x+0.4)m,
由题意,得x2+1.22=(x+0.4)2,
解得x=1.6,
所以河水的深度为1.6 m.
7.C 8.A
9.D 点拨:在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
所以AB2=AC2+BC2=100,
所以AB=10.
因为阴影部分的面积之和=两个小半圆的面积和-(大半圆的面积-△ABC的面积),
所以阴影部分的面积之和=π+π+S△ABC-π
=π+8π+24-π=24.
10.C 11.A 12.D
二、13.17 14.
15.25或7 点拨:如图①所示,当点D在线段BC上时,
因为AD=12,BD=9,AB=15,
所以AD2+BD2=AB2,
所以△ABD是直角三角形,且∠ADB=90°,
所以∠ADC=90°.
因为AC=20,
所以DC2=AC2-AD2=202-122=256,
所以DC=16,
所以BC=BD+CD=9+16=25;
如图②所示,当点D在线段CB的延长线上时,
同理可得DC=16,
所以BC=CD-BD=16-9=7;
由于AC>AB,所以点D不在线段BC的延长线上.
综上所述,BC的长度为25或7.
16.17
17.50
18.5≤m≤8
三、19.解:在Rt△ABD和Rt△ACD中,根据勾股定理,得
AB2=AD2+BD2,AC2=AD2+CD2.
因为AD=12,BD=16,CD=5,
所以AB=20,AC=13,
所以△ABC的周长=AB+AC+BC=AB+AC+BD+DC=20+13+16+5=54.
20.解:如图,连接AC,
因为在△ABC中,AB=3 m,BC=4 m,∠B=90°,
所以AC=5 m.
在△ACD中,AC=5 m,CD=12 m,DA=13 m,
所以AC2+CD2=AD2,
所以△ACD是直角三角形,
所以S△ABC=×3×4=6 (m2),
S△ACD=×5×12=30 (m2),
所以S四边形ABCD=6+30=36 (m2),
36×30=1 080(元).
答:铺满这块空地共需花费1 080元.
四、21.解:(1)村庄能听到广播宣传.
理由:因为村庄到公路MN的距离为600 m,
600<1 000,
所以村庄能听到广播宣传.
(2)假设当宣讲车P行驶到点G时,村庄开始能听到广播宣传,行驶到点Q时,村庄刚好听不到广播宣传,连接AG,AQ,则AG=AQ=1 000m.
因为AB⊥MN,
所以BG=BQ.
在Rt△ABG中,
AB=600 m,AG=1 000 m,
所以BG=800 m,
所以GQ=1 600 m.
1 600÷200=8(min),
所以村庄总共能听到8min的广播宣传.
22.解:(1)△BEF是等腰三角形.
理由:因为ED∥FC,所以∠DEF=∠BFE.
根据折叠的性质,得∠DEF=∠BEF,
所以∠BEF=∠BFE.
过点B作BH⊥EF于点H,
所以∠BHE=∠BHF=90°.
因为BH=BH,
所以△BHE≌△BHF.
所以BE=BF.
所以△BEF是等腰三角形.
(2)因为长方形ABCD沿EF折叠后点B与点D重合,
所以BE=DE.
设BE=DE=x,
则AE=AD-DE=8-x.
在Rt△ABE中,AB2+AE2=BE2,
即42+(8-x)2=x2,
解得x=5,
所以BE=5,
由(1)知BE=BF,
所以BF=5,
所以△BEF的面积=×5×4=10.
五、23.解:(1)90
(2)因为∠AGE=90°,
所以S四边形ACBE=S△ACB+S△ABE=AB·DG+AB·EG=AB·(DG+EG)=AB·DE=c2.
又由题意知S四边形ACBE=S四边形ACFE+S△EFB=(AC+EF)·CF+BF·EF=(b+a)b+(a-b)·a=b2+ab+a2-ab=a2+b2,
所以c2=a2+b2,
所以 a2+b2=c2.
24.解:(1)如图,过点A作AH⊥BC于点H,
因为AB=AC,AH⊥BC,
所以BH=BC=15cm.
在Rt△ABH中,由勾股定理,得
AH2=AB2-BH2,所以AH=20 cm.
所以边BC上的高为20 cm.
(2)因为S△ABC=BC·AH=AC·BD,
BC=30 cm,AH=20 cm,AC=25 cm,
所以BD=24 cm.
在Rt△BDA中,AB=25 cm,BD=24 cm,
所以AD=7 cm.
所以CD=AC-AD=18cm.
因为动点P在BC边上,且△CDP是以CD为腰的等腰三角形,
所以分两种情况讨论:
①当CP=CD=18 cm时,
t=(25+25+30-18)÷2=31;
②当DC=DP时,如图,过点D作DF⊥BC于点F,
因为S△BDC=BD·CD=BC·DF,
所以DF== cm.
在Rt△CDF中,由勾股定理,得CF=cm.
因为CD=DP,DF⊥CP,
所以PC=2CF=cm,
所以t=(25+25+30-)÷2=29.2.
综上所述,满足条件的t的值为31或29.2.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
