2.9 有理数的乘法 课件

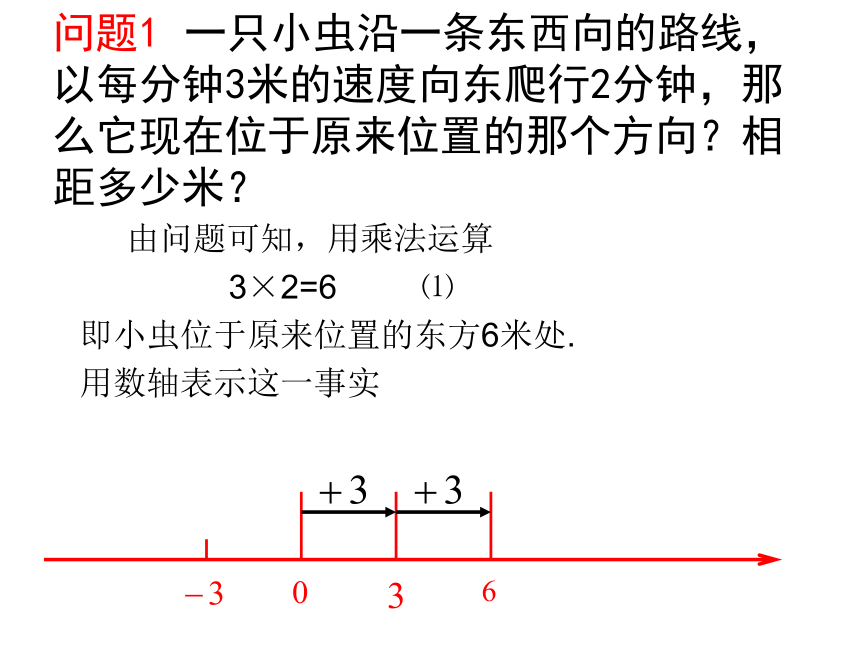
课件24张PPT。华东师大版 七年级上数学课件2.9有理数的乘法（第1课时）华东师大版七年级（上册）有理数的乘法法则问题1 一只小虫沿一条东西向的路线，以每分钟3米的速度向东爬行2分钟，那么它现在位于原来位置的那个方向？相距多少米？ 由问题可知，用乘法运算
3×2=6 ⑴
即小虫位于原来位置的东方6米处.
用数轴表示这一事实
问题2 一只小虫沿一条东西向的路线，以每分钟3米的速度向西爬行2分钟，那么它现在位于原来位置的那个方向？相距多少米？ 由问题可知，用乘法运算
（-3）×2=-6 ⑵
即小虫位于原来位置的西方6米处.
用数轴表示这一事实
3×2=6 ⑴
（-3）×2=-6 ⑵
你能从形式上比较⑴⑵的区别，并用语言表达如何从⑴式变为⑵式吗？
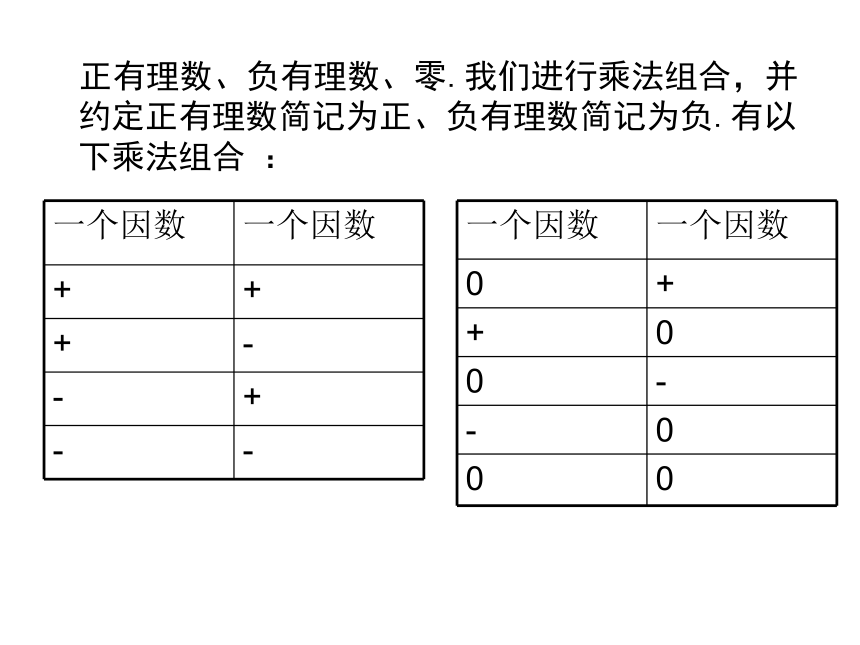
规律2： 两数相乘，若把一个因数换成它的相反数，则所得的积是原来的积的相反数. 正有理数、负有理数、零.我们进行乘法组合，并约定正有理数简记为正、负有理数简记为负.有以下乘法组合 ：


1.无零因数的有理数乘法⑴正有理数×正有理数 如：3×2=6 ⑴
⑵负有理数×正有理数
如：（-3）×2=-6 ⑵
⑶正有理数×负有理数
如：3 ×（-2）= ⑶
⑷负有理数×负有理数
如：（-3）×（-2）= ⑷
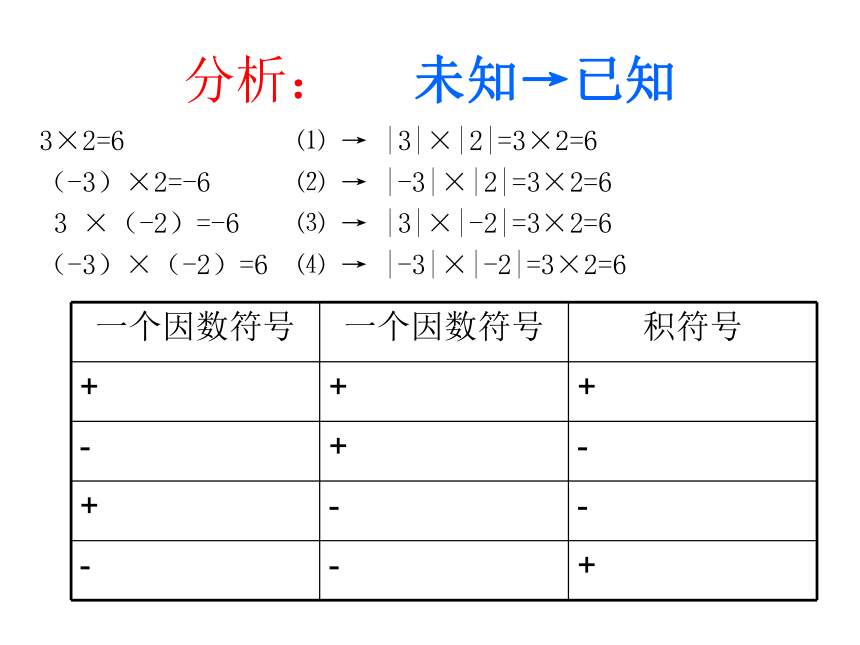
分析： 未知→已知3×2=6 ⑴ → |3|×|2|=3×2=6
（-3）×2=-6 ⑵ → |-3|×|2|=3×2=6
3 ×（-2）=-6 ⑶ → |3|×|-2|=3×2=6
（-3）×（-2）=6 ⑷ → |-3|×|-2|=3×2=6
归纳概括： 两数相乘，同号得正，异号得负，并把绝对值相乘.
2.有零因数的有理数乘法⑴零×正有理数
如：0×3=？
⑵正有理数×零
如：3×0=？
⑶零×负有理数
如：0 ×（-3）=？
⑷负有理数×零
如：（-3）×0=？
⑸零×零
0 ×0=？
00000归纳概括： 任何数与零相乘，都得零
有理数乘法法则：
两数相乘，同号得正，异号得负，并把绝对值相乘.
任何数与零相乘，都得零.

例1 计算
有理数的乘法运算律2.9 有理数的乘法（第2课时）诊断性测试一、回答下列问题二、计算下列各题1、5×（-6）2、（-6） × 53、 [ 3×（-4)] ×(-5)4、 3× [ （-4) ×(-5) ] 5、 5× [ 3 +(-7) ] 6、 5× 3+5 ×(-7) ] 练习一5×（-6）（-6） × 5=两个数相乘，交换因数的位置，积不变.练习二乘法结合律：（ab)c=a(bc)[ 3×（-4)] ×(-5)3× [ （-4) ×(-5) ] = 三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变。练习三5× [ 3 +(-7) ] 5× 3+5 ×(-7) ] =注意事项
(-10) × ×0.1×6
例2 计算：(-10) × ×0.1×6
= [(-10) ×0.1] ×
= (-1) ×2 = - 2
解：能直接写出下列各式的结果吗?
(-10) × ×0.1×6 =
(-10) × ×(-0.1)×6 =
(-10) × ×(-0.1)×( -6 )=
观察以上各式，能发现几个正数与负数相乘，积的符号与各因数的符号之间的关系吗?
一般地，我们有几个:不等于0的数相乘，积的符号由负因数的个数决定，当负因数有
奇数个时，积为负；当负因数有偶数个时，积为正.
几个不等于0的数相乘，首先确定积的符号，然后把绝对值相乘.
试一试：
几个数相乘，有一个因数为0，积就为0.
例4 计算：学以致用有理数乘法的运算律两个数相乘，交换因数的位置，积不变乘法交换律： ab=ba乘法结合律：（ab)c=a(bc) 根据乘法交换律和结合律可以推出：三个以上有理数相乘，可以任意交换因数的位置，也可先把其中的几个数相乘。 三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积不变。乘法分配律： a(b+c)=ab+ac 根据分配律可以推出：一个数同几个数的和相乘，等于把这个数分别同这几个数相乘，再把积相加。
一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。