3.4 整式的加减 5课时课件

课件77张PPT。华东师大版 七年级上数学课件§3.4 整式的加减
（第1课时）
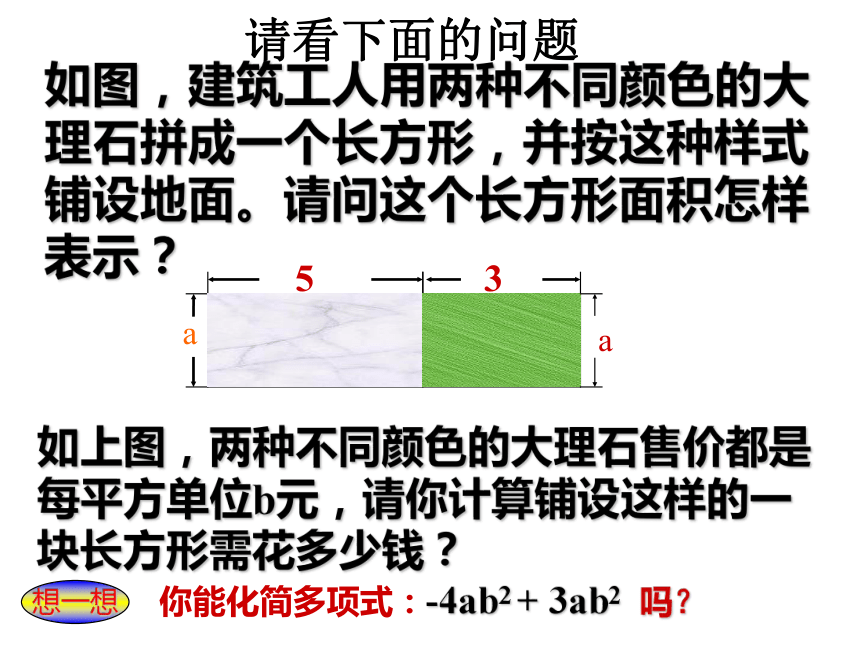
1.同 类 项 华东师大版七年级（上册）1.什么叫多项式？一、复习提问：2.什么叫多项式的项？ 周末，你一家要外出游玩，爸爸、 妈妈和你共选了以下要吃的东西：买的时候，你要怎么说？?通常我们会分类购买请看下面的问题如图，建筑工人用两种不同颜色的大理石拼成一个长方形，并按这种样式铺设地面。请问这个长方形面积怎样表示？你能化简多项式：-4ab2 + 3ab2 吗？想一想如上图，两种不同颜色的大理石售价都是每平方单位b元，请你计算铺设这样的一块长方形需花多少钱？问 题 探 讨1.各项所含字母相同；2.相同字母的指数分别相同；像 5a + 3a、 5ab + 3ab和 -4ab2 + 3ab2 多项式中的项，都可以合并成一项.你能发现这些能合并的项有什么特点吗？同类项：
所含字母相同，并且相同字母的指数也相等的项叫做同类项.
几个常数项也是同类项.1.同类项： 所含字母相同，并且相同字母的指数也
相等的项叫做同类项。几个常数项也是同类项。如：4x2+2y-3xy+7xy+3y-8x2-2同类项①字母相同 ②相同字母的指数也相等注：通常我们会用同一种符号表示同类项。2.同类项与系数大小无关；3.同类项与它们所含相同字母的顺序无关；议一议怎样判断同类项？1. 同类项有两个标准（1）所含字母相同；
（2）相同字母的指数分别相同；4.几个常数项也是同类项.1、下列各组中的两项是不是同类项？为什么？（1）2x2y与-3x2y （3）-3pq与3qp（2）2abc与2ab（4） -4x2y与5xy2 （√）（√）（×）（×） 问题征答议一议⑵ 已知2x2yn+1与 –3xmy4是同类项，
则 m = （ ），n = （ ）（1）下列各代数式中，是同类项的共有（ ）练习：(1)2x2y与5x2y;(2)0.2x2y与0.2xy2(3)- ab3与- ab3(4)4abc与4ab1.(抢答)下列各组中的两个项是不
是同类项？为什么？(5)mn与-mn(6) st与5ts是不是是不是是是2.指出下列多项式中的同类项(1)5x2y-3y2-x-4+x2y+2x-9；(2)4ab-7a2b2-8ab2+5a2b2-9ba+a2b2(7)12x3y2与-12x2y3(8)2x2与2x3(9)a3与53(10)-125与12不是不是不是是3.将下面的两个圈中的同类项用直线连结起来3x2y-24m5xy2 -a bb a-6y2x3-4x2ym课堂小结同 类 项课堂练习：P113 习 题 1、2、3数学有路练为径 (2)同类项与系数大小没有关系；
(3)同类项与所含相同字母的顺序
没有关系。注意： 一是所含字母相同，
二是相同字母的指数分别相同。两无关： (1)判断两个单项式(或多项式中的项)是不是同类项的条件：两相同五、小结同类项： 所含字母相同，并且相同字母的指数也分别相等的项你能找出多项式 4x2 + 2y - 3xy + 7 + 3y - 8x2 – 2 中的同类项吗？找 一 找再试试请指出下列多项式中的同类项：
3x3-2xy2+2-5xy-4y2x+xy-61.同类项： 所含字母相同，并且相同字母的指数也
相等的项叫做同类项。几个常数项也是同类项。如：4x2+2y-3xy+7+3y-8x2-2同类项①所含字母相同 ②相同字母的指数也相等注：通常我们会用同一种符号表示同类项。 你为家中买早餐，星期二买
了4根油条，2个烧饼，2碗豆浆；
星期三买了2根油条，3个烧饼，3
碗豆浆。你这两天一共为家里买
了多少早餐？我是小当家！　 生活中我们经常会根据
实际的需要把同类事物合并
起来。§3.4 整式的加减
（第2课时）
2.合并同类项 华东师大版七年级（上册）做一做（ ）（ ）根据乘法对加法的分配律把同类项合并成一项
叫做合并同类项乘法分配律乘法分配律的逆运用观察下列式子的变形，说明变形依据并填空根据以上的变形把下列各式中的同类项合并成一项合并同类项的法则　　把同类项的系数相加，所得的结果作为系数，字母和字母的指数保持不变。 你能用一句话把合并同类项的方法概括出来吗？例1：合并同类项－3x＋2y－5x－7y=(-3-5)x +(2-7)y 解:原式 =加法的交换律和结合律=（-8 ）x＋（-5）y（1） 合并同类项的法则有理数加法法则合并同类项步骤：1、找出同类项；2、把同类项写在一起；3、合并同类项。＋=－8x－5y（2）a2-3ab+5-a2-3ab-7解：原式＝(a2 – a2 )=( ) a2 +( ) ab+ ( )= - 6ab合并同类
项步骤：1、划线，找出同类项；2、把同类项写在一起；3、合并同类项。( –3ab–3ab )(5-7)1 - 1-3 – 3- 2-2 ++ 想一想： a2
怎么不见了？判别下列合并同类项是否正确辨一辨： 注：不是同类项
的不能合并练一练1.合并同类项例2.求多项式

的值，其中x=-3 反思与评价通过本节课你学到了什么？华东师大版七年级（上册）§3.4 整式的加减
（第3课时）
去括号一、复习：
1.什么叫同类项？你能举出几个同类项的
例子吗？
2.几个常数项是不是同类项？3.找出下列多项式中的同类项：
(1) 5a2b-3b2-a-4+a2b+2a-9；
(2) 4xy-7x2y2- 8xy2+ 5x2y2-9xy+ x2y2.去括号法则 精讲： 法则：括号前面是“+”号，把括号和它前面的“+”号去掉后，括号里的各项都不改变符号；括号前面是“-”号，把括号和它前面的“-”号去掉后，括号里的各项都要改变符号；例如：a+(b+c)=a+b+c
a-(b+c)=a-b-c对去括号法则的理解及注意事项如下：（1）去括号的依据是乘法分配律；（2）注意法则中“都”字，变号时，各项都要变，不是只变第一项；若不变号，各项都不变号；（3）有多重括号时，一般先去小括号，再去中括号，最后去大括号。每去掉一层括号，如果有同类项应随时合并，为下一步运算简便化，减少差错。“负”变“正”不变！！解：原式=a+b-c+d.解：原式=a-b+c-d.解：原式=m-n+p.例3、下列去括号对不对？为什么？
(1)a2-(2a-b+c)= a2-2a-b+c；
(2)a-(-b+c-d)=a+b+c-d；
(3)-(a-b)+(ab-1)=-a-b+ab-1；
(4)(m-n)-(m2- n2)=m-n+ m2+n2；
(5)a-[b-(c-d)]=a-b+(c-d).例4、先化简，再求值：
(1)3x+2-(2x+5),其中x=-65;
解：原式=3x+2-2x-5=x-3.当x=-65时，原式=-65-3=-68.§3.4 整式的加减
（第4课时）
添括号华东师大版七年级（上册） 热身运动（3）填空：
①　a-（-b-c）=__________ ，
②　x2-y2- 4（2x2-3y2）= _________
a+b+cx2-y2-8x2+12y2
1、复习提问：
（1）去括号法则是(2)合并同类项3a + (b – c)a – (–b + c)a + b – c = a + ( b – c)符号均没有变化 a + b – c = a – ( – b +c )符号均发生了变化+ ( )– ( )==a + b – ca + b – c
你能根据上面的分析总结出去括号的法则吗?所添的括号前面是“+”号，括到括号里的各项
都不改变正负号；
所添的括号前面是“－”号，括到括号里的各项
都改变正负号。 怎样检验添括号是否正确呢？检验方法：用去括号法则来检
验添括号是否正确做一做：
1.在括号内填入适当的项：
(1) x 2–x+1 = x 2 –( )；

(2) 2 x 2–3 x–1= 2 x 2 +( )；

(3)(a–b)–(c–d)= a –( ). x–1–3x–1b + c – d2.判断下面的添括号对不对：
(1) a2+2ab+b2=a2+(2ab+b2) ( )
(2) a2 – 2ab+b2=a2 – (2ab+b2) ( )
(3) a – b – c+d=(a+d) –(b – c) ( )
(4) (a – b+c)(– a+b+c)
=[+(a – b)+c][–(a – b)+c] ( )
=[c –(– a + b)][c+(– a + b)] ( ) 各显身手√ × × √ √ (1) 3x2 y2 – 2 x3 + y3
(2) – a3 + 2a2 – a +1
(3) 3x2 – 2xy2 + 2y23. 给下列多项式添括号，使括号内的最高次项系数为正数.如: – x2 + x = –(x2 – x); x2 – x = + (x2 – x)= +( )= –( )= –( )= –( )93x2 y2 – 2 x3 + y3a3 – 2a2 + a – 1– 3x2 + 2xy2 – 2y22xy2– 3x2 – 2y2你一定行4. 用简便方法计算：214a – 39a – 61a．7 解：214a – 39a – 61a=214a – (39a ＋ 61a)=214a – 100a=114a5. 化简求值：2x2y –3xy2 + 4x2y–5 xy2其中x＝1，y＝－1．解:2x2y –3xy2 + 4x2y–5 xy2=(2x2y + 4x2y) –(3xy2 + 5 xy2)=6x2y–8xy2当x＝1，y＝－1时原式=6×12×(–1)–8×1×( –1 )2= –6–8= –14智力大冲浪填空: 2xy2 – x3 – y3 + 3x2y
=+( )
= –( )
= 2xy2 – ( )+ 3x2y
= 2xy2 + ( )+ 3x2y
= 2xy2 – ( ) – x3 2xy2 – x3 – y3 + 3x2y– 2xy2 + x3 + y3 – 3x2yx3 + y3– x3 – y3y3 – 3x2y探索题 把多项式
１０ｘ３－７ｘ２ｙ＋４ｘｙ２＋２ｙ３－５
写成两个多项式的差，使被减数不含字母ｙ。（ 10x3-5）-（7x2y-4xy2-2y3）探索题 (2) 已知ｓ＋ｔ＝２１，３ｍ－２ｎ＝－１１求
（２ｓ＋９ｍ）＋［－（６ｎ－２ｔ）］的值 原式=2s+9m-6n+2t
=2（s+t）+3（3m-2n）
=2×21+3×（-11）
=9我们的收获……结合本堂课内容，请用下列句式造句。我学会了……
我明白了……
我认为……
我会用……
我想……3.4整式的加减（第5课时）
4.整式的加减华东师大版七年级（上册）复习提问大家还记得吗？1、（a-b)+(-c-d)=________
(a-b)-(-c-d)=________
2、-(a-b)+(-c-d)=_________
-(a-b)-(-c-d)=___________
3、a+b-c+d=a+( )=-( )+d
4、(a-b+c)(-a+b+c)=〔c-( )〕〔c+( )〕2大家会化简吗？先去括号再合并同类项概括： 不难发现，去括号和合并同类项是整式加减的基础。因此，整式加减一般步骤可以总结为
先去括号，再合并同类项
5大显身手例2计算若第一题中x=1,y=2这样就可以求出这个代数式的值。这就变成了化简求值。化简求值 6
例3整式加减的变式运用补充:a、b在数轴上的位置如图所示化简： 小结一、通过本堂课的学习 你知道了什么？二、整式加减的一般步骤是什么？
　　求代数式的值的一般步骤是什么？整 式 的 加 减复习华东师大版七年级（上册）例1.求整式x2-7x-2与-2x2+4x-1的差。 解：由题意得 (x2-7x-2)-(-2x2+4x-1)= x2 -7x –2 + 2x2 - 4x +1 = 3x2 -11x-1 2.计算：-2y3+(3xy2-x2y)-2(xy2-y3). 例3 化简求值:2x2y-3xy2+4x2y-5xy2,其中x=1,y=-1解： 2x2y-3xy2+4x2y-5xy2 =(2x2y+4x2y)+(-3xy2-5xy2)=6x2y-8xy2 当x=1，y=-1时， 原式=6×12×(-1)-8×1×(-1)2=-14 练一练：将代数式先化简，再求值：例4，完成下面各题 （1）已知x －y = 2,则6 －x + y值为———（2）已知m2 + m + 2的值为5时,则代数式
2m2 + 2m － 6的值为______练一练：已知2m2 - m +1的值为4,则代数式
6 － 4m2 + 2m 的值为______ 动物们要举行庆祝大会，兔妈妈受到邀请，准备了一个合唱的节目，兔妈妈想这样安排，第一排站n只兔子，从第二排起每排都比前一排多一只兔子，一共站了四排，请你帮它算一下兔妈妈一共需要多少只兔子？分析：第一排:n 只第二排:(n+1)只第三排:(n+2)只第四排:(n+3)只答：一共需要（4n+6)只兔子 教室里原有a位同学，后来有(b+2)位同学去打篮球，有(b+3)位同学去参加兴趣小组，问最后教室里还有多少人？解: a-(b+2)-(b+3) =a-b-2-b-3 =a-2b-5 答:最后教室里还有（ a-2b-5 ）人比一比(下面的题可以任意选做,做对按题加分)1.(8分)一矩形纸片的边长为a和b,剪去一部分后,剩余部分如图所示,则剩余部分的周长是( )
A.a+b B.2a+2b C.a+2b D.2a+b
2.(5分)计算(7m2 - 2m2 )的结果为( )
A.9m2 B. -9m2 C. 5m2 D.-5m2
3.(6分)当x=-3时,代数式3x-2x2+5+3x2-2x –5的值为( )
A.7 B. -6 C. -9 D. 6
4.(5分)3x与3x-3的差是( )
A.6x-3 B.-3 C.6x+3 D.3
5.(6分)右图是数值转换机,若输入的x的值
为-3,则输出的结果是( )
A. 18 B. -18 C.-27 D.27反思与评价通过本节课你学习,想一想得到了什么？再见