4.5 最基本的图形——点和线(共2课时)课件
文档属性
| 名称 | 4.5 最基本的图形——点和线(共2课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 945.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-31 11:04:59 | ||
图片预览








文档简介
课件30张PPT。华东师大版 七年级上数学课件
4.5 最基本的图形——点 和 线
华东师大版七年级(上册)(第1课时)点和线北斗七星点可以表示一个物体的位置拉紧的绳子直尺的边缘想一想:烛光尖端运动后形成的图形?A B用大写英文字母表示点1、表示为线段AB或线段BAa2、表示为线段a
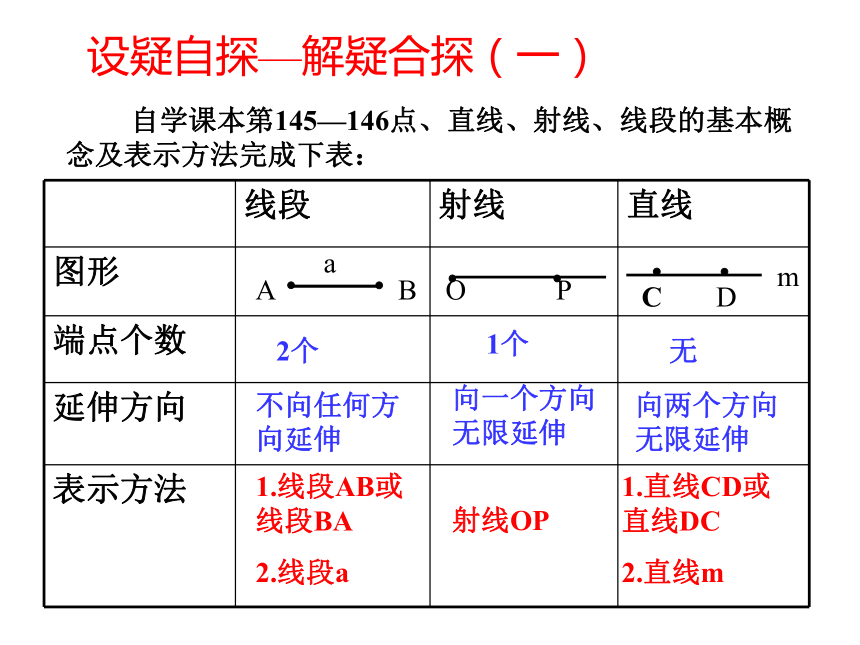
自学课本第145—146点、直线、射线、线段的基本概念及表示方法完成下表:设疑自探—解疑合探(一)2个1个无不向任何方向延伸向一个方向无限延伸向两个方向无限延伸1.线段AB或线段BA
2.线段a射线OP1.直线CD或直线DC
2.直线m? 如图:射线OA与射线OB是同一条射线吗?射线OB与射线AB是同一条射线吗?射线OA与射线AO是同一条射线吗?
说一说:注意:只有当两条射线的端点相同,方向也相同时才是同一条射线。判断题:
1、一条拉紧的线,就是直线。( )
2、直线的一半就是射线。( )
3、射线OA和射线AO是同一条射线。( )
4、线段AB和线段BA是同一条线段。( )
思考:1、点C和直线AB的位置关系是什么?
2、点A和直线AB的位置关系是什么?×××√填空题:
下图中共有 条线段,分别是( )
条射线 , 分别是( )
条直线,是( )
解:端点确定法:
以A为左端点的线段有:线段AB、AC、AD
以B为左端点的线段有:线段BC、BD
以C为左端点的线段有:线段CD
线段AB、AC、AD、BC、BD、CD68射线AN、AM、BN、BM、CN、CM、DN、DM1直线MN
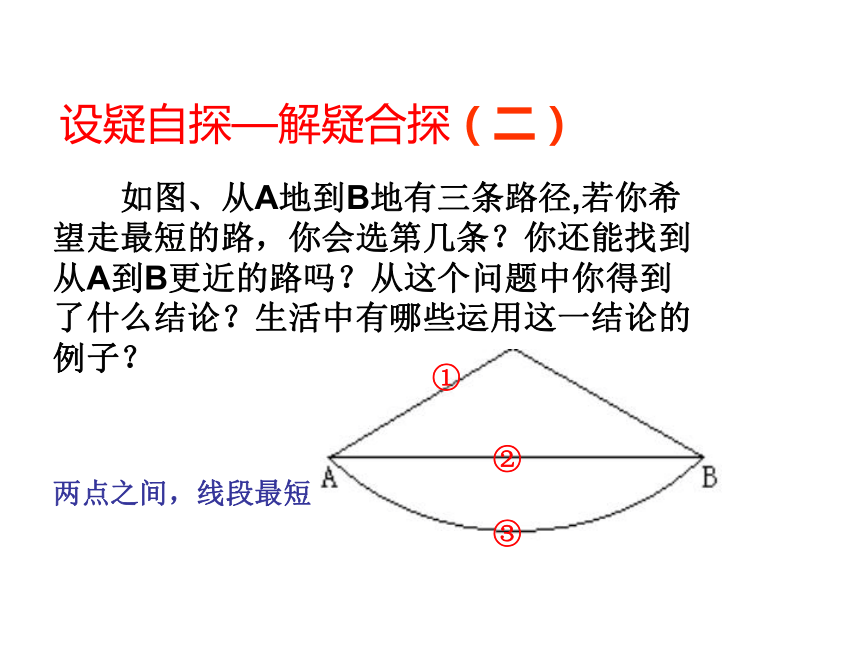
如图、从A地到B地有三条路径,若你希望走最短的路,你会选第几条?你还能找到从A到B更近的路吗?从这个问题中你得到了什么结论?生活中有哪些运用这一结论的例子? 设疑自探—解疑合探(二)①③②两点之间,线段最短两点间的距离:
两点之间线段的长度1、在纸上画一点A,过点A你能画几条直线?
2、 在纸上画一点A和一点B, 经过A、B两点画直线,你又可以画几条?由此你得出了什么结论?设疑自探—解疑合探(三)经过两点有一条直线,并且只有一条直线过一点可以画无数条直线思考:经过三点你可以画几条直线?
经过任意三点中的两点可以画出的直线的条数是多少?
反馈练习(三)下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着AB架设;
③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
④把弯曲的公路改直,就能缩短工程。
其中,可用“两点之间,线段最短”来解释的现象有( )
可用,过两点有且只有一条直线来解释的现象有( ) ① ③② ④ 本节课你有什么收获 ?还有什么不明白的地方? 小结反思 --质疑再探
生活拓展:
往返于甲、乙两地的客车,中途要停靠两个站.
问:1、有多少种不同的票价?
2、要准备多少种车票?
试一试线段的长短比较华东师大版七年级(上册)4.5 最基本的图形——点 和 线(第2课时)平面上有四个点,过其中每两个点画直线,
可以画几条?
解:设平面内四点为A,B,C,D。 (1)当A、B、C、D四个点在同一条直线上时,
可以画出 条直线。
(2)当A、B、C、D四个点中有三个点在同一
条直线上时,可以画出 条直线。
(3)当A、B、C、D四个点中任意三个点都不在
同一条直线上时,可以画出 条直线。
∴可以画出 条直线。 一四六一四六或或1、说出下列所示图形的名称及表示方法。(线段AB)(射线AB)(直线AB)A..B..AB2.判断正误
①延长直线AB到C( );
②反向延长射线AB到C( );
③延长线段AB到C( );
④直线a、b相交于一点m( );
⑤因为射线是直线的一半,
所以直线比射线长( );EABCDF3.如图,直线有 条, 分别是 ; 线段有 条, 分别是 ;
在直线EF上的射线有 条, 分别是 .线段的长短比较思考 :怎样比较两支铅笔的长短?
怎样比较两个同学的高矮? 比较两个同学高矮的方法:① 让两个同学站在同一平地上,脚底平齐, 观看两人的头顶,直接比出高矮;② 用卷尺分别度量出两个同学的身高,将 所得的数值进行比较。 ——度量法.——重合法试比较线段AB、CD的长短。..ABCD..(1) 度量法 用刻度尺量出线段AB长4cm,线段CD长4.5cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)(2) 重合法 将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。凭你的直觉比一比下列三组图形中线段a、b的长短ab( 1 )( 2 )ab( 3 )a用圆规作一条线段等于已知线段用圆规作一条线段等于已知线段MN。① 作射线AB;② 用圆规量出已知线段MN的长度;③ 在射线AB上以A为圆心, 截取AC = MN .CMN线 段 的 中 点 中点的概念 : 把一条线段分成两条相等的线段的点, 叫做这条线段的中点。(如图点C是线段AB的中点)C=如果AB = 4 cm,那么=2 cm例:如图AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么线段AD是多长呢?例题解析解:∵C点是AB的中点∴AC=CB==3cm∵ D点是BC的中点∴ CD= =1.5cm∴ AD=AC + CD=3 + 1.5=4.5cm计算已知,如图,点c在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,BC的中点,求线段MN的长度。A M C N B 再见
4.5 最基本的图形——点 和 线
华东师大版七年级(上册)(第1课时)点和线北斗七星点可以表示一个物体的位置拉紧的绳子直尺的边缘想一想:烛光尖端运动后形成的图形?A B用大写英文字母表示点1、表示为线段AB或线段BAa2、表示为线段a
自学课本第145—146点、直线、射线、线段的基本概念及表示方法完成下表:设疑自探—解疑合探(一)2个1个无不向任何方向延伸向一个方向无限延伸向两个方向无限延伸1.线段AB或线段BA
2.线段a射线OP1.直线CD或直线DC
2.直线m? 如图:射线OA与射线OB是同一条射线吗?射线OB与射线AB是同一条射线吗?射线OA与射线AO是同一条射线吗?
说一说:注意:只有当两条射线的端点相同,方向也相同时才是同一条射线。判断题:
1、一条拉紧的线,就是直线。( )
2、直线的一半就是射线。( )
3、射线OA和射线AO是同一条射线。( )
4、线段AB和线段BA是同一条线段。( )
思考:1、点C和直线AB的位置关系是什么?
2、点A和直线AB的位置关系是什么?×××√填空题:
下图中共有 条线段,分别是( )
条射线 , 分别是( )
条直线,是( )
解:端点确定法:
以A为左端点的线段有:线段AB、AC、AD
以B为左端点的线段有:线段BC、BD
以C为左端点的线段有:线段CD
线段AB、AC、AD、BC、BD、CD68射线AN、AM、BN、BM、CN、CM、DN、DM1直线MN
如图、从A地到B地有三条路径,若你希望走最短的路,你会选第几条?你还能找到从A到B更近的路吗?从这个问题中你得到了什么结论?生活中有哪些运用这一结论的例子? 设疑自探—解疑合探(二)①③②两点之间,线段最短两点间的距离:
两点之间线段的长度1、在纸上画一点A,过点A你能画几条直线?
2、 在纸上画一点A和一点B, 经过A、B两点画直线,你又可以画几条?由此你得出了什么结论?设疑自探—解疑合探(三)经过两点有一条直线,并且只有一条直线过一点可以画无数条直线思考:经过三点你可以画几条直线?
经过任意三点中的两点可以画出的直线的条数是多少?
反馈练习(三)下列四个生活、生产现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着AB架设;
③植树时,只要定出两棵树的位置,就能确定同一行所在的直线;
④把弯曲的公路改直,就能缩短工程。
其中,可用“两点之间,线段最短”来解释的现象有( )
可用,过两点有且只有一条直线来解释的现象有( ) ① ③② ④ 本节课你有什么收获 ?还有什么不明白的地方? 小结反思 --质疑再探
生活拓展:
往返于甲、乙两地的客车,中途要停靠两个站.
问:1、有多少种不同的票价?
2、要准备多少种车票?
试一试线段的长短比较华东师大版七年级(上册)4.5 最基本的图形——点 和 线(第2课时)平面上有四个点,过其中每两个点画直线,
可以画几条?
解:设平面内四点为A,B,C,D。 (1)当A、B、C、D四个点在同一条直线上时,
可以画出 条直线。
(2)当A、B、C、D四个点中有三个点在同一
条直线上时,可以画出 条直线。
(3)当A、B、C、D四个点中任意三个点都不在
同一条直线上时,可以画出 条直线。
∴可以画出 条直线。 一四六一四六或或1、说出下列所示图形的名称及表示方法。(线段AB)(射线AB)(直线AB)A..B..AB2.判断正误
①延长直线AB到C( );
②反向延长射线AB到C( );
③延长线段AB到C( );
④直线a、b相交于一点m( );
⑤因为射线是直线的一半,
所以直线比射线长( );EABCDF3.如图,直线有 条, 分别是 ; 线段有 条, 分别是 ;
在直线EF上的射线有 条, 分别是 .线段的长短比较思考 :怎样比较两支铅笔的长短?
怎样比较两个同学的高矮? 比较两个同学高矮的方法:① 让两个同学站在同一平地上,脚底平齐, 观看两人的头顶,直接比出高矮;② 用卷尺分别度量出两个同学的身高,将 所得的数值进行比较。 ——度量法.——重合法试比较线段AB、CD的长短。..ABCD..(1) 度量法 用刻度尺量出线段AB长4cm,线段CD长4.5cm,所以线段AB比线段CD短。(记作AB<CD 或 CD >AB)(2) 重合法 将一线段“移动”,使其一端点与另一线段的一端点重合,两线段的另一端点均在同一射线上。凭你的直觉比一比下列三组图形中线段a、b的长短ab( 1 )( 2 )ab( 3 )a用圆规作一条线段等于已知线段用圆规作一条线段等于已知线段MN。① 作射线AB;② 用圆规量出已知线段MN的长度;③ 在射线AB上以A为圆心, 截取AC = MN .CMN线 段 的 中 点 中点的概念 : 把一条线段分成两条相等的线段的点, 叫做这条线段的中点。(如图点C是线段AB的中点)C=如果AB = 4 cm,那么=2 cm例:如图AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么线段AD是多长呢?例题解析解:∵C点是AB的中点∴AC=CB==3cm∵ D点是BC的中点∴ CD= =1.5cm∴ AD=AC + CD=3 + 1.5=4.5cm计算已知,如图,点c在线段AB上,线段AC=6厘米,BC=4厘米,点M,N分别是AC,BC的中点,求线段MN的长度。A M C N B 再见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
