物理人教版(2019)选择性必修第一册1.3动量守恒定律(2)(共20张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.3动量守恒定律(2)(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-06-24 13:15:11 | ||
图片预览








文档简介
(共20张PPT)
动量守恒定律
动量守恒定律的运用
教学目标
1.知道动量守恒定律
2.能根据要求写出正确的动量守恒定律表达式
3.灵活运用动量守恒定律解决实际问题
重点 难点
灵活运用动量守恒定律解决实际问题
目录
01
动量守恒
02
动量守恒应用
03
典例
04
练习
上节课我们学习了动量守恒,知道动量守恒的条件以及动量守恒的三种常见表达式。下面我们一起复习上节课学的知识并运用动量守恒定律解决实际问题。
一、系统、内力和外力
1.系统:由两个(或多个)相互作用的物体构成的整体。
2.内力:系统中物体间的作用力。
3.外力:系统以外的物体施加给系统内物体的力。
二、动量守恒定律
1.内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变
2.条件:(1)系统不受外力或者所受外力的矢量和为0。(2)系统外力远小于内力时,外力的作用可以忽略,系统的动量守恒,如碰撞、爆炸系统。(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒
3.表达式:(1)m1v1+m2v2=m1v1'+m2v2
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(3)Δp=0
三、动量守恒定律四性 :(1)矢量性(2)系统性(3)相对性(4)普适性
四、应用动量守恒定律解题的基本步骤和方法
⑴分析题意,确定研究对象;
⑵分析作为研究对象的系统内各物体的受力情况,分清内力与外力,确定系统或某方向是否动量守恒;
⑶规定正方向,确定所研究的相互作用过程的始末状态,确定始、末状态的动量值的表达式;
⑷列动量守恒方程;
⑸求解.
弹簧小车
如图,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断线后,由于弹力作用,两辆小车分别向左、右运动,两小车与弹簧组成的系统动量是否守恒?
两小车在运动过程,弹簧弹力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
动量为矢量,矢量守恒,两小车的动量方向相反,动量的矢量和仍然为0
当小车速度相同时,弹簧弹性势能最大,小车相距最近;当弹簧处于原长时,小车速度最大。
A
B
C
v0
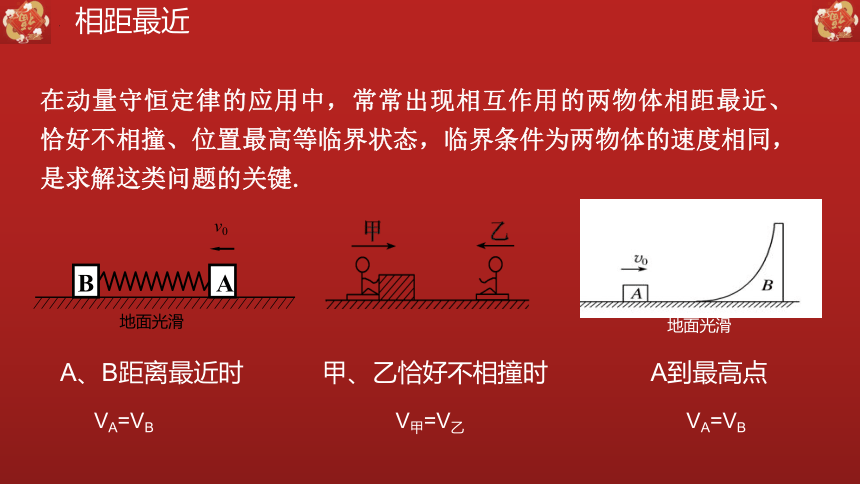
在动量守恒定律的应用中,常常出现相互作用的两物体相距最近、恰好不相撞、位置最高等临界状态,临界条件为两物体的速度相同,是求解这类问题的关键.
A
B
v0
地面光滑
地面光滑
VA=VB
VA=VB
V甲=V乙
A、B距离最近时
甲、乙恰好不相撞时
A到最高点
相距最近
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行,
①进入瞬间:合外力为零,系统动量守恒;合力功不为零,机械能不守恒
②一起滑行:合外力为零,动量不转移,系统动量守恒
若桌面粗糙①进入时:内力远大于外力,动量守恒,机械能不守恒
②一起滑行时:外力不能忽略,动量减少,系统动量不守恒
所以,从进入到一起滑行全程系统动量不变,求末速度时直接动量守恒
所以,求末速度时,先动量守恒后动能定理
子弹木块
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面粗糙、进入过程、子弹和木块系统动量怎样?
内力远大于外力(摩擦力)动量守恒
③桌面光滑、共速后、子弹和木块系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
(1)子弹和木块A动量_____,机械能_______.
A
B
(1)子弹和木块A动量________,机械能_______.
(2)子弹、木块A、木块B和弹簧动量______,机械能_______.
守恒
守恒
不守恒
不守恒
不守恒
守恒
子弹沿水平方向射入光滑水平桌面上的木块A后,一起压缩弹簧推动木块B直到弹簧最短。
A
B
A
B
处理方法:弹簧长度不变,B木块未动
子弹木块弹簧
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
斜面置于光滑水平面上,木块沿光滑斜面滑下。
斜面滑块
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车能持续地向右运动吗?说明理由.
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
铁锤小车的理解
如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯相对地面向上爬时,对于整个系统来说动量是否守恒 为什么
人、气球系统静止时,重力平衡浮力,合外力为零,人向上爬行时,相互作用内力变化,重力浮力未变, 系统动量守恒,任何一时刻系统动量矢量和必定都为零,当人向上运动,气球就向下运动。
如果整个系统开始一起加速上升状态,人往上爬行时,系统动量还守恒吗?
气球
一人站在静止于冰面的小车上,人与车的总质量M=70 kg,当它接到一个质量m=20 kg、以速度v0=5 m/s 迎面滑来的木箱后,立即以相对于自己v′=5 m/s的速度逆着木箱原来滑行的方向推出,不计冰面阻力。则小车获得的速度是多大?方向如何?
设推出木箱后小车的速度为v,此时木箱相对地面的速度为(v′-v),由动量守恒定律得
与木箱的初速度v0方向相同
典例
在光滑水平面上,有一质量M=3kg的薄板,板上有质量m=1kg的物块,两者以v0=4m/s的初速度朝相反方向运动,薄板与物块之间存在摩擦且薄板足够长,取水平向右为正方向,求:
(1)物块最后的速度;
(2)当物块的速度大小为3m/s时,薄板的速度。
(1)由于水平面光滑,物块与薄板组成的系统动量守恒,设共同运动速度大小为v,由动量守恒定律得
Mv0-mv0=(m+M)v
v=2m/s
(2)物块速度大小为3m/s时,方向向左,由动量守恒定律得
Mv0-mv0=-mv1+Mv′
v′=
m/s
方向水平向右。
如图所示,、B两个木块质量分别为与2kg,0.9kg、B与水平地面间接触光滑,上表面粗糙,质量为0.1kg的铁块以10m/s的速度从的左端向右滑动,最后铁块与B的共同速度大小为0.5m/s,铁块可视为质点,求:
(1)A的最终速度;
(2)铁块刚滑上B时铁块的速度。
(1)铁块从A的左端向右滑动,铁块做减速运动,A、B一起做加速运动,当铁块冲上B后,A、B分离,A做匀速运动,B继续做加速运动,当铁块与B达到共同速度后,一起做匀速运动。选铁块和木块A、B为系统,取水平向右为正方向,由系统总动量守恒得
代入数据解得
(2)设铁块刚滑上B时的速度为 ,此时A、B的速度均为 ,铁块与A、B组成的系统动量守恒,由系统动量守恒得
解得
如图所示,光滑水平轨道上放置长木板A(上表面粗糙)和滑块C,滑块B置于A的左端,三者质量分别为mA=2kg 、mB=1kg、mC=2kg .开始时C静止,A、B一起以v0 =5m/s的速度匀速向右运动,A与C发生碰撞(时间极短)后C向右运动,经过一段时间, A、B再次达到共同速度一起向右运动,且恰好不再与C碰撞.求A与C发生碰撞后瞬间A的速度大小.
谢谢观赏
动量守恒定律
动量守恒定律的运用
教学目标
1.知道动量守恒定律
2.能根据要求写出正确的动量守恒定律表达式
3.灵活运用动量守恒定律解决实际问题
重点 难点
灵活运用动量守恒定律解决实际问题
目录
01
动量守恒
02
动量守恒应用
03
典例
04
练习
上节课我们学习了动量守恒,知道动量守恒的条件以及动量守恒的三种常见表达式。下面我们一起复习上节课学的知识并运用动量守恒定律解决实际问题。
一、系统、内力和外力
1.系统:由两个(或多个)相互作用的物体构成的整体。
2.内力:系统中物体间的作用力。
3.外力:系统以外的物体施加给系统内物体的力。
二、动量守恒定律
1.内容:如果一个系统不受外力,或者所受外力的矢量和为0,这个系统的总动量保持不变
2.条件:(1)系统不受外力或者所受外力的矢量和为0。(2)系统外力远小于内力时,外力的作用可以忽略,系统的动量守恒,如碰撞、爆炸系统。(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒
3.表达式:(1)m1v1+m2v2=m1v1'+m2v2
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(3)Δp=0
三、动量守恒定律四性 :(1)矢量性(2)系统性(3)相对性(4)普适性
四、应用动量守恒定律解题的基本步骤和方法
⑴分析题意,确定研究对象;
⑵分析作为研究对象的系统内各物体的受力情况,分清内力与外力,确定系统或某方向是否动量守恒;
⑶规定正方向,确定所研究的相互作用过程的始末状态,确定始、末状态的动量值的表达式;
⑷列动量守恒方程;
⑸求解.
弹簧小车
如图,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断线后,由于弹力作用,两辆小车分别向左、右运动,两小车与弹簧组成的系统动量是否守恒?
两小车在运动过程,弹簧弹力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
动量为矢量,矢量守恒,两小车的动量方向相反,动量的矢量和仍然为0
当小车速度相同时,弹簧弹性势能最大,小车相距最近;当弹簧处于原长时,小车速度最大。
A
B
C
v0
在动量守恒定律的应用中,常常出现相互作用的两物体相距最近、恰好不相撞、位置最高等临界状态,临界条件为两物体的速度相同,是求解这类问题的关键.
A
B
v0
地面光滑
地面光滑
VA=VB
VA=VB
V甲=V乙
A、B距离最近时
甲、乙恰好不相撞时
A到最高点
相距最近
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行,
①进入瞬间:合外力为零,系统动量守恒;合力功不为零,机械能不守恒
②一起滑行:合外力为零,动量不转移,系统动量守恒
若桌面粗糙①进入时:内力远大于外力,动量守恒,机械能不守恒
②一起滑行时:外力不能忽略,动量减少,系统动量不守恒
所以,从进入到一起滑行全程系统动量不变,求末速度时直接动量守恒
所以,求末速度时,先动量守恒后动能定理
子弹木块
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面粗糙、进入过程、子弹和木块系统动量怎样?
内力远大于外力(摩擦力)动量守恒
③桌面光滑、共速后、子弹和木块系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
(1)子弹和木块A动量_____,机械能_______.
A
B
(1)子弹和木块A动量________,机械能_______.
(2)子弹、木块A、木块B和弹簧动量______,机械能_______.
守恒
守恒
不守恒
不守恒
不守恒
守恒
子弹沿水平方向射入光滑水平桌面上的木块A后,一起压缩弹簧推动木块B直到弹簧最短。
A
B
A
B
处理方法:弹簧长度不变,B木块未动
子弹木块弹簧
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
斜面置于光滑水平面上,木块沿光滑斜面滑下。
斜面滑块
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车能持续地向右运动吗?说明理由.
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
铁锤小车的理解
如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯相对地面向上爬时,对于整个系统来说动量是否守恒 为什么
人、气球系统静止时,重力平衡浮力,合外力为零,人向上爬行时,相互作用内力变化,重力浮力未变, 系统动量守恒,任何一时刻系统动量矢量和必定都为零,当人向上运动,气球就向下运动。
如果整个系统开始一起加速上升状态,人往上爬行时,系统动量还守恒吗?
气球
一人站在静止于冰面的小车上,人与车的总质量M=70 kg,当它接到一个质量m=20 kg、以速度v0=5 m/s 迎面滑来的木箱后,立即以相对于自己v′=5 m/s的速度逆着木箱原来滑行的方向推出,不计冰面阻力。则小车获得的速度是多大?方向如何?
设推出木箱后小车的速度为v,此时木箱相对地面的速度为(v′-v),由动量守恒定律得
与木箱的初速度v0方向相同
典例
在光滑水平面上,有一质量M=3kg的薄板,板上有质量m=1kg的物块,两者以v0=4m/s的初速度朝相反方向运动,薄板与物块之间存在摩擦且薄板足够长,取水平向右为正方向,求:
(1)物块最后的速度;
(2)当物块的速度大小为3m/s时,薄板的速度。
(1)由于水平面光滑,物块与薄板组成的系统动量守恒,设共同运动速度大小为v,由动量守恒定律得
Mv0-mv0=(m+M)v
v=2m/s
(2)物块速度大小为3m/s时,方向向左,由动量守恒定律得
Mv0-mv0=-mv1+Mv′
v′=
m/s
方向水平向右。
如图所示,、B两个木块质量分别为与2kg,0.9kg、B与水平地面间接触光滑,上表面粗糙,质量为0.1kg的铁块以10m/s的速度从的左端向右滑动,最后铁块与B的共同速度大小为0.5m/s,铁块可视为质点,求:
(1)A的最终速度;
(2)铁块刚滑上B时铁块的速度。
(1)铁块从A的左端向右滑动,铁块做减速运动,A、B一起做加速运动,当铁块冲上B后,A、B分离,A做匀速运动,B继续做加速运动,当铁块与B达到共同速度后,一起做匀速运动。选铁块和木块A、B为系统,取水平向右为正方向,由系统总动量守恒得
代入数据解得
(2)设铁块刚滑上B时的速度为 ,此时A、B的速度均为 ,铁块与A、B组成的系统动量守恒,由系统动量守恒得
解得
如图所示,光滑水平轨道上放置长木板A(上表面粗糙)和滑块C,滑块B置于A的左端,三者质量分别为mA=2kg 、mB=1kg、mC=2kg .开始时C静止,A、B一起以v0 =5m/s的速度匀速向右运动,A与C发生碰撞(时间极短)后C向右运动,经过一段时间, A、B再次达到共同速度一起向右运动,且恰好不再与C碰撞.求A与C发生碰撞后瞬间A的速度大小.
谢谢观赏
