三角形作辅助线的方法(无答案)
图片预览

文档简介
一、基础知识点:
1、在利用三角形三边关系证明线段不等关系时,若直接证不出来,可连接两点或延长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明。
典型例题
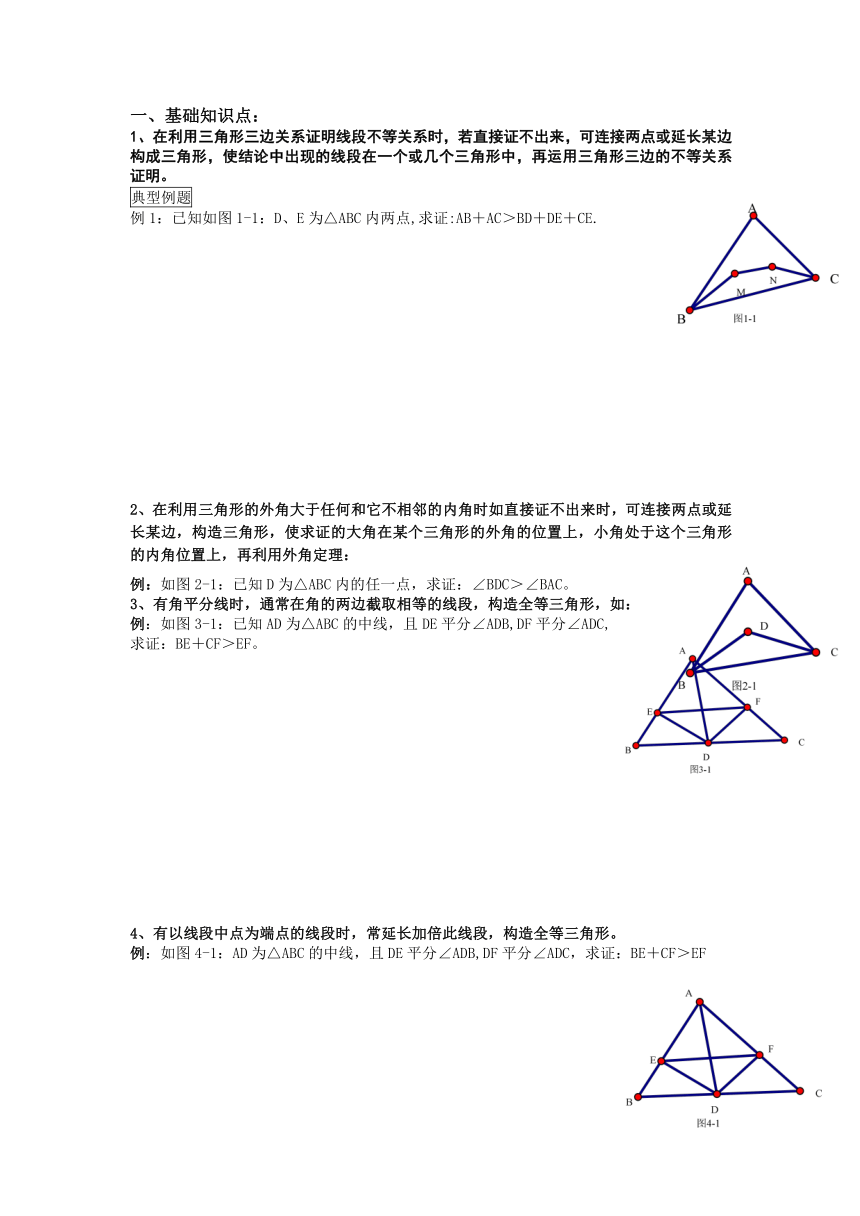
例1:已知如图1-1:D、E为△ABC内两点,求证:AB+AC>BD+DE+CE.
2、在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理:
例:如图2-1:已知D为△ABC内的任一点,求证:∠BDC>∠BAC。
3、有角平分线时,通常在角的两边截取相等的线段,构造全等三角形,如:
例:如图3-1:已知AD为△ABC的中线,且DE平分∠ADB,DF平分∠ADC,
求证:BE+CF>EF。
4、有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形。
例:如图4-1:AD为△ABC的中线,且DE平分∠ADB,DF平分∠ADC,求证:BE+CF>EF
5、有三角形中线时,常延长加倍中线,构造全等三角形。
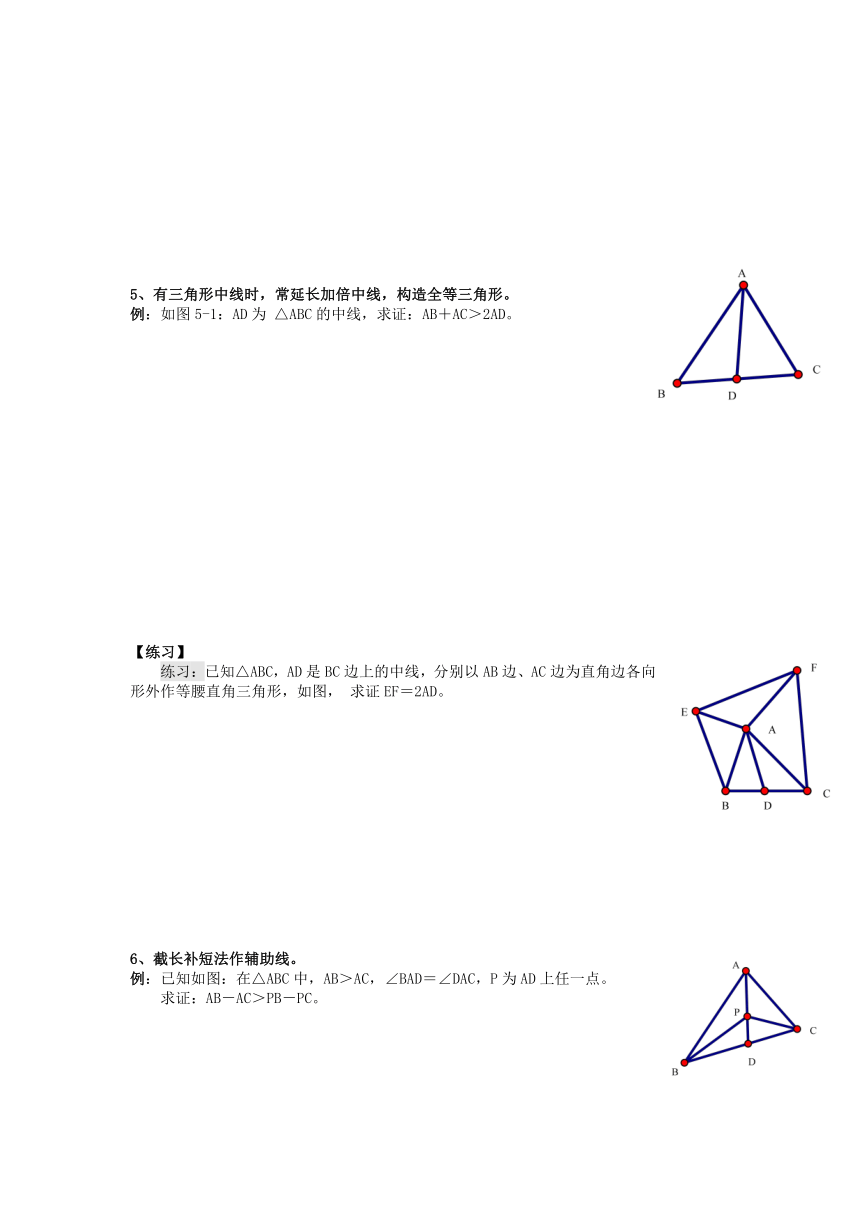
例:如图5-1:AD为 △ABC的中线,求证:AB+AC>2AD。
【练习】
练习:已知△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,如图, 求证EF=2AD。
6、截长补短法作辅助线。
例:已知如图:在△ABC中,AB>AC,∠BAD=∠DAC,P为AD上任一点。
求证:AB-AC>PB-PC。
7、延长已知边构造三角形:
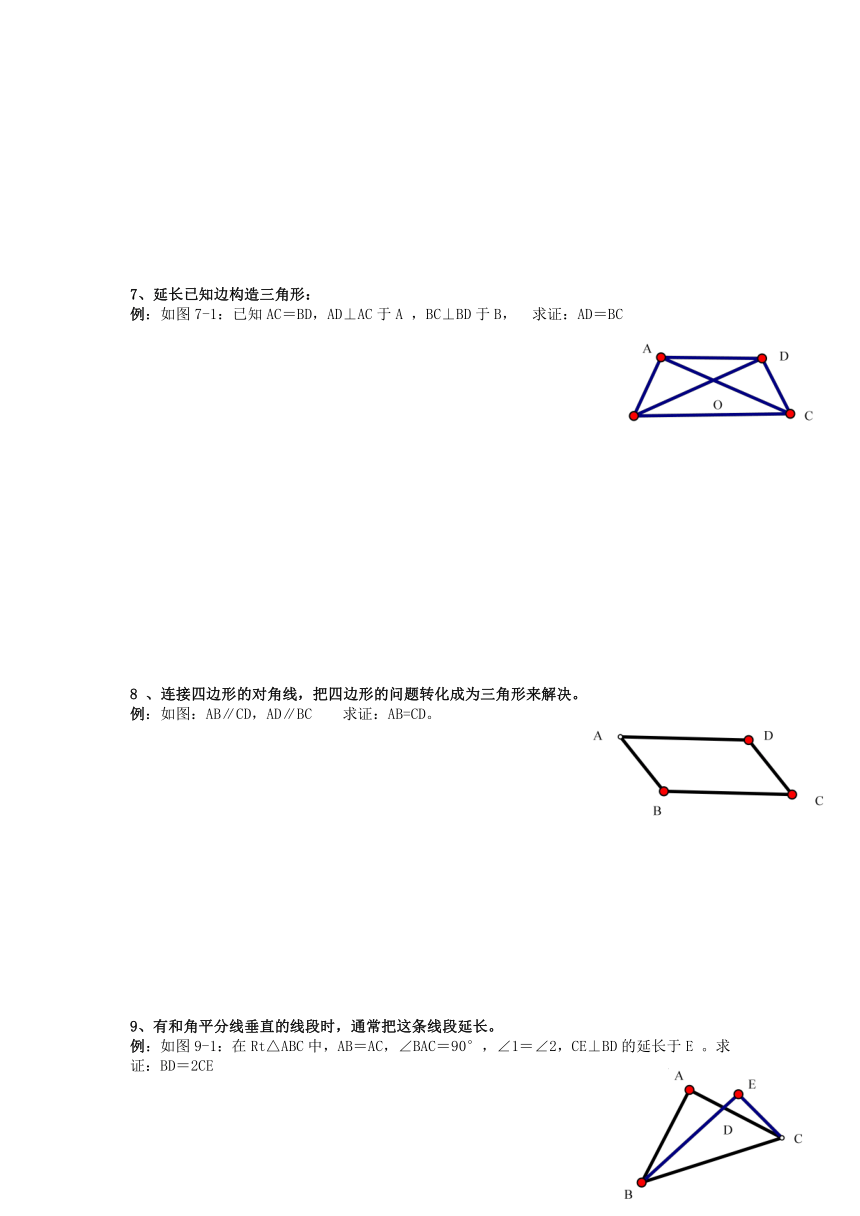
例:如图7-1:已知AC=BD,AD⊥AC于A ,BC⊥BD于B, 求证:AD=BC
8 、连接四边形的对角线,把四边形的问题转化成为三角形来解决。
例:如图:AB∥CD,AD∥BC 求证:AB=CD。
9、有和角平分线垂直的线段时,通常把这条线段延长。
例:如图9-1:在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长于E 。求证:BD=2CE
10、连接已知点,构造全等三角形。
例:已知:如图10-1;AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D。
11、取线段中点构造全等三有形。
例:如图11-1:AB=DC,∠A=∠D 求证:∠ABC=∠DCB。
12、利用三角形的三边关系求中线或高线的取值范围
已知两边,求第三边上的中线取值范围
例1、 已知在三角形ABC中,AB=10,BC=8,求第三边AC边上的中线BD的取值范围。
一般地:三角形的两边分别为a、b(a>b),则第三边上的中线p的取值范围是:(a-b)< p < (a+b)。
已知一边和另一边上的中线,求第三边的取值范围
例2 、在三角形ABC中,点D是BC边上的中点,AD=6,AB=7,求AC的取值范围。
已知两边上的高线,求第三边上的高线取值范围
例3、 已知三角形的两边上的高分别为4和6,求第三边上的高线的取值范围。
二、课前小测试:
1.如图(A),已知∠DAC=90,∠CBD=90,EF是△DEC的高,DA=CB,则全等的三角形有( )
A. 4对 B. 3对 C. 2对 D . 1对
2.已知如图(B),Rt△ABC中,∠ACB=90 ,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
A.AE=BE B. CE=AB C.∠CEB=2∠A D.AC=AB
3. 下列说法一定正确的是( )
A.三角形两边之和小于第三边 B.有一个角是锐角的三角形是锐角三角形
C.两边和一角对应相等的两个三角形全等 D.两角及一边对应相等的两个三角形全等
4. 下列对三角形中线说法不正确的是( )
A. 三角形的一条中线将这个三角形的一个角平分成相等的两个角.
B三角形的一条中线将这个三角形平分成面积相等的两个三角形.
C. 三角形的中线是连接一个顶点和它对边中点的线段.
D. 三角形的中线是线段,并交于一点.
5. 锐角三角形中任意两角之和一定大于( )
A.120 B.110 C.100 D.90
三、课后练习
1 、如图,已知△ABC中,AD是△ABC的中线,AB=8,AC=6,求AD的取值范围.
2、 如图,已知△ABC中,AB=AC,D在AB上,E是AC延长线上一点,且BD=CE,DE与BC交于点F. 求证:DF=EF.
3、 如图,已知RT△ACB中,∠C=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于E.
求证:BD=DE=CE.
4 、如图,已知△ABC中,∠B=2∠C,AD平分∠BAC交BC于D.
求证:AC=AB+BD.
5、如图,已知CE、CB分别是△ABC和△ADC的中线,且AB=AC.求证:CD=2CE.
6、 如图,已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE.求证:AB=AC,AD=AE.
7、 如图,在△ABC中,BD=DC,ED⊥DF.求证:BE+CF>EF.
图(B)
图(A)
1、在利用三角形三边关系证明线段不等关系时,若直接证不出来,可连接两点或延长某边构成三角形,使结论中出现的线段在一个或几个三角形中,再运用三角形三边的不等关系证明。
典型例题
例1:已知如图1-1:D、E为△ABC内两点,求证:AB+AC>BD+DE+CE.
2、在利用三角形的外角大于任何和它不相邻的内角时如直接证不出来时,可连接两点或延长某边,构造三角形,使求证的大角在某个三角形的外角的位置上,小角处于这个三角形的内角位置上,再利用外角定理:
例:如图2-1:已知D为△ABC内的任一点,求证:∠BDC>∠BAC。
3、有角平分线时,通常在角的两边截取相等的线段,构造全等三角形,如:
例:如图3-1:已知AD为△ABC的中线,且DE平分∠ADB,DF平分∠ADC,
求证:BE+CF>EF。
4、有以线段中点为端点的线段时,常延长加倍此线段,构造全等三角形。
例:如图4-1:AD为△ABC的中线,且DE平分∠ADB,DF平分∠ADC,求证:BE+CF>EF
5、有三角形中线时,常延长加倍中线,构造全等三角形。
例:如图5-1:AD为 △ABC的中线,求证:AB+AC>2AD。
【练习】
练习:已知△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,如图, 求证EF=2AD。
6、截长补短法作辅助线。
例:已知如图:在△ABC中,AB>AC,∠BAD=∠DAC,P为AD上任一点。
求证:AB-AC>PB-PC。
7、延长已知边构造三角形:
例:如图7-1:已知AC=BD,AD⊥AC于A ,BC⊥BD于B, 求证:AD=BC
8 、连接四边形的对角线,把四边形的问题转化成为三角形来解决。
例:如图:AB∥CD,AD∥BC 求证:AB=CD。
9、有和角平分线垂直的线段时,通常把这条线段延长。
例:如图9-1:在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长于E 。求证:BD=2CE
10、连接已知点,构造全等三角形。
例:已知:如图10-1;AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D。
11、取线段中点构造全等三有形。
例:如图11-1:AB=DC,∠A=∠D 求证:∠ABC=∠DCB。
12、利用三角形的三边关系求中线或高线的取值范围
已知两边,求第三边上的中线取值范围
例1、 已知在三角形ABC中,AB=10,BC=8,求第三边AC边上的中线BD的取值范围。
一般地:三角形的两边分别为a、b(a>b),则第三边上的中线p的取值范围是:(a-b)< p < (a+b)。
已知一边和另一边上的中线,求第三边的取值范围
例2 、在三角形ABC中,点D是BC边上的中点,AD=6,AB=7,求AC的取值范围。
已知两边上的高线,求第三边上的高线取值范围
例3、 已知三角形的两边上的高分别为4和6,求第三边上的高线的取值范围。
二、课前小测试:
1.如图(A),已知∠DAC=90,∠CBD=90,EF是△DEC的高,DA=CB,则全等的三角形有( )
A. 4对 B. 3对 C. 2对 D . 1对
2.已知如图(B),Rt△ABC中,∠ACB=90 ,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )
A.AE=BE B. CE=AB C.∠CEB=2∠A D.AC=AB
3. 下列说法一定正确的是( )
A.三角形两边之和小于第三边 B.有一个角是锐角的三角形是锐角三角形
C.两边和一角对应相等的两个三角形全等 D.两角及一边对应相等的两个三角形全等
4. 下列对三角形中线说法不正确的是( )
A. 三角形的一条中线将这个三角形的一个角平分成相等的两个角.
B三角形的一条中线将这个三角形平分成面积相等的两个三角形.
C. 三角形的中线是连接一个顶点和它对边中点的线段.
D. 三角形的中线是线段,并交于一点.
5. 锐角三角形中任意两角之和一定大于( )
A.120 B.110 C.100 D.90
三、课后练习
1 、如图,已知△ABC中,AD是△ABC的中线,AB=8,AC=6,求AD的取值范围.
2、 如图,已知△ABC中,AB=AC,D在AB上,E是AC延长线上一点,且BD=CE,DE与BC交于点F. 求证:DF=EF.
3、 如图,已知RT△ACB中,∠C=90°,AC=BC,AD=AC,DE⊥AB,垂足为D,交BC于E.
求证:BD=DE=CE.
4 、如图,已知△ABC中,∠B=2∠C,AD平分∠BAC交BC于D.
求证:AC=AB+BD.
5、如图,已知CE、CB分别是△ABC和△ADC的中线,且AB=AC.求证:CD=2CE.
6、 如图,已知∠BAC=∠DAE,∠ABD=∠ACE,BD=CE.求证:AB=AC,AD=AE.
7、 如图,在△ABC中,BD=DC,ED⊥DF.求证:BE+CF>EF.
图(B)
图(A)
同课章节目录
