全等三角形证明辅助线作法--倍长中线问题
文档属性
| 名称 | 全等三角形证明辅助线作法--倍长中线问题 |
|
|
| 格式 | zip | ||
| 文件大小 | 33.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-05-31 00:00:00 | ||
图片预览

文档简介
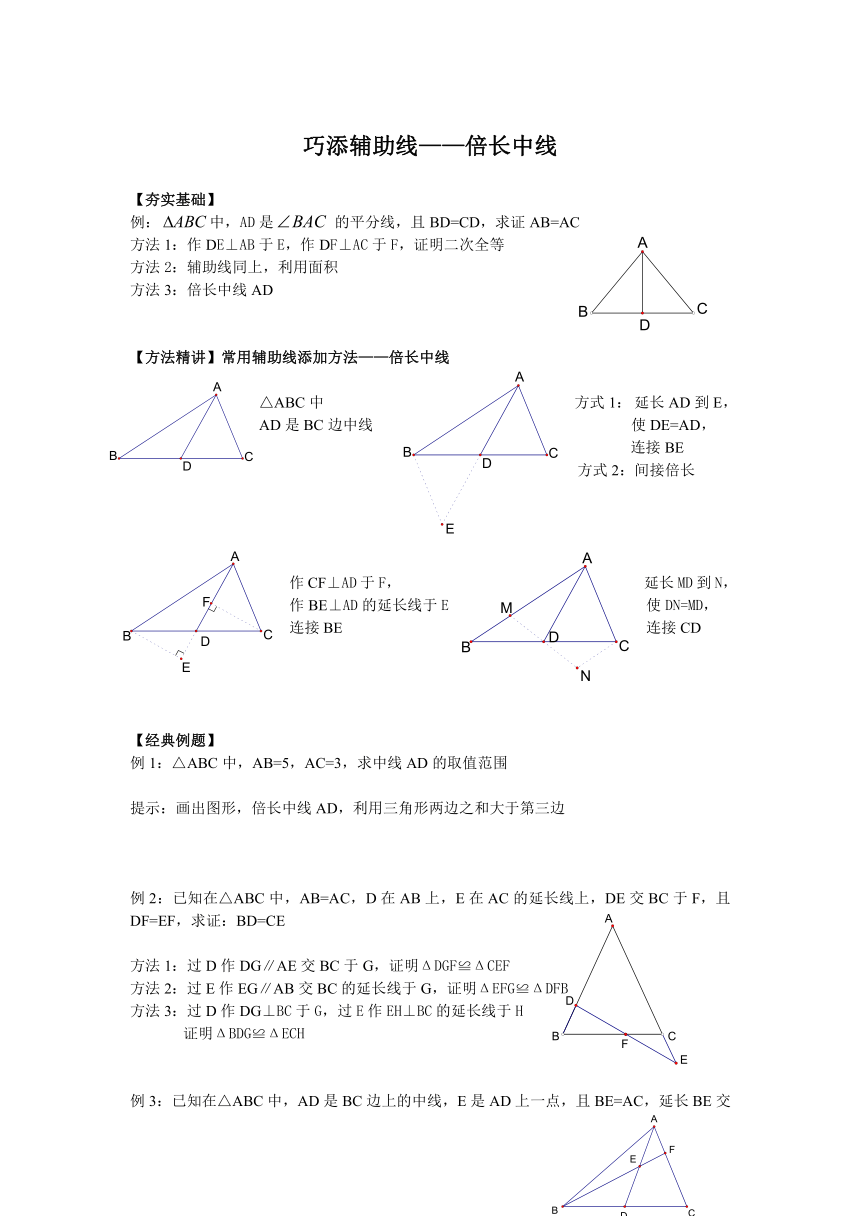
巧添辅助线——倍长中线
【夯实基础】
例:中,AD是的平分线,且BD=CD,求证AB=AC
方法1:作DE⊥AB于E,作DF⊥AC于F,证明二次全等
方法2:辅助线同上,利用面积
方法3:倍长中线AD
【方法精讲】常用辅助线添加方法——倍长中线
△ABC中 方式1: 延长AD到E,
AD是BC边中线 使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F, 延长MD到N,
作BE⊥AD的延长线于E 使DN=MD,
连接BE 连接CD
【经典例题】
例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
提示:画出图形,倍长中线AD,利用三角形两边之和大于第三边
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
方法1:过D作DG∥AE交BC于G,证明ΔDGF≌ΔCEF
方法2:过E作EG∥AB交BC的延长线于G,证明ΔEFG≌ΔDFB
方法3:过D作DG⊥BC于G,过E作EH⊥BC的延长线于H
证明ΔBDG≌ΔECH
例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
提示:倍长AD至G,连接BG,证明ΔBDG≌ΔCDA
三角形BEG是等腰三角形
例4:已知:如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC.
求证:AE平分
提示:
方法1:倍长AE至G,连结DG
方法2:倍长FE至H,连结CH
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
提示:倍长AE至F,连结DF
证明ΔABE≌ΔFDE(SAS)
进而证明ΔADF≌ΔADC(SAS)
【融会贯通】
1、在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的数量关系,并证明你的结论
提示:延长AE、DF交于G
证明AB=GC、AF=GF
所以AB=AF+FC
2、如图,AD为的中线,DE平分交AB于E,DF平分交AC于F. 求证:
提示:
方法1:在DA上截取DG=BD,连结EG、FG
证明ΔBDE≌ΔGDE ΔDCF≌ΔDGF
所以BE=EG、CF=FG
利用三角形两边之和大于第三边
方法2:倍长ED至H,连结CH、FH
证明FH=EF、CH=BE
利用三角形两边之和大于第三边
3、已知:如图,ABC中,C=90,CMAB于M,AT平分BAC交CM于D,交BC于T,过D作DE//AB交BC于E,求证:CT=BE.
提示:过T作TN⊥AB于N
证明ΔBTN≌ΔECD
【夯实基础】
例:中,AD是的平分线,且BD=CD,求证AB=AC
方法1:作DE⊥AB于E,作DF⊥AC于F,证明二次全等
方法2:辅助线同上,利用面积
方法3:倍长中线AD
【方法精讲】常用辅助线添加方法——倍长中线
△ABC中 方式1: 延长AD到E,
AD是BC边中线 使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F, 延长MD到N,
作BE⊥AD的延长线于E 使DN=MD,
连接BE 连接CD
【经典例题】
例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
提示:画出图形,倍长中线AD,利用三角形两边之和大于第三边
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
方法1:过D作DG∥AE交BC于G,证明ΔDGF≌ΔCEF
方法2:过E作EG∥AB交BC的延长线于G,证明ΔEFG≌ΔDFB
方法3:过D作DG⊥BC于G,过E作EH⊥BC的延长线于H
证明ΔBDG≌ΔECH
例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
提示:倍长AD至G,连接BG,证明ΔBDG≌ΔCDA
三角形BEG是等腰三角形
例4:已知:如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC.
求证:AE平分
提示:
方法1:倍长AE至G,连结DG
方法2:倍长FE至H,连结CH
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
提示:倍长AE至F,连结DF
证明ΔABE≌ΔFDE(SAS)
进而证明ΔADF≌ΔADC(SAS)
【融会贯通】
1、在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的数量关系,并证明你的结论
提示:延长AE、DF交于G
证明AB=GC、AF=GF
所以AB=AF+FC
2、如图,AD为的中线,DE平分交AB于E,DF平分交AC于F. 求证:
提示:
方法1:在DA上截取DG=BD,连结EG、FG
证明ΔBDE≌ΔGDE ΔDCF≌ΔDGF
所以BE=EG、CF=FG
利用三角形两边之和大于第三边
方法2:倍长ED至H,连结CH、FH
证明FH=EF、CH=BE
利用三角形两边之和大于第三边
3、已知:如图,ABC中,C=90,CMAB于M,AT平分BAC交CM于D,交BC于T,过D作DE//AB交BC于E,求证:CT=BE.
提示:过T作TN⊥AB于N
证明ΔBTN≌ΔECD
同课章节目录
