人教版数学九年级下册 27.2.1 相似三角形的判定(复习)学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册 27.2.1 相似三角形的判定(复习)学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 146.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-24 18:26:35 | ||
图片预览

文档简介
27.2.1相似三角形的判定(复习)
导学目标知识点:掌握两个三角形相似的判定方法;会用其解决问题.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
两个三角形相似的判断方法:
1.定义:两个三角形的 , ,这个两个三角形相似.
2.预备定理: 于三角形一边的直线和其他两边(或 )相交,所构成的三角形与原三角形 .
3.判定定理1: .→(SSS)
4.判定定理2: .→(SAS)
5.判定定理3: .→(ASA或AAS)
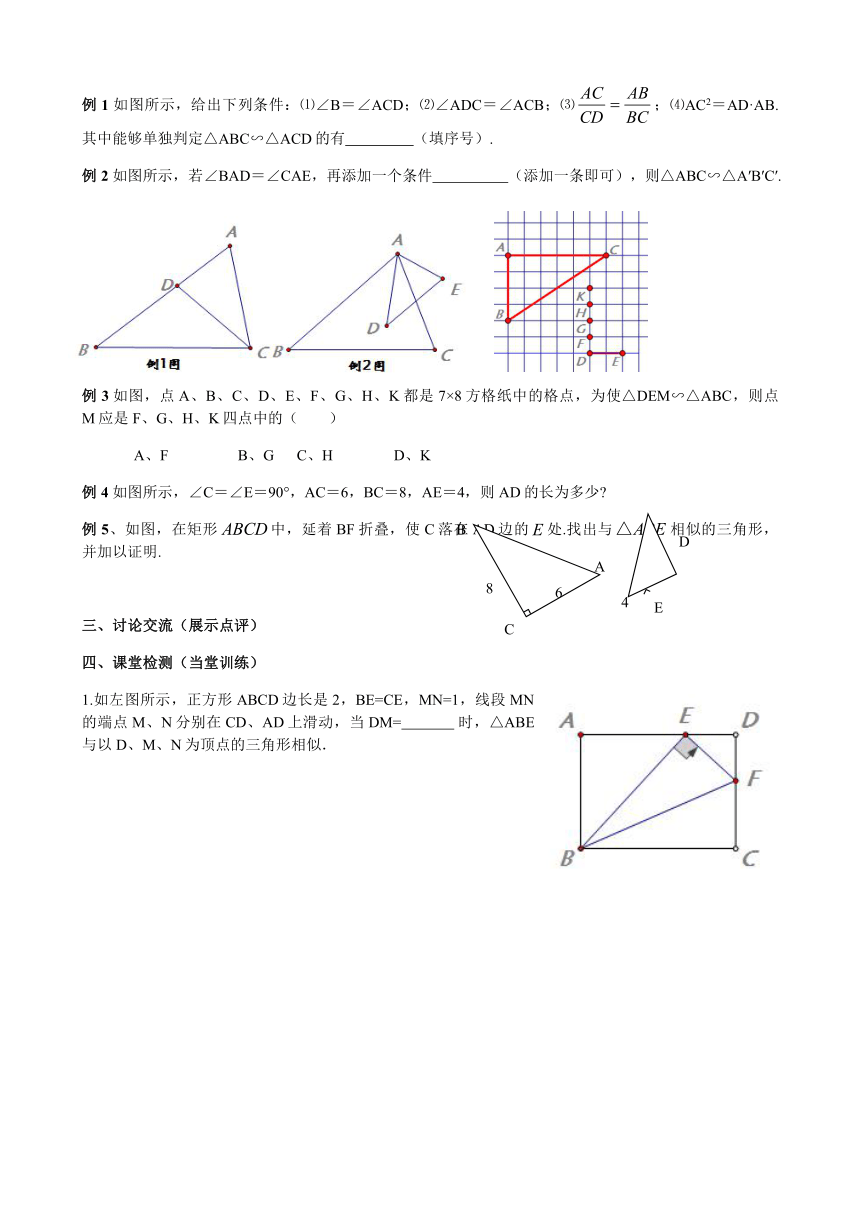
6.相似三角形的判定方法
二、合作探究(课堂导学)
例1 如图所示,给出下列条件:⑴∠B=∠ACD;⑵∠ADC=∠ACB;⑶;⑷AC2=AD·AB.其中能够单独判定△ABC∽△ACD的有 (填序号).
例2 如图所示,若∠BAD=∠CAE,再添加一个条件 (添加一条即可),则△ABC∽△A′B′C′.
例3如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F、G、H、K四点中的( )
A、F B、G C、H D、K
例4 如图所示,∠C=∠E=90°,AC=6,BC=8,AE=4,则AD的长为多少
例5、如图,在矩形中,延着BF折叠,使C落在AD边的处.找出与相似的三角形,并加以证明.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
1.如左图所示,正方形ABCD边长是2,BE=CE,MN=1,线段MN的端点M、N分别在CD、AD上滑动,当DM= 时,△ABE与以D、M、N为顶点的三角形相似.
2.如右图,在△ABC中,AD是BC边上的中线,点N在AB边上,且AN:AB=1:5,CN交AD与M点,则AM:MD的比为( )
A.1:2 B.1:3 C.2:3 D.1:1
3.如图所示,已知E是矩形ABCD的边CD上一点,BF⊥AE于F.试证明:AB·AD=AE·BF
四、拓展延伸(课外练习):
1.在△ABC与△A′B′C′中,有下列条件:⑴;⑵;⑶∠A=∠A′;⑷∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A、1组 B、2组 C、3组 D、4组
2.如图上图所示,已知点E在AC上,若点D在AB上,则满足
条件(只填一个条件),使△ADE与原△ABC相似,并写出证明过程.
3.在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标.
4.如图所示,在正方形ABCD中,有一块直角三板按图摆放.
(1)写出图中的相似的三角形;
(2)从上面任选一组进行证明
B
C
E
D
A
8
6
4
导学目标知识点:掌握两个三角形相似的判定方法;会用其解决问题.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
两个三角形相似的判断方法:
1.定义:两个三角形的 , ,这个两个三角形相似.
2.预备定理: 于三角形一边的直线和其他两边(或 )相交,所构成的三角形与原三角形 .
3.判定定理1: .→(SSS)
4.判定定理2: .→(SAS)
5.判定定理3: .→(ASA或AAS)
6.相似三角形的判定方法
二、合作探究(课堂导学)
例1 如图所示,给出下列条件:⑴∠B=∠ACD;⑵∠ADC=∠ACB;⑶;⑷AC2=AD·AB.其中能够单独判定△ABC∽△ACD的有 (填序号).
例2 如图所示,若∠BAD=∠CAE,再添加一个条件 (添加一条即可),则△ABC∽△A′B′C′.
例3如图,点A、B、C、D、E、F、G、H、K都是7×8方格纸中的格点,为使△DEM∽△ABC,则点M应是F、G、H、K四点中的( )
A、F B、G C、H D、K
例4 如图所示,∠C=∠E=90°,AC=6,BC=8,AE=4,则AD的长为多少
例5、如图,在矩形中,延着BF折叠,使C落在AD边的处.找出与相似的三角形,并加以证明.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
1.如左图所示,正方形ABCD边长是2,BE=CE,MN=1,线段MN的端点M、N分别在CD、AD上滑动,当DM= 时,△ABE与以D、M、N为顶点的三角形相似.
2.如右图,在△ABC中,AD是BC边上的中线,点N在AB边上,且AN:AB=1:5,CN交AD与M点,则AM:MD的比为( )
A.1:2 B.1:3 C.2:3 D.1:1
3.如图所示,已知E是矩形ABCD的边CD上一点,BF⊥AE于F.试证明:AB·AD=AE·BF
四、拓展延伸(课外练习):
1.在△ABC与△A′B′C′中,有下列条件:⑴;⑵;⑶∠A=∠A′;⑷∠C=∠C′.如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A、1组 B、2组 C、3组 D、4组
2.如图上图所示,已知点E在AC上,若点D在AB上,则满足
条件(只填一个条件),使△ADE与原△ABC相似,并写出证明过程.
3.在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标.
4.如图所示,在正方形ABCD中,有一块直角三板按图摆放.
(1)写出图中的相似的三角形;
(2)从上面任选一组进行证明
B
C
E
D
A
8
6
4
