湘教版九年级数学下册《函数的应用——建模》教学设计
文档属性
| 名称 | 湘教版九年级数学下册《函数的应用——建模》教学设计 | 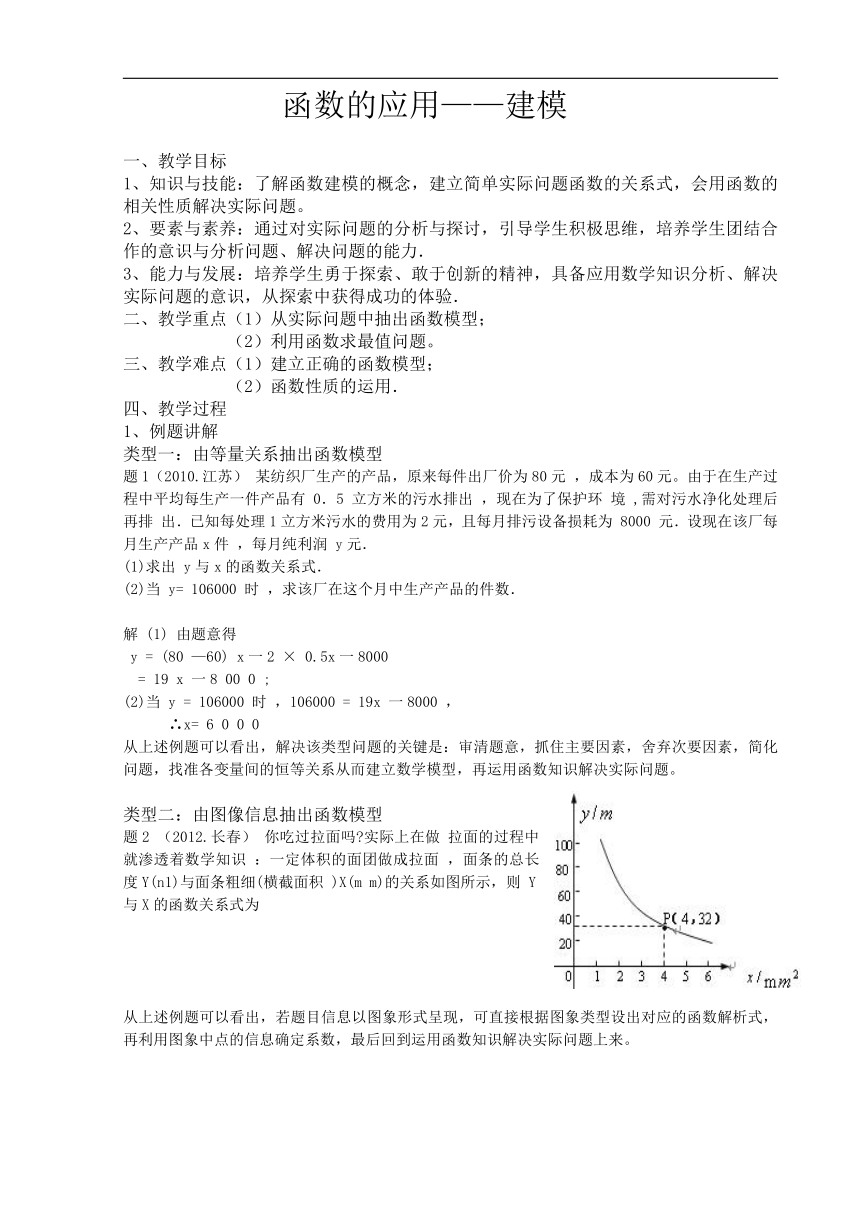 | |
| 格式 | docx | ||
| 文件大小 | 43.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 08:19:29 | ||
图片预览

文档简介
函数的应用——建模
一、教学目标
1、知识与技能:了解函数建模的概念,建立简单实际问题函数的关系式,会用函数的相关性质解决实际问题。
2、要素与素养:通过对实际问题的分析与探讨,引导学生积极思维,培养学生团结合作的意识与分析问题、解决问题的能力.
3、能力与发展:培养学生勇于探索、敢于创新的精神,具备应用数学知识分析、解决实际问题的意识,从探索中获得成功的体验.
二、教学重点(1)从实际问题中抽出函数模型;
(2)利用函数求最值问题。
三、教学难点(1)建立正确的函数模型;
(2)函数性质的运用.
四、教学过程
1、例题讲解
类型一:由等量关系抽出函数模型
题1(2010.江苏) 某纺织厂生产的产品,原来每件出厂价为80元 ,成本为60元。由于在生产过程中平均每生产一件产品有 0.5 立方米的污水排出 ,现在为了保护环 境 ,需对污水净化处理后再排 出.已知每处理1立方米污水的费用为2元,且每月排污设备损耗为 8000 元.设现在该厂每月生产产品x件 ,每月纯利润 y元.
(1)求出 y与x的函数关系式.
(2)当 y= 106000 时 ,求该厂在这个月中生产产品的件数.
解 (1) 由题意得
y = (80 —60) x一2 × 0.5x一8000
= 19 x 一8 00 0 ;
(2)当 y = 106000 时 ,106000 = 19x 一8000 ,
∴x= 6 0 0 0
从上述例题可以看出,解决该类型问题的关键是:审清题意,抓住主要因素,舍弃次要因素,简化问题,找准各变量间的恒等关系从而建立数学模型,再运用函数知识解决实际问题。
类型二:由图像信息抽出函数模型
题2 (2012.长春) 你吃过拉面吗 实际上在做 拉面的过程中就渗透着数学知识 :一定体积的面团做成拉面 ,面条的总长度Y(n1)与面条粗细(横截面积 )X(m m)的关系如图所示,则 Y与X的函数关系式为
从上述例题可以看出,若题目信息以图象形式呈现,可直接根据图象类型设出对应的函数解析式,再利用图象中点的信息确定系数,最后回到运用函数知识解决实际问题上来。
类型三:由几何关系抽出函数模型
题3 (2009.南京)在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=120°,设AE=x,DF=y.
(1)求y与x的函数表达式;
(2)当x为何值时,y有最大值,最大值是多少?
类型四:由表格信息抽出函数模型
年 度 2005 2006 2007 2008
投入技改资金(万元) 2.5 3 4 4.5
产品成本(元/件) 7.2 6 4.5 4
题4(2012.福建改)某厂从2005年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如上表,认真分析表中数据,投入技改资金(万元)与产品成本(元/件)存在某种变化规律,按照这种变化规律,若2009年投入技改资金5万元,预计生产成本每件比2008年降低多少元?
题5(2015.广东改)某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
时间(第x天) 1 3 6 10 ……
日销售量(m件) 198 194 188 180 …….
产品50天内日销售量(m件)与时间(第x天)满足下表关系,部分数据如下:
该产品50天内每天的销售价格为(x+60)
(1)求m关于x的函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在50天内该产品哪天的销售利润最大?最大利润是多少?
2、知识小结:
函数建模法解应用题:
建模(关键:理解题,自变量取值范围)
判模(关键:判断是哪种已学函数模型)
用模(关键:函数模型知识的灵活运用)
3、作业布置。
一、教学目标
1、知识与技能:了解函数建模的概念,建立简单实际问题函数的关系式,会用函数的相关性质解决实际问题。
2、要素与素养:通过对实际问题的分析与探讨,引导学生积极思维,培养学生团结合作的意识与分析问题、解决问题的能力.
3、能力与发展:培养学生勇于探索、敢于创新的精神,具备应用数学知识分析、解决实际问题的意识,从探索中获得成功的体验.
二、教学重点(1)从实际问题中抽出函数模型;
(2)利用函数求最值问题。
三、教学难点(1)建立正确的函数模型;
(2)函数性质的运用.
四、教学过程
1、例题讲解
类型一:由等量关系抽出函数模型
题1(2010.江苏) 某纺织厂生产的产品,原来每件出厂价为80元 ,成本为60元。由于在生产过程中平均每生产一件产品有 0.5 立方米的污水排出 ,现在为了保护环 境 ,需对污水净化处理后再排 出.已知每处理1立方米污水的费用为2元,且每月排污设备损耗为 8000 元.设现在该厂每月生产产品x件 ,每月纯利润 y元.
(1)求出 y与x的函数关系式.
(2)当 y= 106000 时 ,求该厂在这个月中生产产品的件数.
解 (1) 由题意得
y = (80 —60) x一2 × 0.5x一8000
= 19 x 一8 00 0 ;
(2)当 y = 106000 时 ,106000 = 19x 一8000 ,
∴x= 6 0 0 0
从上述例题可以看出,解决该类型问题的关键是:审清题意,抓住主要因素,舍弃次要因素,简化问题,找准各变量间的恒等关系从而建立数学模型,再运用函数知识解决实际问题。
类型二:由图像信息抽出函数模型
题2 (2012.长春) 你吃过拉面吗 实际上在做 拉面的过程中就渗透着数学知识 :一定体积的面团做成拉面 ,面条的总长度Y(n1)与面条粗细(横截面积 )X(m m)的关系如图所示,则 Y与X的函数关系式为
从上述例题可以看出,若题目信息以图象形式呈现,可直接根据图象类型设出对应的函数解析式,再利用图象中点的信息确定系数,最后回到运用函数知识解决实际问题上来。
类型三:由几何关系抽出函数模型
题3 (2009.南京)在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=120°,设AE=x,DF=y.
(1)求y与x的函数表达式;
(2)当x为何值时,y有最大值,最大值是多少?
类型四:由表格信息抽出函数模型
年 度 2005 2006 2007 2008
投入技改资金(万元) 2.5 3 4 4.5
产品成本(元/件) 7.2 6 4.5 4
题4(2012.福建改)某厂从2005年起开始投入技术改进资金,经技术改进后,其产品的生产成本不断降低,具体数据如上表,认真分析表中数据,投入技改资金(万元)与产品成本(元/件)存在某种变化规律,按照这种变化规律,若2009年投入技改资金5万元,预计生产成本每件比2008年降低多少元?
题5(2015.广东改)某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
时间(第x天) 1 3 6 10 ……
日销售量(m件) 198 194 188 180 …….
产品50天内日销售量(m件)与时间(第x天)满足下表关系,部分数据如下:
该产品50天内每天的销售价格为(x+60)
(1)求m关于x的函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在50天内该产品哪天的销售利润最大?最大利润是多少?
2、知识小结:
函数建模法解应用题:
建模(关键:理解题,自变量取值范围)
判模(关键:判断是哪种已学函数模型)
用模(关键:函数模型知识的灵活运用)
3、作业布置。
