第11章 解三角形 章末复习提升课(共48张PPT)
文档属性
| 名称 | 第11章 解三角形 章末复习提升课(共48张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 18:46:19 | ||
图片预览










文档简介
(共48张PPT)
第11章 解三角形
章末复习提升课
01
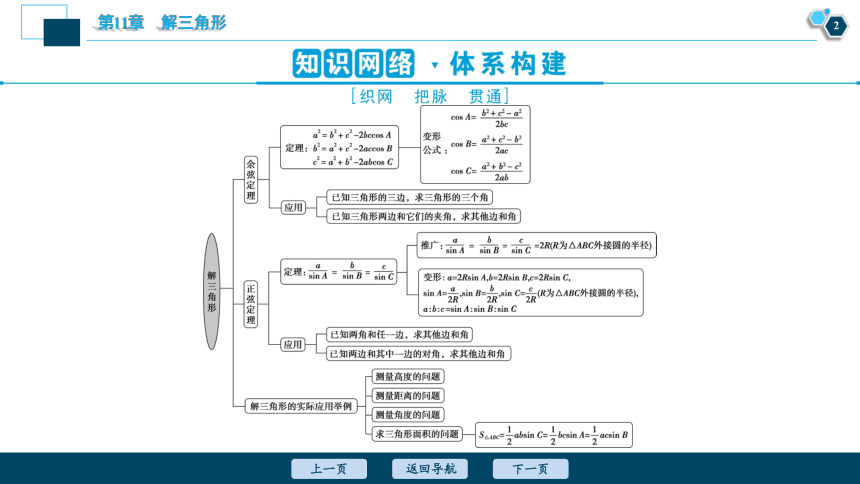
知识网络 体系构建
02
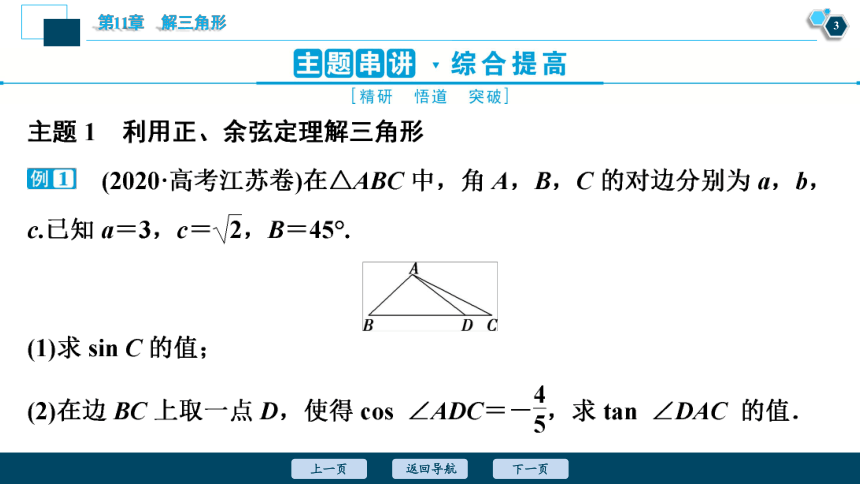
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
解三角形的一般方法
(1)已知两角和一边,如已知A,B和c,由A+B+C=π求C,由正弦定理求a,b.
(2)已知两边和这两边的夹角,如已知a,b和C,应先用余弦定理求c,再应用正弦定理先求较短边所对的角,然后利用A+B+C=π,求另一角.
(3)已知两边和其中一边的对角,如已知a,b和A,应先用正弦定理求B,由A+B+C=π求C,再由正弦定理或余弦定理求c,要注意解可能有多种情况.
(4)已知三边a,b,c,可应用余弦定理求A,B,C.
√
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则该三角形的形状是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
正、余弦定理在实际应用中应注意的问题
(1)分析题意,弄清已知元素和未知元素,根据题意画出示意图.
(2)明确题目中的一些名词、术语的意义,如仰角、俯角、方向角、方位角等.
(3)将实际问题中的数量关系归结为数学问题,利用学过的几何知识,作出辅助线,将已知与未知元素归结到同一个三角形中,然后解此三角形.
(4)在选择关系时,一是力求简便,二是要尽可能使用题目中的原有数据,尽量减少计算中误差的积累.
(5)按照题目中已有的精确度计算,并根据题目要求的精确度确定答案并注明单位.
正、余弦定理与三角函数综合应用的求解策略
(1)首先要熟练使用正、余弦定理,其次要根据条件,合理选用三角函数公式,达到简化问题的目的.
(2)利用正、余弦定理解三角形问题时,常与平面向量等知识结合给出问题的条件,这些知识的加入,一般只起“点缀”作用,难度较小,易于化简.
√
√
3.在△ABC中,已知sin2A=sin2B+sin2C,且sinA=2sin B cos C,则△ABC的形状是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
本部分内容讲解结束
按ESC键退出全屏播放
第11章 解三角形
章末复习提升课
01
知识网络 体系构建
02
主题串讲 综合提高
03
热考强化 素养提升
04
章末演练 轻松闯关
解三角形的一般方法
(1)已知两角和一边,如已知A,B和c,由A+B+C=π求C,由正弦定理求a,b.
(2)已知两边和这两边的夹角,如已知a,b和C,应先用余弦定理求c,再应用正弦定理先求较短边所对的角,然后利用A+B+C=π,求另一角.
(3)已知两边和其中一边的对角,如已知a,b和A,应先用正弦定理求B,由A+B+C=π求C,再由正弦定理或余弦定理求c,要注意解可能有多种情况.
(4)已知三边a,b,c,可应用余弦定理求A,B,C.
√
在△ABC中,若lg sin A-lg cos B-lg sin C=lg 2,则该三角形的形状是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
正、余弦定理在实际应用中应注意的问题
(1)分析题意,弄清已知元素和未知元素,根据题意画出示意图.
(2)明确题目中的一些名词、术语的意义,如仰角、俯角、方向角、方位角等.
(3)将实际问题中的数量关系归结为数学问题,利用学过的几何知识,作出辅助线,将已知与未知元素归结到同一个三角形中,然后解此三角形.
(4)在选择关系时,一是力求简便,二是要尽可能使用题目中的原有数据,尽量减少计算中误差的积累.
(5)按照题目中已有的精确度计算,并根据题目要求的精确度确定答案并注明单位.
正、余弦定理与三角函数综合应用的求解策略
(1)首先要熟练使用正、余弦定理,其次要根据条件,合理选用三角函数公式,达到简化问题的目的.
(2)利用正、余弦定理解三角形问题时,常与平面向量等知识结合给出问题的条件,这些知识的加入,一般只起“点缀”作用,难度较小,易于化简.
√
√
3.在△ABC中,已知sin2A=sin2B+sin2C,且sinA=2sin B cos C,则△ABC的形状是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
√
本部分内容讲解结束
按ESC键退出全屏播放
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
