人教版数学九年级下册 27.2.1 相似三角形的判定(4)学案(无答案)
文档属性
| 名称 | 人教版数学九年级下册 27.2.1 相似三角形的判定(4)学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 109.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 17:55:44 | ||
图片预览

文档简介
27.2.1 相似三角形的判定 4
导学目标知识点:掌握“两角对应相等,两个三角形相似”的判定方法.
能够运用三角形相似的条件解决简单的问题.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
1、我们已学习过哪些判定三角形相似的方法?
2、如图,△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?说说你的理由.
二、合作探究(课堂导学)
实验探究:如第2题图,△ABC中,点D在AB上,如果∠ACD=∠B,那么△ACD与△ABC相似吗?
归纳 三角形相似的判定方法3
例1.如图,与都是的内接三角形,和相交与点,找出图中的一对相似三角形,并说明理由.
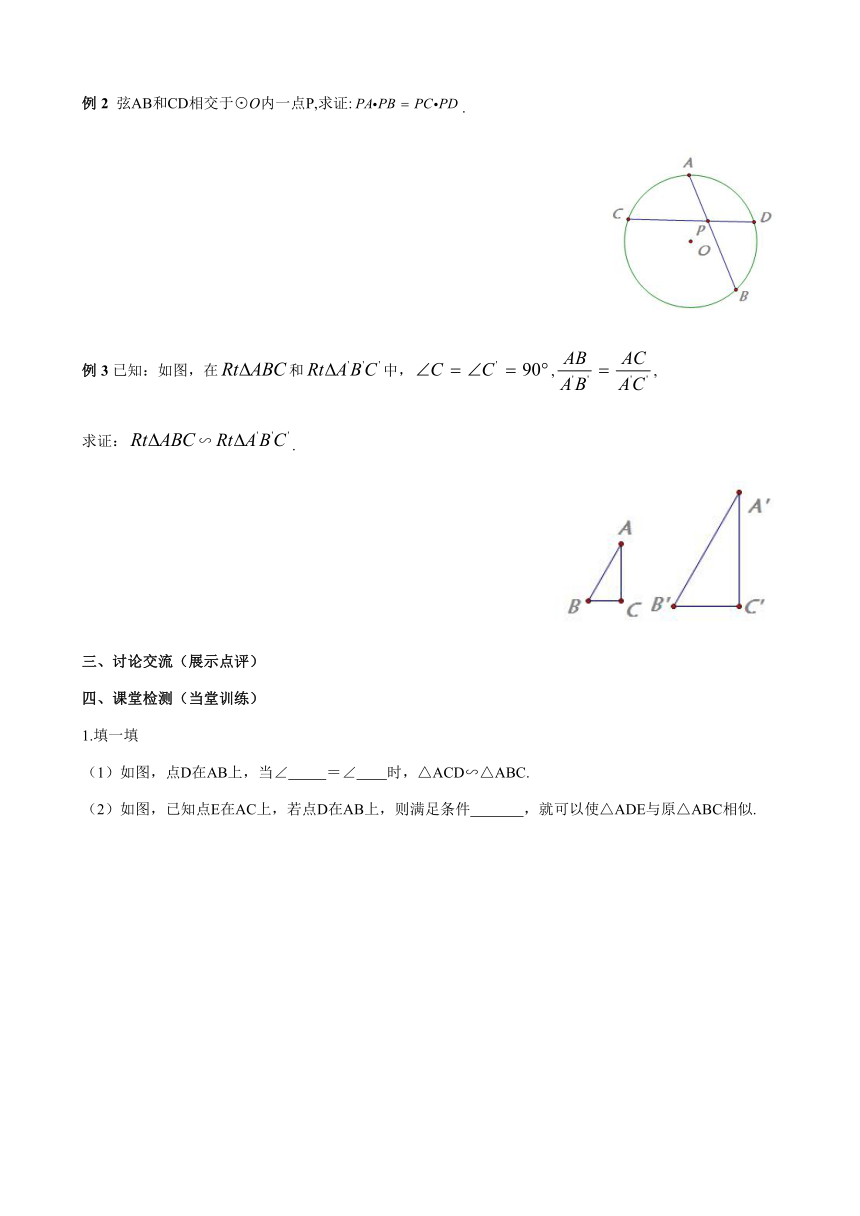
例 2 弦AB和CD相交于⊙O内一点P,求证:.
例 3 已知:如图,在和中,,,
求证:∽.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
1.填一填
(1)如图,点D在AB上,当∠ =∠ 时,△ACD∽△ABC.
(2)如图,已知点E在AC上,若点D在AB上,则满足条件 ,就可以使△ADE与原△ABC相似.
2.下列说法是否正确,并说明理由.
(1)有一个锐角相等的两直角三角形是相似三角形;
(2)有一个角相等的两等腰三角形是相似三角形;
(3)底角相等的两个等腰三角形相似.
3.如图,在中,CD是斜边上的高,和都与相似吗?证明你的结论.
4.如图,△ABC中, DE∥BC,EF∥AB,试说明△ADE ∽△EFC.
拓展延伸(课外练习):
1.(1)左图中DE∥FG∥BC,找出图中所有的相似三角形.
(2)右图中AB∥CD∥EF,找出图中所有的相似三角形.
2.在和中,如果,,,,那么这两个三角形是否相似?为什么?
3.如图,△ABC 的高AD、BE交于点F.求证:.
4.已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
导学目标知识点:掌握“两角对应相等,两个三角形相似”的判定方法.
能够运用三角形相似的条件解决简单的问题.
课 时:1课时
导学方法:整理、分析、归纳法
导学过程:
一、自主探究(课前导学)
1、我们已学习过哪些判定三角形相似的方法?
2、如图,△ABC中,点D在AB上,如果AC2=AD AB,那么△ACD与△ABC相似吗?说说你的理由.
二、合作探究(课堂导学)
实验探究:如第2题图,△ABC中,点D在AB上,如果∠ACD=∠B,那么△ACD与△ABC相似吗?
归纳 三角形相似的判定方法3
例1.如图,与都是的内接三角形,和相交与点,找出图中的一对相似三角形,并说明理由.
例 2 弦AB和CD相交于⊙O内一点P,求证:.
例 3 已知:如图,在和中,,,
求证:∽.
三、讨论交流(展示点评)
四、课堂检测(当堂训练)
1.填一填
(1)如图,点D在AB上,当∠ =∠ 时,△ACD∽△ABC.
(2)如图,已知点E在AC上,若点D在AB上,则满足条件 ,就可以使△ADE与原△ABC相似.
2.下列说法是否正确,并说明理由.
(1)有一个锐角相等的两直角三角形是相似三角形;
(2)有一个角相等的两等腰三角形是相似三角形;
(3)底角相等的两个等腰三角形相似.
3.如图,在中,CD是斜边上的高,和都与相似吗?证明你的结论.
4.如图,△ABC中, DE∥BC,EF∥AB,试说明△ADE ∽△EFC.
拓展延伸(课外练习):
1.(1)左图中DE∥FG∥BC,找出图中所有的相似三角形.
(2)右图中AB∥CD∥EF,找出图中所有的相似三角形.
2.在和中,如果,,,,那么这两个三角形是否相似?为什么?
3.如图,△ABC 的高AD、BE交于点F.求证:.
4.已知:如图,BE是△ABC的外接圆O的直径,CD是△ABC的高.
(1)求证:;
(2)若CD=6,AD=3,BD=8,求⊙O的直径BE的长.
