2021-2022学年鲁教版(五四制)七年级数学下册 10.5 角平分线 教案(表格式)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册 10.5 角平分线 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 67.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-26 00:00:00 | ||
图片预览

文档简介
课题 5 角平分线 课时 1课时 上课时间
教学目标 1.经历角平分线的性质的证明过程,掌握角平分线的性质定理及逆定理. 2.能运用角平分线的性质定理及逆定理解决有关问题.
教学 重难点 重点:线段的垂直平分线的性质、判定定理的证明. 难点:尺规作已知线段的垂直平分线.
教学活动设计 二次设计
课堂导入 画出一个角,并画出该角的角平分线
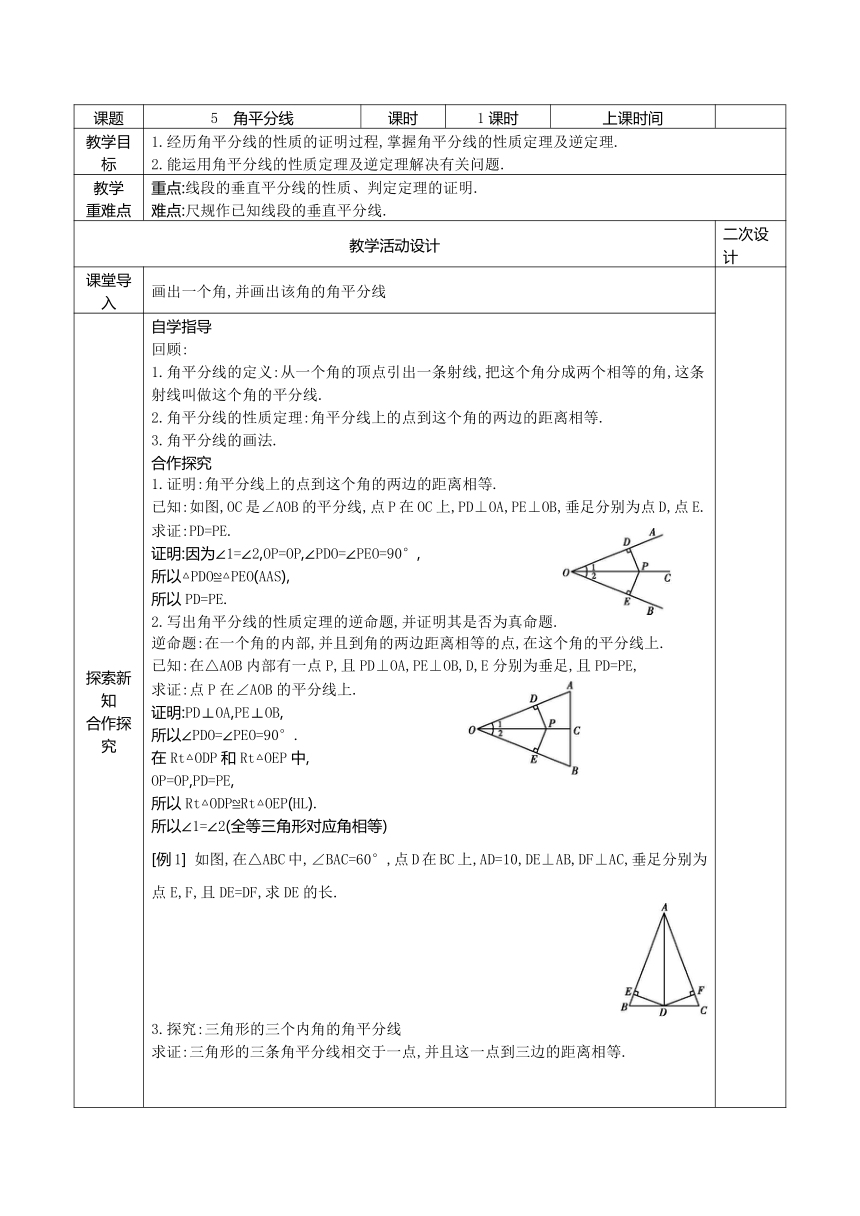
探索新知 合作探究 自学指导 回顾: 1.角平分线的定义:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线. 2.角平分线的性质定理:角平分线上的点到这个角的两边的距离相等. 3.角平分线的画法. 合作探究 1.证明:角平分线上的点到这个角的两边的距离相等. 已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,点E. 求证:PD=PE. 证明:因为∠1=∠2,OP=OP,∠PDO=∠PEO=90°, 所以△PDO≌△PEO(AAS), 所以PD=PE. 2.写出角平分线的性质定理的逆命题,并证明其是否为真命题. 逆命题:在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上. 已知:在△AOB内部有一点P,且PD⊥OA,PE⊥OB,D,E分别为垂足,且PD=PE, 求证:点P在∠AOB的平分线上. 证明:PD⊥OA,PE⊥OB, 所以∠PDO=∠PEO=90°. 在Rt△ODP和Rt△OEP中, OP=OP,PD=PE, 所以Rt△ODP≌Rt△OEP(HL). 所以∠1=∠2(全等三角形对应角相等) [例1] 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长. 3.探究:三角形的三个内角的角平分线 求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.
续表
探索新知 合作探究 已知:如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别是D,E,F. 求证:点P在∠A的平分线上,且PD=PE=PF. 证明:因为BM是△ABC的角平分线,点P在BM上, 所以PD= . 同理,PE= . 所以PD= = . 即点P在∠A的平分线上,点P到三边AB,BC,CA的距离相等. [例2] 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E. (1)已知CD= cm,求AB的长; (2)求证:AB=AC+CD. 教师指导 1.角平分线上的点到这个角两边的距离相等. 2.在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上. 3.三角形三条角平分线相交于一点,并且这一点到三边的距离相等.
当堂训练 1.如图所示,在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB.垂足分别为点D,E,F,且AB=10,BC=8,则点O到三边AB,AC和BC的距离分别是( ) (A)2,2,2 (B)3,3,3 (C)4,4,4 (D)2,3,5 2.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,点B.下列结论中不一定成立的是( ) (A)PA=PB (B)PO平分∠APB (C)OA=OB (D)AB垂直平分OP 3.如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=5,BC=6,则AD= . 4.如图,在△ABC中,∠C=90°,D为BC上的一点,且DA=DB,DC=AC,则∠B= . 第1题图 第2题图 第3题图 第4题图
板书设计
角平分线 1.角平分线的性质定理 2.角平分线的判定定理 3.定理:三角形的三条角平分线交于一点,并且这一点到三边的距离相等
教学反思
本节课以学生的思维进程发展为主线,采用逐步渗透,螺旋式类比方法,在定理引入时,从动手作图,到证明,逐渐加深学生的认识,主要体现在从一开始一连串的知识性问题引入,到后来环节中多次提出思考性的问题,启发、引导学生做进一步的猜想、探究,这种循序渐进的思维进程有助于学生理解接受新知识.
教学目标 1.经历角平分线的性质的证明过程,掌握角平分线的性质定理及逆定理. 2.能运用角平分线的性质定理及逆定理解决有关问题.
教学 重难点 重点:线段的垂直平分线的性质、判定定理的证明. 难点:尺规作已知线段的垂直平分线.
教学活动设计 二次设计
课堂导入 画出一个角,并画出该角的角平分线
探索新知 合作探究 自学指导 回顾: 1.角平分线的定义:从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线. 2.角平分线的性质定理:角平分线上的点到这个角的两边的距离相等. 3.角平分线的画法. 合作探究 1.证明:角平分线上的点到这个角的两边的距离相等. 已知:如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,点E. 求证:PD=PE. 证明:因为∠1=∠2,OP=OP,∠PDO=∠PEO=90°, 所以△PDO≌△PEO(AAS), 所以PD=PE. 2.写出角平分线的性质定理的逆命题,并证明其是否为真命题. 逆命题:在一个角的内部,并且到角的两边距离相等的点,在这个角的平分线上. 已知:在△AOB内部有一点P,且PD⊥OA,PE⊥OB,D,E分别为垂足,且PD=PE, 求证:点P在∠AOB的平分线上. 证明:PD⊥OA,PE⊥OB, 所以∠PDO=∠PEO=90°. 在Rt△ODP和Rt△OEP中, OP=OP,PD=PE, 所以Rt△ODP≌Rt△OEP(HL). 所以∠1=∠2(全等三角形对应角相等) [例1] 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为点E,F,且DE=DF,求DE的长. 3.探究:三角形的三个内角的角平分线 求证:三角形的三条角平分线相交于一点,并且这一点到三边的距离相等.
续表
探索新知 合作探究 已知:如图,设△ABC的角平分线BM,CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别是D,E,F. 求证:点P在∠A的平分线上,且PD=PE=PF. 证明:因为BM是△ABC的角平分线,点P在BM上, 所以PD= . 同理,PE= . 所以PD= = . 即点P在∠A的平分线上,点P到三边AB,BC,CA的距离相等. [例2] 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E. (1)已知CD= cm,求AB的长; (2)求证:AB=AC+CD. 教师指导 1.角平分线上的点到这个角两边的距离相等. 2.在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上. 3.三角形三条角平分线相交于一点,并且这一点到三边的距离相等.
当堂训练 1.如图所示,在△ABC中,∠ACB=90°,点O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB.垂足分别为点D,E,F,且AB=10,BC=8,则点O到三边AB,AC和BC的距离分别是( ) (A)2,2,2 (B)3,3,3 (C)4,4,4 (D)2,3,5 2.如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为点A,点B.下列结论中不一定成立的是( ) (A)PA=PB (B)PO平分∠APB (C)OA=OB (D)AB垂直平分OP 3.如图,在△ABC中,AB=AC,∠BAC的平分线交BC边于点D,AB=5,BC=6,则AD= . 4.如图,在△ABC中,∠C=90°,D为BC上的一点,且DA=DB,DC=AC,则∠B= . 第1题图 第2题图 第3题图 第4题图
板书设计
角平分线 1.角平分线的性质定理 2.角平分线的判定定理 3.定理:三角形的三条角平分线交于一点,并且这一点到三边的距离相等
教学反思
本节课以学生的思维进程发展为主线,采用逐步渗透,螺旋式类比方法,在定理引入时,从动手作图,到证明,逐渐加深学生的认识,主要体现在从一开始一连串的知识性问题引入,到后来环节中多次提出思考性的问题,启发、引导学生做进一步的猜想、探究,这种循序渐进的思维进程有助于学生理解接受新知识.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
