29.1.2 正投影同步练习(含答案)
图片预览



文档简介
29.1 投 影
第2课时 正投影
一、选择题
1.若木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
2.球的正投影是( )
A.圆面 B.椭圆面 C.点 D.圆环
3.【中考·绥化】正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
4.下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
5.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( )
6.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD B.AB≤CD C.AB>CD D.AB≥CD
7.当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2 B.300 cm2 C.400 cm2 D.600 cm2
8.几何体在平面P的正投影,取决于( )
①几何体的形状;
②投影面与几何体的位置关系;
③投影面P的大小.
A.①② B.①③ C.②③ D.①②③
9.如图,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
10.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.矩形 C.梯形 D.圆柱
11.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( )
A.变小 B.变大 C.不发生变化 D.无法确定
12.当棱长为10 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.10 cm2 B.100 cm2 C.200 cm2 D.300 cm2
二、填空题
13.投影线 于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为 ;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为 ;
(3)当线段垂直于投影面时,它的正投影是 .当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 .
14.平行于投影面的平行四边形的面积 它的正投影的面积.(填“大于”“小于”或“等于”)
15.如图是一个三棱柱,投影线的方向如箭头所示,它的正投影是下图中的____.(填序号)
16.如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是_____________.
17.如图,正三棱柱的面EFDC∥平面R且AE=EF=AF=2,AB=6,正三棱柱在平面R的正投影是________,正投影的面积为_______.
18.小明喜欢玩魔方,已知他的魔方的棱长为5.5 cm,若魔方的一面平行于投影面,则这个面的正投影的面积为 cm2.
三、解答题
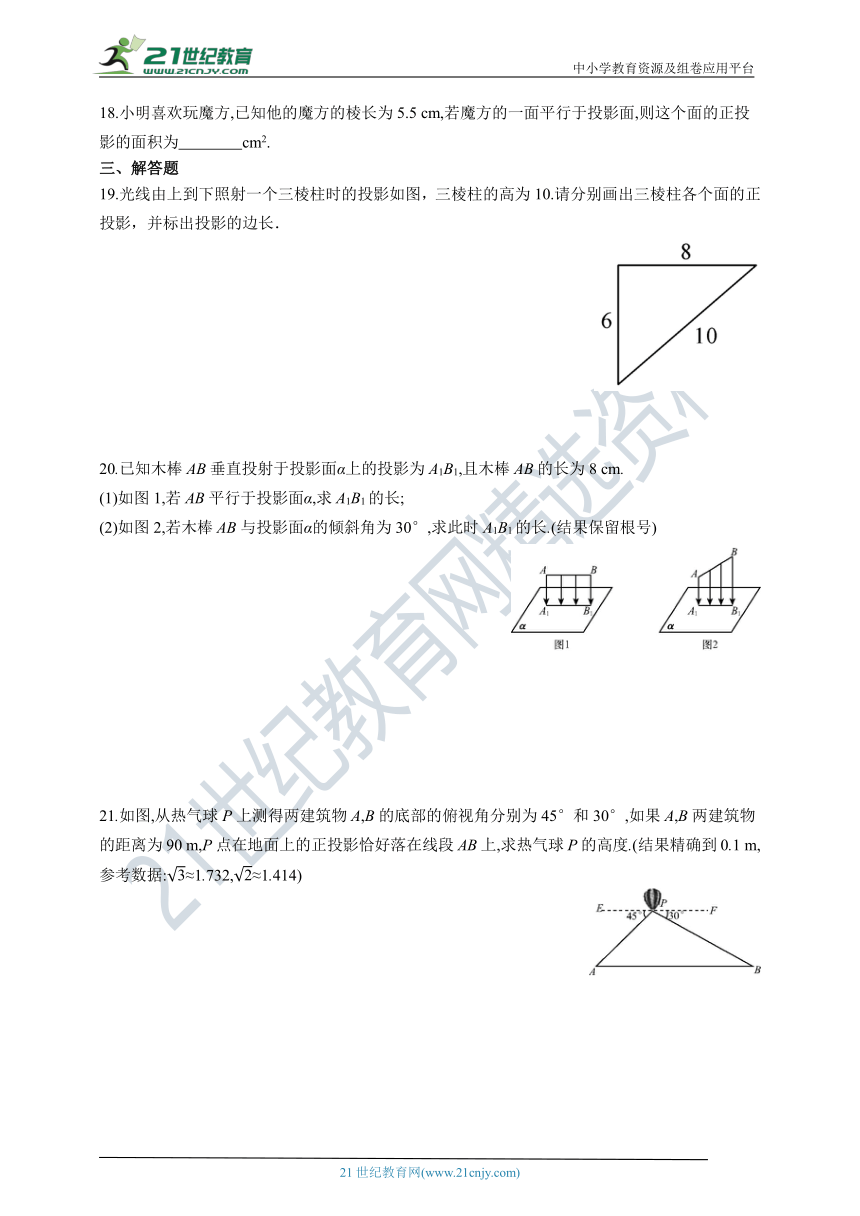
19.光线由上到下照射一个三棱柱时的投影如图,三棱柱的高为10.请分别画出三棱柱各个面的正投影,并标出投影的边长.
20.已知木棒AB垂直投射于投影面α上的投影为A1B1,且木棒AB的长为8 cm.
(1)如图1,若AB平行于投影面α,求A1B1的长;
(2)如图2,若木棒AB与投影面α的倾斜角为30°,求此时A1B1的长.(结果保留根号)
21.如图,从热气球P上测得两建筑物A,B的底部的俯视角分别为45°和30°,如果A,B两建筑物的距离为90 m,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果精确到0.1 m,参考数据:≈1.732,≈1.414)
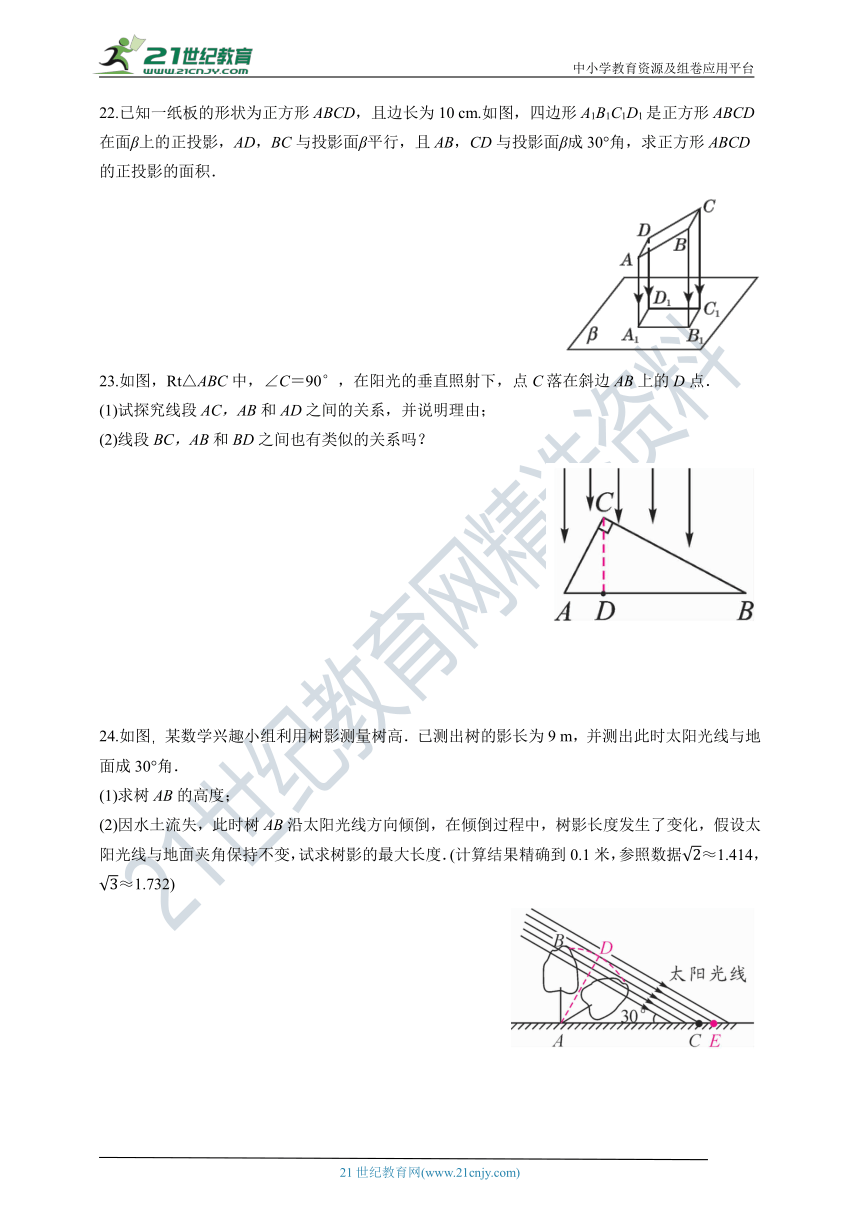
22.已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD在面β上的正投影,AD,BC与投影面β平行,且AB,CD与投影面β成30°角,求正方形ABCD的正投影的面积.
23.如图,Rt△ABC中,∠C=90°,在阳光的垂直照射下,点C落在斜边AB上的D点.
(1)试探究线段AC,AB和AD之间的关系,并说明理由;
(2)线段BC,AB和BD之间也有类似的关系吗?
24.如图,某数学兴趣小组利用树影测量树高.已测出树的影长为9 m,并测出此时太阳光线与地面成30°角.
(1)求树AB的高度;
(2)因水土流失,此时树AB沿太阳光线方向倾倒,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.(计算结果精确到0.1米,参照数据≈1.414,≈1.732)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.若木棒长为1.2 m,则它的正投影的长一定( D )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
2.球的正投影是( A )
A.圆面 B.椭圆面 C.点 D.圆环
3.【中考·绥化】正方形的正投影不可能是( D )
A.线段 B.矩形 C.正方形 D.梯形
4.下列投影中,正投影有( B )
A.0个 B.1个 C.2个 D.3个
5.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( D )
6.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( D )
A.AB=CD B.AB≤CD C.AB>CD D.AB≥CD
7.当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( C )
A.200 cm2 B.300 cm2 C.400 cm2 D.600 cm2
8.几何体在平面P的正投影,取决于( A )
①几何体的形状;
②投影面与几何体的位置关系;
③投影面P的大小.
A.①② B.①③ C.②③ D.①②③
【点拨】几何体在平面的正投影与几何体的形状,投影面与几何体的位置关系有关,与投影面的大小无关.
9.如图,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( C )
10.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( B )
A.圆 B.矩形 C.梯形 D.圆柱
11.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( C )
A.变小 B.变大 C.不发生变化 D.无法确定
12.当棱长为10 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( B )
A.10 cm2 B.100 cm2 C.200 cm2 D.300 cm2
二、填空题
13.投影线 于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为 ;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为 ;
(3)当线段垂直于投影面时,它的正投影是 .当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 .
【答案】垂直 相等 线段大于影长 一个点 一样
14.平行于投影面的平行四边形的面积 等于 它的正投影的面积.(填“大于”“小于”或“等于”)
15.如图是一个三棱柱,投影线的方向如箭头所示,它的正投影是下图中的____.(填序号)
【答案】②
16.如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是_____________.
【答案】π
17.如图,正三棱柱的面EFDC∥平面R且AE=EF=AF=2,AB=6,正三棱柱在平面R的正投影是________,正投影的面积为_______.
【答案】矩形 12
18.小明喜欢玩魔方,已知他的魔方的棱长为5.5 cm,若魔方的一面平行于投影面,则这个面的正投影的面积为 cm2.
【答案】30.25
【解析】 根据题意知,魔方的正投影是边长为5.5 cm的正方形,所以正投影的面积为5.5×5.5=30.25(cm2).
三、解答题
19.光线由上到下照射一个三棱柱时的投影如图,三棱柱的高为10.请分别画出三棱柱各个面的正投影,并标出投影的边长.
解:如图
20.已知木棒AB垂直投射于投影面α上的投影为A1B1,且木棒AB的长为8 cm.
(1)如图1,若AB平行于投影面α,求A1B1的长;
(2)如图2,若木棒AB与投影面α的倾斜角为30°,求此时A1B1的长.(结果保留根号)
解:(1)A1B1=AB=8 cm.
(2)过点A作AH⊥BB1,垂足为H.
∵AA1⊥A1B1,BB1⊥A1B1,
∴四边形AA1B1H为矩形,∴AH=A1B1.
在Rt△AHB中,∠BAH=30°,AB=8 cm,
∴AH=AB·cos 30°=8×(cm),
∴此时A1B1的长为4 cm.
21.如图,从热气球P上测得两建筑物A,B的底部的俯视角分别为45°和30°,如果A,B两建筑物的距离为90 m,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果精确到0.1 m,参考数据:≈1.732,≈1.414)
解:过点P作PC⊥AB于点C.
在Rt△ACP中,∠APC=45°,则AC=PC.
在Rt△BCP中,∠B=30°,则BC=PC.
∵AB=AC+BC=(+1)PC=90 m,
∴PC=≈32.9(m).
答:热气球P的高度约为32.9 m.
22.已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD在面β上的正投影,AD,BC与投影面β平行,且AB,CD与投影面β成30°角,求正方形ABCD的正投影的面积.
解:过点A作AH⊥BB1于点H.依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,
∴AH=AB·cos 30°=10×=5(cm),
∴A1B1=AH=5cm.∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5×10=50(cm2),
即正方形ABCD的正投影的面积是50cm2.
【规律总结】求投影的面积,先确定投影的形状,再根据相应的面积公式,有针对性地求出相关线段的长.
23.如图,Rt△ABC中,∠C=90°,在阳光的垂直照射下,点C落在斜边AB上的D点.
(1)试探究线段AC,AB和AD之间的关系,并说明理由;
(2)线段BC,AB和BD之间也有类似的关系吗?
解:当阳光垂直照射时,点C在AB上的正投影是D点,连接CD,
则CD⊥AB.
(1)AC2=AD·AB.
理由:在Rt△ABC和Rt△ACD中,
∠A=∠A,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴,
即AC2=AD·AB.
(2)线段BC,AB和BD之间有类似的关系.
∵△BDC∽△BCA,
∴,
即BC2=AB·BD.
24.如图,某数学兴趣小组利用树影测量树高.已测出树的影长为9 m,并测出此时太阳光线与地面成30°角.
(1)求树AB的高度;
(2)因水土流失,此时树AB沿太阳光线方向倾倒,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.(计算结果精确到0.1米,参照数据≈1.414,≈1.732)
解:(1)在Rt△ABC中,∠BAC=90°,∠BCA=30°,因为tan∠BCA=,
所以AB=AC·tan∠BCA=9×≈5.2(m).
(2)以点A为圆心,以AB长为半径作圆弧,当太阳光线与圆弧相切时,设切点为D,连接AD,则∠DAC=60°,即树与地面的夹角为60°,此时树影最长.设此时树顶端的影子为点E,则DE⊥AD,在Rt△ADE中,∠ADE=90°,∠AED=30°,所以AE=2AD≈2×5.2=10.4(m),即树影的最大长度约为10.4 m.
第2课时 正投影
一、选择题
1.若木棒长为1.2 m,则它的正投影的长一定( )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
2.球的正投影是( )
A.圆面 B.椭圆面 C.点 D.圆环
3.【中考·绥化】正方形的正投影不可能是( )
A.线段 B.矩形 C.正方形 D.梯形
4.下列投影中,正投影有( )
A.0个 B.1个 C.2个 D.3个
5.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( )
6.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( )
A.AB=CD B.AB≤CD C.AB>CD D.AB≥CD
7.当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.200 cm2 B.300 cm2 C.400 cm2 D.600 cm2
8.几何体在平面P的正投影,取决于( )
①几何体的形状;
②投影面与几何体的位置关系;
③投影面P的大小.
A.①② B.①③ C.②③ D.①②③
9.如图,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( )
10.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( )
A.圆 B.矩形 C.梯形 D.圆柱
11.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( )
A.变小 B.变大 C.不发生变化 D.无法确定
12.当棱长为10 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( )
A.10 cm2 B.100 cm2 C.200 cm2 D.300 cm2
二、填空题
13.投影线 于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为 ;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为 ;
(3)当线段垂直于投影面时,它的正投影是 .当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 .
14.平行于投影面的平行四边形的面积 它的正投影的面积.(填“大于”“小于”或“等于”)
15.如图是一个三棱柱,投影线的方向如箭头所示,它的正投影是下图中的____.(填序号)
16.如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是_____________.
17.如图,正三棱柱的面EFDC∥平面R且AE=EF=AF=2,AB=6,正三棱柱在平面R的正投影是________,正投影的面积为_______.
18.小明喜欢玩魔方,已知他的魔方的棱长为5.5 cm,若魔方的一面平行于投影面,则这个面的正投影的面积为 cm2.
三、解答题
19.光线由上到下照射一个三棱柱时的投影如图,三棱柱的高为10.请分别画出三棱柱各个面的正投影,并标出投影的边长.
20.已知木棒AB垂直投射于投影面α上的投影为A1B1,且木棒AB的长为8 cm.
(1)如图1,若AB平行于投影面α,求A1B1的长;
(2)如图2,若木棒AB与投影面α的倾斜角为30°,求此时A1B1的长.(结果保留根号)
21.如图,从热气球P上测得两建筑物A,B的底部的俯视角分别为45°和30°,如果A,B两建筑物的距离为90 m,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果精确到0.1 m,参考数据:≈1.732,≈1.414)
22.已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD在面β上的正投影,AD,BC与投影面β平行,且AB,CD与投影面β成30°角,求正方形ABCD的正投影的面积.
23.如图,Rt△ABC中,∠C=90°,在阳光的垂直照射下,点C落在斜边AB上的D点.
(1)试探究线段AC,AB和AD之间的关系,并说明理由;
(2)线段BC,AB和BD之间也有类似的关系吗?
24.如图,某数学兴趣小组利用树影测量树高.已测出树的影长为9 m,并测出此时太阳光线与地面成30°角.
(1)求树AB的高度;
(2)因水土流失,此时树AB沿太阳光线方向倾倒,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.(计算结果精确到0.1米,参照数据≈1.414,≈1.732)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.若木棒长为1.2 m,则它的正投影的长一定( D )
A.大于1.2 m B.小于1.2 m C.等于1.2 m D.小于或等于1.2 m
2.球的正投影是( A )
A.圆面 B.椭圆面 C.点 D.圆环
3.【中考·绥化】正方形的正投影不可能是( D )
A.线段 B.矩形 C.正方形 D.梯形
4.下列投影中,正投影有( B )
A.0个 B.1个 C.2个 D.3个
5.如图,水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影是( D )
6.一根笔直的小木棒(记为线段AB),它的正投影为线段CD,则下列各式中一定成立的是( D )
A.AB=CD B.AB≤CD C.AB>CD D.AB≥CD
7.当棱长为20 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( C )
A.200 cm2 B.300 cm2 C.400 cm2 D.600 cm2
8.几何体在平面P的正投影,取决于( A )
①几何体的形状;
②投影面与几何体的位置关系;
③投影面P的大小.
A.①② B.①③ C.②③ D.①②③
【点拨】几何体在平面的正投影与几何体的形状,投影面与几何体的位置关系有关,与投影面的大小无关.
9.如图,把正方体一个顶点朝上立放,在它下面放一张白纸,使纸面与太阳光垂直,则正方体在纸上的正投影是( C )
10.如图,箭头表示投影线的方向,则图中圆柱体的正投影是( B )
A.圆 B.矩形 C.梯形 D.圆柱
11.当某一几何体在投影面P前的摆放位置确定以后,改变它与投影面P的距离,其正投影的形状( C )
A.变小 B.变大 C.不发生变化 D.无法确定
12.当棱长为10 cm的正方体的某个面平行于投影面时,这个正方体的正投影的面积为( B )
A.10 cm2 B.100 cm2 C.200 cm2 D.300 cm2
二、填空题
13.投影线 于投影面产生的投影叫做正投影.
(1)当线段平行于投影面时,线段与它的正投影的大小关系为 ;
(2)当线段倾斜于投影面时,线段与它的正投影的大小关系为 ;
(3)当线段垂直于投影面时,它的正投影是 .当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小 .
【答案】垂直 相等 线段大于影长 一个点 一样
14.平行于投影面的平行四边形的面积 等于 它的正投影的面积.(填“大于”“小于”或“等于”)
15.如图是一个三棱柱,投影线的方向如箭头所示,它的正投影是下图中的____.(填序号)
【答案】②
16.如图所示是一个圆锥在某平面上的正投影,则该圆锥的侧面积是_____________.
【答案】π
17.如图,正三棱柱的面EFDC∥平面R且AE=EF=AF=2,AB=6,正三棱柱在平面R的正投影是________,正投影的面积为_______.
【答案】矩形 12
18.小明喜欢玩魔方,已知他的魔方的棱长为5.5 cm,若魔方的一面平行于投影面,则这个面的正投影的面积为 cm2.
【答案】30.25
【解析】 根据题意知,魔方的正投影是边长为5.5 cm的正方形,所以正投影的面积为5.5×5.5=30.25(cm2).
三、解答题
19.光线由上到下照射一个三棱柱时的投影如图,三棱柱的高为10.请分别画出三棱柱各个面的正投影,并标出投影的边长.
解:如图
20.已知木棒AB垂直投射于投影面α上的投影为A1B1,且木棒AB的长为8 cm.
(1)如图1,若AB平行于投影面α,求A1B1的长;
(2)如图2,若木棒AB与投影面α的倾斜角为30°,求此时A1B1的长.(结果保留根号)
解:(1)A1B1=AB=8 cm.
(2)过点A作AH⊥BB1,垂足为H.
∵AA1⊥A1B1,BB1⊥A1B1,
∴四边形AA1B1H为矩形,∴AH=A1B1.
在Rt△AHB中,∠BAH=30°,AB=8 cm,
∴AH=AB·cos 30°=8×(cm),
∴此时A1B1的长为4 cm.
21.如图,从热气球P上测得两建筑物A,B的底部的俯视角分别为45°和30°,如果A,B两建筑物的距离为90 m,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果精确到0.1 m,参考数据:≈1.732,≈1.414)
解:过点P作PC⊥AB于点C.
在Rt△ACP中,∠APC=45°,则AC=PC.
在Rt△BCP中,∠B=30°,则BC=PC.
∵AB=AC+BC=(+1)PC=90 m,
∴PC=≈32.9(m).
答:热气球P的高度约为32.9 m.
22.已知一纸板的形状为正方形ABCD,且边长为10 cm.如图,四边形A1B1C1D1是正方形ABCD在面β上的正投影,AD,BC与投影面β平行,且AB,CD与投影面β成30°角,求正方形ABCD的正投影的面积.
解:过点A作AH⊥BB1于点H.依题意,得∠BAH=30°,四边形A1B1C1D1是矩形,其中A1D1=AD,A1B1=AH.
∵AH⊥BB1,∠BAH=30°,
∴AH=AB·cos 30°=10×=5(cm),
∴A1B1=AH=5cm.∵A1D1=AD=10 cm,
∴S四边形A1B1C1D1=A1B1·A1D1=5×10=50(cm2),
即正方形ABCD的正投影的面积是50cm2.
【规律总结】求投影的面积,先确定投影的形状,再根据相应的面积公式,有针对性地求出相关线段的长.
23.如图,Rt△ABC中,∠C=90°,在阳光的垂直照射下,点C落在斜边AB上的D点.
(1)试探究线段AC,AB和AD之间的关系,并说明理由;
(2)线段BC,AB和BD之间也有类似的关系吗?
解:当阳光垂直照射时,点C在AB上的正投影是D点,连接CD,
则CD⊥AB.
(1)AC2=AD·AB.
理由:在Rt△ABC和Rt△ACD中,
∠A=∠A,∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴,
即AC2=AD·AB.
(2)线段BC,AB和BD之间有类似的关系.
∵△BDC∽△BCA,
∴,
即BC2=AB·BD.
24.如图,某数学兴趣小组利用树影测量树高.已测出树的影长为9 m,并测出此时太阳光线与地面成30°角.
(1)求树AB的高度;
(2)因水土流失,此时树AB沿太阳光线方向倾倒,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.(计算结果精确到0.1米,参照数据≈1.414,≈1.732)
解:(1)在Rt△ABC中,∠BAC=90°,∠BCA=30°,因为tan∠BCA=,
所以AB=AC·tan∠BCA=9×≈5.2(m).
(2)以点A为圆心,以AB长为半径作圆弧,当太阳光线与圆弧相切时,设切点为D,连接AD,则∠DAC=60°,即树与地面的夹角为60°,此时树影最长.设此时树顶端的影子为点E,则DE⊥AD,在Rt△ADE中,∠ADE=90°,∠AED=30°,所以AE=2AD≈2×5.2=10.4(m),即树影的最大长度约为10.4 m.
