29.3 课题学习 制作立体模型同步练习(含答案)
文档属性
| 名称 | 29.3 课题学习 制作立体模型同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 19:00:37 | ||
图片预览

文档简介
29.3 课题学习 制作立体模型
一、选择题
1.如图是某几何体的三视图,该几何体是( )
A.长方体 B.正方体 C.三棱锥 D.三棱柱
2.如图是某一个多面体的表面展开图,那么这个多面体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3.下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( )
A.①② B.③④ C.② D.③
4.一个几何体的三视图如图,那么这个几何体是( )
5.【2021·荆门】如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )
A.传 B.因 C.承 D.基
6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.下面的图形经过折叠可以围成一个棱柱的是( )
8.下列图形经过折叠不能围成一个棱柱的是( )
9.如图所示,正方体的展开图为( )
10.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法共有( )
A.7种 B.4种 C.3种 D.2种
11.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
二、填空题
12.如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 .
13.小明用彩纸给爸爸做了一顶圆锥形生日帽,其左视图和俯视图如图所示,其中点C到AB的距离为12 cm,☉C'的周长为24π,则至少需用彩纸 cm2.(接口处重叠面积不计,结果保留π)
14.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法有 种.
15.如图是一个几何体的三视图,那么这个几何体是_____________.
三、解答题
16.一个几何体的三视图如图所示,若其俯视图为正方形,求这个几何体的体积.
17.按照下面给出的两组视图:
选取合适的材料制成相应的实物模型,写出制作流程.
18.(1)请画出该立体模型的三视图和表面展开图;
(2)做该笔筒至少要用多少平方厘米的废纸板?
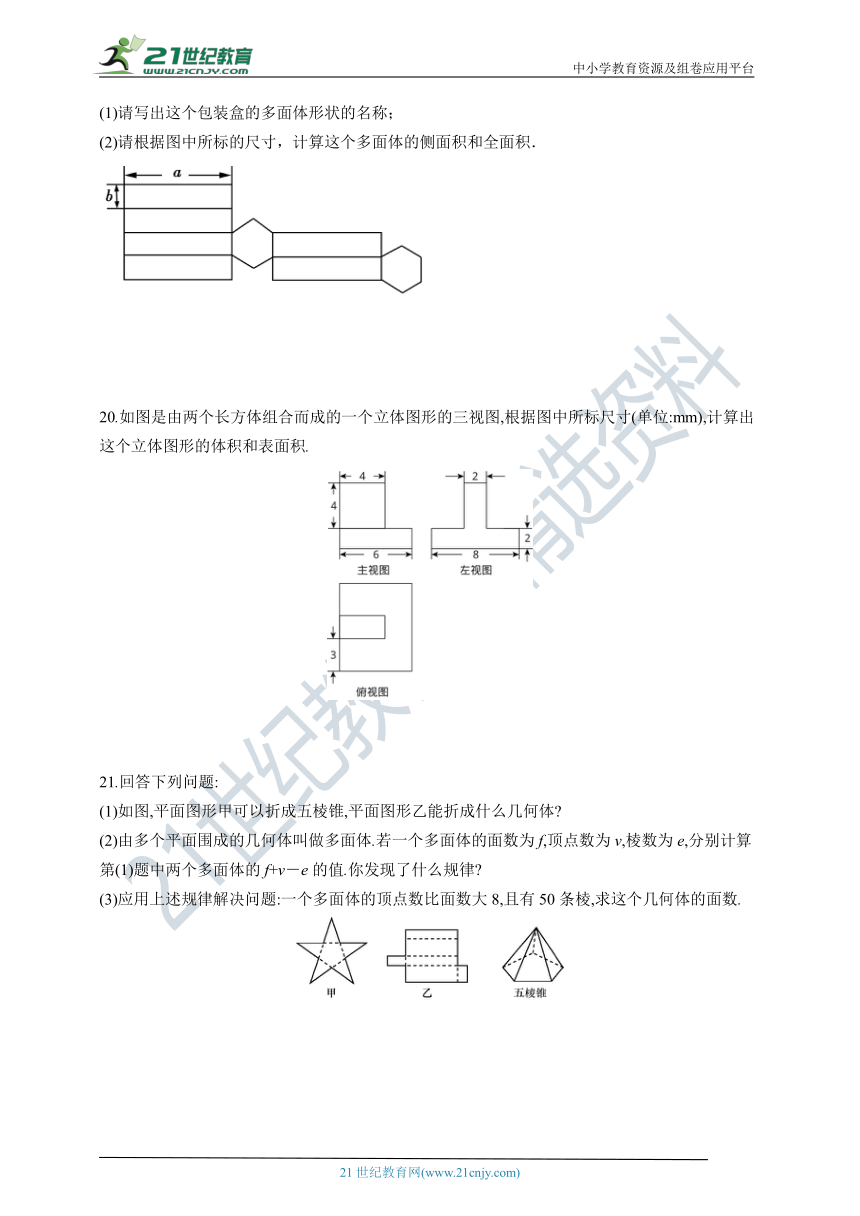
19.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.
20.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的体积和表面积.
21.回答下列问题:
(1)如图,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图是某几何体的三视图,该几何体是( D )
A.长方体 B.正方体 C.三棱锥 D.三棱柱
2.如图是某一个多面体的表面展开图,那么这个多面体是( D )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3.下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( C )
A.①② B.③④ C.② D.③
4.一个几何体的三视图如图,那么这个几何体是( A )
5.【2021·荆门】如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( D )
A.传 B.因 C.承 D.基
6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是( A )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.下面的图形经过折叠可以围成一个棱柱的是( B )
【解析】 选项A有四个侧面,所以上下两个面应该为四边形;选项C有四个侧面,上、下两个面应该为四边形且居两侧;选项D缺少两个底面.
8.下列图形经过折叠不能围成一个棱柱的是( D )
9.如图所示,正方体的展开图为( A )
10.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法共有( B )
A.7种 B.4种 C.3种 D.2种
11.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( C )
A.24 B.25 C.26 D.27
【解析】 由俯视图得最底层有7个小正方体,由主视图和左视图得第二层有2个小正方体,第三层有1个小正方体,则小正方体分布情况如图所示,所以该几何体共由10个小正方体搭成.若搭成一个大长方体,则至少还需要小正方体的个数为3×4×3-10=26.
二、填空题
12.如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 400cm3 .
13.小明用彩纸给爸爸做了一顶圆锥形生日帽,其左视图和俯视图如图所示,其中点C到AB的距离为12 cm,☉C'的周长为24π,则至少需用彩纸 cm2.(接口处重叠面积不计,结果保留π)
【答案】288π
【解析】 由题意可得,圆锥底面周长为24π cm,所以圆锥底面圆的半径为12 cm,又高为12 cm,所以母线长为=24(cm),所以该圆锥的侧面积为×24π×24=288π(cm2),即至少需用彩纸288π cm2.
14.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法有 种.
【答案】4
15.如图是一个几何体的三视图,那么这个几何体是_____________.
【答案】四棱柱
三、解答题
16.一个几何体的三视图如图所示,若其俯视图为正方形,求这个几何体的体积.
解:观察该几何体及其三视图发现,该几何体的底面是正方形,且边长为×3=6.
17.按照下面给出的两组视图:
选取合适的材料制成相应的实物模型,写出制作流程.
解:(1)是圆锥.制作流程:①用刻度尺度量其底面圆的半径r,高h;②用小刀把萝卜削成一个底面圆的半径为r,高为h的圆柱体;③把圆柱体加工成如图①所示的模型.
(2)为正方体截去一个三棱柱,是五棱柱.制作流程:①用刻度尺度量正方体的棱长a,被截去的三棱柱的底面为直角三角形,一条直角边长为b,另一条直角边长为c;②用小刀将萝卜削成一个正方体,棱长为a;③在以这个正方体为毛坯的基础上再加工,使其截去一个三棱
柱,三棱柱底面上直角三角形的两直角边长
分别为b和c,做成如图②所示的模型.
【点拨】由三视图得出几何体,图(1)是圆锥,图(2)为正方体截去一个三棱柱,是五棱柱.
【规律总结】(1)选取材料要易切割;(2)由三视图画出几何体模型,再将模型上有关尺寸用刻度尺量出;(3)制作毛坯,再从毛坯中加工成符合条件的立体模型.
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.
18.(1)请画出该立体模型的三视图和表面展开图;
解:三视图和表面展开图如图(表面展开图画法不唯一):
(2)做该笔筒至少要用多少平方厘米的废纸板?
解:侧面积为(6+8+10)×14=336(cm2),
易知底面为直角三角形,
直角三角形的面积为×8×6=24(cm2),
表面积为336+24=360(cm2).
所以做该笔筒至少要用废纸板360 cm2.
19.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.
解:(1)六棱柱 (2)侧面积6ab,全面积6ab+3b2
20.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的体积和表面积.
解:根据三视图可得上面的长方体长4 mm、高4 mm、宽2 mm,下面的长方体长6 mm、宽8 mm、高2 mm,
∴立体图形的体积是4×4×2+6×8×2=128(mm3),
立体图形的表面积是4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
21.回答下列问题:
(1)如图,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
解:(1)平面图形乙能折成长方体.
(2)甲:f=6,v=6,e=10,f+v-e=2;
乙:f=6,v=8,e=12,f+v-e=2.
规律:面数+顶点数-棱数=2.
(3)设这个多面体的面数为x.
由题可得x+x+8-50=2,解得x=22,
∴这个几何体的面数为22.
一、选择题
1.如图是某几何体的三视图,该几何体是( )
A.长方体 B.正方体 C.三棱锥 D.三棱柱
2.如图是某一个多面体的表面展开图,那么这个多面体是( )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3.下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( )
A.①② B.③④ C.② D.③
4.一个几何体的三视图如图,那么这个几何体是( )
5.【2021·荆门】如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( )
A.传 B.因 C.承 D.基
6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是( )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.下面的图形经过折叠可以围成一个棱柱的是( )
8.下列图形经过折叠不能围成一个棱柱的是( )
9.如图所示,正方体的展开图为( )
10.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法共有( )
A.7种 B.4种 C.3种 D.2种
11.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( )
A.24 B.25 C.26 D.27
二、填空题
12.如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 .
13.小明用彩纸给爸爸做了一顶圆锥形生日帽,其左视图和俯视图如图所示,其中点C到AB的距离为12 cm,☉C'的周长为24π,则至少需用彩纸 cm2.(接口处重叠面积不计,结果保留π)
14.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法有 种.
15.如图是一个几何体的三视图,那么这个几何体是_____________.
三、解答题
16.一个几何体的三视图如图所示,若其俯视图为正方形,求这个几何体的体积.
17.按照下面给出的两组视图:
选取合适的材料制成相应的实物模型,写出制作流程.
18.(1)请画出该立体模型的三视图和表面展开图;
(2)做该笔筒至少要用多少平方厘米的废纸板?
19.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.
20.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的体积和表面积.
21.回答下列问题:
(1)如图,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.如图是某几何体的三视图,该几何体是( D )
A.长方体 B.正方体 C.三棱锥 D.三棱柱
2.如图是某一个多面体的表面展开图,那么这个多面体是( D )
A.四棱锥 B.四棱柱 C.三棱锥 D.三棱柱
3.下列四组图中,每组左边的平面图形能够折叠成右边的立体图形的是( C )
A.①② B.③④ C.② D.③
4.一个几何体的三视图如图,那么这个几何体是( A )
5.【2021·荆门】如图是一个正方体的平面展开图,把展开图折叠成正方体后,“红”字的面的对面上的字是( D )
A.传 B.因 C.承 D.基
6.把如图所示的纸片沿着虚线折叠,可以得到的几何体是( A )
A.三棱柱 B.四棱柱 C.三棱锥 D.四棱锥
7.下面的图形经过折叠可以围成一个棱柱的是( B )
【解析】 选项A有四个侧面,所以上下两个面应该为四边形;选项C有四个侧面,上、下两个面应该为四边形且居两侧;选项D缺少两个底面.
8.下列图形经过折叠不能围成一个棱柱的是( D )
9.如图所示,正方体的展开图为( A )
10.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法共有( B )
A.7种 B.4种 C.3种 D.2种
11.如图是由一些棱长为1的小正方体搭成的几何体的三视图.若在所搭几何体的基础上(不改变原几何体中小正方体的位置),继续添加相同的小正方体,以搭成一个长方体,至少还需要小正方体的个数为( C )
A.24 B.25 C.26 D.27
【解析】 由俯视图得最底层有7个小正方体,由主视图和左视图得第二层有2个小正方体,第三层有1个小正方体,则小正方体分布情况如图所示,所以该几何体共由10个小正方体搭成.若搭成一个大长方体,则至少还需要小正方体的个数为3×4×3-10=26.
二、填空题
12.如图1,在边长为18 cm的正方形纸片的四个角各剪去一个同样大小的正方形,折成一个如图2所示的无盖的长方体.设剪去的小正方形的边长为4 cm,则折成的无盖长方体的容积是 400cm3 .
13.小明用彩纸给爸爸做了一顶圆锥形生日帽,其左视图和俯视图如图所示,其中点C到AB的距离为12 cm,☉C'的周长为24π,则至少需用彩纸 cm2.(接口处重叠面积不计,结果保留π)
【答案】288π
【解析】 由题意可得,圆锥底面周长为24π cm,所以圆锥底面圆的半径为12 cm,又高为12 cm,所以母线长为=24(cm),所以该圆锥的侧面积为×24π×24=288π(cm2),即至少需用彩纸288π cm2.
14.在图中添加一个小正方形,使该图形经过折叠后能围成一个四棱柱,不同的添法有 种.
【答案】4
15.如图是一个几何体的三视图,那么这个几何体是_____________.
【答案】四棱柱
三、解答题
16.一个几何体的三视图如图所示,若其俯视图为正方形,求这个几何体的体积.
解:观察该几何体及其三视图发现,该几何体的底面是正方形,且边长为×3=6.
17.按照下面给出的两组视图:
选取合适的材料制成相应的实物模型,写出制作流程.
解:(1)是圆锥.制作流程:①用刻度尺度量其底面圆的半径r,高h;②用小刀把萝卜削成一个底面圆的半径为r,高为h的圆柱体;③把圆柱体加工成如图①所示的模型.
(2)为正方体截去一个三棱柱,是五棱柱.制作流程:①用刻度尺度量正方体的棱长a,被截去的三棱柱的底面为直角三角形,一条直角边长为b,另一条直角边长为c;②用小刀将萝卜削成一个正方体,棱长为a;③在以这个正方体为毛坯的基础上再加工,使其截去一个三棱
柱,三棱柱底面上直角三角形的两直角边长
分别为b和c,做成如图②所示的模型.
【点拨】由三视图得出几何体,图(1)是圆锥,图(2)为正方体截去一个三棱柱,是五棱柱.
【规律总结】(1)选取材料要易切割;(2)由三视图画出几何体模型,再将模型上有关尺寸用刻度尺量出;(3)制作毛坯,再从毛坯中加工成符合条件的立体模型.
小明利用废纸板做一个三棱柱形无盖的笔筒,设计三棱柱立体模型如图所示,有关数据已标注在图上.
18.(1)请画出该立体模型的三视图和表面展开图;
解:三视图和表面展开图如图(表面展开图画法不唯一):
(2)做该笔筒至少要用多少平方厘米的废纸板?
解:侧面积为(6+8+10)×14=336(cm2),
易知底面为直角三角形,
直角三角形的面积为×8×6=24(cm2),
表面积为336+24=360(cm2).
所以做该笔筒至少要用废纸板360 cm2.
19.如图是一个食品包装盒的侧面展开图.
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积.
解:(1)六棱柱 (2)侧面积6ab,全面积6ab+3b2
20.如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),计算出这个立体图形的体积和表面积.
解:根据三视图可得上面的长方体长4 mm、高4 mm、宽2 mm,下面的长方体长6 mm、宽8 mm、高2 mm,
∴立体图形的体积是4×4×2+6×8×2=128(mm3),
立体图形的表面积是4×4×2+4×2×2+4×2+6×2×2+8×2×2+6×8×2-4×2=200(mm2).
21.回答下列问题:
(1)如图,平面图形甲可以折成五棱锥,平面图形乙能折成什么几何体
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点数为v,棱数为e,分别计算第(1)题中两个多面体的f+v-e的值.你发现了什么规律
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
解:(1)平面图形乙能折成长方体.
(2)甲:f=6,v=6,e=10,f+v-e=2;
乙:f=6,v=8,e=12,f+v-e=2.
规律:面数+顶点数-棱数=2.
(3)设这个多面体的面数为x.
由题可得x+x+8-50=2,解得x=22,
∴这个几何体的面数为22.
