第29章 投影与视图章末复习题(含答案)
图片预览
文档简介
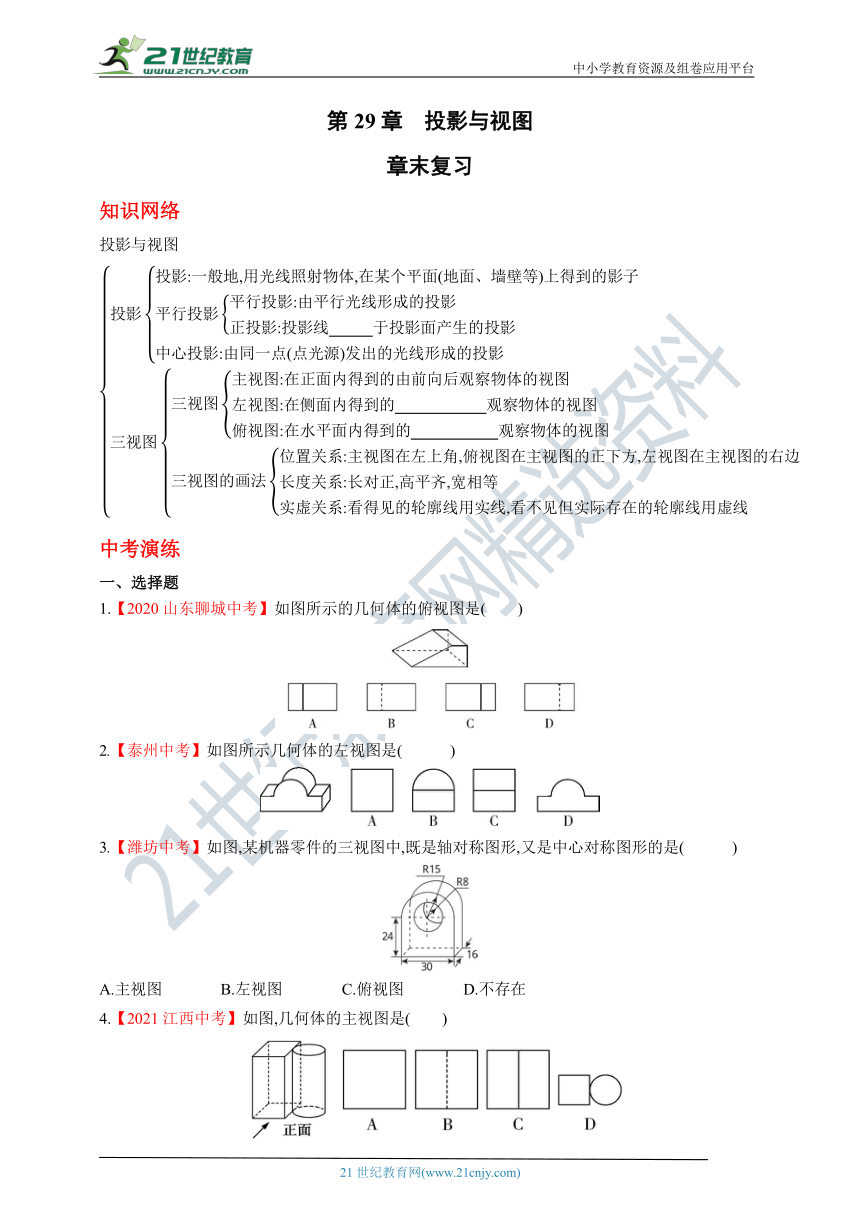
第29章 投影与视图
章末复习
知识网络
投影与视图
中考演练
一、选择题
1.【2020山东聊城中考】如图所示的几何体的俯视图是( )
2.【泰州中考】如图所示几何体的左视图是( )
3.【潍坊中考】如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
A.主视图 B.左视图 C.俯视图 D.不存在
4.【2021江西中考】如图,几何体的主视图是( )
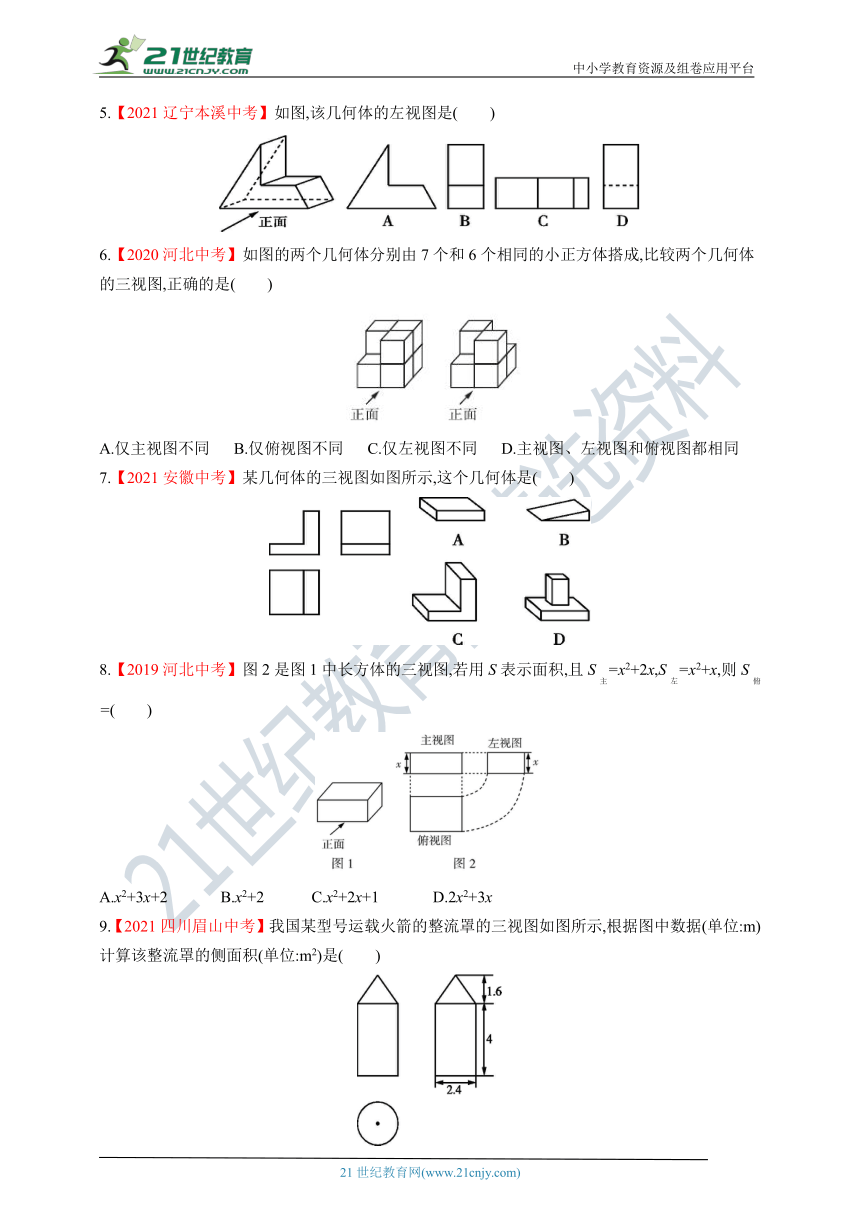
5.【2021辽宁本溪中考】如图,该几何体的左视图是( )
6.【2020河北中考】如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A.仅主视图不同 B.仅俯视图不同 C.仅左视图不同 D.主视图、左视图和俯视图都相同
7.【2021安徽中考】某几何体的三视图如图所示,这个几何体是( )
8.【2019河北中考】图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯=( )
A.x2+3x+2 B.x2+2 C.x2+2x+1 D.2x2+3x
9.【2021四川眉山中考】我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:m)计算该整流罩的侧面积(单位:m2)是( )
A.7.2π B.11.52π C.12π D.13.44π
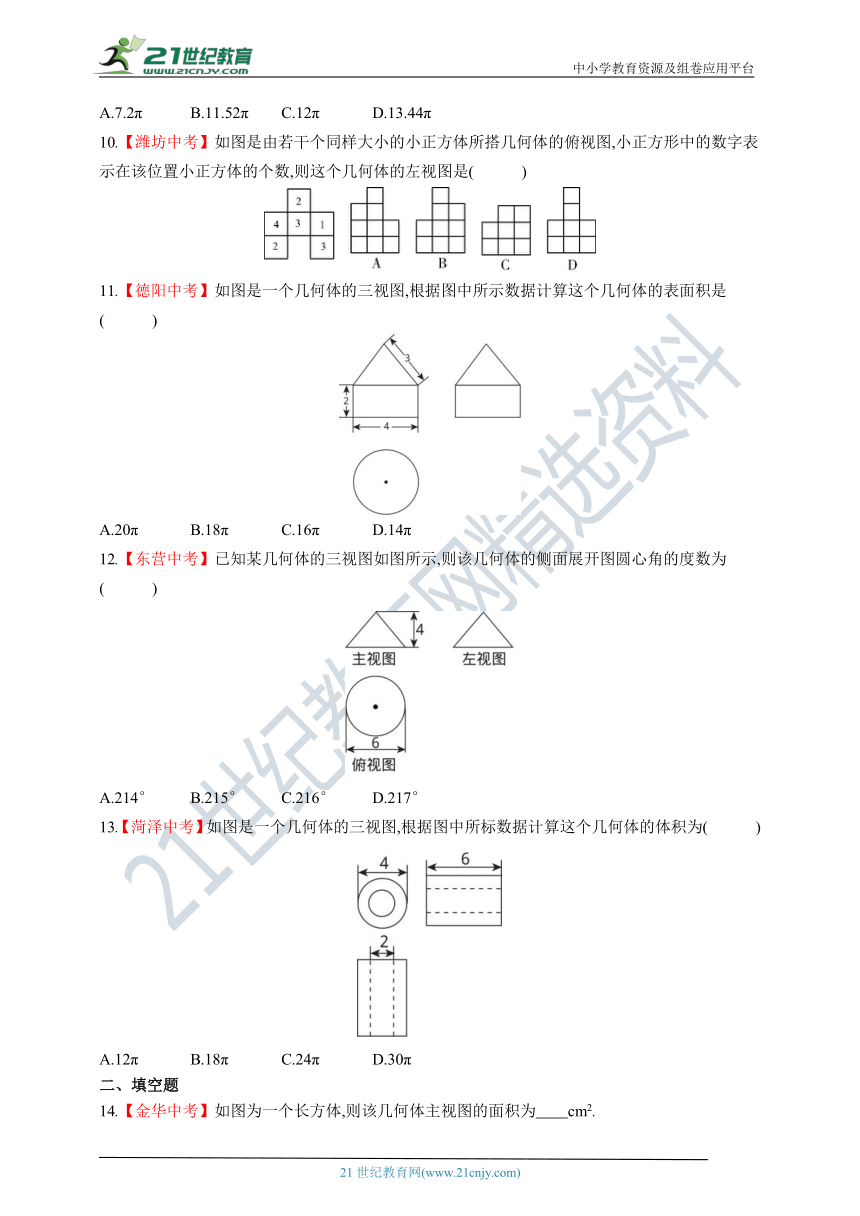
10.【潍坊中考】如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
11.【德阳中考】如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )
A.20π B.18π C.16π D.14π
12.【东营中考】已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )
A.214° B.215° C.216° D.217°
13.【菏泽中考】如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A.12π B.18π C.24π D.30π
二、填空题
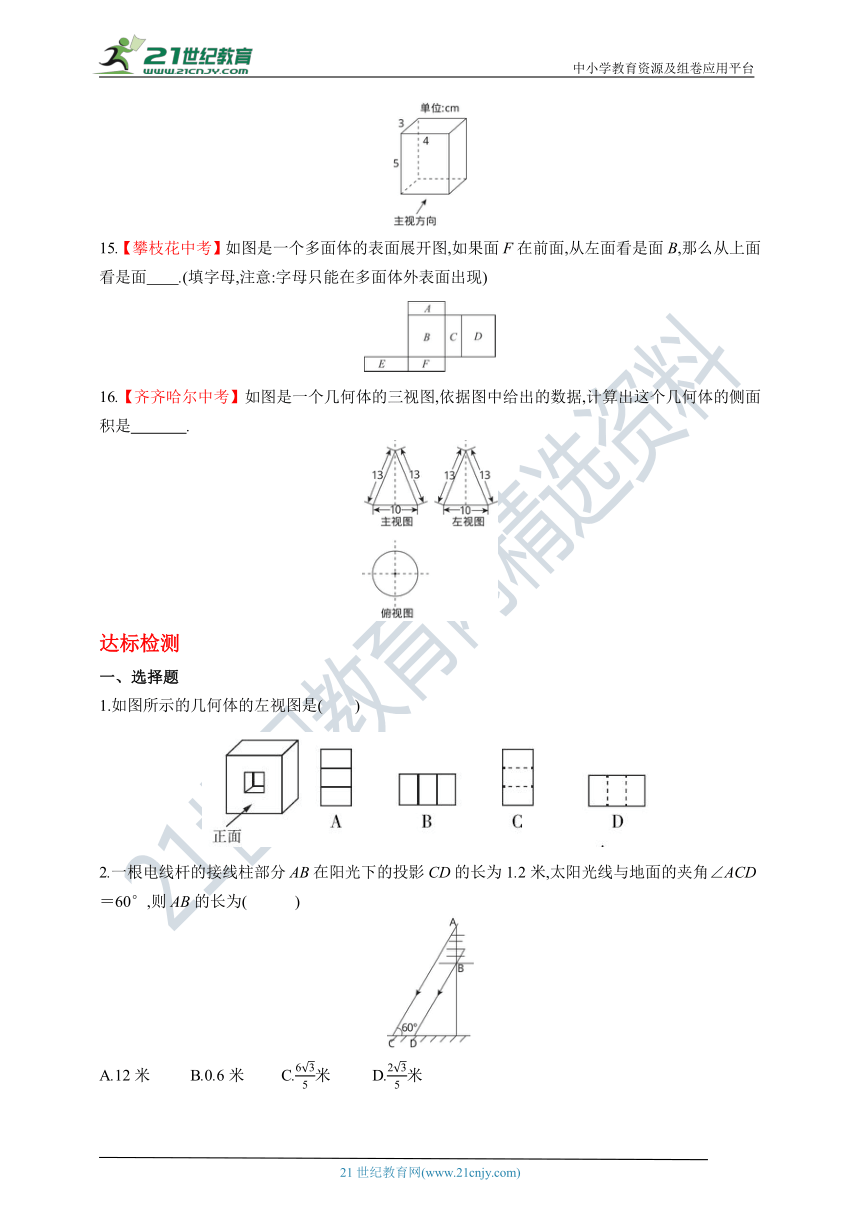
14.【金华中考】如图为一个长方体,则该几何体主视图的面积为 cm2.
15.【攀枝花中考】如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 .(填字母,注意:字母只能在多面体外表面出现)
16.【齐齐哈尔中考】如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是 .
达标检测
一、选择题
1.如图所示的几何体的左视图是( )
2.一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.12米 B.0.6米 C.米 D.米
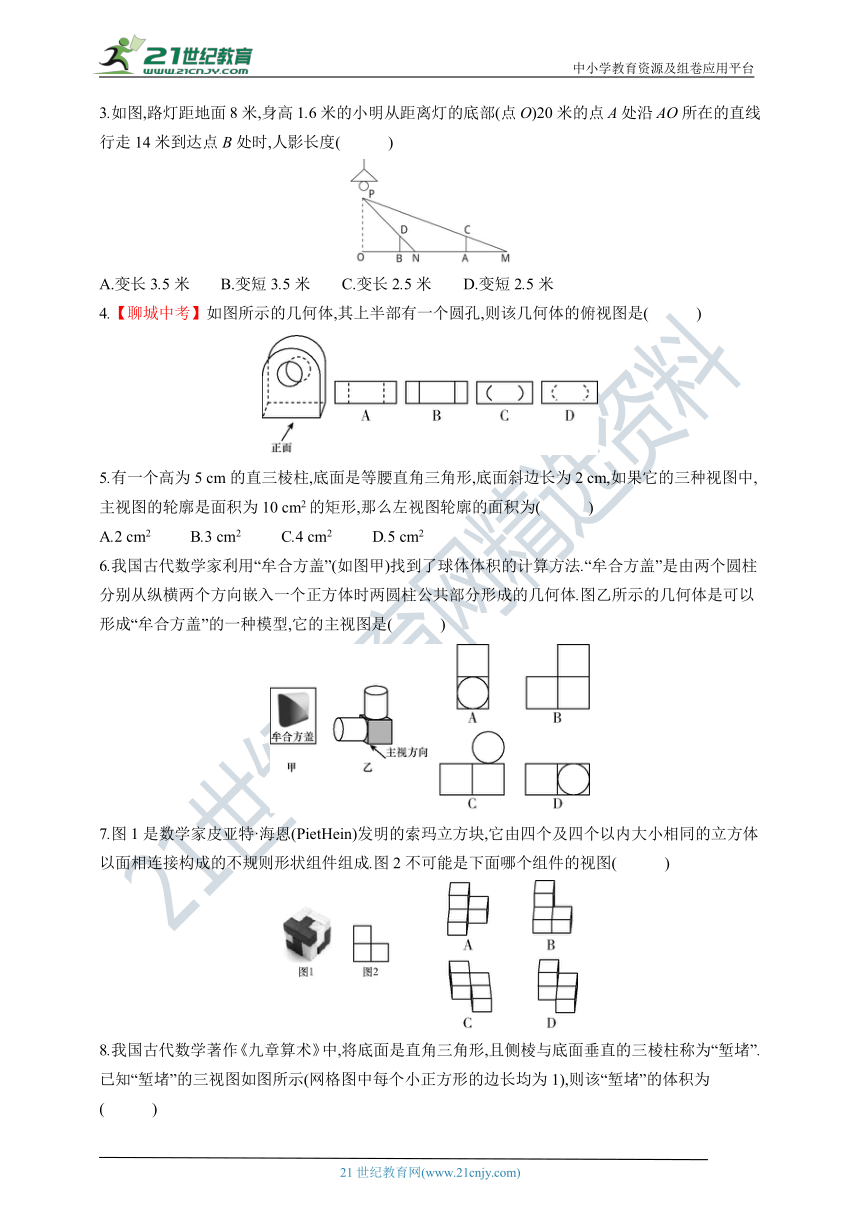
3.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处沿AO所在的直线行走14米到达点B处时,人影长度( )
A.变长3.5米 B.变短3.5米 C.变长2.5米 D.变短2.5米
4.【聊城中考】如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( )
5.有一个高为5 cm的直三棱柱,底面是等腰直角三角形,底面斜边长为2 cm,如果它的三种视图中,主视图的轮廓是面积为10 cm2的矩形,那么左视图轮廓的面积为( )
A.2 cm2 B.3 cm2 C.4 cm2 D.5 cm2
6.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
7.图1是数学家皮亚特·海恩(PietHein)发明的索玛立方块,它由四个及四个以内大小相同的立方体以面相连接构成的不规则形状组件组成.图2不可能是下面哪个组件的视图( )
8.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( )
A.16+16 B.16+8 C.24+16 D.16
9.如图,在平面直角坐标系中,点P(2,2)处有一个光源.木杆AB两端的坐标分别为A(0,1),B(3,1).则在此光源下,木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
二、填空题
10.小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 m2.(楼之间的距离为20 m)
11.如图所示的几何体中,主视图与左视图都是长方形的是 .
12.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则A容器中水会 .(填“溢出”“刚好”或“未装满”)
三、解答题
13.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB,CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
14.在主视图和俯视图上标出点A,B,C,D的位置.
15.如图是某工件的三视图,求此工件的表面积和体积.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
知识网络
投影与视图
中考演练
一、选择题
1.【2020山东聊城中考】如图所示的几何体的俯视图是( C )
2.【泰州中考】如图所示几何体的左视图是( C )
3.【潍坊中考】如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( C )
A.主视图 B.左视图 C.俯视图 D.不存在
4.【2021江西中考】如图,几何体的主视图是( C )
5.【2021辽宁本溪中考】如图,该几何体的左视图是( D )
【解析】 从左面看该几何体所得到的图形是一个长方形,里面有一条虚线.
6.【2020河北中考】如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( D )
A.仅主视图不同 B.仅俯视图不同 C.仅左视图不同 D.主视图、左视图和俯视图都相同
【解析】 这两个几何体的主视图、左视图和俯视图均为
.
7.【2021安徽中考】某几何体的三视图如图所示,这个几何体是( C )
【解析】 从几何体正面看得到的图形像一个反向的“L”,可排除A,B,D选项.
8.【2019河北中考】图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯=( A )
A.x2+3x+2 B.x2+2 C.x2+2x+1 D.2x2+3x
【解析】 因为S主=x2+2x=x(x+2),S左=x2+x=x(x+1),所以俯视图的长为x+2,宽为x+1,
所以S俯=(x+2)(x+1)=x2+3x+2.
9.【2021四川眉山中考】我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:m)计算该整流罩的侧面积(单位:m2)是( C )
A.7.2π B.11.52π C.12π D.13.44π
【解析】 观察图形可知,该整流罩由圆锥和圆柱组成,且圆锥的母线长为=2(m),所以该整流罩的侧面积为×π×2.4×2+π×2.4×4=12π(m2).
10.【潍坊中考】如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( B )
11.【德阳中考】如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( B )
A.20π B.18π C.16π D.14π
12.【东营中考】已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( C )
A.214° B.215° C.216° D.217°
13.【菏泽中考】如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( B )
A.12π B.18π C.24π D.30π
二、填空题
14.【金华中考】如图为一个长方体,则该几何体主视图的面积为 20 cm2.
15.【攀枝花中考】如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 E .(填字母,注意:字母只能在多面体外表面出现)
16.【齐齐哈尔中考】如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是 65π .
达标检测
一、选择题
1.如图所示的几何体的左视图是( C )
2.一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( C )
A.12米 B.0.6米 C.米 D.米
3.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处沿AO所在的直线行走14米到达点B处时,人影长度( B )
A.变长3.5米 B.变短3.5米 C.变长2.5米 D.变短2.5米
4.【聊城中考】如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( A )
5.有一个高为5 cm的直三棱柱,底面是等腰直角三角形,底面斜边长为2 cm,如果它的三种视图中,主视图的轮廓是面积为10 cm2的矩形,那么左视图轮廓的面积为( D )
A.2 cm2 B.3 cm2 C.4 cm2 D.5 cm2
6.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( B )
7.图1是数学家皮亚特·海恩(PietHein)发明的索玛立方块,它由四个及四个以内大小相同的立方体以面相连接构成的不规则形状组件组成.图2不可能是下面哪个组件的视图( C )
8.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( D )
A.16+16 B.16+8 C.24+16 D.16
9.如图,在平面直角坐标系中,点P(2,2)处有一个光源.木杆AB两端的坐标分别为A(0,1),B(3,1).则在此光源下,木杆AB在x轴上的投影长为( C )
A.3 B.5 C.6 D.7
【解析】 如图,延长PA,PB分别交x轴于点A',B',则木杆AB在x轴上的投影为A'B'.过点P作PE⊥x轴于点E,交AB于点D.∵P(2,2),A(0,1),B(3,1),∴PD=1,PE=2,AB=3.∵AB∥A'B',∴△PAB∽△PA'B',又PD,PE分别是△PAB,△PA'B'的高,∴=,即=,∴A'B'=6.
二、填空题
10.小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 108 m2.(楼之间的距离为20 m)
11.如图所示的几何体中,主视图与左视图都是长方形的是 ①③④ .
12.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则A容器中水会 未装满 .(填“溢出”“刚好”或“未装满”)
三、解答题
13.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB,CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
解:过点B作BH⊥CC1于点H.
∵∠BCC1=45°,∴BH=.
由题知B1C1=BH=,C1D1=CD=5,
∴四边形A1B1C1D1的面积=(cm2).
14.在主视图和俯视图上标出点A,B,C,D的位置.
略
15.如图是某工件的三视图,求此工件的表面积和体积.
解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体.母线长为l=(cm),
S=)π(cm2),
V=×π×(20÷2)2×30=1000 π(cm3).
故此工件的表面积是100(1+)π cm2,体积是1000π cm3.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
【解析】 如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴=,
=,解得x=4.4.
答:围墙AB的高度是4.4 m.
章末复习
知识网络
投影与视图
中考演练
一、选择题
1.【2020山东聊城中考】如图所示的几何体的俯视图是( )
2.【泰州中考】如图所示几何体的左视图是( )
3.【潍坊中考】如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( )
A.主视图 B.左视图 C.俯视图 D.不存在
4.【2021江西中考】如图,几何体的主视图是( )
5.【2021辽宁本溪中考】如图,该几何体的左视图是( )
6.【2020河北中考】如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )
A.仅主视图不同 B.仅俯视图不同 C.仅左视图不同 D.主视图、左视图和俯视图都相同
7.【2021安徽中考】某几何体的三视图如图所示,这个几何体是( )
8.【2019河北中考】图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯=( )
A.x2+3x+2 B.x2+2 C.x2+2x+1 D.2x2+3x
9.【2021四川眉山中考】我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:m)计算该整流罩的侧面积(单位:m2)是( )
A.7.2π B.11.52π C.12π D.13.44π
10.【潍坊中考】如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( )
11.【德阳中考】如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( )
A.20π B.18π C.16π D.14π
12.【东营中考】已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( )
A.214° B.215° C.216° D.217°
13.【菏泽中考】如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A.12π B.18π C.24π D.30π
二、填空题
14.【金华中考】如图为一个长方体,则该几何体主视图的面积为 cm2.
15.【攀枝花中考】如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 .(填字母,注意:字母只能在多面体外表面出现)
16.【齐齐哈尔中考】如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是 .
达标检测
一、选择题
1.如图所示的几何体的左视图是( )
2.一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
A.12米 B.0.6米 C.米 D.米
3.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处沿AO所在的直线行走14米到达点B处时,人影长度( )
A.变长3.5米 B.变短3.5米 C.变长2.5米 D.变短2.5米
4.【聊城中考】如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( )
5.有一个高为5 cm的直三棱柱,底面是等腰直角三角形,底面斜边长为2 cm,如果它的三种视图中,主视图的轮廓是面积为10 cm2的矩形,那么左视图轮廓的面积为( )
A.2 cm2 B.3 cm2 C.4 cm2 D.5 cm2
6.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
7.图1是数学家皮亚特·海恩(PietHein)发明的索玛立方块,它由四个及四个以内大小相同的立方体以面相连接构成的不规则形状组件组成.图2不可能是下面哪个组件的视图( )
8.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( )
A.16+16 B.16+8 C.24+16 D.16
9.如图,在平面直角坐标系中,点P(2,2)处有一个光源.木杆AB两端的坐标分别为A(0,1),B(3,1).则在此光源下,木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
二、填空题
10.小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 m2.(楼之间的距离为20 m)
11.如图所示的几何体中,主视图与左视图都是长方形的是 .
12.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则A容器中水会 .(填“溢出”“刚好”或“未装满”)
三、解答题
13.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB,CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
14.在主视图和俯视图上标出点A,B,C,D的位置.
15.如图是某工件的三视图,求此工件的表面积和体积.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
知识网络
投影与视图
中考演练
一、选择题
1.【2020山东聊城中考】如图所示的几何体的俯视图是( C )
2.【泰州中考】如图所示几何体的左视图是( C )
3.【潍坊中考】如图,某机器零件的三视图中,既是轴对称图形,又是中心对称图形的是( C )
A.主视图 B.左视图 C.俯视图 D.不存在
4.【2021江西中考】如图,几何体的主视图是( C )
5.【2021辽宁本溪中考】如图,该几何体的左视图是( D )
【解析】 从左面看该几何体所得到的图形是一个长方形,里面有一条虚线.
6.【2020河北中考】如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( D )
A.仅主视图不同 B.仅俯视图不同 C.仅左视图不同 D.主视图、左视图和俯视图都相同
【解析】 这两个几何体的主视图、左视图和俯视图均为
.
7.【2021安徽中考】某几何体的三视图如图所示,这个几何体是( C )
【解析】 从几何体正面看得到的图形像一个反向的“L”,可排除A,B,D选项.
8.【2019河北中考】图2是图1中长方体的三视图,若用S表示面积,且S主=x2+2x,S左=x2+x,则S俯=( A )
A.x2+3x+2 B.x2+2 C.x2+2x+1 D.2x2+3x
【解析】 因为S主=x2+2x=x(x+2),S左=x2+x=x(x+1),所以俯视图的长为x+2,宽为x+1,
所以S俯=(x+2)(x+1)=x2+3x+2.
9.【2021四川眉山中考】我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:m)计算该整流罩的侧面积(单位:m2)是( C )
A.7.2π B.11.52π C.12π D.13.44π
【解析】 观察图形可知,该整流罩由圆锥和圆柱组成,且圆锥的母线长为=2(m),所以该整流罩的侧面积为×π×2.4×2+π×2.4×4=12π(m2).
10.【潍坊中考】如图是由若干个同样大小的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数,则这个几何体的左视图是( B )
11.【德阳中考】如图是一个几何体的三视图,根据图中所示数据计算这个几何体的表面积是( B )
A.20π B.18π C.16π D.14π
12.【东营中考】已知某几何体的三视图如图所示,则该几何体的侧面展开图圆心角的度数为( C )
A.214° B.215° C.216° D.217°
13.【菏泽中考】如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( B )
A.12π B.18π C.24π D.30π
二、填空题
14.【金华中考】如图为一个长方体,则该几何体主视图的面积为 20 cm2.
15.【攀枝花中考】如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面 E .(填字母,注意:字母只能在多面体外表面出现)
16.【齐齐哈尔中考】如图是一个几何体的三视图,依据图中给出的数据,计算出这个几何体的侧面积是 65π .
达标检测
一、选择题
1.如图所示的几何体的左视图是( C )
2.一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( C )
A.12米 B.0.6米 C.米 D.米
3.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处沿AO所在的直线行走14米到达点B处时,人影长度( B )
A.变长3.5米 B.变短3.5米 C.变长2.5米 D.变短2.5米
4.【聊城中考】如图所示的几何体,其上半部有一个圆孔,则该几何体的俯视图是( A )
5.有一个高为5 cm的直三棱柱,底面是等腰直角三角形,底面斜边长为2 cm,如果它的三种视图中,主视图的轮廓是面积为10 cm2的矩形,那么左视图轮廓的面积为( D )
A.2 cm2 B.3 cm2 C.4 cm2 D.5 cm2
6.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.图乙所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( B )
7.图1是数学家皮亚特·海恩(PietHein)发明的索玛立方块,它由四个及四个以内大小相同的立方体以面相连接构成的不规则形状组件组成.图2不可能是下面哪个组件的视图( C )
8.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”.已知“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的体积为( D )
A.16+16 B.16+8 C.24+16 D.16
9.如图,在平面直角坐标系中,点P(2,2)处有一个光源.木杆AB两端的坐标分别为A(0,1),B(3,1).则在此光源下,木杆AB在x轴上的投影长为( C )
A.3 B.5 C.6 D.7
【解析】 如图,延长PA,PB分别交x轴于点A',B',则木杆AB在x轴上的投影为A'B'.过点P作PE⊥x轴于点E,交AB于点D.∵P(2,2),A(0,1),B(3,1),∴PD=1,PE=2,AB=3.∵AB∥A'B',∴△PAB∽△PA'B',又PD,PE分别是△PAB,△PA'B'的高,∴=,即=,∴A'B'=6.
二、填空题
10.小芳的房间有一个面积为3 m2的玻璃窗,她站在室内离窗子4 m的地方向外看,她能看到窗前面一幢楼房的面积有 108 m2.(楼之间的距离为20 m)
11.如图所示的几何体中,主视图与左视图都是长方形的是 ①③④ .
12.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,则A容器中水会 未装满 .(填“溢出”“刚好”或“未装满”)
三、解答题
13.如图,正方形纸板ABCD在投影面α上的正投影为A1B1C1D1,其中边AB,CD与投影面平行,AD,BC与投影面不平行.若正方形ABCD的边长为5 cm,∠BCC1=45°,求其投影A1B1C1D1的面积.
解:过点B作BH⊥CC1于点H.
∵∠BCC1=45°,∴BH=.
由题知B1C1=BH=,C1D1=CD=5,
∴四边形A1B1C1D1的面积=(cm2).
14.在主视图和俯视图上标出点A,B,C,D的位置.
略
15.如图是某工件的三视图,求此工件的表面积和体积.
解:由三视图可知,该工件为底面半径为10 cm,高为30 cm的圆锥体.母线长为l=(cm),
S=)π(cm2),
V=×π×(20÷2)2×30=1000 π(cm3).
故此工件的表面积是100(1+)π cm2,体积是1000π cm3.
16.如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处.小明测得窗户距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.
【解析】 如图,连接CD.
∵DO⊥BF,∴∠DOE=90°.
∵OD=0.8 m,OE=0.8 m,
∴∠DEB=45°.
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设AB=BE=x m,
∵AB⊥BF,CO⊥BF,∴AB∥CO,
易得△ABF∽△COF,∴=,
=,解得x=4.4.
答:围墙AB的高度是4.4 m.
