选择性必修第一册3.2双曲线复习 课件(共22张PPT)
文档属性
| 名称 | 选择性必修第一册3.2双曲线复习 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 18:55:33 | ||
图片预览






文档简介
(共22张PPT)
双曲线
双曲线
定义
标准方程
几何性质
直线与双曲线
相交
相切
相离
计算
求弦长
求切线方程
位置关系的判断
焦点在 x轴上
焦点在 y轴上
双曲线定义
第一部分
定义
平面内与两个定点F1,F2的距离__________________等于常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的________ ,两焦点间的距离叫做双曲线的________.
集合P={M| |MF1|–|MF2| =2a},|F1F2|=2c,a>0,c>0.
当2a<|F1F2|时,M点的轨迹为双曲线;
当2a=|F1F2|时,M点的轨迹是两条射线;
当2a>|F1F2|时,M点的轨迹不存在.
F2
F1
O
x
y
M
实轴和虚轴相等的双曲线是等轴双曲线.
离心率为 .
渐近线互相垂直.
之差的绝对值
焦点
焦距
牛刀小试
若双曲线 E: 的左、右焦点分别为F1,F2,点 P在双曲线 E上,且|PF1|=3,则|PF2|等于( )
A. 11
C. 5
B. 9
D. 3
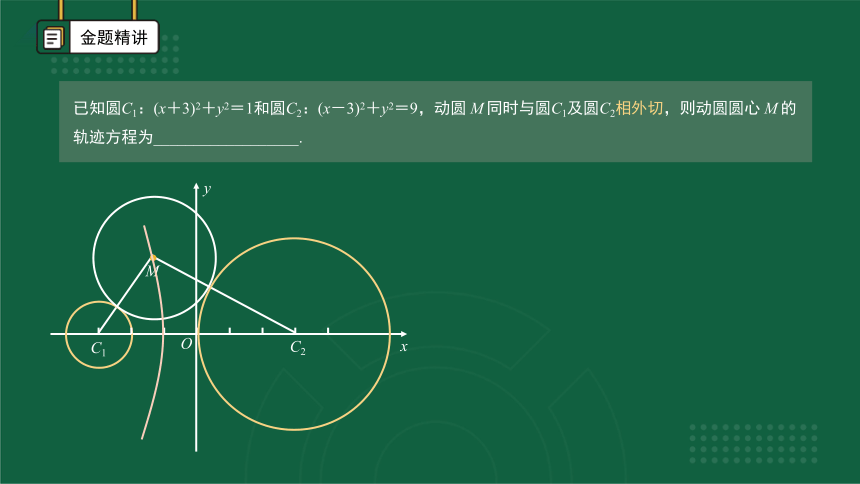
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆 M同时与圆C1及圆C2相外切,则动圆圆心 M的轨迹方程为__________________.
C2
O
x
y
C1
M
应用双曲线定义注意事项
1
2
4
3
距离之差的绝对值,不能漏掉“绝对值”,否则轨迹是一支.
求双曲线方程时,注意标准形式的判断及焦点位置.
2a<|F1|F2|,否则轨迹是射线或不存在.
注意a,b,c的关系(c>a>0,c>b>0).
第二部分
标准方程及性质
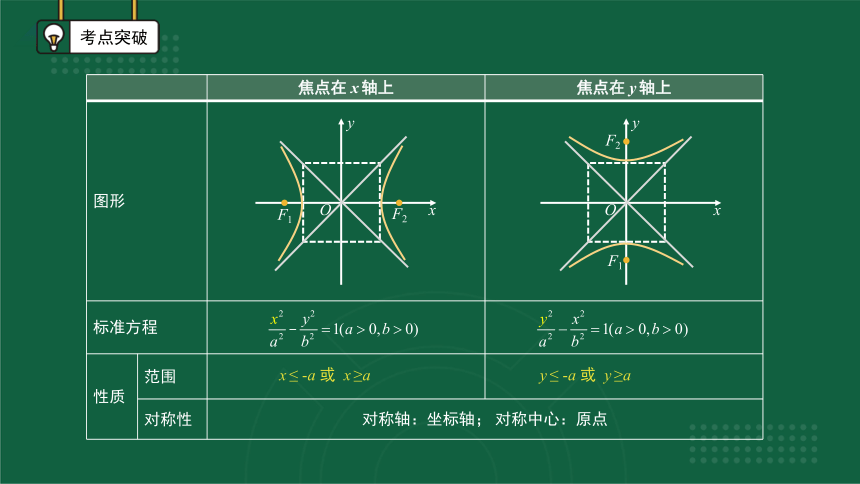
焦点在 x轴上 焦点在 y轴上
图形
标准方程
性质 范围
对称性 对称轴:坐标轴; 对称中心:原点
x≤ -a 或 x≥a
y≤ -a 或 y≥a
F1
F2
x
y
O
F1
F2
x
y
O
焦点在 x轴上 焦点在 y轴上
图形
性质 轴 实轴2a, 虚轴2b
渐近线
离心率
a、b、c关系
c2=a2+b2
F1
F2
x
y
O
F1
F2
x
y
O
知
识
拓
展
1
2
双曲线的焦点到渐近线的距离等于其虚半轴长.
方程的常见设法
与双曲线 共渐近线的方程可设为
若渐近线的方程为 ,则可设双曲线方程为
过双曲线C: 的右顶点作 x轴的垂线,与C的一条渐近线相交于点A. 若以C的右焦点 F为圆心、半径为 4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
A. B. C. D.
F
O
x
y
A
01
求双曲线的方程
方法 解 读 适合题型
定义法 根据定义求 a2 和 b2 ,常用到||PF1|–|PF2||=2a 双曲线上有点到焦点的距离条件
性质法 利用双曲线的性质,如渐近线、焦点等 已知双曲线的某些性质
求双曲线标准方程的方法
02
双曲线的离心率
已知双曲线C: 的左、右焦点分别为F1,F2,过F1的直线与 C的两条渐近线分别交于A,B两点. 若 ,则 C的离心率为________.
F2
O
x
y
F1
A
B
方法 解 读 适合题型
直接法 直接求 a, b,c,利用 适合易求a, b,c
构造法 构造a, b,c间的等式或不等式的奇次关系 可能是a, c或a, b的关系
求离心率的方法
03
双曲线的渐近线
已知双曲线 的左、右焦点分别为F1、F2,过F1作圆 x2+y2=a2 的切线,交双曲线右支于点M,若∠F1MF2=45°,则双曲线的渐近线方程为( )
A.
B.
C. y=±x
D. y=±2x
F2
O
x
y
F1
M
01
求双曲线渐近线注意事项
双曲线 的渐近线是令 ,即得两渐近线方程 .
02
求双曲线渐近线方程的关键是求出a,b的关系,要注意的是双曲线的焦点位置.
位置关系
第三部分
位置关系的判断
直线方程与双曲线方程联立,消去 y或 x得到关于 x或 y的方程.
直线与双曲线相交 1个交点(一次方程)或2个交点( >0)
直线与双曲线相切 1个交点( =0)
直线与双曲线相离 没有交点( <0)
已知双曲线 的左焦点为F1 ,过F1的直线 l交双曲线左支于A, B两点,则直线 l斜率的取值范围为( )
A.
B.
C.
D.
F2
O
x
y
F1
A
B
双曲线
定义
标准方程
几何性质
直线与双曲线
相交
相切
相离
{M|||MF1|–|MF2||=2a(2a<|F1F2|)
求动点轨迹方程
求双曲线方程中2a的值
mx2+ny2=1(mn<0)
与双曲线 共渐近线方程可设为
再见
双曲线
双曲线
定义
标准方程
几何性质
直线与双曲线
相交
相切
相离
计算
求弦长
求切线方程
位置关系的判断
焦点在 x轴上
焦点在 y轴上
双曲线定义
第一部分
定义
平面内与两个定点F1,F2的距离__________________等于常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的________ ,两焦点间的距离叫做双曲线的________.
集合P={M| |MF1|–|MF2| =2a},|F1F2|=2c,a>0,c>0.
当2a<|F1F2|时,M点的轨迹为双曲线;
当2a=|F1F2|时,M点的轨迹是两条射线;
当2a>|F1F2|时,M点的轨迹不存在.
F2
F1
O
x
y
M
实轴和虚轴相等的双曲线是等轴双曲线.
离心率为 .
渐近线互相垂直.
之差的绝对值
焦点
焦距
牛刀小试
若双曲线 E: 的左、右焦点分别为F1,F2,点 P在双曲线 E上,且|PF1|=3,则|PF2|等于( )
A. 11
C. 5
B. 9
D. 3
已知圆C1:(x+3)2+y2=1和圆C2:(x-3)2+y2=9,动圆 M同时与圆C1及圆C2相外切,则动圆圆心 M的轨迹方程为__________________.
C2
O
x
y
C1
M
应用双曲线定义注意事项
1
2
4
3
距离之差的绝对值,不能漏掉“绝对值”,否则轨迹是一支.
求双曲线方程时,注意标准形式的判断及焦点位置.
2a<|F1|F2|,否则轨迹是射线或不存在.
注意a,b,c的关系(c>a>0,c>b>0).
第二部分
标准方程及性质
焦点在 x轴上 焦点在 y轴上
图形
标准方程
性质 范围
对称性 对称轴:坐标轴; 对称中心:原点
x≤ -a 或 x≥a
y≤ -a 或 y≥a
F1
F2
x
y
O
F1
F2
x
y
O
焦点在 x轴上 焦点在 y轴上
图形
性质 轴 实轴2a, 虚轴2b
渐近线
离心率
a、b、c关系
c2=a2+b2
F1
F2
x
y
O
F1
F2
x
y
O
知
识
拓
展
1
2
双曲线的焦点到渐近线的距离等于其虚半轴长.
方程的常见设法
与双曲线 共渐近线的方程可设为
若渐近线的方程为 ,则可设双曲线方程为
过双曲线C: 的右顶点作 x轴的垂线,与C的一条渐近线相交于点A. 若以C的右焦点 F为圆心、半径为 4的圆经过A,O两点(O为坐标原点),则双曲线C的方程为( )
A. B. C. D.
F
O
x
y
A
01
求双曲线的方程
方法 解 读 适合题型
定义法 根据定义求 a2 和 b2 ,常用到||PF1|–|PF2||=2a 双曲线上有点到焦点的距离条件
性质法 利用双曲线的性质,如渐近线、焦点等 已知双曲线的某些性质
求双曲线标准方程的方法
02
双曲线的离心率
已知双曲线C: 的左、右焦点分别为F1,F2,过F1的直线与 C的两条渐近线分别交于A,B两点. 若 ,则 C的离心率为________.
F2
O
x
y
F1
A
B
方法 解 读 适合题型
直接法 直接求 a, b,c,利用 适合易求a, b,c
构造法 构造a, b,c间的等式或不等式的奇次关系 可能是a, c或a, b的关系
求离心率的方法
03
双曲线的渐近线
已知双曲线 的左、右焦点分别为F1、F2,过F1作圆 x2+y2=a2 的切线,交双曲线右支于点M,若∠F1MF2=45°,则双曲线的渐近线方程为( )
A.
B.
C. y=±x
D. y=±2x
F2
O
x
y
F1
M
01
求双曲线渐近线注意事项
双曲线 的渐近线是令 ,即得两渐近线方程 .
02
求双曲线渐近线方程的关键是求出a,b的关系,要注意的是双曲线的焦点位置.
位置关系
第三部分
位置关系的判断
直线方程与双曲线方程联立,消去 y或 x得到关于 x或 y的方程.
直线与双曲线相交 1个交点(一次方程)或2个交点( >0)
直线与双曲线相切 1个交点( =0)
直线与双曲线相离 没有交点( <0)
已知双曲线 的左焦点为F1 ,过F1的直线 l交双曲线左支于A, B两点,则直线 l斜率的取值范围为( )
A.
B.
C.
D.
F2
O
x
y
F1
A
B
双曲线
定义
标准方程
几何性质
直线与双曲线
相交
相切
相离
{M|||MF1|–|MF2||=2a(2a<|F1F2|)
求动点轨迹方程
求双曲线方程中2a的值
mx2+ny2=1(mn<0)
与双曲线 共渐近线方程可设为
再见
