选择性必修第一册3.3抛物线 复习 课件(共22张PPT)
文档属性
| 名称 | 选择性必修第一册3.3抛物线 复习 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-25 18:58:10 | ||
图片预览








文档简介
(共22张PPT)
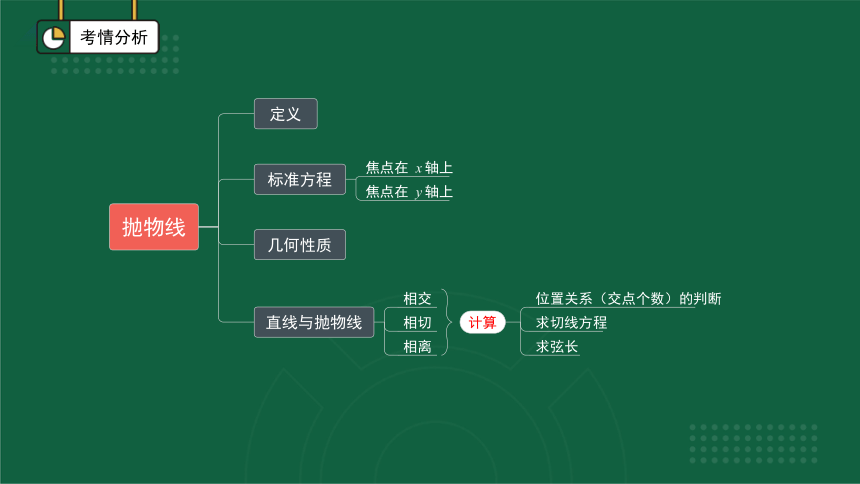
抛物线
抛物线
定义
标准方程
几何性质
直线与抛物线
相交
相切
相离
计算
求弦长
求切线方程
位置关系(交点个数)的判断
焦点在 x轴上
焦点在 y轴上
抛物线定义
第一部分
定义
平面上到定点 F和到定直线 l(l不经过点F)距离_______的点的轨迹叫做抛物线.这个定点叫做抛物线的________ ,直线 l叫做抛物线的________.
集合P={M| |MF| =d}.
当F l时,M点的轨迹为抛物线;
当F∈l时,M点的轨迹是过点F且垂直于直线l的一条直线.
F
O
x
y
M
相等
焦点
准线
牛刀小试
若动点 P与定点F(1,1)和直线 l: 2x–y– 1=0的距离相等,则动点 P的轨迹是( )
A. 椭圆
C. 抛物线
B. 双曲线
D. 直线
F(1,1)
O
x
y
(1)已知 A为抛物线C:y2=2px(p>0)上一点,点 A到 C的焦点的距离为12,到 y轴的距离为9,则p=( )
A. 12
B. 3
C. 6
D. 9
F
O
x
y
A
(2)设 P是抛物线 y2=4x上的一个动点,若B(3,2),则|PB|+|PF|的最小值为________.
F
O
x
y
P
B(3, 2)
M
N
P′
利用抛物线定义可解决的常见问题
01
02
轨迹问题
用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线.
距离问题
涉及抛物线上的点到焦点的距离和到准线的距离问题时,可以利用定义进行相互转化.
第二部分
标准方程及性质
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
p 的几何意义:焦点 F 到准线 l的距离
图形
顶点 O(0,0)
对称轴 x 轴 y 轴
F
O
x
y
F
O
x
y
F
O
x
y
F
O
x
y
图形
焦点
离心率 e=1
准线方程
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
焦半径(其中P(x0,y0))
F
O
x
y
F
O
x
y
F
O
x
y
F
O
x
y
P
知
识
拓
展
F
O
x
y
A(x1, y1)
B(x2, y2)
01
02
03
通径:过焦点垂直于对称轴的弦,长等于2p.
《九章算术》是我国古代内容极为丰富的数学名著,第九章“勾股”,讲述了“勾股定理”及一些应用,直角三角形的三条边长分别称为“勾”“股”“弦”.设点 F是抛物线 y2=2px(p>0)的焦点,l是该抛物线的准线,过抛物线上一点 A作准线的垂线,垂足为B,直线AF交准线 l于点C,若Rt△ABC的“勾”|AB|=3、“股”|CB|= ,则抛物线的方程为( )
A. y2=2x B. y2=3x C. y2=4x D. y2=6x
F
O
x
y
A
B
C
抛物线方程及性质应用注意事项
求抛物线的标准方程的方法及流程
方法:待定系数法
流程:先定位,再定量
应用抛物线性质的关键与技巧
关键:将抛物线方程化成标准方程.
技巧:要结合图形分析,灵活运用平面几何的性质以图助解.
01
02
位置关系
第三部分
位置关系的判断
直线方程与抛物线方程联立,消去 y或 x得到关于 x或 y的方程.
直线与抛物线相交 1个交点(一次方程)或2个交点( >0)
直线与抛物线相切 1个交点( =0)
直线与抛物线相离 没有交点( <0)
已知动点 M到定点F(1,0)的距离比M到定直线x=-2的距离小1.
(1)求点 M的轨迹 C的方程;
F
O
x
y
M
x=-2
(2)过点 F任意作互相垂直的两条直线l1,l2,分别交曲线C于点A,B和M,N.设线段AB,MN的中点分别为P,Q,求证:直线PQ恒过一个定点;
F
O
x
y
M
N
A
B
P
Q
(3)在(2)的条件下,求△FPQ面积的最小值.
F
O
x
y
M
N
A
B
P
Q
解决直线与抛物线问题常用方法与技巧
直线和抛物线的位置关系问题,一般转化为直线方程与抛物线方程组成的方程组问题,利用根与系数的关系或求根公式处理.
涉及弦长的问题时,应熟练地利用根与系数关系,设而不求计算弦长;
涉及垂直关系时也往往利用根与系数关系、设而不求简化运算;
涉及过焦点的弦的问题,可考虑用抛物线的定义求解;
涉及中点弦问题往往利用点差法.涉及到焦点法,用抛物线定义进行转化.
|MF|=d(F l)
定义法
待定系数法
抛物线
定义
标准方程
几何性质
直线与抛物线
相交
相切
相离
计算
求弦长
求切线方程
位置关系(交点个数)的判断
焦点在 x轴上
焦点在 y轴上
再见
抛物线
抛物线
定义
标准方程
几何性质
直线与抛物线
相交
相切
相离
计算
求弦长
求切线方程
位置关系(交点个数)的判断
焦点在 x轴上
焦点在 y轴上
抛物线定义
第一部分
定义
平面上到定点 F和到定直线 l(l不经过点F)距离_______的点的轨迹叫做抛物线.这个定点叫做抛物线的________ ,直线 l叫做抛物线的________.
集合P={M| |MF| =d}.
当F l时,M点的轨迹为抛物线;
当F∈l时,M点的轨迹是过点F且垂直于直线l的一条直线.
F
O
x
y
M
相等
焦点
准线
牛刀小试
若动点 P与定点F(1,1)和直线 l: 2x–y– 1=0的距离相等,则动点 P的轨迹是( )
A. 椭圆
C. 抛物线
B. 双曲线
D. 直线
F(1,1)
O
x
y
(1)已知 A为抛物线C:y2=2px(p>0)上一点,点 A到 C的焦点的距离为12,到 y轴的距离为9,则p=( )
A. 12
B. 3
C. 6
D. 9
F
O
x
y
A
(2)设 P是抛物线 y2=4x上的一个动点,若B(3,2),则|PB|+|PF|的最小值为________.
F
O
x
y
P
B(3, 2)
M
N
P′
利用抛物线定义可解决的常见问题
01
02
轨迹问题
用抛物线的定义可以确定动点与定点、定直线距离有关的轨迹是否为抛物线.
距离问题
涉及抛物线上的点到焦点的距离和到准线的距离问题时,可以利用定义进行相互转化.
第二部分
标准方程及性质
标准方程 y2=2px(p>0) y2=-2px(p>0) x2=2py(p>0) x2=-2py(p>0)
p 的几何意义:焦点 F 到准线 l的距离
图形
顶点 O(0,0)
对称轴 x 轴 y 轴
F
O
x
y
F
O
x
y
F
O
x
y
F
O
x
y
图形
焦点
离心率 e=1
准线方程
范围 x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R
焦半径(其中P(x0,y0))
F
O
x
y
F
O
x
y
F
O
x
y
F
O
x
y
P
知
识
拓
展
F
O
x
y
A(x1, y1)
B(x2, y2)
01
02
03
通径:过焦点垂直于对称轴的弦,长等于2p.
《九章算术》是我国古代内容极为丰富的数学名著,第九章“勾股”,讲述了“勾股定理”及一些应用,直角三角形的三条边长分别称为“勾”“股”“弦”.设点 F是抛物线 y2=2px(p>0)的焦点,l是该抛物线的准线,过抛物线上一点 A作准线的垂线,垂足为B,直线AF交准线 l于点C,若Rt△ABC的“勾”|AB|=3、“股”|CB|= ,则抛物线的方程为( )
A. y2=2x B. y2=3x C. y2=4x D. y2=6x
F
O
x
y
A
B
C
抛物线方程及性质应用注意事项
求抛物线的标准方程的方法及流程
方法:待定系数法
流程:先定位,再定量
应用抛物线性质的关键与技巧
关键:将抛物线方程化成标准方程.
技巧:要结合图形分析,灵活运用平面几何的性质以图助解.
01
02
位置关系
第三部分
位置关系的判断
直线方程与抛物线方程联立,消去 y或 x得到关于 x或 y的方程.
直线与抛物线相交 1个交点(一次方程)或2个交点( >0)
直线与抛物线相切 1个交点( =0)
直线与抛物线相离 没有交点( <0)
已知动点 M到定点F(1,0)的距离比M到定直线x=-2的距离小1.
(1)求点 M的轨迹 C的方程;
F
O
x
y
M
x=-2
(2)过点 F任意作互相垂直的两条直线l1,l2,分别交曲线C于点A,B和M,N.设线段AB,MN的中点分别为P,Q,求证:直线PQ恒过一个定点;
F
O
x
y
M
N
A
B
P
Q
(3)在(2)的条件下,求△FPQ面积的最小值.
F
O
x
y
M
N
A
B
P
Q
解决直线与抛物线问题常用方法与技巧
直线和抛物线的位置关系问题,一般转化为直线方程与抛物线方程组成的方程组问题,利用根与系数的关系或求根公式处理.
涉及弦长的问题时,应熟练地利用根与系数关系,设而不求计算弦长;
涉及垂直关系时也往往利用根与系数关系、设而不求简化运算;
涉及过焦点的弦的问题,可考虑用抛物线的定义求解;
涉及中点弦问题往往利用点差法.涉及到焦点法,用抛物线定义进行转化.
|MF|=d(F l)
定义法
待定系数法
抛物线
定义
标准方程
几何性质
直线与抛物线
相交
相切
相离
计算
求弦长
求切线方程
位置关系(交点个数)的判断
焦点在 x轴上
焦点在 y轴上
再见
