北师大版九年级数学上册1.2矩形的性质与判定(第2课时)教学设计
文档属性
| 名称 | 北师大版九年级数学上册1.2矩形的性质与判定(第2课时)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 42.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 06:07:42 | ||
图片预览

文档简介
第一章 特殊平行四边形
2. 矩形的性质与判定(第2课时)
一、教学目标:
1.探索并证明矩形的判定定理;
2.经历探索、猜测、证明的过程,发展学生的推理论证能力,培养学生找到解题思路的能力,使学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.学生通过对比前面所学知识,体会证明过程中所运用的归纳、概括以及转化等数学思想方法;
4.让学生体会数学是严谨的科学,增强学生对待科学的严谨治学态度,从而养成良好的习惯。
二、教学重难点
重点:探索并证明矩形的判定定理
难点:探索矩形的判定条件并合理利用它进行证明和应用
三、教学过程
(一)以旧引新
1.同学们,在以前的学习中,我们已分别学行四边形、菱形的知识。那么,在学习以上知识版块的时候,我们最主要的是分别从哪几个方面来学习呢?
2.回顾上节课学习的矩形的定义以及性质,引出本课课题。
(二)根据前面所学行四边形、菱形等明确矩形的定义可以作为矩形的一个判定。
(三)由性质定理“矩形的四个角都是直角.”写出逆命题并证明,最后用数学语言表示。
矩形的性质:矩形的四个角都是直角.
逆命题:四个角都是直角的四边形是矩形
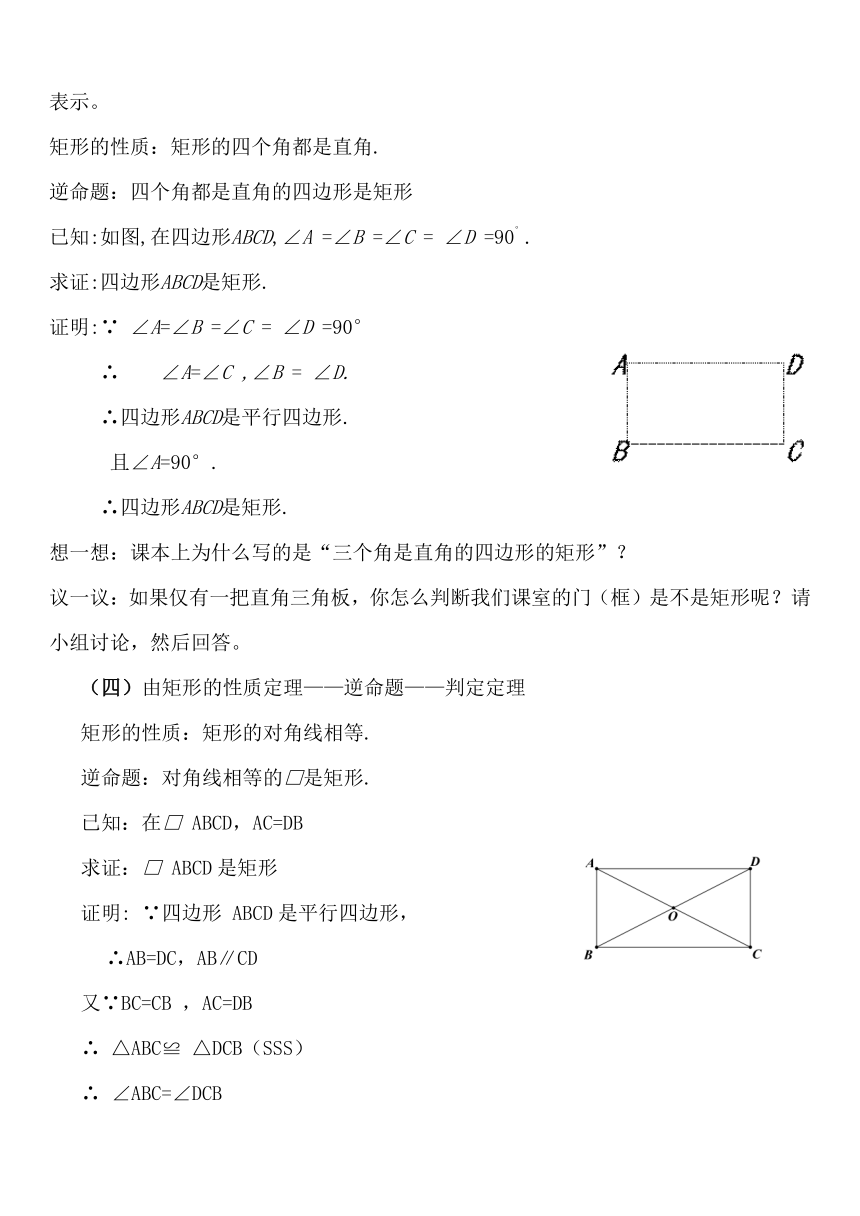
已知:如图,在四边形ABCD,∠A =∠B =∠C = ∠D =90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B =∠C = ∠D =90°
∴ ∠A=∠C ,∠B = ∠D.
∴四边形ABCD是平行四边形.
且∠A=90°.
∴四边形ABCD是矩形.
想一想:课本上为什么写的是“三个角是直角的四边形的矩形”?
议一议:如果仅有一把直角三角板,你怎么判断我们课室的门(框)是不是矩形呢?请小组讨论,然后回答。
(四)由矩形的性质定理——逆命题——判定定理
矩形的性质:矩形的对角线相等.
逆命题:对角线相等的□是矩形.
已知:在□ ABCD,AC=DB
求证:□ ABCD是矩形
证明: ∵四边形 ABCD是平行四边形,
∴AB=DC,AB∥CD
又∵BC=CB ,AC=DB
∴ △ABC≌ △DCB(SSS)
∴ ∠ABC=∠DCB
又∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
板书: 矩形的判定方法3
对角线相等的□是矩形.(并结合图形用数学语言表示)
议一议:还是如何判断我们课室的门(框)是不是矩形?现在的条件是改为如果仅有一根较长的绳子,又该如何来做呢?请讨论,然后回答。
(五)例2:如图在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4. 求□ABCD的面积.
(六)已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
(七)判断对错
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形; ( )
(3)四个角都是直角的四边形是矩形。( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线互相平分且相等的四边形是矩形( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
(八)小结与思考
本节课我们学习了什么内容,你能小结一下吗?
(九)作业布置
课本P16
第1题(基础题)
第2题(拓展题)
四、板书设计(略)
2. 矩形的性质与判定(第2课时)
一、教学目标:
1.探索并证明矩形的判定定理;
2.经历探索、猜测、证明的过程,发展学生的推理论证能力,培养学生找到解题思路的能力,使学生进一步体会证明的必要性以及计算与证明在解决问题中的作用;
3.学生通过对比前面所学知识,体会证明过程中所运用的归纳、概括以及转化等数学思想方法;
4.让学生体会数学是严谨的科学,增强学生对待科学的严谨治学态度,从而养成良好的习惯。
二、教学重难点
重点:探索并证明矩形的判定定理
难点:探索矩形的判定条件并合理利用它进行证明和应用
三、教学过程
(一)以旧引新
1.同学们,在以前的学习中,我们已分别学行四边形、菱形的知识。那么,在学习以上知识版块的时候,我们最主要的是分别从哪几个方面来学习呢?
2.回顾上节课学习的矩形的定义以及性质,引出本课课题。
(二)根据前面所学行四边形、菱形等明确矩形的定义可以作为矩形的一个判定。
(三)由性质定理“矩形的四个角都是直角.”写出逆命题并证明,最后用数学语言表示。
矩形的性质:矩形的四个角都是直角.
逆命题:四个角都是直角的四边形是矩形
已知:如图,在四边形ABCD,∠A =∠B =∠C = ∠D =90°.
求证:四边形ABCD是矩形.
证明:∵ ∠A=∠B =∠C = ∠D =90°
∴ ∠A=∠C ,∠B = ∠D.
∴四边形ABCD是平行四边形.
且∠A=90°.
∴四边形ABCD是矩形.
想一想:课本上为什么写的是“三个角是直角的四边形的矩形”?
议一议:如果仅有一把直角三角板,你怎么判断我们课室的门(框)是不是矩形呢?请小组讨论,然后回答。
(四)由矩形的性质定理——逆命题——判定定理
矩形的性质:矩形的对角线相等.
逆命题:对角线相等的□是矩形.
已知:在□ ABCD,AC=DB
求证:□ ABCD是矩形
证明: ∵四边形 ABCD是平行四边形,
∴AB=DC,AB∥CD
又∵BC=CB ,AC=DB
∴ △ABC≌ △DCB(SSS)
∴ ∠ABC=∠DCB
又∵ AB//CD
∴ ∠ABC+∠DCB=180°
∴ ∠ABC=∠DCB=90°
又∵ 四边形ABCD是平行四边形
∴ □ ABCD是矩形
板书: 矩形的判定方法3
对角线相等的□是矩形.(并结合图形用数学语言表示)
议一议:还是如何判断我们课室的门(框)是不是矩形?现在的条件是改为如果仅有一根较长的绳子,又该如何来做呢?请讨论,然后回答。
(五)例2:如图在□ABCD中,对角线AC和BD相交于点O,△ABO是等边三角形,AB=4. 求□ABCD的面积.
(六)已知:如图,M为平行四边形ABCD边AD的中点,且MB=MC.
求证:四边形ABCD是矩形.
(七)判断对错
(1)有一个角是直角的四边形是矩形;( )
(2)四个角都相等的四边形是矩形; ( )
(3)四个角都是直角的四边形是矩形。( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线互相平分且相等的四边形是矩形( )
(6)两组对边分别平行,且对角线相等的四边形是矩形. ( )
(八)小结与思考
本节课我们学习了什么内容,你能小结一下吗?
(九)作业布置
课本P16
第1题(基础题)
第2题(拓展题)
四、板书设计(略)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
