北师大版八年级数学下册5.1认识分式教学设计
文档属性
| 名称 | 北师大版八年级数学下册5.1认识分式教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 06:58:39 | ||
图片预览



文档简介
认识分式教学设计
一、概述
我讲的是北师大版八年级下册第五章《分式与分式方程》第一节《认识分式》的第一课时。
本节共二个课时,它分为分式的概念,分式的基本性质以及约分,其中分式的基本性质是整章的中心与灵魂,是整章的重点,可类比小学所学过的分数的基本性质来理解分式的基本性质。在学习分式概念时,避免传统教学中对于概念直接给出,叫学生死记硬背,忽略了学生学的过程,也不考虑学生是否真正理解,本课时是让学生通过观察、归纳、总结整式与分式的异同,从而得出分式概念。
二、学生知识状况分析
学生的知识技能基础:学生在小学学过分数,其实分式是分数的“代数化”,所以其性质与运算是完全类似的。在前面的学习中学生已经学会用字母表示实际问题中的数量关系,其中包括整式与分式等数量关系。
学生的活动经验基础:在整式的学习中,学生初步具备了用整式表示现实情境中的数量关系,建立数学模型的思想。在相关的学习中学生初步具备了观察、归纳、类比、猜想的能力以及自主探索、合作交流的能力。
三、教学任务分析
本节课是分式的起始课,是学生学习了整式、因式分解基础上进行的的,是下一步学习分式的性质、分式的运算以及分式方程的前提,所以分式的概念及分式在什么条件下有意义是本节课的重点和难点。因为分式与分数类似,所以为了突破重点和难点,采用了类比的学习方法,让学生学会自主探索,合作交流,老师的讲和学生的学相结合。分式是表示现实世界中一类量的数学模型,为了让学生体会这一点,在课题引入时从学生已掌握的实际知识出发,让学生经历分式概念的形成的过程。根据三维教学目标及新课程标准对本节课的要求,结合当前学生的心理特点以及现有的认知水平,拟定本课的。
四、教学目标:
1、知识与技能:
(1)了解分式的概念,明确分式和整式的区别;
(2)体会分式的意义,进一步发展符号感。
2、过程与方法:
(1)让学生经历用字母表示实际问题中数量关系的过程,体会分式是表示现实世界中的一类量的数学模型;
(2)培养学生观察、归纳、类比的思维,让学生学会自主探索,合作交流。
3、情感与态度:
(1)培养学生相互合作,互帮互助的精神,了解国情,关心社会的意识;
(2)在土地沙化问题中,体会保护人类生存环境的重要性。
五、教学重点、难点及解决重、难点的方法
1、教学重点
分式的概念及分式在什么条件下有意义。
2、教学难点
理解分式概念中的一个特点:分母中含有字母;一个要求:字母的取值限制于使分母的值不得为0。
3、解决重点、难点的方法
教学的关键就是教会学生克服难点,我的办法是从学生较熟悉的小学分数的表示入手类比的学习方法。同时让学生积极参与数学活动探究讨论,再通过进一步归纳,理解概念,达成学习重点的掌握。
六、教学媒体准备
教具:教材
学具:教材、练习本、笔。
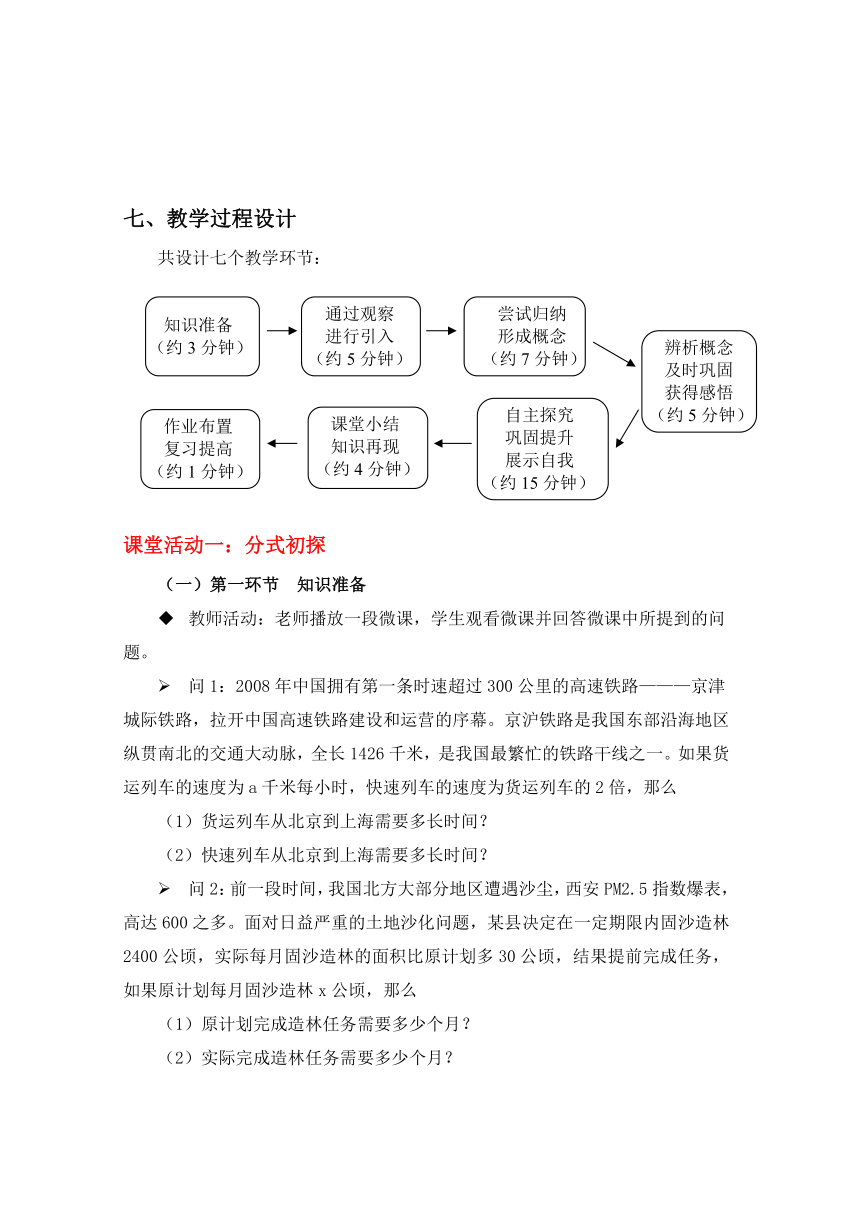
七、教学过程设计
共设计七个教学环节:
课堂活动一:分式初探
(一)第一环节 知识准备
教师活动:老师播放一段微课,学生观看微课并回答微课中所提到的问
题。
问1:2008年中国拥有第一条时速超过300公里的高速铁路———京津
城际铁路,拉开中国高速铁路建设和运营的序幕。京沪铁路是我国东部沿海地区纵贯南北的交通大动脉,全长1426千米,是我国最繁忙的铁路干线之一。如果货运列车的速度为a千米每小时,快速列车的速度为货运列车的2倍,那么
(1)货运列车从北京到上海需要多长时间?
(2)快速列车从北京到上海需要多长时间?
问2:前一段时间,我国北方大部分地区遭遇沙尘,西安PM2.5指数爆表,
高达600之多。面对日益严重的土地沙化问题,某县决定在一定期限内固沙造林2400公顷,实际每月固沙造林的面积比原计划多30公顷,结果提前完成任务,如果原计划每月固沙造林x公顷,那么
(1)原计划完成造林任务需要多少个月?
(2)实际完成造林任务需要多少个月?
问3:用代数式表示
一块长方形的面积是2平方米,长为3米,则宽是_________
一块长方形的面积是S平方米,长为3米,则宽是_________
目的:通过实际问题,让学生初步感受分式是解决问题的一种模型;体会分式的意义,发展符号感。
(二)第二环节 尝试归纳,形成概念(约8分钟)
学生活动:将微课中所得到的六个式子进行分类:
按一定的标准进行分类,并将同一类放在同一个房子,并说明理由。
(有一类是整式 ,其主要特点是分母不含字母;另一类代数式不同于前面学过的整式,暂且称为非整式)在数学上把形如这样的式子称为非整式,引出课题。
教师活动:板书课题 认识分式
小组探究:观察上面非整式有什么特征?
目的:通过讨论,培养学生合作与交流能力。同时归纳其共同特征,从而引出分式的概念。
活动目的:
让学生通过观察、归纳、总结出整式与分式的异同,从而得出分式的概念.
注意事项:
学生通过观察、类比,及小组激烈的讨论,基本能得出分式的定义。老师对定义需要进一步的解释并与分数类比学习的数学思想。对于概念进一步巩固,让学生自己写出分式,小组交流讨论。
形成概念:(类比小学所学的分数) 如果用A、B表示两个整式,A÷B可表
示成 的形式,若B中含有字母,且B≠0,式子 叫做分式。
学生活动二:观察下列代数式,那些是整式,那些是分式?
(三)第三环节 及时巩固, 辨析概念(约5分钟)
例1、下列各式中,哪些是整式?哪些是分式?
(1) (2) (3) (4)
(5) (6) (7)
答:(1)、(2)、(3)、(6)是整式,(4)、(5)、(7)是分式。
学生活动:每人写三个分式,然后小组讨论交流是否是分式。
活动目的:概念进一步的巩固加深,培养学生勤于动脑、勇于探究的精神。同时激发学生的学习兴趣。
教师活动:对学生所写分式进行评价。然后对分式进行几点说明:
1、分式是两个整式相除的商式。
2、分数线有除号和括号的作用。
3、分式与整式最大的不同是分式的分母中含有字母,而整式的分母中不含字母。
活动目的:这样获得的知识,理解的更加透彻,掌握的更加牢固,运用起来会更灵活。
效果:抓住分式与整式的本质特征:分式的分母中有字母。这样以师生互动的方式开始了新课,极大地激发了学生的兴趣,有利于教学活动的展开。
课堂活动二:生成分式
活动内容:教师给出三个整式,不用添加任何运算符号,构造分式。
目的:基于电子白板的功能——移动,让学生自由组合生成分式,使学生在趣味中学习数学,学生对分式概念的理解更加准确、更加深刻。
课堂活动三:分式探究:
探究1: 分式有意义,需要满足:
练习:取何值下列式子有意义?
(1) (2) (3)
注:分式的分母不能为零,而不是分母中的字母不能为零
探究2:分式的值为零,需要满足什么条件?
练习:取何值,分式的值为零?
(1) (2)
探究3:分式值小于零或大于零需要满足什么条件?
练习:为何值分式的值为正?何时值为负?
(1) (2)
注意事项:
对于分式的分母不能为0,有的小组考虑了,有的没有考虑到,就这一点可以让学生类比分数的分母不能为0加以理解,还可理解为字母是可以表示任何数的。这样获得的知识,理解的更加透彻,掌握的更加牢固,运用起来会更灵活。
活动目的:
让学生体会分式的意义,理解如果x的取值使得分母的值为零,则分式没有意义,反之有意义.分式的值等于零、大于零、小于零都与其分子分母有着千丝万缕的联系。通过三个问题的探究,让学生进一步巩固分式相关概念,并学会如何去规范书写。
注意事项:
通过例题讲解,让学生从两方面来理解,一是分式分式中的字母可以表示使分式有意义的任何数;二是分式可与分数类比,分式的分母也不能为零。学生基本能够通过计算出分式的值,但对于分式什么条件下有意义,一下子掌握还有一定的难度, 需要通过与分数进行类比,多举例才能理解的更深刻。
课堂活动四:加强联系 理清结构
改写下列式子
(1)
(2)
(3)
(4)
活动目的:让学生寻找分式的源头,加强知识的联系,加深对分式概念的理解。让学生体会到分式不是什么新鲜与陌生的知识,而是之前已经学过的整式除法而。
课堂活动五:分式练习
1、在下面四个代数式中,分式为( )
A. B. C. D.
2、当x=-1时,下列分式没有意义的是( )
A. B. C. D.
3、当x 时,分式 有意义。
4、当x 时,分式 的值为零。
5、已知,当x=5时,分式 的值等于零,则k = 。
6、当x满足 分式 的值为正或负
教师活动:巡视,同时给有困难的学生以指导。
学生活动:独立完成,从而检验对本节课知识的掌握情况。
活动目的:让学生对知识进行巩固和内化。
预备题库:
1、下列各式中,可能取值为零的是( )
A. B. C. D.
2、下列各式中,无论取何值,分式都有意义的是( )
A. B. C. D.
3 、当______时,分式无意义.
4、当_______时,分式的值为零.
5、使分式无意义,x的取值是( )
A.0 B.1 C. D.
6、解答题:已知,取哪些值时:
(1)的值是零; (2)分式无意义.
7、下列分式,当取何值时有意义.
(1); (2).
选做题:
(1)若a,b为实数,,求3a-b的值
(2)当x为何值时,分式的值为1?当x为何值时,分式的值为-1?
课堂活动六 课堂小结
活动内容:
这节课你有哪些收获?
1、学习了分式的概念,掌握了整式与分式的异同。
2、知道当分式的分母不等于零时分式才有意义。
3、在学习新知识时,可把它与所学的旧知识比较,通过观察、类比、归纳它们的异同的方法来学习新知识。
4、分式的值大于零或小于零需要满足什么条件?
活动目的:
让学生畅所欲言,大胆谈自己的收获和感想,鼓励和引导学生发现和挖掘新事物。
教师用一首诗结束总结:
《古朗分式行》
起初不识它,呼作非整式,
陌生又熟悉,相识在初一;
如今再看它,豁然变开朗:
分数线分层,上下整式连。
分母仅数字,再长名不换;
下面有字母,起名叫分式;
分式有意义,分母忌为零;
分式若为零,上零下不零;
分式有正负,类比分数简,
同正异号负,还望记心田!
注意事项:
检查学生这节课的学习情况,是否把握了重难点,对于没有提到的,要给予补充,对于容易出错的,如当分式的分母不等于零时分式才有意义,要给予强调,另外,还要让学生掌握学习新知识的方法,如可把它与所学的旧知识比较,通过观察、类比、归纳它们的异同的方法来学习新知识。
让可能多的学生谈谈自己的收获,只要积极的正确的都要给予肯定,并及时的鼓励。
通过观察
进行引入
(约5分钟)
知识准备
(约3分钟)
尝试归纳
形成概念
(约7分钟)
辨析概念
及时巩固
获得感悟
(约5分钟)
自主探究
巩固提升
展示自我
(约15分钟)
课堂小结
知识再现
(约4分钟)
作业布置
复习提高
(约1分钟)
PAGE
一、概述
我讲的是北师大版八年级下册第五章《分式与分式方程》第一节《认识分式》的第一课时。
本节共二个课时,它分为分式的概念,分式的基本性质以及约分,其中分式的基本性质是整章的中心与灵魂,是整章的重点,可类比小学所学过的分数的基本性质来理解分式的基本性质。在学习分式概念时,避免传统教学中对于概念直接给出,叫学生死记硬背,忽略了学生学的过程,也不考虑学生是否真正理解,本课时是让学生通过观察、归纳、总结整式与分式的异同,从而得出分式概念。
二、学生知识状况分析
学生的知识技能基础:学生在小学学过分数,其实分式是分数的“代数化”,所以其性质与运算是完全类似的。在前面的学习中学生已经学会用字母表示实际问题中的数量关系,其中包括整式与分式等数量关系。
学生的活动经验基础:在整式的学习中,学生初步具备了用整式表示现实情境中的数量关系,建立数学模型的思想。在相关的学习中学生初步具备了观察、归纳、类比、猜想的能力以及自主探索、合作交流的能力。
三、教学任务分析
本节课是分式的起始课,是学生学习了整式、因式分解基础上进行的的,是下一步学习分式的性质、分式的运算以及分式方程的前提,所以分式的概念及分式在什么条件下有意义是本节课的重点和难点。因为分式与分数类似,所以为了突破重点和难点,采用了类比的学习方法,让学生学会自主探索,合作交流,老师的讲和学生的学相结合。分式是表示现实世界中一类量的数学模型,为了让学生体会这一点,在课题引入时从学生已掌握的实际知识出发,让学生经历分式概念的形成的过程。根据三维教学目标及新课程标准对本节课的要求,结合当前学生的心理特点以及现有的认知水平,拟定本课的。
四、教学目标:
1、知识与技能:
(1)了解分式的概念,明确分式和整式的区别;
(2)体会分式的意义,进一步发展符号感。
2、过程与方法:
(1)让学生经历用字母表示实际问题中数量关系的过程,体会分式是表示现实世界中的一类量的数学模型;
(2)培养学生观察、归纳、类比的思维,让学生学会自主探索,合作交流。
3、情感与态度:
(1)培养学生相互合作,互帮互助的精神,了解国情,关心社会的意识;
(2)在土地沙化问题中,体会保护人类生存环境的重要性。
五、教学重点、难点及解决重、难点的方法
1、教学重点
分式的概念及分式在什么条件下有意义。
2、教学难点
理解分式概念中的一个特点:分母中含有字母;一个要求:字母的取值限制于使分母的值不得为0。
3、解决重点、难点的方法
教学的关键就是教会学生克服难点,我的办法是从学生较熟悉的小学分数的表示入手类比的学习方法。同时让学生积极参与数学活动探究讨论,再通过进一步归纳,理解概念,达成学习重点的掌握。
六、教学媒体准备
教具:教材
学具:教材、练习本、笔。
七、教学过程设计
共设计七个教学环节:
课堂活动一:分式初探
(一)第一环节 知识准备
教师活动:老师播放一段微课,学生观看微课并回答微课中所提到的问
题。
问1:2008年中国拥有第一条时速超过300公里的高速铁路———京津
城际铁路,拉开中国高速铁路建设和运营的序幕。京沪铁路是我国东部沿海地区纵贯南北的交通大动脉,全长1426千米,是我国最繁忙的铁路干线之一。如果货运列车的速度为a千米每小时,快速列车的速度为货运列车的2倍,那么
(1)货运列车从北京到上海需要多长时间?
(2)快速列车从北京到上海需要多长时间?
问2:前一段时间,我国北方大部分地区遭遇沙尘,西安PM2.5指数爆表,
高达600之多。面对日益严重的土地沙化问题,某县决定在一定期限内固沙造林2400公顷,实际每月固沙造林的面积比原计划多30公顷,结果提前完成任务,如果原计划每月固沙造林x公顷,那么
(1)原计划完成造林任务需要多少个月?
(2)实际完成造林任务需要多少个月?
问3:用代数式表示
一块长方形的面积是2平方米,长为3米,则宽是_________
一块长方形的面积是S平方米,长为3米,则宽是_________
目的:通过实际问题,让学生初步感受分式是解决问题的一种模型;体会分式的意义,发展符号感。
(二)第二环节 尝试归纳,形成概念(约8分钟)
学生活动:将微课中所得到的六个式子进行分类:
按一定的标准进行分类,并将同一类放在同一个房子,并说明理由。
(有一类是整式 ,其主要特点是分母不含字母;另一类代数式不同于前面学过的整式,暂且称为非整式)在数学上把形如这样的式子称为非整式,引出课题。
教师活动:板书课题 认识分式
小组探究:观察上面非整式有什么特征?
目的:通过讨论,培养学生合作与交流能力。同时归纳其共同特征,从而引出分式的概念。
活动目的:
让学生通过观察、归纳、总结出整式与分式的异同,从而得出分式的概念.
注意事项:
学生通过观察、类比,及小组激烈的讨论,基本能得出分式的定义。老师对定义需要进一步的解释并与分数类比学习的数学思想。对于概念进一步巩固,让学生自己写出分式,小组交流讨论。
形成概念:(类比小学所学的分数) 如果用A、B表示两个整式,A÷B可表
示成 的形式,若B中含有字母,且B≠0,式子 叫做分式。
学生活动二:观察下列代数式,那些是整式,那些是分式?
(三)第三环节 及时巩固, 辨析概念(约5分钟)
例1、下列各式中,哪些是整式?哪些是分式?
(1) (2) (3) (4)
(5) (6) (7)
答:(1)、(2)、(3)、(6)是整式,(4)、(5)、(7)是分式。
学生活动:每人写三个分式,然后小组讨论交流是否是分式。
活动目的:概念进一步的巩固加深,培养学生勤于动脑、勇于探究的精神。同时激发学生的学习兴趣。
教师活动:对学生所写分式进行评价。然后对分式进行几点说明:
1、分式是两个整式相除的商式。
2、分数线有除号和括号的作用。
3、分式与整式最大的不同是分式的分母中含有字母,而整式的分母中不含字母。
活动目的:这样获得的知识,理解的更加透彻,掌握的更加牢固,运用起来会更灵活。
效果:抓住分式与整式的本质特征:分式的分母中有字母。这样以师生互动的方式开始了新课,极大地激发了学生的兴趣,有利于教学活动的展开。
课堂活动二:生成分式
活动内容:教师给出三个整式,不用添加任何运算符号,构造分式。
目的:基于电子白板的功能——移动,让学生自由组合生成分式,使学生在趣味中学习数学,学生对分式概念的理解更加准确、更加深刻。
课堂活动三:分式探究:
探究1: 分式有意义,需要满足:
练习:取何值下列式子有意义?
(1) (2) (3)
注:分式的分母不能为零,而不是分母中的字母不能为零
探究2:分式的值为零,需要满足什么条件?
练习:取何值,分式的值为零?
(1) (2)
探究3:分式值小于零或大于零需要满足什么条件?
练习:为何值分式的值为正?何时值为负?
(1) (2)
注意事项:
对于分式的分母不能为0,有的小组考虑了,有的没有考虑到,就这一点可以让学生类比分数的分母不能为0加以理解,还可理解为字母是可以表示任何数的。这样获得的知识,理解的更加透彻,掌握的更加牢固,运用起来会更灵活。
活动目的:
让学生体会分式的意义,理解如果x的取值使得分母的值为零,则分式没有意义,反之有意义.分式的值等于零、大于零、小于零都与其分子分母有着千丝万缕的联系。通过三个问题的探究,让学生进一步巩固分式相关概念,并学会如何去规范书写。
注意事项:
通过例题讲解,让学生从两方面来理解,一是分式分式中的字母可以表示使分式有意义的任何数;二是分式可与分数类比,分式的分母也不能为零。学生基本能够通过计算出分式的值,但对于分式什么条件下有意义,一下子掌握还有一定的难度, 需要通过与分数进行类比,多举例才能理解的更深刻。
课堂活动四:加强联系 理清结构
改写下列式子
(1)
(2)
(3)
(4)
活动目的:让学生寻找分式的源头,加强知识的联系,加深对分式概念的理解。让学生体会到分式不是什么新鲜与陌生的知识,而是之前已经学过的整式除法而。
课堂活动五:分式练习
1、在下面四个代数式中,分式为( )
A. B. C. D.
2、当x=-1时,下列分式没有意义的是( )
A. B. C. D.
3、当x 时,分式 有意义。
4、当x 时,分式 的值为零。
5、已知,当x=5时,分式 的值等于零,则k = 。
6、当x满足 分式 的值为正或负
教师活动:巡视,同时给有困难的学生以指导。
学生活动:独立完成,从而检验对本节课知识的掌握情况。
活动目的:让学生对知识进行巩固和内化。
预备题库:
1、下列各式中,可能取值为零的是( )
A. B. C. D.
2、下列各式中,无论取何值,分式都有意义的是( )
A. B. C. D.
3 、当______时,分式无意义.
4、当_______时,分式的值为零.
5、使分式无意义,x的取值是( )
A.0 B.1 C. D.
6、解答题:已知,取哪些值时:
(1)的值是零; (2)分式无意义.
7、下列分式,当取何值时有意义.
(1); (2).
选做题:
(1)若a,b为实数,,求3a-b的值
(2)当x为何值时,分式的值为1?当x为何值时,分式的值为-1?
课堂活动六 课堂小结
活动内容:
这节课你有哪些收获?
1、学习了分式的概念,掌握了整式与分式的异同。
2、知道当分式的分母不等于零时分式才有意义。
3、在学习新知识时,可把它与所学的旧知识比较,通过观察、类比、归纳它们的异同的方法来学习新知识。
4、分式的值大于零或小于零需要满足什么条件?
活动目的:
让学生畅所欲言,大胆谈自己的收获和感想,鼓励和引导学生发现和挖掘新事物。
教师用一首诗结束总结:
《古朗分式行》
起初不识它,呼作非整式,
陌生又熟悉,相识在初一;
如今再看它,豁然变开朗:
分数线分层,上下整式连。
分母仅数字,再长名不换;
下面有字母,起名叫分式;
分式有意义,分母忌为零;
分式若为零,上零下不零;
分式有正负,类比分数简,
同正异号负,还望记心田!
注意事项:
检查学生这节课的学习情况,是否把握了重难点,对于没有提到的,要给予补充,对于容易出错的,如当分式的分母不等于零时分式才有意义,要给予强调,另外,还要让学生掌握学习新知识的方法,如可把它与所学的旧知识比较,通过观察、类比、归纳它们的异同的方法来学习新知识。
让可能多的学生谈谈自己的收获,只要积极的正确的都要给予肯定,并及时的鼓励。
通过观察
进行引入
(约5分钟)
知识准备
(约3分钟)
尝试归纳
形成概念
(约7分钟)
辨析概念
及时巩固
获得感悟
(约5分钟)
自主探究
巩固提升
展示自我
(约15分钟)
课堂小结
知识再现
(约4分钟)
作业布置
复习提高
(约1分钟)
PAGE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
