北师大版八年级数学下册第六章2. 《平行四边形的判定 》教学设计(表格式)
文档属性
| 名称 | 北师大版八年级数学下册第六章2. 《平行四边形的判定 》教学设计(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-26 16:38:45 | ||
图片预览

文档简介
课 题 平行四边形的判定
学 习目 标 1.熟练掌握平行线的判定公理及定理。2.能对平行线的判定进行灵活运用,并把它们应用于几何证明中。发展逻辑推理能力,逐步掌握规范的推理论证格式。3.通过画图、讨论、推理等活动,渗透化归思想。
重 点难 点 重点:平行线的判定公理及定理。难点:能对平行线的判定进行灵活运用,掌握规范的推理论证格式。
教 法选 择 合作探究法 课 型 新授课
课 前准 备 是否采用多 媒 体 是
教 学时 数 1课 时 教 学时 数 第 3课时 备 课总 数 第 64 课时
课 堂 教 学 过 程 设 计
教学内容 教师活动 学生活动
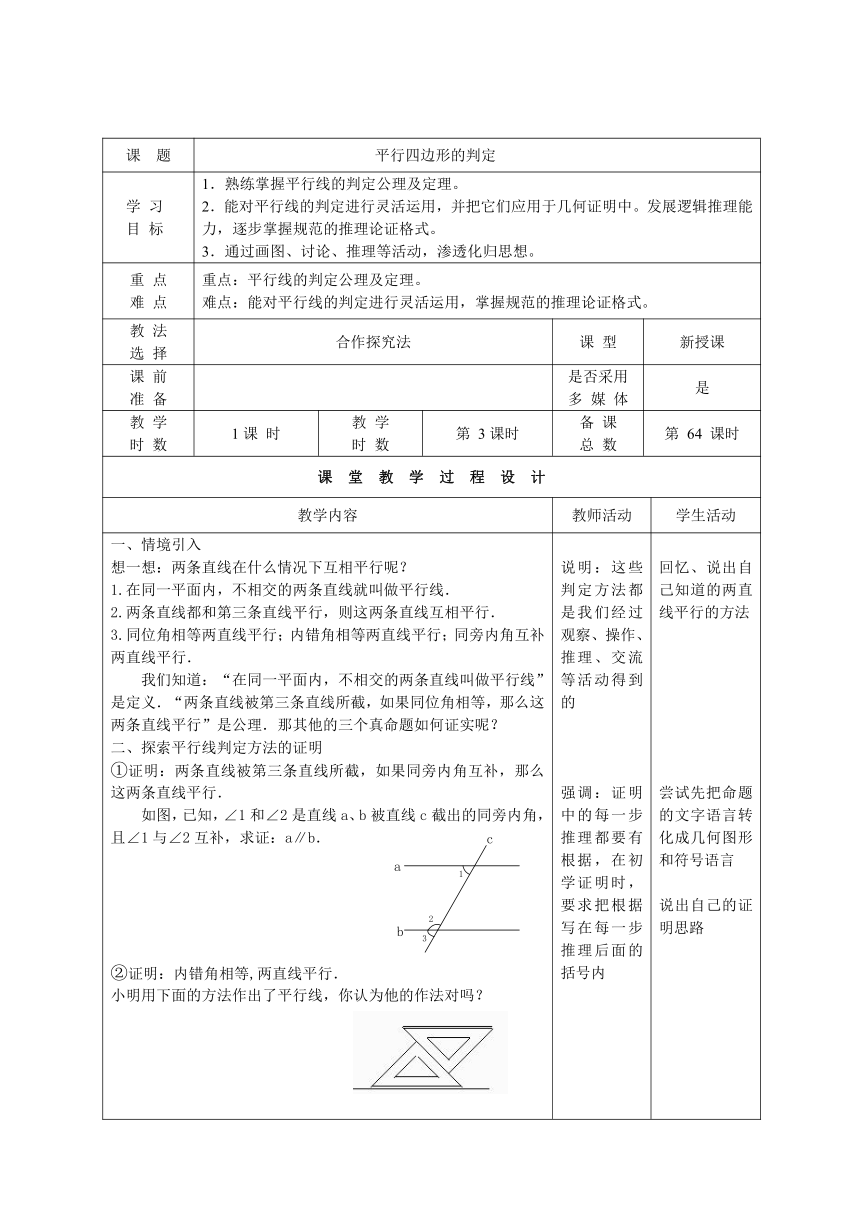
情境引入想一想:两条直线在什么情况下互相平行呢?1.在同一平面内,不相交的两条直线就叫做平行线.2.两条直线都和第三条直线平行,则这两条直线互相平行.3.同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行.我们知道:“在同一平面内,不相交的两条直线叫做平行线”是定义.“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”是公理.那其他的三个真命题如何证实呢?探索平行线判定方法的证明①证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.如图,已知,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补,求证:a∥b.②证明:内错角相等,两直线平行.小明用下面的方法作出了平行线,你认为他的作法对吗? 说明:这些判定方法都是我们经过观察、操作、推理、交流等活动得到的强调:证明中的每一步推理都要有根据,在初学证明时,要求把根据写在每一步推理后面的括号内 回忆、说出自己知道的两直线平行的方法尝试先把命题的文字语言转化成几何图形和符号语言说出自己的证明思路
教学内容 学生活动 教师活动
已知,∠1和∠2是直线a、b被直线c截出的内错角,且∠1=∠2. 求证:a∥b③ 借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论呢?已知,如图,直线a⊥c,b⊥c.求证:a∥b. 结论:“如果两条直线都和第三条直线垂直,那么这两条直线平行”反馈练习蜂房的顶部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=,∠β=.试确定这个四边形对边的位置关系。四、课堂小结 : 要求学生类比上述证明转化成几何图形和符号语言说明:已给的基本事实、定义和已经证明的定理都可以作为依据,用来证明新的结论通过练习,对学生的状况进行分析出示小结点拨提示归纳小结 尝试独立完成结论的证明互相点评与老师共同完成证明逐步掌握规范的推理格式独立完成练习纠正自己的错误谈学习的收获和存在的问题完成小结再次体会
作 业设 置 习题7.4 知识技能1数学理解2
教学反思 等级评价(A/B/C/D)
检查签阅 第 周,应备 课时 实备 课时,共 课时评价: 时间: 签查(盖章):
β
α
学 习目 标 1.熟练掌握平行线的判定公理及定理。2.能对平行线的判定进行灵活运用,并把它们应用于几何证明中。发展逻辑推理能力,逐步掌握规范的推理论证格式。3.通过画图、讨论、推理等活动,渗透化归思想。
重 点难 点 重点:平行线的判定公理及定理。难点:能对平行线的判定进行灵活运用,掌握规范的推理论证格式。
教 法选 择 合作探究法 课 型 新授课
课 前准 备 是否采用多 媒 体 是
教 学时 数 1课 时 教 学时 数 第 3课时 备 课总 数 第 64 课时
课 堂 教 学 过 程 设 计
教学内容 教师活动 学生活动
情境引入想一想:两条直线在什么情况下互相平行呢?1.在同一平面内,不相交的两条直线就叫做平行线.2.两条直线都和第三条直线平行,则这两条直线互相平行.3.同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行.我们知道:“在同一平面内,不相交的两条直线叫做平行线”是定义.“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”是公理.那其他的三个真命题如何证实呢?探索平行线判定方法的证明①证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.如图,已知,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补,求证:a∥b.②证明:内错角相等,两直线平行.小明用下面的方法作出了平行线,你认为他的作法对吗? 说明:这些判定方法都是我们经过观察、操作、推理、交流等活动得到的强调:证明中的每一步推理都要有根据,在初学证明时,要求把根据写在每一步推理后面的括号内 回忆、说出自己知道的两直线平行的方法尝试先把命题的文字语言转化成几何图形和符号语言说出自己的证明思路
教学内容 学生活动 教师活动
已知,∠1和∠2是直线a、b被直线c截出的内错角,且∠1=∠2. 求证:a∥b③ 借助“同位角相等,两直线平行”这一公理,你还能证明哪些熟悉的结论呢?已知,如图,直线a⊥c,b⊥c.求证:a∥b. 结论:“如果两条直线都和第三条直线垂直,那么这两条直线平行”反馈练习蜂房的顶部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=,∠β=.试确定这个四边形对边的位置关系。四、课堂小结 : 要求学生类比上述证明转化成几何图形和符号语言说明:已给的基本事实、定义和已经证明的定理都可以作为依据,用来证明新的结论通过练习,对学生的状况进行分析出示小结点拨提示归纳小结 尝试独立完成结论的证明互相点评与老师共同完成证明逐步掌握规范的推理格式独立完成练习纠正自己的错误谈学习的收获和存在的问题完成小结再次体会
作 业设 置 习题7.4 知识技能1数学理解2
教学反思 等级评价(A/B/C/D)
检查签阅 第 周,应备 课时 实备 课时,共 课时评价: 时间: 签查(盖章):
β
α
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
