北京版七年级数学下册6.3 整式的乘法-多项式与多项式相乘教学设计(表格式)
文档属性
| 名称 | 北京版七年级数学下册6.3 整式的乘法-多项式与多项式相乘教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 53.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-27 07:38:12 | ||
图片预览

文档简介
课题 多项式与多项式相乘 授课教师
课标 能进行简单的整式乘法运算(其中多项式相乘仅指一次式之间以及一次式与二次式相乘)。
教材分析 整式的乘法是整数运算的主要内容,是进一步学习因式分解、分式、方程以及其它数学内容的基础,学习多项式与多项式的乘法既是多项式的加法、单项式与单项式乘法的综合应用,也是学习乘法公式的基础。通过本节课的学习,让学生体验数学与现实生活的联系,经历知识的形成过程,使学生思维的灵活性、广泛性、深刻性上得到进一步发展。多项式乘法是
本章重点内容之一,同时也是前几节各种性质、法则的一个综合运用。学生经过本章前几节知识的学习,和对幂的运算性质、单项式的乘法以及单项式与多项式的乘法的小结、复习具备了学习多项式乘法的基础知识和探究这类知识的基本意识和基本技能。学习过程中只要能理解并运用数学常用方法“整体代入”便可突破教学难点,同时为后继学习方法和能力的提升,打下良好的基础。
学情分析 初一(2)班共33人,优生人数少,10名学生不及格,普遍运算能力较弱,准确率较低,数感较差,部分学生需要老师的帮助和监督才能完成学习任务。学生已经学过幂的运算、单项式的乘法以及单项式与多项式的乘法,但是学习效果不佳,对运算性质掌握不到位,运算准确性不足,容易混淆,所以上课需要理解运算法则的产生过程,掌握探究的方法。
教学目标 知识与技能目标:经历探索多项式乘法法则的过程,理解多项式乘法法则;灵活运用多项式乘以多项式的运算法则。 过程与方法目标:经历探索乘法法则的过程,发展观察、归纳、猜测、验证的能力;体会乘法分配律的作用与转化思想,发展有条理的思考及语言表达能力。 情感与态度目标:体验学习和把握数学问题的方法,树立学好数学的信心,培养学习数学的兴趣。
重点 多项式与多项式相乘的法则及其应用。
难点 探索多项式的乘法法则,灵活地进行整式的乘法运算。 突破方法 类比,分析,启发
教学方式 探究式,小组合作
教学过程
教师活动 学生活动 设计意图
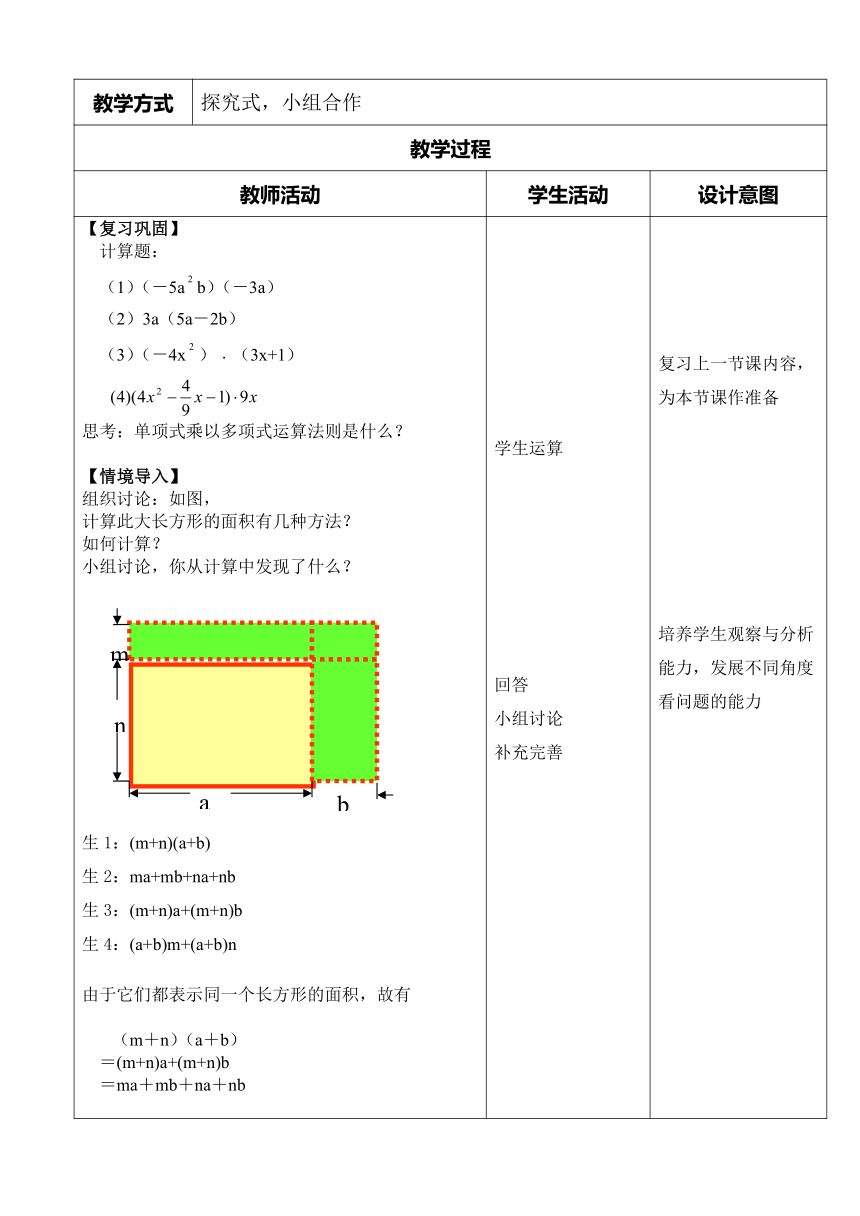
【复习巩固】 计算题: (1)(-5ab)(-3a) (2)3a(5a-2b) (3)(-4x)﹒(3x+1) 思考:单项式乘以多项式运算法则是什么? 【情境导入】 组织讨论:如图, 计算此大长方形的面积有几种方法? 如何计算? 小组讨论,你从计算中发现了什么? 生1:(m+n)(a+b) 生2:ma+mb+na+nb 生3:(m+n)a+(m+n)b 生4:(a+b)m+(a+b)n 由于它们都表示同一个长方形的面积,故有 (m+n)(a+b) =(m+n)a+(m+n)b =ma+mb+na+nb 学生运算 回答 小组讨论 补充完善 复习上一节课内容,为本节课作准备 培养学生观察与分析能力,发展不同角度看问题的能力
【探索法则与应用】 根据乘法分配律,我们也能得到下面等式: (m+n)(a+b)=ma+mb+na+nb 在学生发言的基础上,总结多项式与多项式的乘法法则并板书法则。 让学生体会法则的理论依据:乘法对加法的分配律。 多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。 学生总结多项式与多项式的乘法法则,回答补充 锻炼学生的归纳总结能力
【例题讲解】 例1.计算 (1) (2) 解:(1)(x+2)(x-3) =x﹒x+x﹒(-3)+2﹒x+2﹒(-3) =x2-3x+2x-6 =x2-3x+2x-6 (2) (3x -1)(2x+1) =3x 2x+3x 1-1 2 x-1 =6x2+3x-2x-1 =6x2+x-1 学生认真听讲,思考,计算 培养学生的集中精力听讲的习惯,熟悉计算法则
【巩固练习】 1、计算下列各题 (1) (2x+1)(x+3) (2) (m-2n)(m+3n) (3) (a-1)(a-1) (4) (a+3b)(a-3b) (5) (x+2)(x+3) (6) (x-4)(x+1) (7) (y+4)(y-2) (8) (y-5)(y-3) 【想一想:】 (m+n)(a+b)= (m+n)(a+b+c)= (m+n)(a+b+c)=ma+mb+mc+ na+nb+nc 计算: (1) (x–1)(x2+x+1) ; (2) 注意:一定要用第一个多项式的每一项依次去乘第二个多项式的每一项,在计算时要注意多项式中每个单项式的符号。 【思考交流】 1、多项式与多项式相乘,积的项数与各个因式的项数有什么关系? 2、多项式与多项式相乘,与单项式与多项式相乘有什么相同点和不同点? 【拓展训练】 计算: (1)(x+1)2 (2)(x-2y)2 学生思考,回答,集体订正 思考,联系 (m+n)(a+b) =ma+mb+na+nb 进行拓展,填空 练习,计算,交流 思考,交流,补充 转化 ,练习,纠错 培养学生对知识的应用能力和学习积极性 培养学生猜想归纳和灵活运用的能力。 锻炼学生分析问题,解决问题的能力
【课堂小结】 1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。注意做到不重不漏。 2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。 3、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法,从而使学习能够进行。 学生归纳,补充完善 明确本节要点,进行系统整理,培养学生归纳的能力和习惯,强化知识体系。
课标 能进行简单的整式乘法运算(其中多项式相乘仅指一次式之间以及一次式与二次式相乘)。
教材分析 整式的乘法是整数运算的主要内容,是进一步学习因式分解、分式、方程以及其它数学内容的基础,学习多项式与多项式的乘法既是多项式的加法、单项式与单项式乘法的综合应用,也是学习乘法公式的基础。通过本节课的学习,让学生体验数学与现实生活的联系,经历知识的形成过程,使学生思维的灵活性、广泛性、深刻性上得到进一步发展。多项式乘法是
本章重点内容之一,同时也是前几节各种性质、法则的一个综合运用。学生经过本章前几节知识的学习,和对幂的运算性质、单项式的乘法以及单项式与多项式的乘法的小结、复习具备了学习多项式乘法的基础知识和探究这类知识的基本意识和基本技能。学习过程中只要能理解并运用数学常用方法“整体代入”便可突破教学难点,同时为后继学习方法和能力的提升,打下良好的基础。
学情分析 初一(2)班共33人,优生人数少,10名学生不及格,普遍运算能力较弱,准确率较低,数感较差,部分学生需要老师的帮助和监督才能完成学习任务。学生已经学过幂的运算、单项式的乘法以及单项式与多项式的乘法,但是学习效果不佳,对运算性质掌握不到位,运算准确性不足,容易混淆,所以上课需要理解运算法则的产生过程,掌握探究的方法。
教学目标 知识与技能目标:经历探索多项式乘法法则的过程,理解多项式乘法法则;灵活运用多项式乘以多项式的运算法则。 过程与方法目标:经历探索乘法法则的过程,发展观察、归纳、猜测、验证的能力;体会乘法分配律的作用与转化思想,发展有条理的思考及语言表达能力。 情感与态度目标:体验学习和把握数学问题的方法,树立学好数学的信心,培养学习数学的兴趣。
重点 多项式与多项式相乘的法则及其应用。
难点 探索多项式的乘法法则,灵活地进行整式的乘法运算。 突破方法 类比,分析,启发
教学方式 探究式,小组合作
教学过程
教师活动 学生活动 设计意图
【复习巩固】 计算题: (1)(-5ab)(-3a) (2)3a(5a-2b) (3)(-4x)﹒(3x+1) 思考:单项式乘以多项式运算法则是什么? 【情境导入】 组织讨论:如图, 计算此大长方形的面积有几种方法? 如何计算? 小组讨论,你从计算中发现了什么? 生1:(m+n)(a+b) 生2:ma+mb+na+nb 生3:(m+n)a+(m+n)b 生4:(a+b)m+(a+b)n 由于它们都表示同一个长方形的面积,故有 (m+n)(a+b) =(m+n)a+(m+n)b =ma+mb+na+nb 学生运算 回答 小组讨论 补充完善 复习上一节课内容,为本节课作准备 培养学生观察与分析能力,发展不同角度看问题的能力
【探索法则与应用】 根据乘法分配律,我们也能得到下面等式: (m+n)(a+b)=ma+mb+na+nb 在学生发言的基础上,总结多项式与多项式的乘法法则并板书法则。 让学生体会法则的理论依据:乘法对加法的分配律。 多项式乘以多项式,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。 学生总结多项式与多项式的乘法法则,回答补充 锻炼学生的归纳总结能力
【例题讲解】 例1.计算 (1) (2) 解:(1)(x+2)(x-3) =x﹒x+x﹒(-3)+2﹒x+2﹒(-3) =x2-3x+2x-6 =x2-3x+2x-6 (2) (3x -1)(2x+1) =3x 2x+3x 1-1 2 x-1 =6x2+3x-2x-1 =6x2+x-1 学生认真听讲,思考,计算 培养学生的集中精力听讲的习惯,熟悉计算法则
【巩固练习】 1、计算下列各题 (1) (2x+1)(x+3) (2) (m-2n)(m+3n) (3) (a-1)(a-1) (4) (a+3b)(a-3b) (5) (x+2)(x+3) (6) (x-4)(x+1) (7) (y+4)(y-2) (8) (y-5)(y-3) 【想一想:】 (m+n)(a+b)= (m+n)(a+b+c)= (m+n)(a+b+c)=ma+mb+mc+ na+nb+nc 计算: (1) (x–1)(x2+x+1) ; (2) 注意:一定要用第一个多项式的每一项依次去乘第二个多项式的每一项,在计算时要注意多项式中每个单项式的符号。 【思考交流】 1、多项式与多项式相乘,积的项数与各个因式的项数有什么关系? 2、多项式与多项式相乘,与单项式与多项式相乘有什么相同点和不同点? 【拓展训练】 计算: (1)(x+1)2 (2)(x-2y)2 学生思考,回答,集体订正 思考,联系 (m+n)(a+b) =ma+mb+na+nb 进行拓展,填空 练习,计算,交流 思考,交流,补充 转化 ,练习,纠错 培养学生对知识的应用能力和学习积极性 培养学生猜想归纳和灵活运用的能力。 锻炼学生分析问题,解决问题的能力
【课堂小结】 1、多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。注意做到不重不漏。 2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。 3、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法,从而使学习能够进行。 学生归纳,补充完善 明确本节要点,进行系统整理,培养学生归纳的能力和习惯,强化知识体系。
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
