方程的根与函数的零点教案
图片预览


文档简介
第三章 函数的应用
课题 3.1.1方程的根与函数的零点
教学目标:
知识与技能:理解函数零点的意义,能判断二次函数零点的存在性,会求简单函数的零点,了解零点与方程根的关系,初步形成用函数观点处理问题的意识。
过程与方法:通过体验函数零点的形成过程,零点存在性的探索过程,提高数学知识的综合运用能力,体会数形结合的数学思想,函数与方程,从特殊到一般的归纳思想。
情感态度与价值观:通过函数零点与方程根的联系,体会事物之间相互变化的辨证思想
教学重点:
函数零点与方程根之间的关系,连续函数在某区间上存在零点的判定方法
教学难点:
探究发现函数存在零点的判定方法
教学方法:
问题引领、启发诱导
使用教具:多媒体
学情分析:
学生已有的认知基础是,初中学习过二次函数图象和二次方程,并且解过“当函数值为0时,求相应自变量的值”的问题,初步认识到二次方程与二次函数的联系,对二次函数图象与轴是否相交,也有一些直观的认识与体会。在高中阶段,已经学习了函数概念与性质,掌握了部分基本初等函数的图象与性质。这就为学习本节内容打下了知识基础。
一、导入新课
问题1、求下列方程的根
①②③
第③题学生无法解答,产生疑惑,引出课题
二、新课——方程的根与函数的零点
1、函数零点的概念
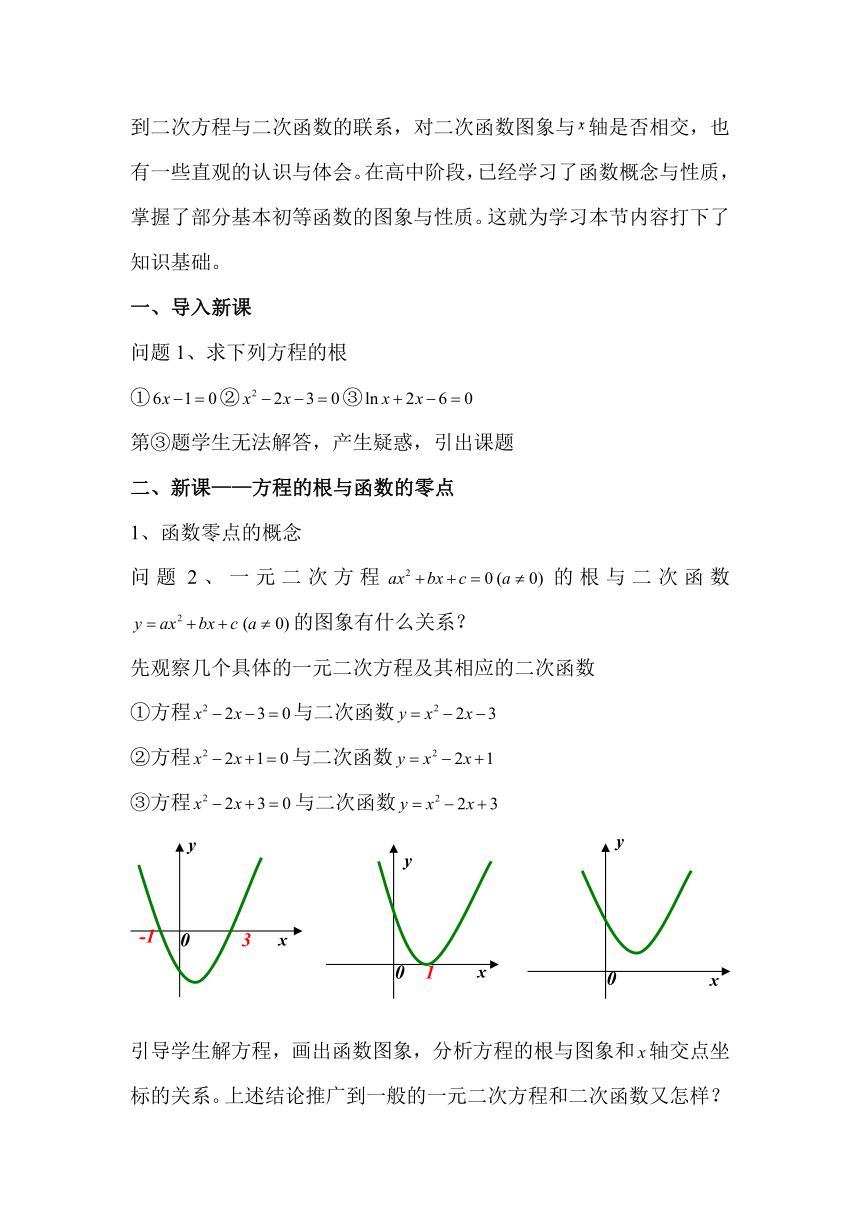
问题2、一元二次方程的根与二次函数的图象有什么关系?
先观察几个具体的一元二次方程及其相应的二次函数
①方程与二次函数
②方程与二次函数
③方程与二次函数
引导学生解方程,画出函数图象,分析方程的根与图象和轴交点坐标的关系。上述结论推广到一般的一元二次方程和二次函数又怎样?推广到一般的方程和函数呢?
填写下表:
函数零点的概念:对于函数,我们把使的实数叫做函数的零点。
2、方程的根与函数零点的关系
问题3、零点是点吗?零点与方程的根有什么关系?零点与函数图象与轴的交点有什么关系?
函数的零点并不是“点”,它不是以坐标的形式出现的,而是实数,例如函数的零点为
函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标。
结论:方程有实数根
函数的图象与轴有交点
函数有零点
3、函数零点的求法
问题4、如何根据函数零点的意义求零点?
①(代数法)求方程的实数根
②(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点
二次函数的零点(看)
当时,方程有两个不等的实数根,函数的图象与轴有两个交点,函数有两个零点;当时,方程有两个相等的实数根,函数的图象与轴有一个交点,函数有一个零点;当时,方程没有实数根,函数的图象与轴没有交点,函数没有零点。
练习:求下列函数的零点
①
②
4、函数零点存在性的判定
函数在某个区间上是否一定有零点?
怎样的条件下,函数一定有零点?
问题5、观察二次函数的图象在区间上是否有零点?计算与的乘积,你能发现这个乘积有什么特点?在区间上呢?
观察函数的图象,能否得出同样的结论?
1 在区间(a,b)内_____(有/无)零点;
f(a)f(b)_____ 0(<或>).
② 在区间(b,c)内______(有/无)零点;
f(b)f(c) _____ 0(<或>).
③ 在区间(c,d)内______(有/无)零点;
f(c)f(d) _____ 0(<或>).
结论:如果函数在区间上的图象是连续不断的一条曲线,并且有,那么,函数在区间内有零点,即存在,使得。这个也就是方程的根。
注意:1、它是判断任意函数的零点存在的方法,只能判断函数零点是否存在,而无法确定零点存在的个数
2、反之不真
例1、 求函数的零点个数
解:此函数定义域为(0,+∞)
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
从列表和图象可看出,f(2)<0 , f(3)>0
即f(2)·f(3)<0,所以函数在(2,3)内
有零点。又由于函数在整个定义域内
是增函数,故只有一个零点。
三、课堂练习:见教材1、2
四、课堂小结:学完本节课,你有哪些收获?
1、函数零点的定义;
2、函数的零点与方程的根的关系;
3、确定函数的零点的方法。
4、思想方法:数形结合思想,函数与方程思想,从特殊到一般的归纳思想。
五、作业:
1. 1、2
2.思考:
函数 的零点在区间上,如何求出这个零点?
板书设计
§3.1.1 方程的根与函数的零点
一、函数的零点的概念二、 三个等价关系三、函数零点的求法四、判定零点的存在性:1 函数是连续的。2 f(a)f(b)<0。3 至少有一个零点。 例…… 练习:(1)……(2)……
多
媒
体
演
示
9
1
2
3
4
6
7
8
14
12
6
8
10
4
2
y
-1
3
0
x
y
0
1
x
y
0
5
10
-6
-4
-2
0
x
y
x
课题 3.1.1方程的根与函数的零点
教学目标:
知识与技能:理解函数零点的意义,能判断二次函数零点的存在性,会求简单函数的零点,了解零点与方程根的关系,初步形成用函数观点处理问题的意识。
过程与方法:通过体验函数零点的形成过程,零点存在性的探索过程,提高数学知识的综合运用能力,体会数形结合的数学思想,函数与方程,从特殊到一般的归纳思想。
情感态度与价值观:通过函数零点与方程根的联系,体会事物之间相互变化的辨证思想
教学重点:
函数零点与方程根之间的关系,连续函数在某区间上存在零点的判定方法
教学难点:
探究发现函数存在零点的判定方法
教学方法:
问题引领、启发诱导
使用教具:多媒体
学情分析:
学生已有的认知基础是,初中学习过二次函数图象和二次方程,并且解过“当函数值为0时,求相应自变量的值”的问题,初步认识到二次方程与二次函数的联系,对二次函数图象与轴是否相交,也有一些直观的认识与体会。在高中阶段,已经学习了函数概念与性质,掌握了部分基本初等函数的图象与性质。这就为学习本节内容打下了知识基础。
一、导入新课
问题1、求下列方程的根
①②③
第③题学生无法解答,产生疑惑,引出课题
二、新课——方程的根与函数的零点
1、函数零点的概念
问题2、一元二次方程的根与二次函数的图象有什么关系?
先观察几个具体的一元二次方程及其相应的二次函数
①方程与二次函数
②方程与二次函数
③方程与二次函数
引导学生解方程,画出函数图象,分析方程的根与图象和轴交点坐标的关系。上述结论推广到一般的一元二次方程和二次函数又怎样?推广到一般的方程和函数呢?
填写下表:
函数零点的概念:对于函数,我们把使的实数叫做函数的零点。
2、方程的根与函数零点的关系
问题3、零点是点吗?零点与方程的根有什么关系?零点与函数图象与轴的交点有什么关系?
函数的零点并不是“点”,它不是以坐标的形式出现的,而是实数,例如函数的零点为
函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标。
结论:方程有实数根
函数的图象与轴有交点
函数有零点
3、函数零点的求法
问题4、如何根据函数零点的意义求零点?
①(代数法)求方程的实数根
②(几何法)对于不能用求根公式的方程,可以将它与函数的图象联系起来,并利用函数的性质找出零点
二次函数的零点(看)
当时,方程有两个不等的实数根,函数的图象与轴有两个交点,函数有两个零点;当时,方程有两个相等的实数根,函数的图象与轴有一个交点,函数有一个零点;当时,方程没有实数根,函数的图象与轴没有交点,函数没有零点。
练习:求下列函数的零点
①
②
4、函数零点存在性的判定
函数在某个区间上是否一定有零点?
怎样的条件下,函数一定有零点?
问题5、观察二次函数的图象在区间上是否有零点?计算与的乘积,你能发现这个乘积有什么特点?在区间上呢?
观察函数的图象,能否得出同样的结论?
1 在区间(a,b)内_____(有/无)零点;
f(a)f(b)_____ 0(<或>).
② 在区间(b,c)内______(有/无)零点;
f(b)f(c) _____ 0(<或>).
③ 在区间(c,d)内______(有/无)零点;
f(c)f(d) _____ 0(<或>).
结论:如果函数在区间上的图象是连续不断的一条曲线,并且有,那么,函数在区间内有零点,即存在,使得。这个也就是方程的根。
注意:1、它是判断任意函数的零点存在的方法,只能判断函数零点是否存在,而无法确定零点存在的个数
2、反之不真
例1、 求函数的零点个数
解:此函数定义域为(0,+∞)
x 1 2 3 4 5 6 7 8 9
f(x) -4 -1.3069 1.0986 3.3863 5.6094 7.7918 9.9459 12.0794 14.1972
从列表和图象可看出,f(2)<0 , f(3)>0
即f(2)·f(3)<0,所以函数在(2,3)内
有零点。又由于函数在整个定义域内
是增函数,故只有一个零点。
三、课堂练习:见教材1、2
四、课堂小结:学完本节课,你有哪些收获?
1、函数零点的定义;
2、函数的零点与方程的根的关系;
3、确定函数的零点的方法。
4、思想方法:数形结合思想,函数与方程思想,从特殊到一般的归纳思想。
五、作业:
1. 1、2
2.思考:
函数 的零点在区间上,如何求出这个零点?
板书设计
§3.1.1 方程的根与函数的零点
一、函数的零点的概念二、 三个等价关系三、函数零点的求法四、判定零点的存在性:1 函数是连续的。2 f(a)f(b)<0。3 至少有一个零点。 例…… 练习:(1)……(2)……
多
媒
体
演
示
9
1
2
3
4
6
7
8
14
12
6
8
10
4
2
y
-1
3
0
x
y
0
1
x
y
0
5
10
-6
-4
-2
0
x
y
x
